10.5: Suspension in a Shear Flow- The Diffusional Theory of Suspension
- Page ID
- 4215
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Suspended particles are held up above the bed by the turbulent motion of the fluid. The weight of the particle is transmitted directly to the fluid, by way of the drag force exerted by the particles as they fall through the surrounding fluid, and increases the hydrostatic fluid pressure at the bed, in much the same way an airplane in flight increases the atmospheric pressure in an ill-defined circular area on the ground below. Suspended particles thus exert a force on the bed, albeit indirectly, in contrast to the direct forces exerted on the bed by moving bed-load particles.
It is theoretically possible for particles to move through the fluid close to the bed without actually being in contact with the bed, and yet not be in suspension. This happens in true saltation: the ballistic motion of the particles results from fluid lift forces and/or particles striking the bed, but it is not at all dependent on turbulence—and in fact Francis (1973) has described saltation of particles in a laminar flow. It has also been postulated that particles may be held in a dispersed state close to the bed by actual collisions between particles or by near-misses that produce viscous forces with vertical components that hold the particles above the bed. This is the “dispersive pressure” of Bagnold (1956), the effectiveness of which is still a matter for debate.
It was noted earlier in this chapter that particles first begin to travel in suspension when the vertical component of turbulence (or, more precisely, the normal-to-the-bed component of the turbulence) becomes about equal to the settling velocity of the particles (Equation 10.3.2). As noted earlier, there is no natural way to characterize the magnitude of this fluctuating component of the vertical fluid velocity, because it fluctuates over a wide range of values; the rms value is usually used to characterize its magnitude for this purpose. Contrary to a view that has sometimes been expressed in the literature, suspension does not depend on asymmetry in the frequency distribution of the vertical fluctuating velocities: provided that at least some of the vertical fluctuations are greater than the settling velocities of the particles, some of the particles experience suspension, even if the frequency distribution of fluctuating velocities is asymmetrical, because the conditions would still be conducive to diffusion (see Chapter 1): random motions of the medium, in combination with an upward gradient in sediment concentration, from nonzero in the bed-load layer to some smaller value, perhaps even zero, at some greater height above the bed. Such an asymmetry in the frequency distribution of vertical velocities might, however, affect the details of the concentration distribution.
Before dealing with the more important but more complicated case of suspension in a turbulent shear flow, we will look at suspension by homogeneous and isotropic turbulence. The characteristics of the turbulence do not vary from place to place within a certain region of the fluid, and neither do they vary with direction at any point within that region. Rouse (1939), the first to study sediment suspension in this way, produced a close approximation to isotropic turbulence by vertically oscillating an array of square grids in a large-diameter vertical cylinder (“turbulence jar”).
The downward volume flux of particles by settling, from a region in the fluid having a concentration \(C\) of uniform-size particles, is \(-wC\). It is reasonable to assume that the upward vertical diffusion of particles follows a Fickian diffusion law, like many other diffusion processes (see Chapter 1), so that the upward volume flux of particles by diffusion is \(\varepsilon_{S} d C / d y\), where \(\varepsilon_{S}\) is a diffusion coefficient, which should be constant in a field of isotropic turbulence of any particular type and strength, and the positive \(y\) direction is upward. Equating the two fluxes gives an expression for the vertical distribution of the concentration of suspended particles:
\[w C+\varepsilon_{S} \frac{d C}{d y}=0 \label{10.8} \]
The resulting expression for suspended sediment concentration as a function of height y above the bed, developed below, is sometimes called the diffusional theory of suspended-sediment concentration. It also seems reasonable that the diffusion coefficient \(\varepsilon_{S}\) is proportional to, if not actually equal to, the corresponding coefficient for the diffusion of fluid momentum, i.e., the kinematic eddy viscosity, and therefore in a turbulence jar it should be proportional to the frequency of vertical oscillation of the grid. Rouse verified that this is the case, thus confirming the validity of the diffusion equation (see also experimental results reported by Antsyferov and Kos’yan, 1980).
In nature, homogeneous and isotropic turbulence is the exception; we have to deal with turbulence that typically varies in its characteristics with distance from the boundary, and at least to some extent with direction, mainly normal to the boundary at any point. In a turbulent shear flow, as for example, in a river, a tidal current, or a strong wind, where turbulence is not even approximately homogeneous and isotropic except perhaps at large distances from the bed, we should expect that the diffusion coefficient varies in the direction \(y\) normal to the bed, so we need an expression that tells us how it varies with \(y\) before we can make use of Equation \ref{10.8} to predict how the sediment concentration varies with \(y\).
To find such an expression we assume the sediment diffusion coefficient \(\varepsilon_{S}\) to be proportional to the eddy viscosity \(\varepsilon\), given by
\[\tau=\rho \varepsilon \frac{d u}{d y} \label{10.9} \]
Assuming that \(\varepsilon_{S}=\beta \varepsilon\), then
\[\tau=\frac{\varepsilon_{S} \rho}{\beta} \frac{d u}{d y} \label{10.10} \]
where \(\beta\) is a coefficient that is likely to be close to one. You already know that \(\tau\) varies linearly with \(y\) in uniform open channel flow,
\[\tau=\tau_{\text{o}}\left(1-\frac{y}{d}\right) \label{10.11} \]
(see Chapter 4), so
\(\varepsilon_{S}=\frac{\frac{\beta \tau_{\text{o}}}{\rho}\left(1-\frac{y}{d}\right)}{\frac{d u}{d y}}\)
\[=\frac{\beta u_{*}^{2}\left(1-\frac{y}{d}\right)}{\frac{d u}{d y}} \label{10.12} \]
Using the law of the wall in differential form (Chapter 4),
\[\frac{d u}{d y}=\frac{u_{*}}{\kappa y} \label{10.13} \]
we have
\[\varepsilon_{S}=\beta u_{*}\left(1-\frac{y}{d}\right) \kappa y \label{10.14} \]
Equation \ref{10.14} is the relationship between \(\varepsilon_{S}\) and \(y\) that we need in order to solve Equation \ref{10.10}. Combining Equations \ref{10.8} and \ref{10.14} gives
\[\frac{d C}{C}=\frac{-w d y}{\beta \kappa u_{*}\left(1-\frac{y}{d}\right) y} label{10.15} \]
which can be integrated to give the equation first derived by Rouse (1937):
\[\ln C=\frac{w}{\beta \kappa u_{*}} \int_{a}^{d} \frac{d y}{\left(1-\frac{y}{d}\right) y} label{10.16} \]
or
\[\frac{C}{C_{a}}=\left(\frac{d-y}{y} \frac{a}{d-a}\right)^{z} \label{10.17} \]
where
\[z=\frac{w}{\beta \kappa u_{*}} \label{10.18} \]
The exponent \(z\) is sometimes called the Rouse number.
You can see from Equations \ref{10.17} and \ref{10.18} that the larger the value of \(z\), the more rapidly the suspended-sediment concentration decreases with height above the reference level \(a\). Equation \ref{10.17}, graphed in Figure \(\PageIndex{1}\), gives the concentration of suspended sediment of a given settling velocity \(w\) at a height \(y\) above the bed relative to its concentration \(C_{a}\) at an arbitrarily chosen “reference level” \(y = a\) above the bed.
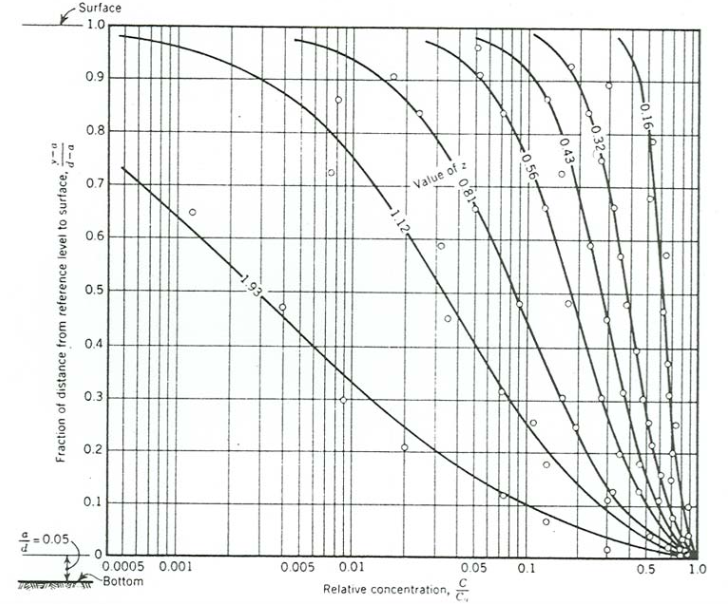
Ideally, the reference concentration \(C_{a}\) would be taken to be as close to the bed as possible but still far enough above the bed that a balance between downward settling and upward turbulent diffusion of suspended sediment is physically reasonable. The theory fails very close to the bed, because a balance between passive upward turbulent diffusion and downward settling is not applicable there: particle movements at and very near the bed are controlled by fluid lift and drag forces, and if concentrations are high these movements may be significantly affected by collisions or interactions between particles. The reference height a above the bed is most naturally just above the bed-load layer. This is consistent with the idea that the sediment concentration at the top of the bed-load layer acts as a lower boundary condition for the distribution of suspended sediment higher in the flow. This points up the problem of specifying the suspended-sediment concentration in absolute rather than relative terms: no successful theory has been developed yet for the bed-load concentration as a function of flow and sediment conditions. Because the structure of the flow and the dynamics of bed-load movement are so complex in the near-bed layer when the flow is strong enough to move sediment in suspension, no elegant way has been developed to put this appealing idea, that the bed load forms the lower boundary condition for the suspended load, into useful practice.
Experiments to test Equation \ref{10.19} were reported by Vanoni (1946). These experiments were mostly made at relatively high velocities over a planar bed (either a sand bed or the rigid floor of the flume) and at varying concentrations of sand. Vanoni found a general agreement between predicted and observed sediment concentrations (Figure \(\PageIndex{1}\)).
Because both \(\beta\) and \(\kappa\) are supposed to be constants, the main factor that determines the distribution of suspended sediment with height \(y\) above the bed should be the ratio of the settling velocity \(w\) to the shear velocity \(u_{*}\). It was suggested in an earlier section of this chapter that a critical ratio of about one determines whether any particles will go into suspension: since \(\beta \approx 1\) and \(\kappa \approx 0.4\), \(w/u_{*}\) less than one corresponds to \(z\) less than \(2.5\). We can see from Figure \(\PageIndex{1}\) that at values of \(z\) greater than \(2.5\) any sediment in suspension would be concentrated in a zone very close to the bed—and this tends to confirm the choice of \(w/u_{*}\) as a suitable criterion for suspension.
Two factors in open-channel flows have a direct effect on the ratio \(w/u_{*}\) and therefore on the vertical profile of suspended-sediment concentration: viscosity, and friction. First the viscosity: for a given particle size and shape, \(w\) is reduced by an increase in the viscosity sensed by the settling particles. That can be brought about in two ways: a reduction in the temperature of the fluid, which increases the viscosity of the fluid itself, or an increase in the wash-load concentration. In the latter case, the viscosity of the fluid remains the same but the effective viscosity of the deformable medium (the fluid charged with wash load) that is sensed by the particles of the suspended bed-material load, which are much larger than the particles of the wash load, is greater. Both of these effects act to reduce the ratio \(w/u_{*}\), and hence the Rouse number \(z\), and make sediment more uniformly distributed in the vertical (Equation \ref{10.19}). The fluid-viscosity effect diminishes with increasing settling-velocity Reynolds number, however, and becomes unimportant when the range of Reynolds numbers for which the drag coefficient is approximately constant is reached; see Chapter 2.
Now for the effect of friction: for a given mean flow velocity, an increase in the coefficient of bottom friction causes an increase in bottom shear stress, and therefore in shear velocity. To see why, go back to the definition of the friction factor \(f\) (Equation 4.7.7 in Chapter 4): \(\tau_{\text{o}} = (f/8)\rho U^{2}\), or \(U/u_{*} = (8/f)^{1/2}\). So an increase in the shear velocity also results in a more uniform vertical distribution of suspended sediment, by decreasing the ratio \(w/u_{*}\). In sand-bed rivers, changes in f are produced mainly by changes in the relative roughness, which depends mainly on the nature and size of the bed forms. Large bed forms, like dunes, produce large values of \(f\), and therefore cause suspended bed-material sediment to be distributed more uniformly in the vertical than if the bed were planar. In fact, it is been observed in flume studies that the vertically averaged suspended-sediment concentration actually decreases somewhat in the transition from a dune-covered sand bed to an upper-regime plane bed, with its accompanying decrease in flow resistance, as the flow velocity increases.
The theory of suspension by turbulent flows outlined above is based on the assumption that the flow is steady. This is be a reasonable approximation for most rivers, but tidal currents change quite rapidly in both depth and speed over the tidal cycle. It has been shown that in experimental turbulent shear flows, decelerating flows have larger turbulence intensities, and produce larger shear stresses on the bed, than steady flows. Decelerating flows therefore might be expected to be more erosive, and to have a higher capacity for suspended sediment, than steady or accelerating flows. Wimbush and Munk (1970), Gordon and Dohne (1973), Gordon (1975), Bohlen (1977), and McCave (1979) have reported measurements suggesting that turbulence intensities are higher than normal during deceleration of flows on both flood and ebb tides. Gordon (1975) and Bohlen (1977) have commented on the implications for transport of suspended sediment by tidal currents, but convincing direct evidence of the effect of deceleration on sediment transport by tidal currents is still lacking.
The diffusional theory of suspension presented above is based on the assumption that turbulence diffuses sediment according to a simple (“Fickian”) diffusion law. This assumption is in reasonably good accord with experiment, but it is not the only possible basis for a theory of sediment suspension. Alternative theories, based on different assumptions, are described by Nordin and McQuivey 1971), Drew (1975; see also Drew and Kogelman, 1975), Willis (1979), Herczynski and Pienkovska (1980), and McTigue (1981), among others.
Although the diffusional theory of sediment suspension has been described as “the brightest analytical achievement to date in the field of river hydraulics” (Hsu et al., 1980; see also Kennedy, 1984, p. 1257), in that it represents an elegant and rational theoretical approach, based on reasonably well understood physical effects, that does quite well in its predictions without relying upon any suspicious “fudge factors”, it is subject to a number of criticisms:
- The theory takes no account of the details of how the sediment particles are actually handled by the eddies in the turbulent flow field. There are two different aspects to this. One has to do with the interesting and counterintuitive effect of the tendency of eddies to trap sediment particles (Tooby et al. 1977; Nielsen, 1984), discussed briefly in Chapter 3. The other is that the theory assumes turbulence that is isotropic in its vertical motions, i.e., that the frequency distribution of the vertical velocity is symmetrical. There is good reason to believe, however, that close to the bed the vertical component is anisotropic (Leeder 1983a, 1983b): the less common upward motions are stronger than the more common downward motions in this region, as would be expected from the semicoherent burst–sweep structure of the near-bed turbulence (Chapter 4). As first proposed by Bagnold (1966), and further developed by Leeder (1983a, 1983b), the anisotropy in vertical turbulent velocities is what maintains sediment in suspension—with the implication that without this anisotropy the concentration of sediment in suspension would be much less. The flaw in this concept is that, to maintain balance of fluid masses passing upward and downward in the turbulence field, the downward-moving eddies must cover a greater area, in any plane through the flow that is parallel to the bottom boundary, than the upward-moving eddies, thus maintaining a balanced exchange of sediment even in the face of the vertical anisotropy of turbulence. Despite some assertions in the literature to the contrary, such anisotropy is only a minor distorting effect on the diffusional theory, and is not a necessary condition for the maintenance of bed-material sediment in suspension.
- Vanoni (1946, and many subsequent investigations reported and analyzed in Vanoni, 1975) found that in some experiments, particularly those in which there was a high concentration of coarse sediment close to the bed, the value of the supposedly universal von Kármán constant decreased from its accepted value of \(0.38\) to values as low as \(0.2\). He interpreted this as indicating that the presence of sand moving close to the boundary changed the structure of turbulence in the flow. The von Kármán constant \(\kappa\) plays a fundamental role in the diffusional theory of suspended sediment, by virtue of its effect on the gradient of time-average flow velocity in the law of the wall (Equation \ref{10.15}); if \(\kappa\) is itself affected nonnegligibly by the presence of suspended sediment, then it becomes part of the problem rather than an independent input to the problem, and the theory would become much more complicated.
- Besides the uncertainty about \(\kappa\), several authors have reported large deviations of \(\beta\) from the expected value close to unity. There are reasons to expect that solid particles are not diffused at the same rate as fluid momentum, and that the ratio of the two rates of diffusion is not a constant but varies with the properties of both the sediment and the fluid turbulence. At present there is no satisfactory way to predict the value of \(\beta\). Prediction presumably will become possible only when there is a better understanding of the mechanism of diffusion.
- In the usual theory the sediment diffusion coefficient is assumed to be proportional to the eddy viscosity and the distribution with depth to be given by Equation \ref{10.18}. This equation predicts that \(\varepsilon_{S}\) (and \(\varepsilon\)) drop slowly to zero as the free surface is approached. Because sediment cannot diffuse through the free surface, \(\varepsilon_{S}\) must be equal to zero there. Coleman (1970) has, however, calculatedεs directly from observed values of \(C\) and \(dC/dy\) using Equation \ref{10.8}. He found that there is a strong dependence on depth only near the bed; over most of the flow, and even quite close to the free surface, \(\varepsilon_{S}\) appears to be independent of depth.
For all of these reasons, the diffusional theory of sediment suspension, though it is a better theory than that available for most aspects of sediment transport, must still be regarded as somewhat less than completely satisfactory.
A Note on the Effect of Acceleration of Gravity on Sediment Movement
It is worthwhile to consider how sediment movement and bed configurations in water flows might differ where the acceleration of gravity is different. Back in Chapter 8, in the section on dimensionless variables), a set of dimensionless variables was developed in which the leading variables in a sediment-transport system,—variables with dimensions of length, like particle size, or variables with dimensions of velocity—can be organized in such a way that each of the leading variables in sequestered in its own dimensionless version. In each such variable, the acceleration of gravity enters as well. If gravity is different, any length or velocity variable in a dynamically similar system must then also be different. Southard and Boguchwal (1990) show that, in the case of Mars, for which the acceleration of gravity is only about \(0.4\) times that of Earth, a length variable on Mars would be about \(1.36\) times that on Earth, and a velocity variable on Mars would be about \(0.74\) times that on earth, for a dynamically similar system.
References Cited Chapter 10
Abbott, J.E., and Francis, J.R.D., 1977, Saltation and suspension trajectories of solid grains in a water stream: Royal Society [London], Philosophical Transactions, v, 284, p. 225-254.
Antonia, R.A., and Luxton, R.E., 1971, The response of a turbulent boundary layer to a step change in surface roughness, Part 1, smooth to rough: Journal of Fluid Mechanics, v. 48, p. 721-761.
Antsyferov, S.M., and Kos'yan, R.D., 1980, Sediments suspended in stream flow: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 106, p. 313-330.
Bagnold, R.A., 1954, Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear: Royal Society [London], Proceedings, v. A225, p. 49-63.
Bagnold, R.A., 1956, The flow of cohesionless grains in fluids: Royal Society [London], Philosophical Transactions, v. A249, p. 235-297.
Bagnold, R.A., 1966, An approach to the sediment transport problem from general physics: U.S. Geological Survey, Professional Paper 422-I, 37 p.
Bagnold, R.A., 1973, The nature of saltation and of “bed load” transport in water: Royal Society [London], Proceedings, v. A332, p. 473-504.
Blinco, P.H., and Partheniades. E., 1971, Turbulence characteristics in free surface flows over smooth and rough boundaries: Journal of Hydraulic Research v. 9, no. 8, p. 43-69.
Bohlen. W.F., 1977, Shear stress and sediment transport in unsteady turbulent flows: in Wiley, M., ed., Estuarine Processes. Vol. I. Uses, Stresses, and Adaptation to the Estuary, p. 109-123: New York, Academic Press, Vol. 2, 541 p
Bradley. W.C.. Fahnestock, R.K., and Rowekamp, E.T., 1972, Coarse sediment transport by flood flows, Knik River, Alaska: Geological Society of America, Bulletin, v. 83, p. 1261-1284.
Bridge, J.S., 1978, Origin of horizontal lamination under turbulent boundary layers: Sedimentary Geology, v. 20, p. 1-16.
Coleman, N.L., 1970, Flume studies of the sediment transfer coefficient: Water Resources Research, v. 6, p. 801-809.
Drake, T.G., Shreve, R.L., Dietrich, W.E., Whiting, P.J., and Leopold, L.J., 1988, Bedload transport of fine gravel observed by motion-picture photography: Journal of Fluid Mechanics, v. 192, p. 193-217.
Drew, D.A., 1975, Turbulent sediment transport over a flat bottom using momentum balance: Journal of Applied Mechanics, v. 42, p. 38-44.
Drew, D.A., and Kogelman, S., 1975, Turbulent sediment transport using momentum balance—the strong turbulence approximation: Applied Science Research, v. 30, p. 279-290.
Dzulynski, S., and Sanders, J.E., 1962, Current marks on firm mud bottoms: Connecticut Academy of Arts and Sciences, Transactions, v. 42, p. 57-96.
Einstein, H.A., 1950, The bed-loan function for sediment transportation in open channel flows: U.S. Department of Agriculture, Technical Bulletin 1026, 70 p. (reprinted as Appendix B in Shen, H.W., ed. 1972, Sedimentation, Fort Collins, Colorado).
Einstein, H.A., and Chien, N., 1955, Effects of heavy sediment concentration near the bed on velocity and sediment distribution: U.S. Army Corps of Engineers, Missouri River Division, M.R.D. Sediment Series no. 8, 76 p.
Fernandez Luque, R., 1974, Erosion and Transport of Bed-Load Sediment: Ph.D. Thesis, Technical Highschool, Delft, Holland, Krips. Repro. B.V., Meppel, 65 p. plus tables and figs.
Fernandez Luque, R., and Van Beek, R., 1976, Erosion and transport of bed-load sediment: Journal of Hydraulic Research, v. 14, p. 127-144.
Francis, J.R.D., 1973, Experiments on the motion of solitary grains along the bed of a water-stream: Royal Society [London], Proceedings, v. A332, p. 443-471.
Gordon, C.M., 1975, Sediment entrainment and suspension in a turbulent tidal flow: Marine Geology, v. 18, p. M57-M64.
Gordon, C.M., and Dohne, C.F., 1973, Some observations on turbulent flows in a tidal estuary: Journal of Geophysical Research, v. 78, p. 1971-1978.
Gordon, R., Carmichael, J.B., and Isackson, F.J., 1972, Saltation of plastic balls in a “one- dimensional” flume: Water Resources Research, v. 8, p. 444-459
Grass, A.J., 1971, Structural features of turbulent flow over smooth and rough boundaries: Journal of Fluid Mechanics, v. 4, p. 149-190.
Grass, A.J.. 1974, Transport of fine sand on a flat bed: turbulence and suspension mechanics: Technical University of Denmark, Proceedings Euromech 48, p. 33- 34.
Hamilton, W.S., and Courtney, G.L., 1977, Added mass of sphere starting upward near floor: American Society of Civil Engineers, Proceedings, Journal of the Engineering Mechanics Division, v. 103, p. 79-97.
Herczynski, R., and Pienkovska, I., 1980, Toward a statistical theory of suspension: Annual Review of Fluid Mechanics, v. 12, p. 237-269.
Hiscott, R.N., 1994, Traction-carpet stratification in turbidites—Fact or fiction?: Journal of Sedimentary Research, v. A64, p. 204-208.
Hiscott, R.N., 1995, Traction-carpet stratification in turbidites—Fact or fiction?—Reply: Journal of Sedimentary Research, v. A65, p. 704-705.
Hsu, S.T., van der Beken, A., Landweber, L., and Kennedy, J.F., 1980, Sediment suspension in turbulent pipe flow: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 106, p. 1783-1793.
Ippen, A.T., 1971, A new look at sedimentation in turbulent streams: Boston Society of Civil Engineers, Proceedings, v. 58, p. 131-161.
Jackson, R.G., 1976, Sedimentological and fluid dynamic implications of the turbulent bursting phenomenon in geophysical flows: Journal of Fluid Mechanics, v. 77, p. 531-560.
Kalinske, A.A., 1943, Turbulence and the transport of sand and silt by wind: New York Academy of Science, Annals, v. 44, p. 41-54.
Karcz, I., 1973, Reflections on the origin of some small-scale longitudinal streambed scours in Morisawa, M., ed., Fluvial Geomorphology: 4th Annual Geomorphology Symposium, Proceedings, State University of New York at Binghamton, Publications in Geomorphology, p. 149-173.
Kennedy, J.F., 1984, Reflections on rivers, research and Rouse: Journal of Hydraulic Engineering, v. 109, p. 1254-1271.
Krumbein, W.C., 1942, Settling velocity and flume-behavior of non-spherical particles: American Geophysical Union, Transactions v. 23, p. 621-632.
Lane, E.W., and Carlson, E.J., 1954, Some observations on the effect of particle shape on the movement of coarse sediments: American Geophysical Union, Transactions, v. 35, p. 453-462.
Leeder, M.R., 1983a, On the interactions between turbulent flow, sediment transport and bedform mechanics in channelized flow: International Association of Sedimentologists, Special Publication 6, p. 5-18.
Leeder, M.R., 1983b, On the dynamics of sediment suspension by residual Reynolds stresses—confirmation of Bagnold’s theory: Sedimentology, v. 30, p. 485-491.
Mantz, P.A., 1977, Incipient transport of fine grains and flakes by fluids—extended shields diagram: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 103, p. 601-615.
McCave, I.N., 1979, Tidal currents at the North Hines Lightship, southern North Sea: Flow directions and turbulence in relation to maintenance of sand bars: Marine Geology, v. 31, p. 101-113.
McQuivey, R.S., and Richardson, E.V., 1969, Some turbulence measurements in open- channel flows: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 95, p. 209-223.
McTigue, D.F., 1981, Mixture theory for suspended sediment transport: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 107, p. 659- 673.
Meland, N., and Norrman, J.O., 1966, Transport velocities of single particles in bed-load motion: Geografiska Annaler, v. A48, p. 165-182.
Middleton, G.V., 1976, Hydraulic interpretation of sand size distributions: Journal of Geology, v. 84, p. 405-426.
Moss, A.J., 1972, Bed-load sediments: Sedimentology, 18, p. 159-219.
Murphy, P.J., and Hooshiari, H., 1982, Saltation in water dynamics: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 108, p. 1251- 1267.
Nakagawa, H., and Tsujimoto, T., 1980, Statistical analysis of sediment motions on dunes—discussion: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 106, p. 221-226.
Nielsen, P., 1984, On the motion of suspended sand particles: Journal of Geophysical Research, v. 89, p. 616-626.
Nordin, C.F., and McQuivey, R.S., 1971, Suspended load, in Shen, H.W., ed., River Mechanics, Vol 1, p. 12-1–12-30.
Rouse, H., 1937, Modern conceptions of the mechanics of turbulence: American Society of Civil Engineers, Transactions, v. 102, p. 436-505.
Rouse, H., 1939, Experiments on the mechanics of sediment suspension: 5th International Congress on Applied Mechanics, Cambridge, Mass., p. 550-554.
Sohn, Y.K., 1995, Traction-carpet stratification in turbidites—fact or fiction?— Discussion: Journal of Sedimentary Research, v. A65, p. 703-705.
Southard, J.B., and Boguchwal, L.A., 1990, Bed configurations in steady unidirectional water flows. Part 3. Effects of temperature and gravity: Journal of Sedimentary Petrology, v. 60, p. 680-686.
Sumer, B.M., and Deigaard, R., 1981, Particle motions near the bottom in turbulent flow in an open channel, Part 2: Journal of Fluid Mechanics, v. 109, p. 311-337.
Sumer, B.M., and Oguz, B., 1978, Particle motions near the bottom in turbulent flow in an open channel: Journal of Fluid Mechanics, v. 86, p. 109-128.
Tooby, P.F., Wick, G.L., and Isaacs, J.D., 1977, The motion of a small sphere in a rotating velocity field: a possible mechanism for suspending particles in turbulence: Journal of Geophysical Research, v. 82, p. 2096-2100.
Vanoni, V.A., 1946, Transportation of sediment in suspension: American Society of Civil Engineers, Transactions, v. 111, p. 67-133,
Vanoni, V.A., 1964, Measurements of critical shear stress for entraining fine sediments in a boundary layer: California Institute of Technology, W. M. Keck Laboratory of Hydraulics and Water Resources, Report KH-R-7, 47 p.
Vanoni, V.A., ed., 1975, Sedimentation Engineering: American Society of Civil Engineers, Manuals and Reports on Engineering Practice, No. 54, 745 p.
Willetts, B., 1998, Aeolian and fluvial grain transport: Royal Society (London), Philosophical Transactions, v. A356, p. 2497-2513.
Williams, G., 1964, Some aspects of the eolian saltation load: Sedimentology, v. 3, p. 257-287.
Willis, J.C., 1979, Suspended load from error-function models: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 105, p. 801-816.
Wimbush, M., and Munk, W., 1970, The benthic boundary layer, in Maxwell, A. E., ed., The Sea, Vol. 4, Part 1, Ch. 19, p. 31-758: New York, Wiley-Interscience, 791 p.


