4.2: Laminar Flow Down an Inclined Plane
- Page ID
- 4170
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we apply Newton’s second law to steady and uniform flow down an inclined plane. The strategy is to look at a block of the flow, bounded by imaginary planes normal to the bottom, with unit cross-stream width and unit streamwise distance (Figure \(\PageIndex{1}\)). In fluid dynamics, such a block of fluid is said to be a “free body”. Because the flow is assumed to be steady and uniform, all of the forces in the streamwise direction that are exerted upon the fluid within the free body at any given time must add up to be to zero.
I should mention at the outset that for now I will not address how the flow is arranged so that the flow is uniform. If you just pour a sheet of water onto the plane along some particular horizontal line on the plane, you should not expect that uniform flow will automatically be established downslope of that line in the sense that the flow depth is the same at all normal-to-flow sections farther down the plane, and in general it is not: you would need to adjust the slope of the plane to attain a state of uniformity. This is not a trivial problem, and it should await some more detailed material, later in this chapter, on flow resistance. On the other hand, it should make intuitive sense to you that if the plane is very long the degree of nonuniformity would be very small whatever the slope: just imagine pouring water from a row of little faucets onto a plane a mile long and sloping a few degrees.
Obviously only liquids, not gases, can flow as open-channel flows. The freely deformable upper surface of the liquid, called the free surface, is open to the air. We will neglect the minor forces exerted by the overlying air on the moving liquid. Our idealized channel flow is of infinite width, with no side boundaries, and it is therefore just a convenient abstraction. But a flow in a channel of rectangular cross section with the width of flow much greater than the depth of flow is a good approximation to a flow with infinite width.
Take the \(x\) direction to be downstream and the y direction to be normal to the boundary, with \(y = 0\) at the bottom of the flow (Figure 4-1). By the no-slip condition, the velocity is zero at \(y = 0\), so the velocity must increase upward in the flow. It is also clear that the flow is everywhere directed straight down the plane. Think about the forces acting on the fluid contained at a given instant in the free body within the rectangular volume formed by the free surface, the bottom boundary, and two pairs of imaginary planes normal to the bottom and with unit spacing, one pair parallel to the flow and spaced a distance \(B\) apart, and the other normal to the flow and spaced a distance \(L\) apart (Figure \(\PageIndex{1}\)).
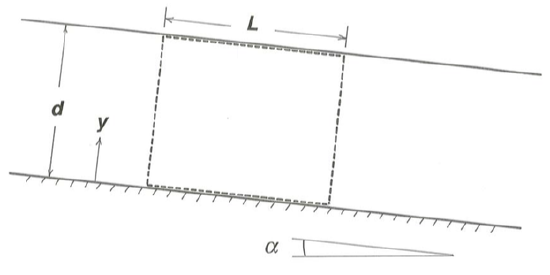
Writing Newton’s second law for the balance of forces on this free body means equating the downslope driving force, caused by the downslope component of the weight of the fluid in the free body, with the resistance force exerted by the planar boundary on the lower surface of the free body. The weight of the fluid in the free body is \(\gamma B L d\), where \(d\) is the depth of flow. The downslope component of this weight is \(\gamma \sin \alpha B L d\), where \(\alpha\) is the slope angle of the plane (Figure \(\PageIndex{2}\)).
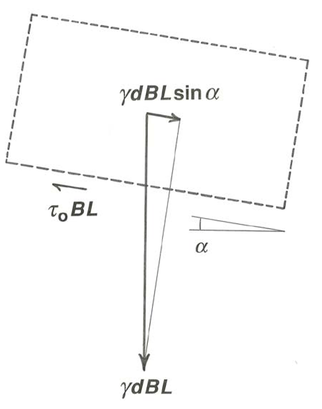
This is balanced by the frictional force \(\tau_{\text{o}} B L\) exerted by the bottom boundary. There are also pressure forces acting parallel to the flow direction on the upstream and downstream faces of the free body, but because by our assumption of uniformity the vertical distribution of these pressure forces is the same at every cross section, they balance each other out and cause no net force on the free body. Setting \(\gamma \sin \alpha B L d\) equal to \(\tau_{\text{o}} B L\) and solving for \(\tau_{\text{o}}\),
\[\tau_{\text{o}}=\gamma d \sin \alpha \label{4.1} \]
so the boundary shear stress is directly proportional to the product of the flow depth, the specific weight of the liquid, and the sine of the slope angle.
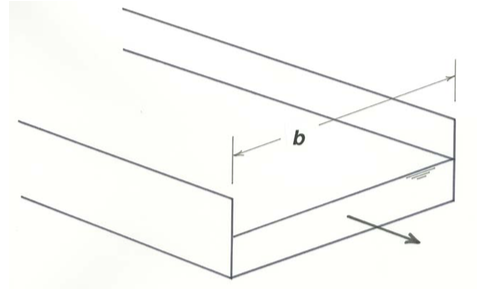
Before we continue with the development, we will make the resistance equation more relevant to the real world by writing a similar equation for a channel with rectangular cross section and then for a channel with arbitrary (but unvarying) cross section. To generalize Equation \ref{4.1} to a rectangular channel, take the flow width to be \(b\) (Figure \(\PageIndex{3}\)) and write the force balance for a free body that fills the channel, from wall to wall, in a segment of length \(L\) along the flow. Doing the same mathematics as above gives the result
\[\tau_{o}=\gamma \sin \alpha \frac{b d}{2 d+b} \label{4.2} \]
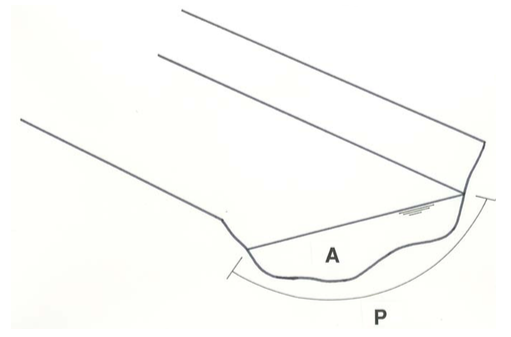
To generalize Equation \ref{4.1} to a channel of arbitrary cross-section shape, assume that the area of the cross section is \(A\) and the wetted perimeter (the distance along the submerged part of the boundary from waterline to waterline) is \(P\) (Figure \(\PageIndex{4}\)). The same balance of forces gives
\[\tau_{\text{o}}=\gamma \sin \alpha \frac{A}{P} \label{4.3} \]
Equations \ref{4.1}, \ref{4.2}, and \ref{4.3} look rather different, but they can easily be unified by defining a quantity called the hydraulic radius \(R_{H}\) formed by dividing the cross-sectional area of the flow by the wetted perimeter. You can verify for yourself that the hydraulic radius of flow in a rectangular channel is \(b d /(2 d+b)\). It is a little more difficult to see that the hydraulic radius of an infinitely wide channel flow is just the flow depth \(d\). You can reason that as the width \(b\) increases relative to the depth \(d\), the term \(2d\) in the denominator \(2d+b\) becomes a smaller and smaller part of the denominator, so the hydraulic radius \(bd/(2d+b)\) tends toward \(bd/b\), or just \(d\), as the width increases relative to the depth. The right-hand sides of all three equations, \ref{4.1}, \ref{4.2}, and \ref{4.3}, become \(\gamma \sin \alpha R_{H}\).
Equation \ref{4.3}, or its special cases Equation \ref{4.1} or Equation \ref{4.2}, is the basic resistance equation for steady uniform flow in an open channel. Not many useful results in fluid mechanics are so easily derived! It is the principal way that the boundary shear stress is found in rivers (although to use it that way you need to do some surveying to establish the elevation of the water surface at two points along the channel, at least hundreds if not thousands of meters apart). Sometimes the three equations are written in terms of the slope, \(\tan \alpha\), rather than the sine of the slope angle, \(\sin \alpha\), because for very small \(\alpha\) (the usual case), the approximation \(\sin \alpha \approx \tan \alpha\) is a good one.
Now back to the infinitely wide flow down a plane: now that you know how to find the boundary shear stress, what can be said about how the shear stress and flow velocity within the flow vary with height above the bottom? One thing you already know for sure: by the no-slip condition, the velocity at the very bottom must be zero. Another thing you can say without further derivation is that the velocity must be at its maximum at the free surface. Why? Because the downslope driving force of gravity is a “body force” that acts throughout the flow, whereas resisting friction force acts only at the bottom. The flow velocity must therefore increase monotonically upward in the flow.
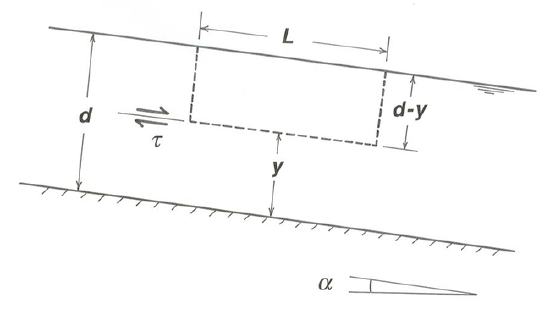
We can find the shear stress and velocity at all points up in the flow by applying the same force-balancing procedure to a free body of fluid similar to that used above but with its lower face formed by an imaginary plane a variable distance \(y\) above the bottom and parallel to it (Figure \(\PageIndex{5}\)). The shear stress \(\tau\) across the plane is given directly by the force balance:
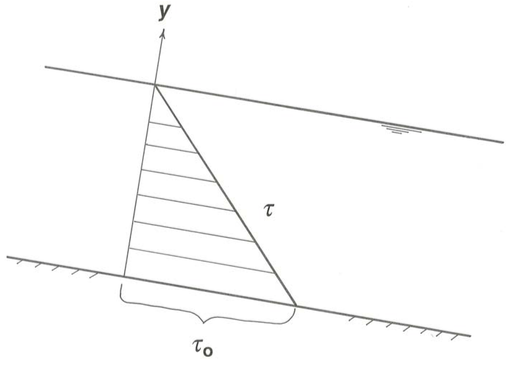
\[\tau=\gamma \sin \alpha(d-y) \label{4.4} \]
Using Equation \ref{4.1} to eliminate \(\gamma \sin \alpha\) from Equation \ref{4.4}, we can write \(\tau\) in terms of the boundary shear stress \(\tau_{\text{o}}\):
\[\tau=\tau_{\text{o}}\left(1-\frac{y}{d}\right) \label{4.5} \]
Equation \ref{4.5} shows that \(\tau\) varies linearly from a maximum of \(\gamma \sin \alpha\) at the bottom to zero at the surface (Figure 4-6).
Eliminating \(\tau\) from Equation \ref{4.4} by use of Equation 1.3.6 gives an expression for the velocity gradient \(du/dy\):
\(\mu \frac{d u}{d y}=\gamma \sin \alpha(d-y)\)
\[\frac{d u}{d y}=\frac{\gamma \sin \alpha}{\mu}(d-y) \label{4.6} \]
Equation \ref{4.6} can be integrated to give the velocity distribution from the bottom boundary to the free surface:
\(\begin{aligned} u &=\int \frac{d u}{d y} d y \\ &=\int \frac{\gamma \sin \alpha}{\mu}(d-y) d y \\ &=\frac{\gamma \sin \alpha}{\mu}\left(d \int d y+\int y d y\right) \\ &=\frac{\gamma \sin \alpha}{\mu}\left(y d+\frac{1}{2} y^{2}\right)+c \end{aligned}\)
We can evaluate the constant of integration \(c\) by use of the boundary condition that \(u = 0\) at \(y = 0\); we find that \(c = 0\), so
\[u=\frac{\gamma \sin \alpha}{\mu}\left(y d+\frac{1}{2} y^{2}\right) \label{4.7} \]
For given values of \(\gamma\), \(\alpha\), \(\mu\), and \(d\), the velocity \(u\) thus varies parabolically from zero at the bottom boundary to a maximum at the surface (Figure \(\PageIndex{7}\)). On the other hand, from Equation \ref{4.7} the velocity gradient \(du/dy\) varies linearly from a maximum at the bottom to zero at the free surface, because it is directly proportional to the shear stress (Figure \(\PageIndex{7}\)).
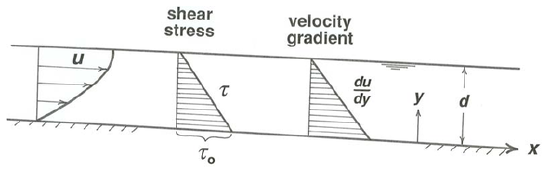
Here is a reminder about shearing within a flowing fluid, which you first encountered back in Chapter 1. You can think, loosely, in terms of layers of the fluid sliding past one another. A good way of making that concrete is to obtain a very thick telephone book and “rack” its pages by putting you hands firmly on the front and back covers and sliding them parallel to one another in the direction perpendicular to the spine of book. In fluids, of course, the shearing is continuous rather than in the form of discrete layers.


