1.4: Diffusion
- Page ID
- 4151
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Diffusion is the process by which matter, or properties carried by matter, like momentum, heat, solute, or suspended sediment, is transported from one part of a medium to another by random motions, molecular or macroscopic, in the presence of a spatial variation, or gradient, in average concentration of matter or the property. The essential factors in diffusion are thus the presence of random movements within the medium and a spatial gradient of some quantity or property. There cannot be diffusive transport without the concurrent existence of both conditions.
A good way to understand the nature of diffusion is to think about a simple hypothetical example. Suppose that you erect a vertical wall or barrier across the middle of a large room and manage somehow to fill one side of the room with white air molecules and the other side of the room with black air molecules (Figure \(\PageIndex{1}\)). At some particular time you instantaneously remove the barrier. Watch the exchange of speeding molecules across the plane once occupied by the barrier. In any small time interval the numbers of molecules passing in one direction across that plane is almost exactly equal to the numbers of molecules passing in the other direction, because the concentration of molecules stays the same everywhere, on the average, or else pressure differences from place to place would cause a net movement of air from higher pressure to lower pressure.
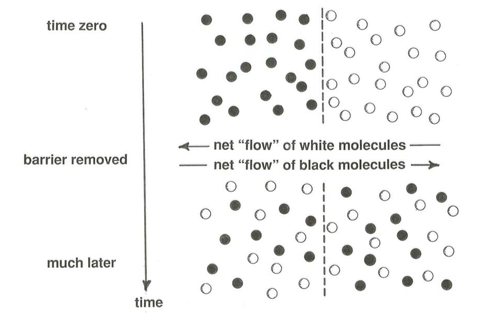
Immediately after the barrier is removed, all of the molecules moving from the “white” side to the “black” side are white and all of the molecules moving from the “black” side to the “white” side are black. At later times, after some of the white molecules have made their way over to the originally black side and some of the black molecules have made their way over to the white side, both white and black molecules move across the plane in each direction, but for a long time more white molecules than black move from the originally white side to the originally black side, and likewise more black molecules than white move from the originally black side to the originally white side.
This reveals the essence of diffusive transport: as the gradient of concentration of black and white molecules normal to the plane is made smaller by the diffusive transport, the rate of diffusive transport itself decreases; gradually the concentration gradients are evened out. Eventually, equal numbers of blacks and whites pass across the plane in either direction, and there is no more diffusive transport.
In simple diffusion of the kind exemplified above, the rate of diffusive transport, expressed as mass per unit time per unit area normal to the direction of diffusion (called the diffusive flux) is directly proportional to the concentration gradient in the direction of the diffusive flux. In the example above, you could convince yourself of this with just a little thought. This is expressed by the equation
\[F=-D \frac{\partial c}{\partial x} \label{flux} \]
where \(F\) is the rate of transport of mass per unit area, \(c\) is the mass concentration of the diffusing substance, and \(D\) is a proportionality coefficient called the diffusion coefficient. The minus sign is there because the diffusive transport is in the direction of decrease in \(c\) (“down the gradient”, in the parlance of physics). Diffusion can be more complicated than this: the diffusion coefficient might be a function of the concentration, and it might vary with direction at a point. We will not need to deal with such complications in these notes.
Viscosity as a Diffusion Coefficient
Viscosity can be interpreted as a diffusion coefficient for molecular momentum. Look at a small region of sheared fluid, and focus in on the collection of molecules in the vicinity of one of the shear planes (Figure \(\PageIndex{2}\)). Molecules are continually passing back and forth across the plane. The total mass of molecules passing in one direction is the same as the total mass passing in the other direction, but (and this is the essential point) the same kind of statement isnot true for transport, in the direction normal to the shear plane, of the component of molecule momentum taken normal to the shear plane and in the direction of average movement—just because, by the nature of shearing, the average velocity is greater on one side of the plane than the other. So random movements of molecules across the shear plane cause a normal-to-the-shear-plane transport of downflow component of momentum in the direction from higher flow speed to lower flow speed.
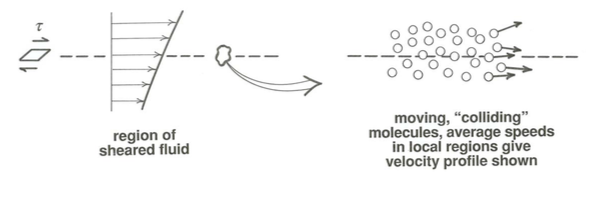
Applying the diffusion equation (Equation \ref{flux}) here, momentum transport rate \(=D \frac{d(\rho u)}{d y}\)
\[=\rho D \frac{d u}{d y} \label{11} \]
By Newton’s second law this spatial rate of change of momentum is equivalent to a force per unit area \(\tau\) on the shear planes:
\[\tau=\rho D \frac{d u}{d y} \label{12} \]
By comparing Equation \ref{11} with Equation \ref{12} you see that the viscosity \(\mu\) can be viewed as the diffusion coefficient for downflow momentum, multiplied by the fluid density \(\rho\). The physical interpretation here is that the on-the-average faster molecules that pass across the shear plane from the higher-velocity side to the lower-velocity side tend to speed up the molecules on the lower-velocity side, by eventually colliding with them and exerting actual forces on them, and conversely the on-the-average slower molecules that pass across the shear plane from the lower-velocity side to the higher-velocity side tend to slow down the molecules on the higher-velocity side. This mutual speeding-up and slowing-down has the effect of an actual surface contact force across the plane, of the sort you would associate with, say, the sliding of a brick on a tabletop—but remember that there is no slip along the shear planes in the fluid.


