10.4: Bed Load
- Page ID
- 4214
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Styles of Bed-Load Movement at Low Flow Intensities
Transport of the surficial particles on a locally planar bed produces a distinctive microtopography, consisting of small-scale irregular and discontinuous ridges and depressions oriented approximately parallel to the flow. The spacing of these features on a sand bed is of the order of several millimeters, and the relief is very small, generally only a few particle diameters. This lineated relief is a characteristic feature of transport, for particles ranging from silt sizes (Mantz, 1977) up to at least very coarse sand, and for hydraulic conditions ranging from just above the threshold of particle movement to high flow intensities that produce upper-regime, plane-bed conditions. It is the manifestation of the low-speeds streaks associated with the burst–sweep cycle, described in Chapter 4.
It does not take special experimental conditions to see manifestations of this lineated microtopography. Here are two everyday (well, almost) examples. It is a cold, gray day, and the snow has just begun to fall. Before the paved surface of the road is completely whitened, you see distinctive, shifting white streaks of snow aligned with the wind blowing across the road. Or you are standing at the kitchen sink, washing root vegetables fresh from the garden. The fine fraction of the loosened sediment is carried in suspension down the drain, never to be seen again, but the coarser fraction is immediately formed into small- scale streaks on the surface of the sink, beneath the fast-flowing water headed for the drain. Go back to the final section in Chapter 4, on coherent structures in turbulent flow, for the dynamics behind these bed-load streaks.
The ridges and depressions are produced by the action of small but strong turbulent eddies on the bed. Exactly how this takes place is becoming clearer as the structure of turbulence close to the bed becomes better understood as a result of numerous laboratory studies. The relevance of these observations to sediment movement has been discussed more thoroughly by Grass (1971, 1974), Karcz (1973), Jackson (1976), Sumer and Oguz (1978), Bridge (1978), Sumer and Deigaard (1981), and Leeder (1983a).
Most experimental observations have been made on boundaries that are dynamically smooth or transitionally rough, i.e., on boundaries characterized by a viscous sublayer that is at least poorly developed. But observations of dynamically rough boundaries (e.g., by Grass, 1971) show that even for flows without a viscous sublayer there exists a region close to the boundary, which Grass called the “inner zone”, for \(y^{+} < 40\), characterized by distinctive low-speed longitudinal streaks and a quasi-cyclic alternation of events that has come to be known as the burst–sweep cycle (see Chapter 4). As strong vortices with axes transverse to the flow approach the boundary, they produce pressure gradients that tend to lift up the streaks and eject them into the turbulent boundary layer. This “burst” of slow-moving fluid is capable of carrying small particles away from the bed to distances a few centimeters above the bed. Sumer and Oguz (1978) found that particles whose settling velocity was of the order of \(0.5 u_{*}\) were carried “in a single continuous motion” up to dimensionless elevations \(y^{+}\) of \(100–200\). The slow-moving fluid in the burst then mixes with, and is accelerated by, the fluid in the outer zone, and some returns to the bed as a fast-moving vortex or “sweep”, which in turn creates a new burst, and so on. The process is not strictly periodic, although on the average it displays a period and scale controlled mainly by the velocity and thickness of the turbulent boundary layer. If the period of bursts is \(T\) and the velocity far from the bed is \(U\), then \(U T / \delta=5\), where \(\delta\) is the thickness of the boundary layer (in an open-channel flow, the depth of the flow).
The existence of the burst–sweep cycle suggests an explanation of the phenomena of particle movement described above. The gusts of movement of particles along the bed described by many workers since Vanoni (1964) probably correspond to fluid sweeps in the burst-sweep cycle, when velocity gradients close to the bed, and therefore shear stresses, are locally high. Particles tend to be swept to one side or the other of fast-moving fluid streaks to gather under slow- moving streaks and produce the characteristic current lineation observed on plane beds.
For sand finer than about \(0.6\) \(\mathrm{mm}\), movement of particles over a plane bed eventually results in minor accumulations of particles that grow to form ripples (Chapter 11). The ripples then change the pattern of flow at the bed, and therefore also the interaction of the flow and the moving sediment particles. Separation of flow takes place at the ripple crest, and the boundary layer is reestablished downstream of where the flow reattaches to the bed, on the stoss side of the next ripple downstream. Although the bed surface is now much more irregular, the same lineated surface seen on a plane bed can generally be observed on the upper stoss sides of ripples or larger bed forms, if the water is clear and there is good low-angle lighting.
Perhaps the least difficult way of observing how bed-load particles move as the flow intensity increases beyond the threshold of movement is to study the movement of a single particle over a bed composed of similar particles that are held in place by an adhesive. The only problem with such experiments, although not a serious one, that is that there is no exchange between moving particles and the sediment bed: while not in motion, the test particle always rest high, in a very exposed position, and can never move into a low position (often called a pocket) recently vacated by another entrained particle. Such experiments have been reported by Meland and Norrman (1966), Francis (1973), Abbott and Francis (1977), and Nakagawa et al. (1980). Valuable as these single-particle studies are, however, there is no substitute for watching the motion of bed-load particles on real sediment beds. The observational difficulties are formidable: one needs clear water (no suspended load to obscure the view), a magnified close- up view, and, ideally, high-speed filming or video recording, because the rapidity with which the state of particle motion changes makes it not very productive to watch particle motions in real time.
Meland and Norrman (1966) distinguished three stages of particle motion:
- In the stage of “stop-and-go” movement, the particle is for a part of the time trapped between other particles on the bed. This stage follows initiation of motion and is especially typical of particles smaller than the average bed material. At this stage a very small increase in \(u_{*}\) above the critical value produces a marked increase in the average rate of particle movement, which however is controlled mainly by the bed and particle size.
- In the stage of continuous movement in contact with the bed, the particle rolls or skims over the surface of the bed.
- In the highest stage, particles begin to be lifted up above the bed level or to make long jumps. Increases in particle velocity are roughly proportional to increases in shear velocity.
Francis (1973) also distinguished three modes of movement, although they do not correspond exactly with the stages described by Meland and Norrman:
- rolling of particles in contact with the bed (roughly equivalent to stages 1 and 2 of Meland and Norrman);
- saltation, with particles rising up to heights of about two to four particle diameters above the bed and then falling back along “ballistic” paths, as illustrated in Figure \(\PageIndex{1}\); and
- suspension, in which at first particles move in “leaps” that are distinguished from saltation by their length and sinuous trajectories (Figure \(\PageIndex{1}\)), but as suspension becomes better developed the particles rise farther above the bed and return to it less often.
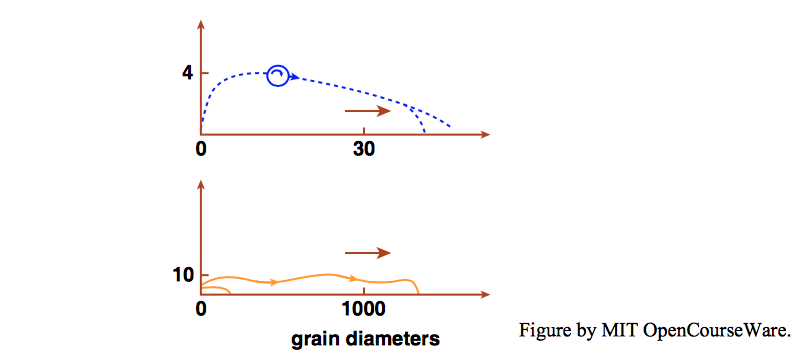
Francis (1973) distinguished saltation from suspension on the basis of a qualitative assessment of the particle trajectory. Abbott and Francis (1977, p. 229) suggested a more rigorous definition: a particle is in saltation when it “jumps away from the bed and follows such a trajectory that its vertical acceleration is always directed downwards between the upward impulses sustained while in contact with the bed.” If at any time the vertical acceleration is directed upwards, then the particle is regarded as being in suspension. According to this definition, whether or not a particle is in suspension cannot be determined simply from qualitative observation: a detailed analysis of the vertical component of its acceleration, based on high-speed photography of its trajectory, is needed. Further discussion of the nature of saltation (which is better developed in air than in water) will be deferred until we have examined some of the experimental results on the relation between flow intensity and rate of sediment movement. The mode of movement at shear velocities just above the threshold value \(u_{*c}\) predicted by the Shields diagram was investigated by Abbott and Francis (1977), with the results shown in Figure \(\PageIndex{2}\).
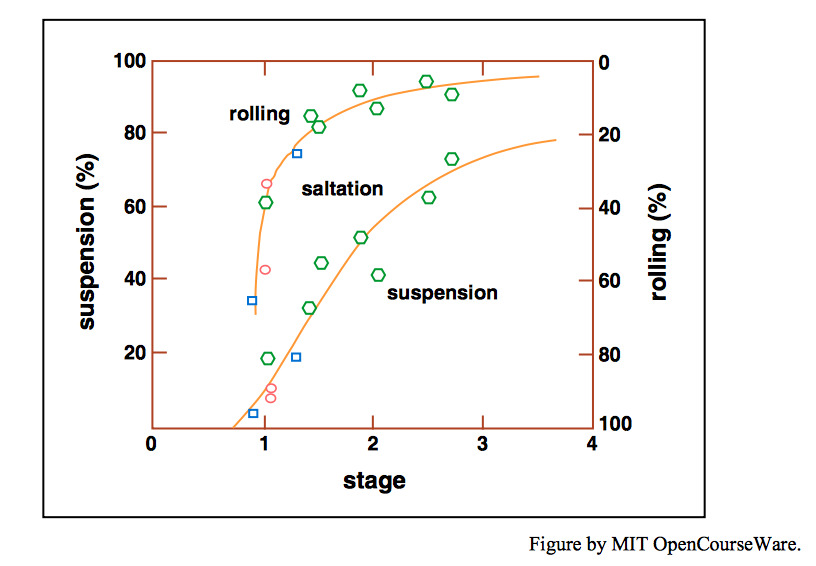
The earliest particle movements, at \(u_{*}/u_{*c}\) of about \(1\) (corresponding to \(u_{*}/w\) about \(0.15\)), are by rolling, but as the flow intensity increases, saltation rapidly becomes the dominant mode of particle movement. By the time \(u_{*}/w\) has reached values of only about \(0.3\), about \(50\%\) of the particle trajectories are classified as being in the suspension mode, using the strict definition of Abbott and Francis (1977), but the particles follow paths that are still very close to the bed, and the average speed of the particles, \(U_{G}\), is roughly proportional to the shear velocity. (\(U_{G}/u_{*}\) is about \(6\) to \(8\), indicating that the speed of the particle is almost equal to that of the flow close to the bed) At \(u_{*}/w = 0.5\) most trajectories would be classified by Abbott and Francis (1977) as in the suspension mode, but the particles are still moving mainly close to the bed in a mode that might be subjectively described by most observers as being more like saltation than true suspension.
As flow intensities are increased further, particle trajectories become longer and more irregular and the particles are carried higher into the flow. At these higher intensities it seems more reasonable to normalize the average speed of particle movement by dividing by mean flow velocity \(U\) (a property of the main flow) than by dividing by shear velocity \(u_{*}\) (a property of the flow just above the bed). Abbott and Francis (1977, and see Francis, 1973) found that for particles of equal density \(U_{G}/U\) was directly related to \(w/u_{*}\), the reciprocal of \(u_{*}/w\) (Figure \(\PageIndex{3}\)). At \(u_{*}/w\) greater than \(0.5\) the average particle speed was actually higher than the mean flow velocity, because most trajectories carried the particles up into the higher and therefore more rapidly moving parts of the flow. (Earlier experiments reported by Francis, 1973, suggest that in most cases \(U_{G}/U\) does not approach \(1\) until \(u_{*}/w\) approaches \(1\).) This is consistent with the suspension criterion, \(u_{*} > w\), introduced in an earlier section.
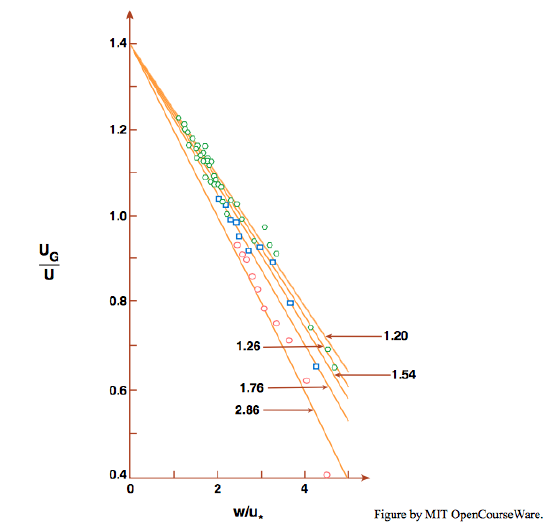
In his pioneer stochastic model for particle movement, Einstein (1950) postulated that the average distance traveled by a particle moving as bed load does not depend upon the flow intensity. Fernandez Luque (1974; see also Fernandez Luque and van Beek, 1976), in observations of particles moving over a loose planar bed at shear stresses only slightly larger than critical, found from direct observation that the average length of individual particle “steps” (or saltation jumps) was a constant equal to \(16\) times the particle diameter. Particles accelerated slightly at the beginning of each jump and decelerated upon returning to the bed but generally did not come to rest. On the average a particle jumped about \(18\) times, for a total step length of \(288\) particle diameters, before coming to rest. The average velocity while moving was reduced by collisions with the bed surface to about \(85\%\) of the maximum velocity achieved in each jump.
There have been few observational studies of the motions of bed-load particles in flows over loose rather than immobilized, sediment beds. Drake et al. (1988), in a study that shows how much information about particle motions can be obtained by carefully arranged observation, recorded the movements of bed-load particles on the bed of a clear-water stream by means of high-speed cinematography. The stream was \(6.45\) \(\mathrm{m}\) wide and \(0.35\) \(\mathrm{m}\) deep, and the bed consisted of moderately sorted sand and gravel with a median size of \(4\) \(\mathrm{mm}\). During filming, the bed shear stress was about \(6\) \(\mathrm{Pa}\), which was about twice the threshold for movement. There was active bed-load movement, but the concentration of bed load was not so great as to obscure the motions of the particles. The particles moved mainly by rolling, although the finest moved by saltation, and large, angular particles moved by brief sliding, pushing smaller particles out of the way. Displacement times for individual particles, which lasted for a few tenths of a second, were much shorter than repose times. Figure \(\PageIndex{4}\) shows representative trajectories of four particles, of various sizes, as seen in side view, taken from the motion-picture frames.

Effect of Shape
The movement of particles on the bed is strongly affected by their shape. Particles tend to become oriented on the bed by pivoting around other particles or resting against them, and they do not necessarily orient themselves with their maximum projection area normal to the flow, as they generally do during settling. Certain shapes—notably prolate forms (rollers) but also disks— roll more easily than others.
An early experimental study of the effect of shape was made by Krumbein (1942) using artificial ellipsoidal particles, all with the same nominal diameter, in a flume with a smooth bed. Depth was held constant at 0.3 m and velocity was varied by changing the slope. Krumbein found that, for a given fluid velocity, spheres and rollers moved fastest. Within any one shape class (e.g., rollers), particles velocity increased with increasing sphericity; the shape effect was greatest at low fluid velocities and particle velocities, and was less important as particles tended to be taken into suspension.
Lane and Carlson (1954) found that pebbles lining the beds of Colorado drainage canals were sorted by both size and shape. In a given sample of bed pebbles the disk-shaped pebbles had substantially smaller volumes than the more spherical pebbles—the opposite of what would be the case if the pebbles had the same settling velocity—indicating that spherical pebbles rolled more easily and were more easily set in motion than disk-shaped pebbles, which tended to assume more stable, imbricated orientations on the bed.
Bradley et al. (1972) studied the effect of shape both in the field (Knik River, Alaska) and in the laboratory. They detected downstream sorting of shapes, with platy pebbles being the most easily transported, then elongate pebbles (rollers), and more equant pebbles being the least easily transported. They recognized that the anomalies in the shape effects observed in different field and laboratory investigations are probably caused by the different shape-sorting effects of particles moving by traction and by suspension. The readier transport of bladed pebbles can probably be explained by their observed “erratic saltation” type of motion, which tends to lift the bladed particles up into the flow, so that at sufficiently high fluid velocities their low settling velocity is more important than their poor rollability.
Bed Loading Movement at High Flow Intensities
As the flow intensity increases, and bed load becomes more abundant, the bed-load layer becomes thicker and the separation distance between bed-load particles becomes smaller. The difficulties of observing the details of particle motions in such thick, high-concentration bed-load layers become formidable— one might even say insurmountable. It seems fair to say that the ratio of hard observational data to theoretical deduction is probably lower in this area of sediment transport than in any other. The literature is replete with speculation about the forces and motions involved.
We start with the classic work of Bagnold (1954, 1956), which has played such an important role in subsequent thinking. Bagnold made pioneering experiments on interparticle forces in a strongly sheared mixture of water and solid particles. The experiments were made in a small, table-top apparatus that consisted of two concentric cylinders, with a thin annular space between. The inner cylinder was held stationary and the outer cylinder was rotated, giving almost uniform shear in the annular space, much like the hypothetical kitchen-table experiment described in Chapter 1. The annular space was filled with water containing a certain concentration of neutrally buoyant solid spherical particles. For a range of particle concentrations and rotation rates, Bagnold measured both the shear stress and the normal stress on the wall of the inner cylinder. He observed that both the normal stress and the shear stress were in excess of those for zero particle concentration, and he attributed these stresses, which he called dispersive stresses, to the intuitively reasonable effect of lateral forces engendered by particle interactions in the sheared mixture. Such interactions might be actual ballistic collisions, albeit cushioned to a greater or lesser degree by the ambient fluid, or they might only involve lateral particle motions caused by distortions of the local flow field by the presence of nearby particles moving at different speeds in the sheared medium.
It is easy to develop a dimensionless framework in which to evaluate the results of Bagnold’s experiments. Imagine that you are weightless, high above the Earth in a space station. You are equipped, somehow, to do the experiment described in Chapter 1, shearing a fluid between parallel plates, but without having to worry about leakage of fluid around the edges. You are at liberty to use particles of any density, because you do not have to be concerned that the particles will settle under their own weight or be centrifuged in a rotating device.
Which variables would govern the dispersive normal stress and dispersive shear stress of the kind that Bagnold observed in his experiments (Figure 10-9)? Plate spacing \(L\) and relative plate velocity \(V\) are not important by themselves but only in combination to give the shear rate \(V/L\); call that \(R\). The others are straightforward: density and viscosity of the fluid, and density, size, and concentration of the particles. You can nondimensionalize the stresses in a way similar to a particle Reynolds number: \((T / \rho)^{1 / 2} D / \mu\), and \((P / \rho)^{1 / 2} D / \mu\). One obvious independent dimensionless variable is \(\rho_{s}/\rho\) , the density ratio, and another is the concentration \(C\) itself, if it is taken to be a volume concentration. The third dimensionless variable needs to involve the shear rate; it is most natural to construct a variable in the form of a Reynolds number, \(\rho R D^{2} / \mu\).
Bagnold’s experiments were more restricted than your space-station experiment, because to avoid centrifugation he had to use neutrally buoyant particles. The implication of that is that the dispersive effects he found would have been even greater if \(\rho_{s}/ \rho\) could have been greater, as with natural sediment in water.
The dispersive stresses Bagnold observed are now known to be important in a wide range of what are called grain flows: flows of loose solid particles caused by the direct force of gravity, without the necessary involvement of a fluid medium. Grain flows are important in certain natural environments, as in snow avalanches, certain kinds of landslides, and, on small scales, sand flows down the lee faces of eolian sand dunes, and in technology as well.

Bagnold (1956) took the further step of applying the concept of dispersive stresses to what he called the “gravity-bed case”: a flow of fluid in a channel or conduit in a gravitational field, transporting denser particles near the bed, as what we would call, in the context of this chapter, bed load (Figure \(\PageIndex{5}\)). The idea is that if the flow is strong enough there can be a lowermost layer of transported sediment, with a thickness of many particle diameters, in which the shear is sufficiently strong that a dispersive normal stress makes its appearance and acts to maintain the bed-load layer in a dispersed state. Bagnold theorized that within this sheared and dispersed bed-load layer the fluid turbulence is unimportant, in the sense that it is not the principal agent that maintains the particles in the dispersed state. These ideas were later elaborated by Dzulynski and Sanders (1962), who applied the term traction carpet (which is in common use to this day; see, for example, Hiscott, 1994, 1995, and Sohn, 1995) to the concept, and by Moss (1972), who introduced the term rheological layer for essentially the same concept. A quotation from Moss (1972, p. 162) captures the essence of the phenomenon well:
As bed-load motion becomes more intense in sand-sized materials, a stage is reached wherein collisions between particles become inevitable and thereafter the load proceeds as a dense mass of colliding particles, buoyed up by the dispersive pressure thus generated.... This moving mass of particles behaves like a viscous fluid, but has a remarkably sharp boundary with the flow above and maintains almost constant thickness over quite large bed areas.... (It) will be called the “rheological layer.”
The problem is that although the concept of a dispersion layer is consistent with the well-established importance of dispersive stresses in certain ranges of shearing of particle–fluid mixtures, no one has ever seen inside one, owing to the obvious experimental difficulties. (One investigator—the writer of these notes!—once tried to overcome the observational difficulties by means of the seemingly ingenious technique of using monochromatic illumination of transparent sediment particles being transported in a concentrated bed-load layer by a transparent liquid with exactly the same index of refraction as the particles, in order to have a clear and unobstructed view of a few opaque fluid and sediment marker particles and record details of particle motions in the interior of the bed- load layer using high-speed cinematography. He could never get it to work well enough, though.) Until the importance of dispersive stress in concentrated bed- load layers is established by observation, rather than merely deduced, the concept is best regarded as hypothetical rather than as proven. Of course, traction carpets or rheological layers can still exist; it is just a matter of whether dispersive stresses or other effects like small-scale fluid turbulence are the more important factor in their dynamics.
Saltation in Water
In Chapter 11 you will learn that in the wind, saltation is the principal, and very characteristic, mode of particle movement. In saltation, particles take long, arching trajectories above the bed, little influenced by the turbulence in the flow. Here we address the question: What is the nature and relative importance of saltation in water? The importance of saltation in air is clear, but there is much less agreement on its importance in water. Saltating particle rise much higher above the bed in air (commonly a large fraction of a meter) than in water (only a few millimeters) because of the much greater effect of fluid drag and the reduced effect of particle inertia in water. Kalinske (1943) calculated that the height to which saltating particles would rise, for given particle size and shear velocity, should be inversely proportional to the fluid density, i.e., particles should rise \(800\) times higher in air than in water. Also, the criterion for suspension developed in a previous section, \(u_{*} = w\), implies that particles should be relatively easily taken into suspension in water, because of the much lower settling velocity of particles in water than in air. Therefore most engineering writers (Einstein, 1950; Einstein and Chien, 1955; Ippen, 1971; Vanoni, 1975) have assumed that suspension by turbulence is a much more important mechanism of sediment transport in rivers than saltation, even quite close to the bed. In contrast to this view, Bagnold (1956, 1973) has argued that true saltation is independent of turbulence, and that high concentrations of particles close to the bed tend to suppress turbulence and make saltation (and particle collisions) the dominant mechanism of sediment transport.
Certain observations by Gordon et al. (1972), Fernandez Luque (1974), Fernandez Luque and van Beek (1976), and Abbott and Francis (1977) suggest that simple ballistic movement of particles, and movement by particles impacting on the bottom, may not be as important in water as some authors have held. Gordon et al. (1972) studied the saltation of spheres of diameter \(6.6\) \(\mathrm{mm}\) and specific gravity \(1.3\) in a flow of water. Particle movement was made essentially two-dimensional by confining the flow within a flume only \(7.9\) \(\mathrm{mm}\) wide. Observed trajectories were typical of saltation except that take-off angles were rather low, generally in the range of \(10^{\circ}\) to \(35^{\circ}\). One reason for the low lift-off angle was that a saltating particle did not simply bounce off the loose particles on the bed; instead the moving particle rolled around the particle on the bed before lifting off to make another saltatory jump. There was a clear correlation between the fractional loss of kinetic energy and the angle of incidence in the collision, but the collisions were not simple elastic collisions; it seems clear that a combination of particle inertia and fluid drag forces was involved. Both Fernandez Luque (1974) and Abbott and Francis (1977), studying saltation in water, found that very few apparent saltations could be explained entirely as simple ballistic trajectories; some other kind of lift force was involved in most trajectories. These authors did not investigate Magnus effects, but it seems probable (particularly for the data reported by Francis) that the main lift was provided by turbulence. Abbott and Francis (1977, p. 253) found that “there appears to be an effective elastic rebound between the bed and a moving grain impinging on it.” Very few observed saltations immediately followed the return of a particle to the bed; most were preceded by some rolling. Furthermore, there seemed to be no difference in take- off velocity between particles rebounding from the bed and particles beginning a saltation from rest or rolling.
Murphy and Hooshiari (1982) studied the saltation of marbles \(15.7\) \(\mathrm{mm}\) in diameter on a bed of similar but fixed marbles. The settling velocity, about \(0.8\) \(\mathrm{m/s}\), was much higher than the shear velocities needed to produce continuous saltation (\(0.08–0.11\) \(\mathrm{m/s}\)), so there is no doubt that saltation rather than suspension was the dominant mode of movement. In this case, particles appeared to be rebounding directly from the bed, though the exact mechanism of initial rise from the bed could not be studied by the stroboscopic technique used. Analysis of the trajectories indicated that they could be satisfactorily accounted for by a model that took into account gravity (and buoyancy), horizontal and vertical components of drag, and the added-mass effect that is produced by accelerating a solid through a fluid (Hamilton and Courtney, 1977). Magnus effects were not significant for particles of this size and shape in water. The observations suggest that bed impact forces are sufficient to produce the upward rise, and that lift forces are not necessary. If this is true (and it is not proven, because the bed was rigid in the model, not loose as it would be in nature) then there is the possibility that saltation of larger (gravel-size) particles in water may be different from that of sand in water. It may be that the saltation of gravel in water is more like that of sand in air than that of sand in water.
All of the observations described above were made on flows in which very few particles were in saltation. Possibly fluid drag and lift play a much reduced role in initiating and maintaining saltation in a “traction carpet”, but the observations certainly suggest severe limitations on a simple impact hypothesis for saltation at low concentrations in water, and they indicate a very significant role for turbulence in transport of sand as bed load.


