Skip to main content
Geosciences LibreTexts

9.2.3: Hydraulic boundary conditions and geometric controls

  1. Last updated
  2. Save as PDF
  • Page ID
    16398

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    The hydraulic boundary conditions are crucial for determining the morphology of tidal basins and inlets. Not only is the relative dominance of waves or tides important, but other hydraulic conditions also control the morphodynamic behaviour. At the same time, the basin morphology has an influence back on the hydraulic conditions. Due to this feedback mechanism, the basin in essence determines its own evolution, although external conditions such as sediment availability and storm surges also play a role.

    The following geometric and hydraulic controls will be further explained in this chapter:

    1. The surface area of the basin, in combination with the tidal range, determine in principle the tidal prism (Intermezzo 9.3), the volume of water that has to flow in and out through the inlet during one tidal cycle (excluding any fresh water). For a short basin2, it is usually estimated by multiplying the mean surface area of the estuary by the mean tidal range in the estuary. This is only valid in the case of a negligible river discharge, since a river flow will also contribute to the filling of the basin. The tidal prism has empirically been found to determine the equilib- rium, or minimal stable cross-sectional channel area of an inlet (Sect. 9.5.2). The channel cross-sectional area and volume (Sect. 9.6.2) as well as the sand volume stored in the ebb delta (Sect. 9.4.3) have also been empirically related to the tidal prism;
    2. The morphologically active part of basins consists of deeper areas where the flow is concentrated during lower tidal water levels and of tidal flats that are covered during higher water and are exposed during lower water. Because of the different geometry (surface area, water depths) during low tide and high tide, the high tide propagates at a different phase speed (see Sect. 5.7.4) than the low tide. This can either strengthen or weaken the magnitude of the maximum flood flow compared to the maximum ebb flow (and thus shorten or lengthen the flood duration compared to the ebb duration). This leads to a net import or a net export of sediment respectively and hence steers the morphological development of the basin in time. The important controls for the tidal distortion are the surface areas at low and high water and the mean water depth at high and low water, both of which are determined by a combination of tidal range, channel depth and intertidal storage areas or flats (see Sect. 9.7.2);
    3. Tidal waves propagating into basins may be either progressive or standing, or a mixture of the two, depending on amongst others the length of the basin (see Sect. 5.7.3). The length of tidal basins is generally much shorter than the tidal wavelength. In short tidal basins the tidal wave is reflected and it has a standing character. The tidal range in the basin is of similar magnitude as on the open sea. In longer basins, resonance can occur when the basin length is approximately a quarter of the tidal wavelength (or a multiple of that). The tidal amplitude will then increase. The longer the basin the more the tidal wave is dampened by friction. The resulting weakening of the reflected wave, assures that the tidal wave has a stronger propagating character;
    4. In very short basins (length much smaller than the tidal resonance length), the combination of tidal range, channel depth and intertidal storage areas or flats results in a different type of asymmetry than asymmetry between ebb and flood duration (see under 2.). In the case of a short basin, the duration of the flow change is different at HW and at LW-slack (see Sect. 5.7.4). As we will discuss later this asymmetry is of great importance for the net transport of fine sediment in the basin (Sect. 9.7.3).

    Intermezzo 9.3 Tidal prism

    The tidal prism is defined as the volume of water entering a tidal basin during flood tide and leaving the basin again during ebb tide. Neglecting fresh water outflow, the tidal prism \(P\) is equal to half the time integral of the inflow and outflow during a tidal cycle:

    \[P = \dfrac{1}{2} \int_{0}^{T} |Q(t, 0)| dt\label{eq9.2.3.1}\]

    with \(Q(t, 0)\) the tidal discharge in the inlet of the basin.

    For a short basin the size of the basin is small compared to the tidal wave length, such that the spatial variation of the water level in the basin can be neglected (Sect. 5.7.3). From Eq. 5.7.3.15, we have \(Q(t, 0) = \partial \eta_0 /\partial t A_b\) with \(A_b\) the surface area of the basin. Herewith Eq. \(\ref{eq9.2.3.1}\) can be approximated as \(P = A_b H\). Therefore, the tidal prism is often estimated by multiplying the mean surface area of the basin by the mean tidal range \(H\) in the basin.

    For longer basins, the spatial variation of the water level in the basin cannot be neglected and the full Eq. \(\ref{eq9.2.3.1}\) must be computed. Also, for quite long basins the tidal wave may exhibit a (partly) standing wave pattern with nodes and antinodes in the surface elevation and discharge (Fig. 5.63). A node in the discharge at a particular location implies that no water is exchanged through that cross-section during the tidal cycle. As a consequence, only the part of the basin from the inlet to the antinode contributes to the tidal prism. An example is given in App. E.

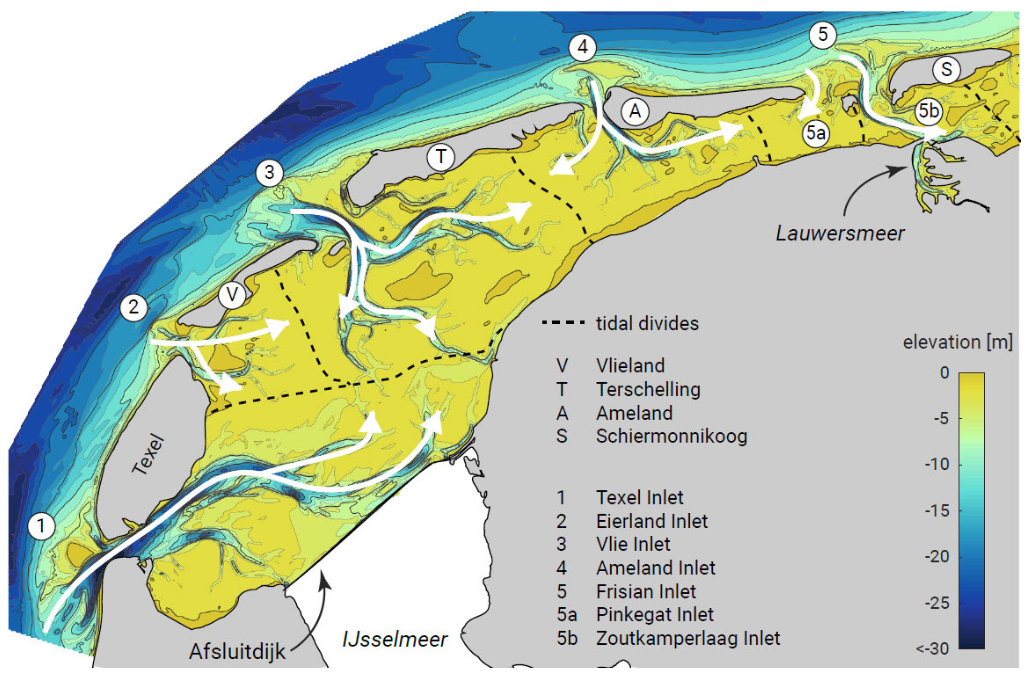
    截屏2021-11-25 下午8.39.40.png
    Figure 9.5: The Wadden Sea tidal dynamics model, displaying the types of tidal passes and the wantide zones. The movement of the tide on the North Sea is from left to right.

    Under calm conditions, a basin like the Wadden Sea can be thought to consist of multiple basins – each with their ‘own’ tidal prism – separated by tidal divides or watersheds (Fig. 9.5).

    2. Try to answer the following question: why is this method to estimate the tidal prism only appropriate for a short basin? See also Intermezzo 9.3 and App. E.

    This page titled 9.2.3: Hydraulic boundary conditions and geometric controls is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Judith Bosboom & Marcel J.F. Stive (TU Delft Open) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.