9.4.3: Empirical relationships: volume of the ebb-tidal delta
- Page ID
- 16404
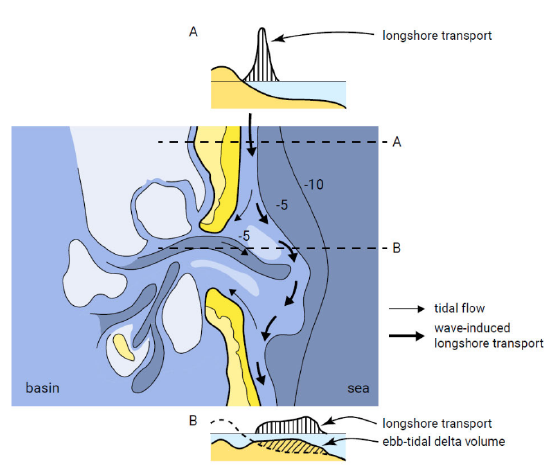
The great importance of the ebb-tidal delta is evident from the large volume of sand that is accumulated in this delta. This ebb-tidal delta volume (Fig. 9.20) will be larger for low onshore directed wave energy and large tidal forces. Under these circum- stances the ebb-tidal delta can extend far seawards without a distinct terminal lobe. Quite often the volume of sand deposited in an ebb-tidal delta is much larger than the total volume of the adjacent beaches. Although the governing physical processes (Sects. 9.4.1 and 9.4.2) are complex and not yet fully understood, it is beyond dispute that sediment exchange takes place between the adjacent barrier beaches and the ebbtidal delta.
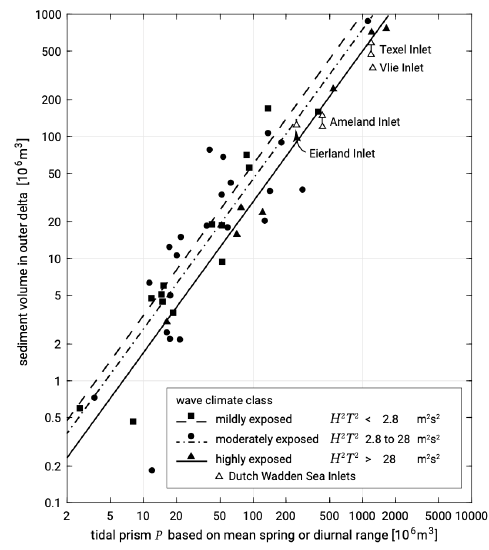
The volume of sand stored in the ebb-tidal delta has empirically been related to the tidal prism of the back-barrier system (Fig. 9.21). The relationship in Fig. 9.21 was first derived for outer deltas in the USA and reads:
\[V_{od} = C_{od} P^{1.23}\]
in which:
| \(V_{od}\) | sand volume stored in the outer delta | \(m^3\) |
| \(C_{od}\) | empirical coefficient | \(m^{-0.69}\) |
| \(P\) | tidal prism | \(m^3\) |
Figure 9.21 shows that the coefficient is dependent on the wave climate, in such a way that for the same tidal prism the volume in the ebb-tidal delta is smaller for more energetic waves. In Fig. 9.21 the tidal prism is determined based upon the spring or diurnal tidal range. Using the mean tidal prism \(P\) rather than the spring tidal prism, Eysink and Biegel (1992) found \(c_{od} = 63.3 \times 10^{-4}\) for the Wadden Sea (\(P_s /P \approx 1.15\)).
Even small changes in the tidal prism or the wave conditions (by nature or human interferences) may result in changes in the sand volume of the ebb-tidal delta. For example, suppose the tidal prism of an inlet is enlarged after flooding of part of the hinterland. According to the empirical relationships (Fig. 9.21), this will result in an enlargement of the volume of sand in the ebb-tidal delta. The sediment required for this enlargement may originate from the adjacent barrier coast, the back-barrier system (i.e. the basin) or from offshore. Most probably it will be a combination of these three sources, the distribution of which is very hard to determine without thorough knowledge of the underlying physics. Probably, erosion of tidal gullies will contribute most to the ‘sand demand’ of the (ebb) tidal delta, because of the relatively small morphological timescales of such adjustments (they are able to respond fast). Due to increased flow velocities, the tidal channels will (immediately) start to erode. The eroded material will mainly be deposited on the ebb-tidal delta where the flow decelerates. On the other hand, the contributions of the adjacent barrier coasts may be smaller but these coasts are more vulnerable as small changes in the sediment balance may cause severe coastline retreats.
Removal of sand from the outer delta
The sand in the outer delta may be used as a sand source for, say, beach nourishment or it may be necessary to dredge navigation channels through the outer delta. In both of these cases the sand is removed from the inlet system and the inlet will have been disturbed from the ‘equilibrium state’. Since the tidal prism and the protrusion rate of the delta remain constant, the supply of sand into the inlet via the flood channels does not change.
In the first years after the start of the dredging operations, the delta will retreat as a result of the sand loss, while the barrier islands are not affected. This trend reverses, however, as the outer delta will demand sand in order to return to its equilibrium state. Assuming that the inlet is a ‘closed system’, the demanded sand will be supplied by the adjacent coastlines, mainly by the downdrift coastline that will be cut-off from its supply. The erosion of the barrier islands will begin on the foreshore, the beach profile steepens and gradually the erosion of the beach will become evident. Since the erosion of the barrier islands occurs tens of years after the dredging, the cause of the erosion may not be linked to the dredging operation.
In order to minimise the additional erosion it may be wise to consider the option of dredging sand from the inner (flood-tide) delta instead of from the outer delta. If the amount of sand removed from the inlet system per year is less than or equal to the total volume of sand transported into the inlet per year via the flood channels, then the effects of dredging the inner and outer delta on the long term (decades to centuries) will be the same. However, the outer delta retreat and thus the additional erosion on the downdrift island will be slower in the case of dredging of the inner delta.
Effects of the construction of a groyne on the updrift island
The construction of a groyne on the updrift island will trap sediment that previously entered the inlet via the updrift flood channels. Not only can lee-side erosion be expected but erosion of the outer delta and the downdrift island as well. The outer delta acts as a buffer for the other elements of the inlet system. When sand is removed from one portion of the inlet the outer delta will respond by sharing sand with the other elements. This supply however is only a ‘short term loan’ which will be repaid by the adjacent coastlines in the longer term. So erosion of the outer delta can be expected to occur rapidly, while on the downdrift island this will take place after tens of years. In the case of a longer groyne, more sand will be trapped behind the groyne and it will also take more time before bypassing begins and consequently the erosion of the outer delta and the downdrift island will be more severe.