5.7.4: Tidal asymmetry
- Page ID
- 16338
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Sect. 5.3 it was described how wind waves propagating towards the shore become more and more asymmetric until the point of wave breaking. We had seen that this shoaling process was characterised by:
- increase in amplitudes;
- peaking of the wave crest and a flattening of the trough, and;
- relative steepening of the face resulting in a pitched-forward wave shape.
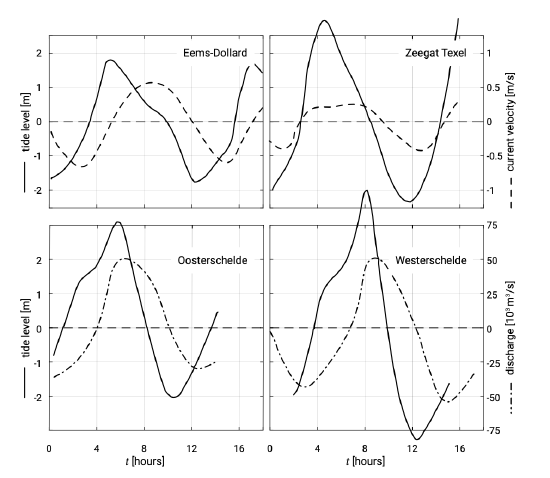
Comparable effects occur for tidal propagation in basins. This is illustrated in Fig. 5.65 for a number of tidal basins in the Netherlands.
As the tide propagates up the estuary, the water depth and basin width change. The shoaling and narrowing of the estuary slows the progress of the tidal wave, increasing its amplitude along the channel axis. Friction on the other hand will reduce the amplitudes. The net effect depends on the situation. Further, tidal asymmetry develops. As a result, in most tidal basins the tidal curves for water level and flow velocity (or discharge) strongly differ from a sinusoidal curve.
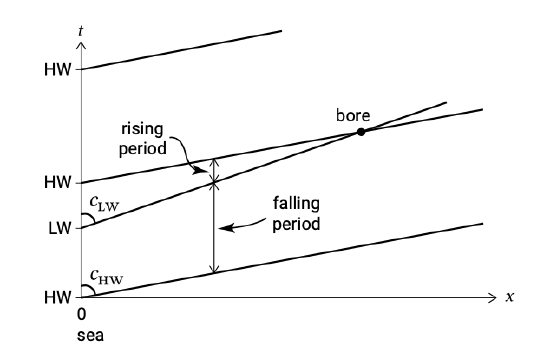
First consider the situation of a prismatic tidal river or basin without intertidal storage areas. We also neglect reflection from the head. In the absence of friction, the propagation velocity is given by \(c = \sqrt{gh} = \sqrt{g(h_0 + \eta)}\). We can also write the propagation velocity as \(c = \sqrt{gA_s/b}\). Without intertidal storage areas, the high and low tide use the same channels and the propagation velocity of the high tide \(c = \sqrt{g(h_0 + a)}\) is larger than of the low tide \(c = \sqrt{g(h_0 - a)}\). We can thus expect the rising period to be shorter than the falling period (see Fig. 5.66). Hence, the tidal wave becomes distorted, with a steep vertical face.
In extreme cases, as a result of certain bathymetric conditions, the steep vertical face can take on the form of a wall of water travelling up the basin. This causes an almost instantaneous rise of the water level as the water wall passes (see Fig. 5.66). This phenomenon is called a tidal bore (see Intermezzo 5.7). In the modelling of the surface in breaking waves often an analogy with a bore is made.
Friction gives an additional slowing down of the low tide with respect to the high tide, since the low tide ‘feels’ the bottom more. In tidal rivers this effect is even larger; since the river flow velocity and the tidal flow velocity are of similar order, the flow velocity and hence the friction is much larger at maximum ebb than at maximum flood.
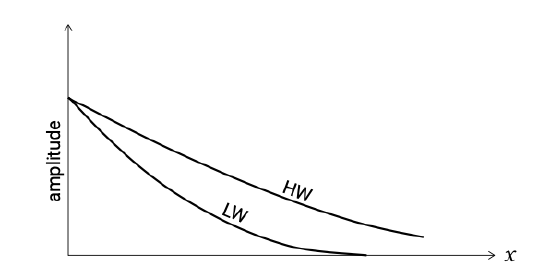
Friction also causes damping of the amplitude that is stronger during ebb around LW than during flood around HW. The preferential damping of the LW is depicted in Fig. 5.67. It results in an asymmetry of the surface elevation about the horizontal axis (a positively skewed signal).

Figure 5.68: Spectators watching the tidal bore in the Qiantang Estuary, China. Photo by Marcel J.F. Stive.

Figure 5.69: Tidal bore on the Nith River, Scotland. Photo by Richard P. Long.
Some rivers located at the landward end of an estuary experience an extreme tide-dependent condition - a tidal bore, an abrupt and migrating rise in the water level (Figs. 5.68 and 5.69). Tidal bores can cause great inconvenience to ship traffic. In those cases port authorities try and eradicate the bore by changing the shape and depth of the estuary.
Bores are uncommon, forming only in special circumstances that depend on tidal conditions and the morphology of the estuary. The bore in the Truro River of the Bay of Fundy is typically only about half a metre high. In the Bay of St. Malo on the northern coast of France, a bay with the world’s second largest tidal range, the bore rarely exceeds a metre in height. Large tidal bores occur in the Araguari River in the Amazon system and in the Qiantang estuary in China. The bore reaches \(5\ m\) in the Araguari River and nearly that height in the Qiantang. In the Brazilian Amazon tidal bores are known as pororoca.
Flood- and ebb-dominance
In the frictionless case and without reflection from the head, the vertical and horizontal tides are in phase. As a result, the horizontal tide displays similar saw-tooth asymmetry as the vertical tide. The flood duration is identical to the ebb duration and the ebb velocities are equal to the flood velocities.
Due to the effect of friction, we can expect a phase shift between vertical and horizontal tide that increases inland. In the extreme case of the horizontal tide leading the vertical tide by a phase difference of \(\pi /2\) (see Fig. 5.54), a shorter rising period directly corresponds to a shorter flood duration than ebb duration. In the absence of other nontidal forcing or river discharge, the net tide averaged discharge should be zero even though the tidal current is asymmetric. Therefore, a shorter flood duration means that the maximum flood velocities are higher than the maximum ebb velocities.
Systems in which the maximum flood velocities are higher than the maximum ebb velocities are called flood-dominant. If the maximum ebb velocities are higher, we speak about ebb-dominance. Flood-dominance can be expected for a large tide (or more precisely a large ratio of tidal amplitude over water depth \(a/h\)). In that case, the propagation of high water is faster than of low water and thus the rising period is shorter than the falling period. The result is higher velocity, shorter duration floods. This effect increases for longer basins.
Flood-dominance can be counteracted by the presence of a river flow that increases the seaward directed velocities (see Fig. 5.72). For negligible river flow, the presence of intertidal storage areas counteracts flood-dominance. In many tidal basins intertidal flats are present, which fall dry and are flooded again during the tidal cycle. The small water depths on these intertidal marshes and flats cause the high tide to propagate slower than the low tide. This is sometimes indicated by the ratio of intertidal storage volume over channel volume \(V_s/V_c\) (Friedrichs & Aubrey, 1988). Dronkers (1986, 2005) uses another indicator, viz. the wet surface area at HW over the wet surface area at LW: \(S_{HW}/S_{LW}\).
Ebb-dominance is further enhanced by the fact that the water level averaged over the flood period is generally higher than that averaged over the ebb period. Since during ebb the discharge is similar to the discharge during flood, the ebb velocities must on average be larger because of the smaller flow cross-section (for the same flood and ebb durations).
Summarizing, ebb-dominance means that the ebb has higher maximum velocities and a shorter duration than the flood, whereas flood dominance refers to higher velocity, shorter duration floods. A large tidal amplitude and shallow channels enhance flood-dominance. A large intertidal storage volume (as compared to channel volume) enhances ebb-dominance. This shows us that the basin geometry controls the tidal distortion.
Saw-tooth asymmetry of the horizontal tide
So far we mainly mentioned skewness (flood or ebb-dominance) of the horizontal tide. The horizontal tide can also display saw-tooth asymmetry. In the case of a short basin (length much smaller than a quarter of the tidal length, with the amplitudes of the incoming and reflected tidal wave of the same order) this will be the dominant form of asymmetry.
In a short basin, the tidal phase difference between seaward and landward end is negligible. Further, in a short basin \(\eta\) and \(u\) are out-of-phase; low water slack (flow reversal from ebb to flood) occurs at low water and high water slack (flow reversal from flood to ebb) occurs at high water. At slack water \(d\eta /dt = 0\). The rate of change of the velocity \(du/dt\) around slack water is proportional to the landward basin area \(A_b\) and inversely proportional to the channel cross-section \(A_s\) (this can be found using Eq. 5.7.3.15).
Consider a short basin with shallow channels and little storage-offering flats. The channel cross-section \(A_s\) is much larger around HW than at LW. As a consequence, the rate of velocity change at high water slack is smaller; the HW-slack duration is longer than the \(L_W\)-slack duration.
On the other hand, in a basin with vast storage-offering tidal flats and deep channels, Ab is much larger around HW than around LW. As a result the variation of the flow velocity around HW slack is much larger relative to LW slack; the HW-slack duration is shorter than the LW-slack duration.
Impact of the tide at sea
The asymmetry of the velocity variation in a tidal basin will strongly depend on the water level variation of the tide at sea. This holds especially for short basins, and to a lesser degree also for longer basins. A faster water level rise than fall at sea causes higher flood flow velocities than ebb flow velocities in the basin and vice versa. A long duration of HW at sea causes a long HW-slack water duration and a short duration of HW at sea a short HW-slack water duration. This holds in the same way for low water.
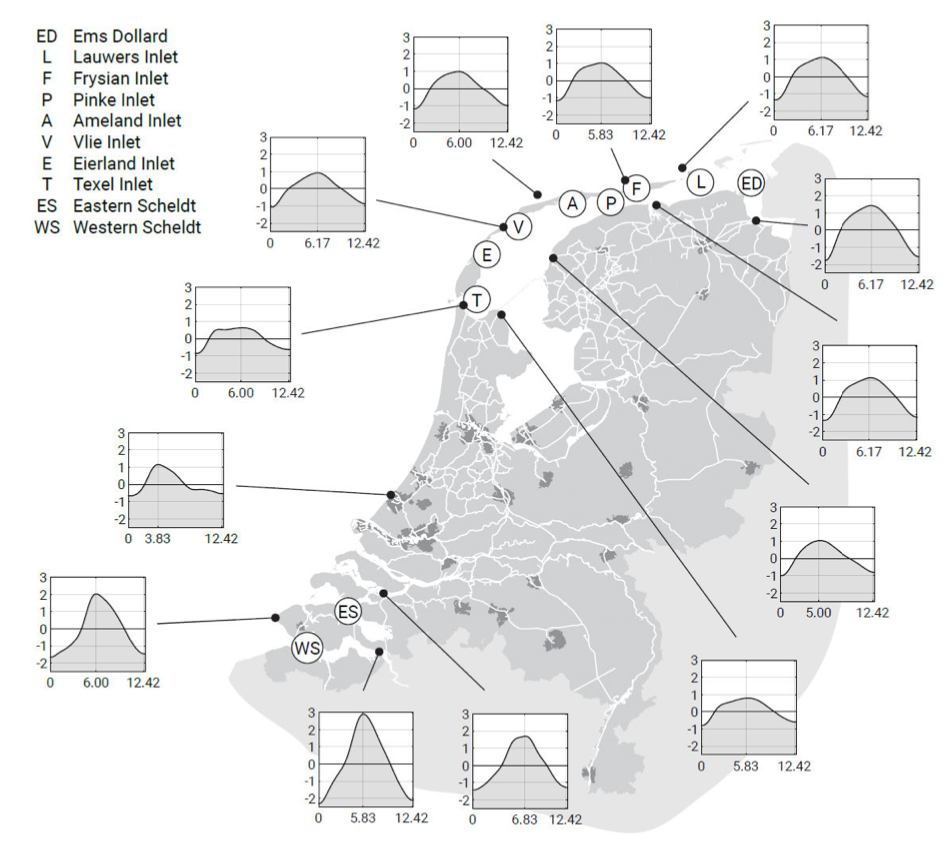
Deformation of the tidal wave along the coast has an impact on the ebb-flood asymmetry in the adjacent tidal basins and hence on the net inward or seaward sediment transport and the morphological evolution. Fig. 5.70 illustrates the tidal variation for the Dutch coast and the adjacent tidal basins; this shows how the sea-borne tidal asymmetry is transferred into the basins.
(Preview of) the relevance to sediment transport
The asymmetries of the horizontal tide are of extreme importance to the net sediment transport. The first type of asymmetry, skewness or asymmetry about the horizontal, is important for residual (net) sediment transport in tide-dominated areas (mainly tidal inlet systems). For instance, if the maximum flood velocity exceeds the ebb velocity, a residual sediment transport in the flood direction is likely to happen, since sediment transport responds non-linearly to the velocity. Hence, flood-dominance implies a residual transport in the flood direction. For medium to coarse sediment this is the dominant effect. Note that in the same way short-wave skewness in the nearshore (see Fig. 5.14) leads to a net transport in the wave propagation direction. Chapters 6, 7 and 9 pay due attention to transport due to skewness of the velocity signal in both wave- and tide-dominated environments.
Flood-dominant systems tend to import sediment (assuming the transport is a power function of the velocity, see Sect. 9.7.2). As a consequence, they tend to become shallower and their channels tend to infill. Ebb-dominance, on the other hand, results in a net seaward transport, which tends to keep channels deep. Ebb-dominant behaviour is an important driver for the formation of a tidal basin in coastal lowlands after a barrier breach. This is further treated in Sect. 9.7.2.
The second type of asymmetry (around the vertical) affects the residual transport for fine sediment in inlets and basins. This is because fines need time to settle; fine sediments are allowed to deposit if the slack duration is long enough. For asymmetries around the vertical, the slack durations are not equal; if for instance the duration of HW slack (before ebb) is longer than the duration of LW slack (before flood), stronger sedimentation occurs just before flow reversal to ebb. We will see in Sect. 9.7.3 that this leads to a net transport of fines in the flood direction.


