9.7.3: Fine sediment transport and siltation
- Page ID
- 16411
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For coarse sediment the bed load as well as the suspended load transport is determined largely by the hydrodynamic conditions and the sediment properties at the point of consideration. This can be modelled with a sediment transport formula (e.g. the Bijker or the Bailard formula, much like what we did in the previous section), or with an intra-wave model which describes the suspension process during a wave cycle (Ch. 6). In the case of fine sediment, the suspended sediment transport not only depends on the local instantaneous flow velocity but also on the flow conditions upstream and in the past. We therefore need to include a ‘memory effect’ that makes the sediment concentration at a certain point respond to the conditions in all points the suspended sediment has come through in the past (Sect. 6.8.1). The timescales of erosion and sedimentation become important, a characteristic that causes an essential difference in the tidal dynamics of fine sediment (silt) compared to coarser sediment (sand). For sand this timescale is an order-of-magnitude smaller than the tidal period (so that we can assume an instantaneous response), whereas for fine sediment the timescales are of similar order. For fine sediment we denote this timescale as \(T_{sed}\). If we assume that under the condition of a constant flow velocity after some time an equilibrium concentration \(c_{eq}\) is reached, then \(T_{sed}\) is the timescale for which the suspended concentration \(c\) approaches the equilibrium concentration. In formula form:
\[\dfrac{Dc}{Dt} = \dfrac{1}{T_{sed}} (c_{eq} - c)\]
Note that this is identical to Eq. 6.8.1.2. In principle a distinction must be made between the relaxation timescales \(T_{sed}\) for erosion and for sedimentation, respectively \(T_{Er}\) and \(T_{Se}\). The equilibrium concentration ceq can be determined experimentally; it appears often that
\[c_{eq} \approx \beta |u|^{n - 1}\label{eq9.7.3.2}\]
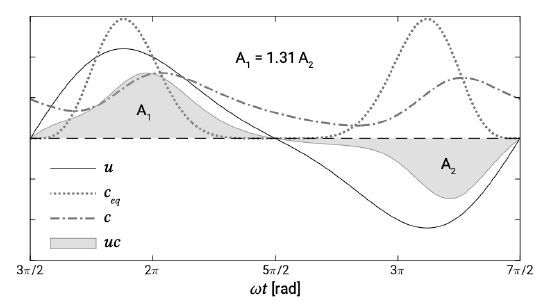
in which \(n = 3\) to 5 (depending on the type of sediment) and \(\beta\) a constant. Please note the resemblance between Eq. 9.7.2.1 and Eq. \(\ref{eq9.7.3.2}\). A (theoretical) example of the solution to this equation is shown in Fig. 9.32. The velocity signal \(u(t) = \cos (\omega t) + 1/4 \cos (2 \omega t - \varphi_{M4-2} = 3\pi /2)\) has been chosen such that the flood velocities are equal in magnitude to the ebb velocities. Hence, no residual bed load transport of coarse material will occur. For the equilibrium concentration, Eq. \(\ref{eq9.7.3.2}\) has been used with \(n = 5\), resulting in \(c_{eq} \propto u^4\). In the case of an instantaneous sediment response (coarser material), the concentration would be equal to the equilibrium concentration and the net suspended sediment transport would be zero. In the case of finer sediment, the sediment needs time to respond and will follow the red dotted line. This is computed from Eq. \(\ref{eq9.7.3.1}\) using \(T_{sed} /T_{M2} = 0.2\). It can be seen that now the concentration is generally higher during the flood period than during the ebb period. As a result the sediment flux \(uc\) during flood is 31% larger than during ebb leading to a net landward directed flux of fine sediment.
The asymmetry in the concentration stems from the asymmetry in the slack water periods. In the schematised situation of Fig. 9.32, the duration of high water slack (HW-slack, flow reversal from flood to ebb) is longer than the duration of low water slack (LW-slack, flow reversal from ebb to flood). Hence, a strong sedimentation occurs around HW-slack; in the initial ebb phase only little material is in suspension. Later in the ebb period more fine sediment is suspended. Around LW-slack part of this sediment settles, but not so much because of the short slack water duration. When the flood current increases in strength immediately a relatively large amount of suspended material is transported. Subsequently, the suspended concentration increases even further. It is clear that averaged over the flood, the concentration of suspended sediment is therefore larger than that during ebb. Over the whole tidal period, we therefore observe a net landward-directed transport.
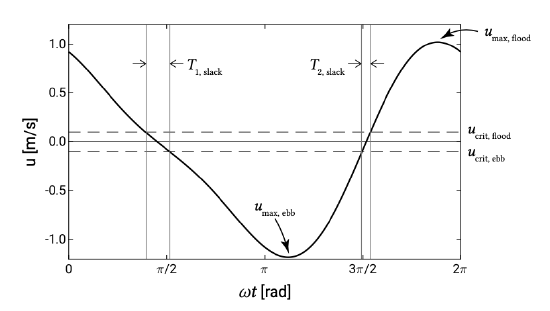
In practice, both types of tidal asymmetry can be present at the same time (Fig. 9.33). A short HW-slack and a net seaward-directed transport of fines, can be observed in Fig. 9.33. The slack durations before ebb (\(T_{\text{1,slack}}\)) and flood (\(T_{\text{2,slack}}\)) are defined by the flow velocity (\(u_{\text{crit,flood}}\), \(u_{\text{crit,ebb}}\)); for smaller velocity magnitudes sedimentation takes place. Since \(T_{\text{1,slack}} > T_{\text{2,slack}}\), an import of fines is likely to happen. For coarser sediment (sand) slack water duration does not play a role of importance because of the short sedimentation timescale. Generally speaking we may state that we have net flood transport for \(u_{\text{max,flood}} > u_{\text{max,ebb}}\), and net ebb transport in the reverse case. In the present example, the maximum ebb velocity is larger than the maximum flood velocity. Hence, an export of coarse sediment can be expected.
In Sect. 5.7.4 we discussed ‘Saw-tooth asymmetry of the horizontal tide’. We concluded that for a short basin with shallow channels and little storage-offering flats, the HW- slack duration is longer than the LW-slack duration. On the other hand, in a basin with vast storage-offering tidal flats and deep channels, the HW-slack duration is shorter than the LW-slack duration. This suggests that import of fines is a characteristic property of a tidal basin with shallow channels and limited tidal storage flats. Similarly, one may expect that basins with deep channels and large intertidal storage would be likely to export fines. However, the latter is often not true due to a counteracting effect that is especially important when large intertidal flats are present.
This counteracting effect is related to differences of sedimentation at HW and at LW. The relaxation timescale for sedimentation \(T_{Se}\) is amongst other factors dependent on the water depth, viz. \(T_{Se} \approx h/w_S\). Hence, the amount of sedimentation at HW can strongly differ from that at LW. This is particularly the case when the wet surface of the basin is much larger at HW than at LW (large intertidal storage), implying an on average smaller water depth at HW than at LW. The result is a larger sedimentation at HW than at LW, reducing the concentration and sediment flux during the ebb period.
Apparently, a large storage-offering flat area has two opposing effects on the net transport of fine sediment: on the one hand a large storage prism causes a short slack duration in the flow channel at HW-slack; on the other hand in this short period a strong settling can occur due to the small water depth. If the latter effect dominates this leads to a net import of fines, even in the case of large storage areas. This may be one of the reasons that many tidal basins are deposition areas for fine sediments (silt).
Further, wave stirring and storm surges can cause a strong erosion and export of fine sediment. Waves can be expected to stir up sediment very effectively and more so for smaller water depths. This increases fine sediment concentrations in the initial ebb phase enhancing an ebb-transport


