5.7.3: Tidal propagation into basins
- Page ID
- 16337
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In tidal basins we generally find a main channel, which transports the majority of the ebb and flood discharge. It is along this main channel that the tidal wave is primarily propagated. If we choose to align the \(x\)-axis with the channel-axis, we may approximate the tidal propagation with a set of one-dimensional equations. These are the balance equations for mass and momentum in the \(x\)-direction.
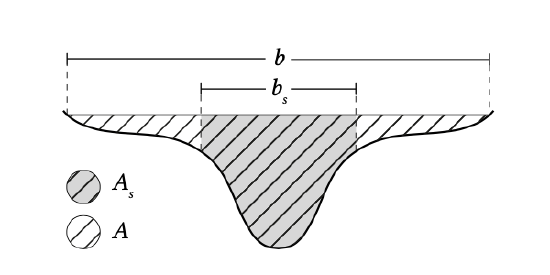
To derive these equations we schematise the cross-section \(A(x, t)\) of the basin with a width \(b\) into two parts. One part represents the flow carrying part of the cross-section, discharging all the flow, the other part is the storage part, which only stores water without discharging, see Fig. 5.61. The storage part represents the tidal flats that are covered during higher water and are exposed during lower water.
The flow-carrying cross-section has an area \(A_s (x, t)\), which is the product of a flow-carrying width \(b_s (x, t)\) and a representative instantaneous depth \(h(x, t)\). This depth \(h(x, t)\) is the sum of the representative flow-carrying water depth \(h_0(x, t)\) relative to a horizontal mean water level and the tidal level \(\eta (x, t)\). The mean flow velocity in the flow-carrying cross-section (averaged over the total cross-section) is indicated as \(u_s (x, t)\). The flow-carrying cross-section can be written as \(A_s = b_s h = b_s (h_0 + \eta)\). The tidal discharge through this cross-section is \(Q = A_s u_s\)
The one-dimensional balance equations are derived for an infinitesimal short section in the basin. The mass balance (continuity equation) yields:
\[\underbrace{\dfrac{\partial }{\partial x} (A_s u_s)}_{\text{volume change due to in- and outgoing transport}} + \underbrace{b \dfrac{\partial \eta}{\partial t} }_{\text{volume change due to water level change}} = 0 \Leftrightarrow \dfrac{1}{b} \dfrac{\partial}{\partial x} (b_s h u_s) + \dfrac{\partial \eta}{\partial t} = 0\label{eq5.7.3.1}\]
The mass balance equation can be simplified with \(b = b_s\) (no intertidal storage areas) and under the assumption of a prismatic channel (cross-sectional shape and size and bottom slope are constant along the channel, hence \(b\) is independent of \(x\)). This gives:
\[\dfrac{\partial}{\partial x} (hu) = \dfrac{\partial \eta}{\partial t} = 0\label{eq5.7.3.2}\]
Note that for convenience we have dropped the subscript \(s\) for \(u\). The total water depth can be taken outside of the \(x\)-derivative for a small ratio of tidal amplitude over water depth and a prismatic channel. Compare this equation to Eq. 3.8.3.3.
The momentum balance reads:
\[\underbrace{\dfrac{\partial }{\partial t}(A_s u_s)}_{\text{momentum change}} + \underbrace{\dfrac{\partial }{\partial x}(A_s u_s^2)}_{\text{in- and outflow of momentum}} + \underbrace{g A_s \dfrac{\partial \eta}{\partial x}}_{\text{pressure gradient}} + \underbrace{\dfrac{b_s}{\rho } \tau_0 = 0}_{\text{bottom friction}}\]
With \(b = b_s\) and under the assumption of a prismatic channel (so that \(A_s\) does not vary with \(x\)), we find the 1D shallow water tidal propagation expression:
\[\dfrac{\partial u}{\partial t} + u \dfrac{\partial u}{\partial x} + g \dfrac{\partial \eta}{\partial x} + \dfrac{\tau_b}{\rho h} = 0\]
Here, we have again dropped the subscript \(s\) for \(u\).
By conducting a scale analysis, it can be shown under what conditions which terms are of similar order of magnitude and which terms may be neglected. For characteristic orders of magnitude of the tidal amplitude to water depth ratio \(a/h = \mathcal{O} (10^{-1})\) and \(h \approx \mathcal{O} (10\ m)\) the advective (second) term on the left-hand side can be neglected.
For simplicity we assume a linear friction law \(\tau_b = \rho c_f |u| u \approx \rho r u\). We get:
\[\dfrac{\partial u}{\partial t} + g \dfrac{\partial \eta}{\partial x} + \dfrac{r}{h} u = 0\label{eq5.7.3.5}\]
Compare the above equation to Eqs. 3.8.3.1 and 3.8.3.2 and Eq. 5.7.2.1.
As in Intermezzo 3.5, we take the \(\partial /\partial t\) of the continuity equation (Eq. \(\ref{eq5.7.3.2}\)) and \(\partial /\partial x\) of the momentum equation (Eq. \(\ref{eq5.7.3.5}\)). For a small tide (\(a/h\) small) this leads to:
\[\dfrac{\partial^2 \eta}{\partial t^2} - gh \dfrac{\partial^2 \eta}{\partial x^2} + \dfrac{r}{h} \dfrac{\partial \eta}{\partial t} = 0\label{eq5.7.3.6}\]
This equation has elements of the classical wave equation (Eq. 3.8.1.4) and of a diffusion equation (last two terms of the left-hand side (LHS)).
We can implement further simplifications depending on the relative magnitude of the inertia (local acceleration) and friction term. In many shallow tidal basins, the flow is friction dominated. The inertia term may then be neglected to a first approximation.
Friction-dominated flow
Consider a shallow estuary for which friction dominates inertia. The basin is long, i.e. all tidal energy is dissipated in the basin before the tide reaches the end of the basin.
In a straight basin Eq. \(\ref{eq5.7.3.6}\) is valid. For friction-dominated flow, Eq. \(\ref{eq5.7.3.6}\) reduces to a diffusion equation (the last two terms remain):
\[\dfrac{\partial \eta}{\partial t} = D \dfrac{\partial^2 \eta}{\partial x^2}\]
in which \(D = gh^2/r\) is the tidal diffusion coefficient. The solution of this equation can be shown to be:
\[\eta (x, t) = ae^{-kx} \cos (\omega t - kx) \ \text{ with } \ k = \sqrt{\dfrac{\omega}{2D}}\]
From substitution in the continuity equation, Eq. \(\ref{eq5.7.3.2}\), we get:
\[u(x, t) = \dfrac{a}{h} \sqrt{\omega D} e^{-kx} \cos (\omega t - kx + \pi /4)\]
The amplitudes of the horizontal and vertical tide are progressively damped with distance \(x\) from the inlet. Furthermore, the velocity leads the surface elevation by 45°. The phase speed \(c = \omega /k\) is given by \(c = \omega /k = \sqrt{2 \omega D}\). Note that this differs from the phase speed of a linear progressive wave \(c = \omega /k = \sqrt{gh}\).
Note that with a quadratic friction law (instead of the simple linear approximation) the tidal diffusion coefficient is dependent on the flow magnitude and therefore varies strongly over the tidal period. This non-linear character implies that the basin deforms the tidal wave during diffusion and it loses its sinusoidal character. The symmetry between ebb and flood is broken.
Around slack water the flow will not be described correctly by the tidal diffusion equation; during the slack waters friction is not dominant, the tide then propagates approximately as an undamped wave (see the progressive wave solution of the classical wave equation of Intermezzo 3.5).
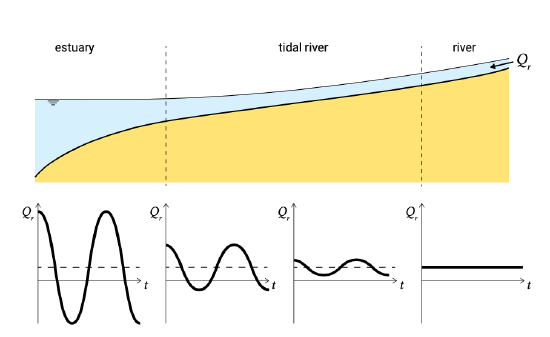
The Dutch former Zuiderzee is an example of a tidal basin of such length that the tidal wave at the end of the basin was nearly damped out. The tidal wave entering through the Texel Inlet or Marsdiep and the Vlie Inlet was largely damped out at Amsterdam and the Veluwe banks. Also in tidal rivers (where the river flow velocity and the tidal flow velocity are of similar order) we find slowly damping propagating tidal waves, e.g. the Lek and the Waal in the Netherlands and the St. Lawrence river in Canada. In these tidal rivers the reflected tidal wave is negligibly small, so that the tide has the character of an inland diffusing wave. See Fig. 5.62.
Inertia dominated flow
Let us now consider the (mostly unrealistic) case of negligible friction. Eq. \(\ref{eq5.7.3.6}\) reduces to the classical second order wave equation. We have already seen this equation when discussing tidal propagation in seas and ocean basins (Eq. 3.8.1.4). This equation allows wave propagation in two directions (in positive and negative direction along the channel axis). Since the incident tidal wave is not damped by friction, it is reflected at the basin end \(x = L_b\). The surface elevation at the inlet \(x = 0\) must be equal to a sinusoidal open sea or ocean tide \(\eta (0, t) = a \cos \omega t\). This results in a standing tidal wave:
\[\begin{array} {rcl} {\eta (x, t)} & = & {\dfrac{1}{2} \dfrac{a}{\cos k L_b} [\underbrace{\cos (\omega t - k(x - L_b))}_{\text{incident wave}} + \underbrace{\cos (\omega t + k(x - L_b))}_{\text{reflected wave}} ] =} \\ {} & = & {a \dfrac{\cos (k(L_b - x))}{\cos k L_b} \cos \omega t} \end{array}\label{eq5.7.3.10}\]
\[\begin{array} {rcl} {u (x, t)} & = & {\dfrac{1}{2} \dfrac{ac}{h \cos k L_b} [\cos (\omega t - k(x - L_b)) - \cos (k(x - L_b) +\omega t)] =} \\ {} & = & {-\dfrac{ac}{h} \dfrac{\sin (k(L_b - x))}{\cos k L_b} \sin \omega t} \end{array}\label{eq5.7.3.11}\]
In Eq. \(\ref{eq5.7.3.11}\) \(c\) is the phase speed \(c = \sqrt{gh}\). Water level and flow velocity are 90° out of phase, as can be seen from the terms \(\cos \omega t\) and \(\sin \omega t\) in Eqs. \(\ref{eq5.7.3.10}\) and \(\ref{eq5.7.3.11}\) respectively. This is an important characteristic of a standing wave pattern.
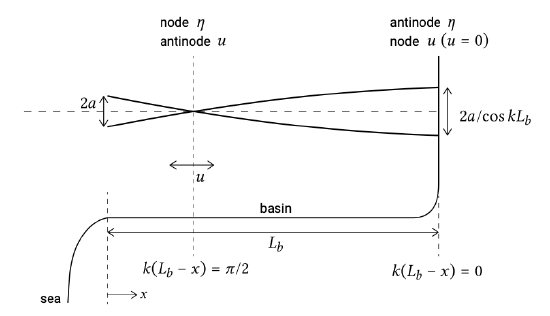
The amplitudes along a basin are sketched in Fig. 5.63. The amplitude of the tidal elevation along the estuary varies according to \(\cos (k (L_b - x)) = 0\). Hence, the standing wave has a maximum amplitude (or antinode) in the surface elevation at , i.e. at the landward end \(x = L_b\). The tidal amplitude at the landward end is therefore larger than that at the seaward end. The antinode in the surface elevation corresponds to a minimum (or node) in the velocity amplitude; at the landward end the velocity is zero. This can be seen from the term \(\sin (k(L_b - x)) = \pi /2\) in Eq. \(\ref{eq5.7.3.11}\).
If the basin is long enough, a node in the elevation (zero amplitude) and an antinode in the velocity (maximum amplitude) will occur for \(k(L_b - x) = \pi /2\). The longer the basin, the more nodes and antinodes it can accommodate.
The amplitudes of both the vertical and horizontal tide are inversely proportional to \(\cos kL_b\). If \(kL_b = \pi /2, 3\pi /2\), ..., then \(\cos kL_b = 0\) which means that the amplitudes of \(\eta\) and \(u\) become infinitely large. Note that \(kL_b = \pi /2\) is equivalent to \(L_b = 1/4 L\). So resonance occurs for basins with a basin length equal to a quarter of the tidal wavelength \(L\) or an uneven multiple of a quarter wavelength.
Resonance occurs because for \(kL_b = \pi /2\) the incident and reflected wave cancel each other at the mouth, or in other words we have a node of the surface elevation at the mouth. The amplitude of the vertical tide at the mouth is therefore zero relative to the amplitude in the basin. At the same time we had the condition that the tide at the mouth was equal to the ocean tide \(\eta (0, t) = a \cos \omega t\). Since this must be zero relative to the tide in the basin, the amplitude in the basin must go to infinity. In reality this would not occur, since bed friction would dampen the amplitudes.
So far, we considered a sinusoidal tidal motion and thus a single tidal frequency. In reality more tidal constituents are present. If the natural period of a basin is close to the period of one of the tidal constituents, that constituent will be amplified by resonance more than others.
Combination of friction and inertia
In most tidal basins both friction and inertia play a role. The tidal wave can be described as the superposition of an incoming and a reflected damped wave. Without friction a standing wave pattern will result. With friction, the incoming (and reflected) wave is partly damped so that the result is a total surface elevation pattern that has a partly propagating and partly standing character.

Figure 5.64 shows the ratio of the amplitude of a harmonic tidal component at the end of the basin over the amplitude at the mouth. Depicted is the solution of the 1D tidal propagation in a prismatic basin for various values of \(s_1 = r/h\omega\). Check from Eq. \(\ref{eq5.7.3.6}\) that \(s_1\) is the ratio between the friction term and the local acceleration term. For \(s_1 = r/h \omega = 0\) we recognize the frictionless situation with resonance for \(L_b = 1/4 L\) and \(3/4 L\). For large values of \(s_1\) the damping of the tide due to friction can be recognized. The values in between are a combination of both effects.
Width convergence and shoaling
So far we have only considered prismatic basins. In such basins, dissipation of energy due to friction inevitably dampens the tidal amplitude.
In the case of a funnel-shaped estuary, the cross-section is largest at the inlet and then gets progressively smaller. This gives a convergence of tidal energy that increases the tidal amplitude along the channel axis. The balance between the counteracting effects of energy loss due to friction and energy convergence due to width restriction, determines whether the tidal amplitudes increase or decrease along the channel axis. Note that a rapid convergence of energy for the incident wave implies a rapid divergence of energy for a reflected wave.
Progressive shallowing of a basin gives a similar concentration of wave energy counteracting the dampening by friction. The reason is that the propagation speed becomes smaller in smaller water depths. This is identical to the phenomenon of shoaling in wind waves (see Sect. 5.2.2).
In the case of gradual changes in width and depth (no reflection on the sides or on a sill) and in the absence of friction, the energy is conserved along the channel axis. Analogous to Eq. 5.2.3.2 we have:
\[Encb_s = \text{constant} \to \hat{\eta} \sqrt{gh} b_s = \text{constant} \to \dfrac{\hat{\eta}_2}{\hat{\eta}_1} \propto \left (\dfrac{h_1}{h_2} \right )^{1/4} \left (\dfrac{b_{s1}}{b_{s2}} \right )^{1/4} \]
According to this equation, width reduction has a stronger effect on the tidal amplitude than a depth reduction.
Storage considerations and short basins
A short basin has a length that is short relative to the tidal wave length: \(L_b \ll 1/4 L\), say \(L_b < 1/10 L\) or \(L_b < 1/20 L\). For such a short basin we can find a solution for the tidal elevation and velocity based on the continuity equation alone. Let us first look at the general continuity equation Eq. \(\ref{eq5.7.3.1}\). It can be written as:
\[-\dfrac{\partial Q}{\partial x} = b \dfrac{\partial \eta}{\partial t}\]
Integration along the channel axis from a location \(x\) to the end of the basin gives:
\[Q(t, x) = \int_{x}^{L_b} b \dfrac{\partial \eta}{\partial t} dx \label{eq5.7.3.13}\]
This equation shows that the tidal discharge in a certain cross-section depends on the amount of water needed to fill the basin landward of the cross-section under consideration. This volume of water (excluding any fresh water) that has to flow in and out through the inlet during one tidal cycle is called the tidal prism. It thus makes sense that the tidal prism has empirically been found to determine the equilibrium, or minimal stable cross-sectional channel area of a cross-section (Sect. 9.5.2).
In a short basin this situation can be simplified, since we can expect the water level in the basin to immediately follow the water level in the sea. There is no variation in the tidal amplitude along the channel axis: \(\partial \eta / \partial x = 0\). For a sinusoidal tide at the seaward boundary, the entire basin thus oscillates in exactly the same way at the first harmonic. Eq. \(\ref{eq5.7.3.13}\) then yields:
\[Q(t, x) = A_s u_s = \dfrac{\partial \eta_0}{\partial t} \int_{x}^{L_b} b dx = \dfrac{\partial \eta_0}{\partial t} A_b \Leftrightarrow\]
\[u_s (x, t) = \dfrac{\partial \eta_0}{\partial t} \dfrac{A_b}{A_s}\]
in which \(A_b\) is the basin surface area upstream of \(x\) and \(A_s\) is the channel cross- sectional area at \(x\). At the time of high water in the sea, everywhere in the basin the water levels are maximum. Low water also occurs everywhere at the same time. Therefore the velocities are zero at high and low water. At the time of mean water level, the ebb and flood currents are maximum. This corresponds with a velocity that leads the surface elevation (by \(\varphi = -\pi /2 = -90^{\circ}\)). The velocities in a cross-section are larger if a larger upstream surface area needs to be filled. Due to the uniformly oscillating water level, this situation is referred to as pumping mode.
In the case of a narrow gorge to the small basin, friction can reduce the amplitude inside the short basin and change the phase relationships.


