5.2.2: Shoaling
- Page ID
- 16319
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
Consider a linear (single harmonic) long-crested wave propagating in water that becomes gradually shallower (an alongshore uniform sandy coast with parallel depth contours). The wave is normally incident, viz. the wave crest is parallel to the depth contours, Fig. 5.2.
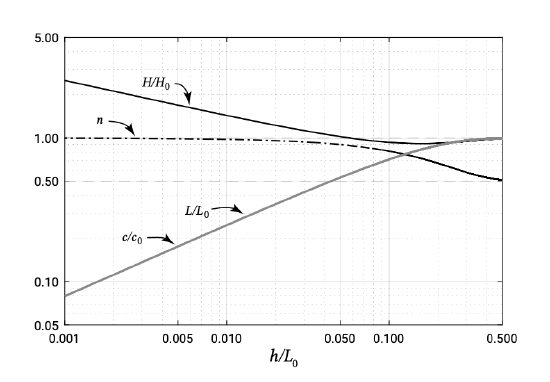
The wave propagation speed will be affected by the bottom when the water depth becomes less than about half the wavelength. A decreasing water depth yields a decreasing wave speed and wavelength according to the dispersion relationship as introduced in Sect. 3.5.2. Figure 5.3 shows \(c/c_0\) and \(L/L_0\) - where the subscript 0 refers to deep water conditions – as a function of local water depth \(h\) divided by \(L_0\). To find a relation between the wave height \(H\) and the water depth \(h\) we have to examine the energy balance. Outside the breaker zone the dissipation is approximately zero (neglecting bottom friction and white-capping) and integration of Eq. 5.2.1.3 yields:
\[U = Ec_g = Enc = \text{constant} \label{eq5.2.2.1}\]
where:
| \(U\) | wave power or energy flux per unit wave crest width (see also Eq. 3.5.3.4) | \(J/(ms)\) |
| \(E\) | wave energy per unit surface area | \(J/m^2\) |
| \(cg\) | wave group velocity | \(m/s\) |
| \(c\) | wave celerity | \(m/s\) |
| \(n\) | ratio \(c_g\) to \(c\) | - |
Eq. 3.5.3.3 and Fig. 5.3 show the dependency of \(n\) on the water depth and (deep water) wavelength. The energy flux \(U\) is also called the wave power and is the rate at which energy is transmitted in the direction of wave propagation across a vertical plane perpendicular to the direction of wave propagation and extending over the entire depth.
Since \(E = 1/8 \rho g H^2\), Eq. \(\ref{eq5.2.2.1}\) can be used to relate the wave heights at two arbitrary locations (locations 1 and 2):
\[U_2 = U_1 \to E_2 n_2 c_2 = E_1 n_1 c_1 \to H_2^2 n_2 c_2 = H_1^2 n_1 c_1 \]
or:
\[\dfrac{H_2}{H_1} = \sqrt{\dfrac{c_1}{c_2} \dfrac{n_1}{n_2}}\]
where the subscripts indicate the location at which the parameters are evaluated.
If we choose location 1 in deep water where the wave properties are more easily evaluated (\(n_1 = n_0 = 1/2\)), we find the following relationship for the wave height (subscripts 2 are dropped):
\[\dfrac{H}{H_0} = \sqrt{\dfrac{1}{\tanh kh} \dfrac{1}{2n}} = K_{sh}\label{eq5.2.2.4}\]
The parameter \(K_{sh}\) is called the shoaling factor and is purely a function of \(kh\) (\(n\) is a function of \(kh\) only). In Fig. 5.3 it is shown as a function of \(h/L_0\). It is 1.0 in deep water, then decreases slightly with water depth to 0.91 and subsequently rises to infinity. In reality the wave height increase in the shoaling zone is limited by dissipation due to wave breaking. Breaking and the limits of breaking are discussed a little later in this chapter. Note that the theory of shoaling is equally valid for decreasing as for increasing water depth. This means that a wave that passes over a local shoal resumes its original height, as long as no breaking has occurred.
In order to determine the shoaling coefficient, it may be helpful to use standard tables containing the values of the hyperbolic functions. These tables can be found in, for instance, the CEM (see Sect. 1.7.3). An extract of these tables is given in App. A.
Shoaling of tides and tsunamis
The phenomenon of shoaling has been explained in this section for wind waves. However, the intermediate and shallow water propagation of other waves such as tsunamis and tides is affected by depth-variations as well1. For example, at sea the wave heights of a tsunami are only of the order of a metre. When tsunamis travel into progressively shallower water, however, their energy is concentrated by shoaling and possibly tunnelling2, causing them to steepen and rise to many metres in height.
1. Note that shallow water is a relative measure depending on the wavelength of the wave; in Sect. 3.8.1 for instance, it was demonstrated that the oceans are already shallow water for the tidal wave.
2. Tunnelling is concentration of energy due to width restriction. See also Sect. 3.8.1 and Sect. 5.7 for examples.


