5.4.3: Wave boundary layer
- Page ID
- 16325
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)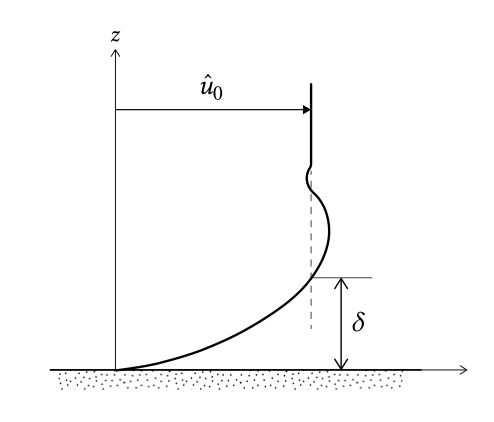
Most wave theories can be expected to be valid from the water level to a small distance from the bed (Fig. 5.23) where the flow still is unaffected by the boundary. Closer to the bed, in a thin layer called the wave boundary layer, vorticity (rotation) can be generated which is not included in the linear wave theory or in most other (irrotational) wave theories for that matter. The distance denoted as \(\delta\) in Fig. 5.23 is the thickness of the wave boundary layer, the transition layer between the bed and the layer of ‘normal’ oscillating flow. The thickness is generally between 1 cm and 10 cm for short period waves (\(T < 10 s\)). The reason for this small thickness is that there is not sufficient time for the layer to grow out in the vertical direction, because the current regularly reverses.
It is typical for oscillating boundary layers that the maximum flow velocity near the bed is somewhat larger (a few percent) than the so-called free stream velocity. The free-stream velocity amplitude \(\hat{u}_0\) according to linear theory is given by Eq. 5.4.1.1 for \(z = -h\):
\[\hat{u}_0 = \dfrac{\omega a}{\sinh kh}\]
The flow in the wave boundary layer is generally turbulent due to the presence of roughness elements on the bed. The water moving along the bed incurs a shear stress on the bed. This can be understood when imagining that – as a result of viscosity and turbulence – the flow sticks to the wall (no-slip condition). Hence, the orbital velocity increases from zero at the bed to the undisturbed free-stream velocity at the top of the wave boundary layer \(z = \delta\). Because of the thin boundary layer the velocity gradients perpendicular to the bed are large and give rise to large stresses in the wave boundary layer. The friction in the wave boundary layer results in dissipation of wave energy.
In coastal waters, turbulent stresses – arising from turbulent fluctuations of the velocity – are much larger than viscous stresses arising from small scale erratic movements of molecules. Now think of the total horizontal velocity \(u\) and vertical velocity \(w\) to be composed of a mean, a wave and a turbulent part, hence \(u = U + \tilde{u} + u'\) and \(w = W + \tilde{w} + w'\). Turbulent shear stress is defined as the stress introduced when averaging over the turbulent motion:
\[\tau (z) = \rho \overline{u' w'}\label{eq5.4.3.2}\]
The detailed modelling of the wave boundary layer is a complex research field. It involves the modelling of the turbulence in the wave boundary layer that is induced by roughness of the bed. Such a wave boundary layer model gives the detailed time-dependent velocity distribution over the wave boundary layer. Besides a purely oscillatory flow, a non-zero wave-averaged horizontal flow – called streaming – is found. It was first explained by Longuet-Higgins (1953) who demonstrated that for linear waves the streaming is directed in the wave propagation direction (see Fig. 5.26). It is therefore potentially important for transporting sediment onshore. The disturbance of the wave motion due to the wave boundary layer leads to additional stresses in the wave boundary layer when averaging over the organised wave motion. In analogy with Eq. \(\ref{eq5.4.3.2}\) these stresses are given by \(\rho \overline{\tilde{u} \tilde{w}}\) (the overbar now represents averaging over the short wave motion). Above the wave boundary layer this term can generally be neglected. In Intermezzo 5.5 it is shown that the term in the wave-averaged horizontal momentum equation responsible for the streaming is (proportional to) \(\partial \overline{\tilde{u} \tilde{w}} /\partial z\). It acts as a (depth-varying) force in the wave boundary layer pushing the flow forward. The expression found by Longuet-Higgins for the mean streaming velocity at the top of the boundary layer is:
\[U_0 = \dfrac{3}{4} \dfrac{\hat{u}_0^2}{c}\label{eq5.4.3.3}\]
For practical purposes it is generally enough to consider the following aspects of the wave boundary layer:
- The water moving along the bed incurs a shear stress on the bed. The orbital motion under waves, even without the presence of a uniform current, gives a time-varying shear stress at the bed, which can set sediment grains into motion (see Ch. 6);
- Due to the bed friction, the wave boundary layer dissipates energy from the flow above (this is the term \(D_f\) in Eq. 5.2.1.2);
- The wave-induced streaming (Eq. \(\ref{eq5.4.3.3}\)) should be taken into account for net-sediment transport computations.
In Sect. 5.5.6 it is briefly indicated how the vertical structure of the mean flow (including the wave boundary layer) can be resolved using a relatively simple eddy viscosity turbulence model. Until then we will only consider depth-integrated momentum equations that hence contain depth-invariant quantities. For instance, we consider the bed shear stress in a simple parameterised way, so that we do not have to bother with distributions of the shear stress over the depth.
Bed shear stress
If we refrain from turbulence modelling, (bed) friction is a major unknown that has to be determined using (empirical) friction laws. This introduces coefficients that need to be calibrated, which makes the calibration of these models important.
To determine the bed shear stress, Jonsson (1967) introduced the concept of a wave friction factor in analogy with the current friction factor (see Intermezzo 5.2). The current friction factor relates the bed shear stress to the depth averaged current velocity, whereas the wave friction factor relates the bed shear stress to the free stream velocity. For a current only, the magnitude of the bed shear stress is \(\tau_c = c_f \rho U^2\) (with flow aligned with \(x\)-axis, see Intermezzo 5.2). Under waves, the bed shear stress varies in time and reverses with the direction of the orbital velocities.
For linear waves with a free stream velocity \(u = \hat{u}_0 \cos \omega t\), Jonsson defined the friction factor \(f_w\) through the following expression for the magnitude of the maximum bed shear stress:
\[\hat{\tau}_w = 0.5 \rho f_w \hat{u}_0^2\]
For a rough bed and turbulent flow it is not easy to determine the friction coefficient as it cannot be measured directly. The friction coefficient will generally depend on the bed material and the bed forms (e.g. ripples). The following variables can be found in expressions for \(f_w\) for rough turbulent flow:
- the bed roughness \(k_s\) (Nikuradse roughness) or \(r\) of the wall; the bed roughness represents the size of the roughness elements, for instance the grains;
- the particle excursion amplitude close to the bed \(\hat{\xi}_0 = \hat{u}_0 /\omega\) (see Eq. 5.4.1.3 and App. A).
Assume a current only situation with the depth-mean flow velocity \(\vec{U} = (U, V)\) in the (\(x,y\))-direction. The bottom shear stress acts in the direction of the current and can be described by a quadratic friction law:
\[\tau_b = \rho c_f |\vec{U}| \vec{U}\]
The friction factor \(c_f\) is a dimensionless coefficient relating the bed shear stress to the square of the velocity. Linear friction laws are rarely used since they have no physical justification.
\(c_f\) can be expected to depend on the bed material and bed forms (bed roughness). For uniform flow in a canal driven by a small slope of the mean water surface, Chézy derived theoretically a Chézy coefficient \(C = 18 \log 12h/r\) where \(r\) is the bottom roughness and \(h\) is the water depth. The Chézy coefficient \(C\) relates to \(c_f\) as follows:
\[c_f = \dfrac{g}{C^2}\]
Alternatives are to prescribe a Nikuradse roughness height \(k_N\) or an empirical Manning value \(n\). The Nikuradse roughness and the Manning value can be related to \(c_f\). The choice between the methods affects the depth dependency of \(c_f\) and can therefore have important consequences for computed flow fields.
Let us consider two cases in which \(\hat{u}_0\) is the same, but \(T\) differs. For the case with a large value for \(T\), the value of \(\hat{\xi}_0\) is larger than in the case with the lower value for \(T\).
Assuming an equal value for \(r\), this means that the case with the larger value for the wave period gives lower values for the wave friction factor. This can be understood by considering that the boundary layer thickness varies with time. In the case of a larger wave period more time is available to develop the boundary layer that therefore reaches a larger maximum thickness. Consequently, the velocity gradients in the boundary layer are smaller leading to a smaller maximum shear stress and friction factor.
A frequently applied expression for \(f_w\) is that of Jonsson (1967), rewritten by Swart (1974) into:
\[f_w = \exp \left [-5.977 + 5.213 \left (\dfrac{\hat{\xi}_0}{r} \right )^{-0.194} \right ] \label{eq5.4.3.7}\]
\[f_w = 0.30 \ \ \ \text{ for} \left (\dfrac{\hat{\xi}_0}{r} \right ) < 1.59 \label{eq5.4.3.8}\]
Many simpler relationships exist such as (Soulsby, 1994):
\[f_w = 1.39 \left (\dfrac{\hat{\xi}_0}{r/30} \right )^{-0.52} \label{eq5.4.3.9}\]
\[f_{w, \max} = 0.3 \label{eq5.4.3.10}\]
For the roughness value \(r\) often the so-called Nikuradse roughness \(k_s\) is used, which is normally set as a function of the grain-size diameter.
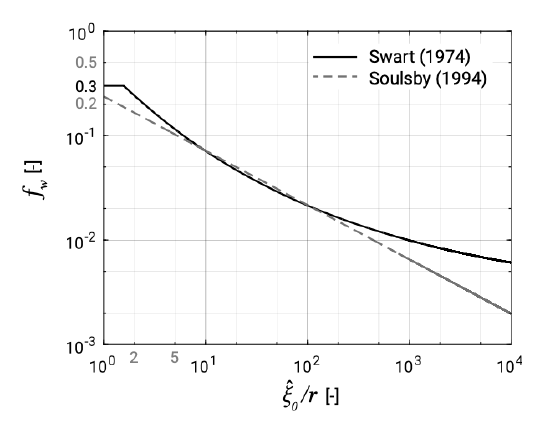
Equation \(\ref{eq5.4.3.7}\) and \(\ref{eq5.4.3.8}\) is shown graphically in Fig. 5.24 and compared to the simpler formulation of Eq. \(\ref{eq5.4.3.9}\) and \(\ref{eq5.4.3.10}\). As expected the friction factor \(f_w\) increases if \(\hat{\xi}_0 /r\) decreases. The upper limit of \(f_w\) has been questioned by various researchers: some suggest that there is no upper limit and that the friction factor remains proportional to \(\hat{\xi}_0 /r\).
In the case of irregular waves, the near-bed orbital velocity amplitude in the above expressions should be based on the root-mean-square wave height and the wave orbital excursion parameter near the bed on the root-mean-square wave height and peak period. Example 5.4.3.1 presents an example of a bed shear stress computation.
Input parameters
Water depth \(h = 3m\)
Roughness height \(r = 0.06 m\)
Wave height \(H = 1.18 m\)
Wave period \(T = 8 s\)
Required Bottom shear stress
Output The amplitude of the velocity near the bed can be found from linear wave theory:
\[\hat{u}_0 = \dfrac{\omega H}{2} \dfrac{1}{\sinh kh} = 1 m/s \ \text{ and }\ \hat{\xi}_0 = \dfrac{\hat{u}_0 T}{2\pi} 1.27m\]
For a value of \(\hat{\xi}_0 /r > 1.59\) the friction factor equals:
\[f_w = \exp \left [-5.977 + 5.213 (\hat{\xi}_0/r)^{-0.194} \right ] = 0.045\]
The maximum bottom shear stress follows from:
\[\hat{\tau}_w = \dfrac{1}{2} \rho f_w \hat{u}_0^2 = 22.5 N/m^2\]
Discussion For a maximum near bed orbital velocity of 1 \(m/s\) the bottom shear stress due to waves equals 22.5 \(N/m^2\). Now consider the situation of a mean current of 1 \(m/s\). Assume that the roughness height and water depth are the same as above. Using \(C = 18 \log 12h/r = 50 m^{1/2}/s\) we find:
\[\tau_c = \rho \dfrac{g}{C^2} U^2 = 3.9 N/m^2\]
The bed shear stress due to waves with a maximum near bed orbital velocity of 1 \(m/s\) is almost 6 times the value for the bed shear stress due to an average current velocity of 1 \(m/s\). This is a direct consequences of differences in boundary layer thickness and hence near-bed velocity gradients. The wave boundary layer is limited in thickness, whereas the current boundary layer generally occupies the entire water column.


