5.2.1: Energy balance

When waves propagate from deep into intermediate and shallow water depths, the waves transform, i.e. wave height, length and direction change until the waves finally break and lose their energy. Wave transformation takes place because the waves are affected by the seabed through processes such as refraction, shoaling, bottom friction and wave-breaking.

When the water depth becomes less than about half the wavelength (see Sect. 3.5.2 for deep and shallow water criteria), the waves start to be affected by the bottom and slow down. A certain harmonic component retains its frequency but the propagation speed \(c\) decreases through Eq. 3.5.2.2 and the wavelength \(L\) decreases correspondingly. The effect on the wave height can be imagined as follows: as the first wave in a wave train is slowed down due to decreasing water depth, the following wave is still at slightly deeper water and is thus moving at a higher speed. This wave tends to ‘catch up’ with the wave in front of it which is being slowed. This results in a concentration of wave energy and an increase in wave height. This process is called shoaling (Sect. 5.2.2). Changes in water depth and thus propagation speed can also occur along a wave crest. This forces an obliquely incident wave (at an angle with the coastline) to bend toward normal incidence (refraction, Sect. 5.2.3). Diffraction is wave transformation due to sheltering by obstructions like islands or breakwaters.

Various software packages are available to translate offshore wave conditions towards the near-shore. The effects of shoaling, refraction, bottom friction and wind can be incorporated in the models. Examples are HISWA and SWAN, both developed at Delft University of Technology. The simpler packages are based on for instance a spectrally integrated energy balance. (Numerically) solving the energy balance yields information on the wave transformation (i.e. the changes in \(H, L, c\) and wave direction \(\theta\)) of a wave field while the waves approach the shore. In the presence of a current, energy is not conserved any more, since transfer of energy between waves and currents is possible. In that case another wave quantity, wave action \(E/\omega\), will be conserved and the wave action balance rather than the energy balance should be solved. In the absence of a current, the wave action balance reduces to the energy balance. Since in these lecture notes the focus is on conceptual understanding, we will only consider the energy balance and treat a few simplified situations in which wave transformation is separated into the processes of shoaling, refraction, diffraction and breaking.

Integrating over all frequencies and directions in an irregular wave field, the following energy conservation equation can be composed:

\[\underbrace{\dfrac{\partial E}{\partial t}}_{\text{change of energy}} + \underbrace{\dfrac{\partial }{\partial x}(Ec_g \cos \theta)}_{\text{import of energy in } x\text{-direction}} + \underbrace{\dfrac{\partial }{\partial y}(Ec_g \sin \theta)}_{\text{and in } y\text{-direction}} = \underbrace{S - D}_{\text{gain of energy}}\]

Figure 5.1: Definition of wave angles for a wave propagating along a wave ray \(s\). The wave direction \(\theta\) is the angle with the \(x\)-axis. It generally differs from the (local) angle of incidence \(\varphi\) with respect to the depth contours. For a uniform coastline with the \(x\)-axis perpendicular to the coast we have \(\theta = \varphi\).

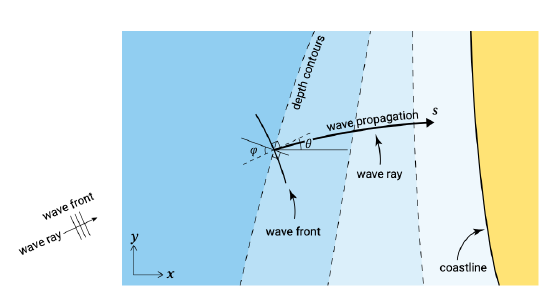
In this equation, \(\theta\) is the wave direction with respect to the \(x\)-axis (see Fig. 5.1), \(S\) is the generation term and \(D\) is the dissipation term. Underlying the spectral integration are the assumptions that: 1) the irregular wave field at one location can be represented by a single value for \(\theta\); and 2) that the total energy \(E = 1/8 \rho g H_{rms}^2\) is propagated at the wave group speed \(c_g\) (see Eq. 3.5.3.4). This only holds for a narrow-banded spectrum, and therefore not for a wide spectrum or a spectrum of combined swell and storm. For wave action conservation to reduce to energy conservation we must assume a spatially constant peak period.

The deep water group velocity is independent of the location and can therefore be taken outside of the derivative. In intermediate and shallow water, the group velocity is dependent on the location (the water depth) and can therefore not be taken outside of the derivative. \(S\) can be additional input of energy due to wind, which we generally neglect for the relatively small near-shore zone. Dissipation of wave energy \(D\) results in a decrease of wave height while waves approach the shore. Various processes can contribute to the dissipation term in the right hand side. The most efficient wave energy dissipation mechanism is wave breaking. This occurs mainly in the surf zone, but also in deeper water (where it is called white-capping). Other mechanisms include bottom friction – especially over large areas with shallow water – and interaction with vegetation (mangroves, salt marshes). \(D\) (and \(S\)) are not known well and all sorts of empirical formulations exist which allow for the equation to be solved.

If we assume that the wave conditions are stationary (do not change in time), the term \(\partial E/ \partial t\) in the left hand side equals zero and the energy balance in the coastal zone can be written as:

\[\dfrac{\partial}{\partial x} (Ec_g \cos \theta) + \dfrac{\partial}{\partial y} (Ec_g \sin \theta) = -D_f - D_w\label{eq5.2.1.2}\]

with the total wave energy \(E = 1/8 \rho g H_{rms}^2\) being propagated at the wave group speed \(c_g\) in the wave propagation direction \(\theta\). Wave dissipation due to wave breaking is denoted \(D_w\), and wave dissipation due to bottom friction is denoted \(D_f\). The direction \(\theta\) can change and we therefore need information on \(\theta\) to find a solution. For simple cases (alongshore uniform coast) Snell’s law gives this information (see Sect. 5.2.3). Eq. \(\ref{eq5.2.1.2}\) can also be written along a wave ray \(s\):

\[\dfrac{d}{ds} (Ec_g) = -D_f - Dw\]

Be aware that the wave ray is not a straight line due to \(\theta\) variations (see Fig. 5.1).

In order to close the equation, relations for \(D_f\) and \(D_w\) need to be formulated. \(D_f\) is a function of the shear stress due to (mainly) wave orbital motion near the bed (see Sect. 5.4.3) and is relatively small. Battjes and Janssen (1978) express \(D_w\) based on an analogy with a bore model from the observation that after breaking, waves behave like a bore or a moving hydraulic jump.