5.5.3: Wave-induced forces

The above equations describe the wave radiation stresses acting in a vertical plane of water. Horizontal gradients in the radiation stresses give rise to a net wave-induced force on the water in a particular direction.

Figure 5.31: Wave-induced forces. An increase of momentum transport (increase in radiation stress) in \(x\)- or \(y\)-direction is equivalent to a loss of momentum, hence, to exerting an opposite force on the water body.

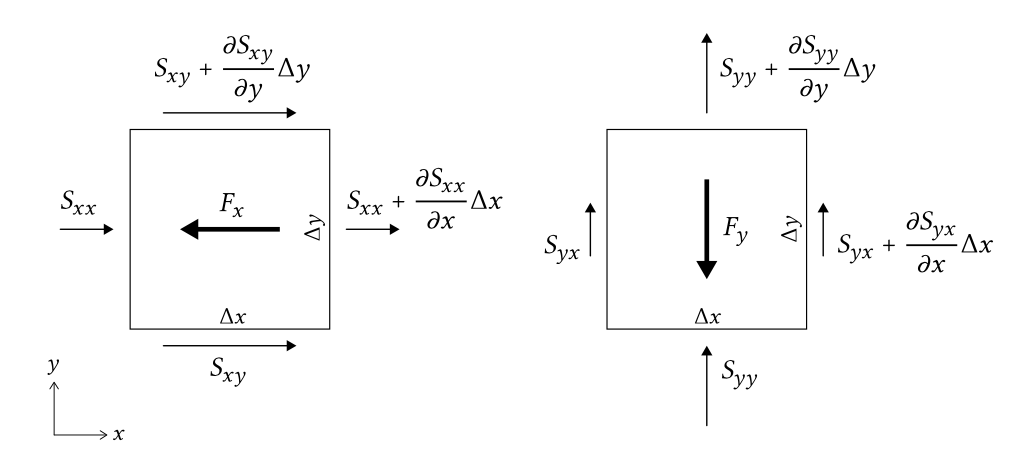
The net force in the \(x\)-direction is described by (Fig. 5.31):

\[F_x = -\left (\dfrac{\partial S_{xx}}{\partial x} + \dfrac{\partial S_{xy}}{\partial y} \right )\label{eq5.5.3.1}\]

where the first term represents the effect of variations in the \(x\)-directed radiation normal stresses and the second term the effect of variations in the \(y\)-direction of the \(x\)-directed radiation shear stress.

In coastal engineering practice, it is common to work with alongshore and cross-shore orientated axes. The \(y\)-axis is defined parallel to the shoreline, while the \(x\)-axis is perpendicular to the shoreline. \(F_x\) is thus the force in the cross-shore direction.

The second (shear) term in Eq. \(\ref{eq5.5.3.1}\) is zero for an alongshore uniform coastline (no gradients in the \(y\)-direction). We then have:

\[F_x = -\dfrac{dS_{xx}}{dx} \ \ \text{ for an alongshore uniform coast}\]

In the alongshore direction the force is:

\[F_y = -\left (\dfrac{\partial S_{yy}}{\partial y} + \dfrac{\partial S_{yx}}{\partial x} \right ) \label{eq5.5.3.3}\]

The first term in Eq. \(\ref{eq5.5.3.3}\) can be non-zero if gradients in wave height occur along the coast. For an alongshore uniform coast this term is zero such that Eq. \(\ref{eq5.5.3.3}\) reduces to:

\[F_y = -\dfrac{dS_{yx}}{dx} \ \ \text{ for an alongshore uniform coast}\label{eq5.5.3.4}\]

Remember that \(S_{yx}\) - the radiation shear stress on a plane perpendicular to the \(x\)-axis – represents the transport of \(y\)-momentum in the \(x\)-direction. A cross-shore gradient herein gives a net force in the \(y\)-direction.

Variations in the radiation stresses occur due to changes in \(n, E\) or \(\theta\). Further offshore the wave-induced forces are relatively small, but in the nearshore zone large forces occur due to wave transformation as a result of large gradients in water depth.

In the shoaling region the wave height and hence wave energy increase up to the edge of the surf zone, from where the wave height and wave energy decrease again. In the shoaling region the value of \(n\) gradually increases from its deep water value \(n = 1/2\), to its shallow water value \(n = 1\). The wave angle \(\theta\) gradually decreases from deep water to shallow water. The combined result is a positive gradient of \(\partial S_{xx}/\partial x\) and an offshore directed force in the shoaling region, and a negative gradient of \(\partial S_{xx} /\partial x\) and an onshore directed force in the surf zone. Section 5.5.4 shows how this results in wave set-down in the shoaling region and wave set-up in the surf zone. We will further see that the force in the \(y\)-direction is zero outside the surf zone but non-zero in the surf zone where it drives a longshore current. It is of course only present in situations where the waves approach the coastline under a certain angle (such that there is a component of the wave orbital velocity in the alongshore direction).

We have expressed the depth-integrated wave forces in terms of the radiation stresses, which is quite common in coastal engineering applications. Other equivalent expressions can also be found in model descriptions (Intermezzo 5.5).

Intermezzo 5.5 Wave forces in momentum equations

In momentum equations that are averaged over the wave motion, wave forces appear. These wave forces have two contributions: due to pressure fluctuations and due to momentum transfer by the particle velocity. They may be formulated in terms of radiation stresses (as in Eq. \(\ref{eq5.5.3.1}\)-Eq. \(\ref{eq5.5.3.4}\)) or they may equivalently be expressed in terms of the wave orbital motion and wave-induced pressure. In the latter case the wave forces in three dimensions may be expressed as:

\[\dfrac{R_x}{\rho} = -\dfrac{\partial \langle \tilde{u}_x \tilde{u}_x \rangle}{\partial x} - \dfrac{\partial \langle \tilde{u}_y \tilde{u}_x \rangle}{\partial y} - \dfrac{\partial \langle \tilde{w} \tilde{u}_x \rangle}{\partial z} - \dfrac{1}{\rho} \dfrac{\partial \langle p_{\text{wave}} \rangle}{\partial x}\label{eq5.5.3.5}\]

\[\dfrac{R_y}{\rho} = -\dfrac{\partial \langle \tilde{u}_x \tilde{u}_y \rangle}{\partial x} - \dfrac{\partial \langle \tilde{u}_y \tilde{u}_y \rangle}{\partial y} - \dfrac{\partial \langle \tilde{w} \tilde{u}_y \rangle}{\partial z} - \dfrac{1}{\rho} \dfrac{\partial \langle p_{\text{wave}} \rangle}{\partial y}\label{eq5.5.3.6}\]

\[\dfrac{R_z}{\rho} = -\dfrac{\partial \langle \tilde{u}_x \tilde{w} \rangle}{\partial x} - \dfrac{\partial \langle \tilde{u}_y \tilde{w} \rangle}{\partial y} - \dfrac{\partial \langle \tilde{w} \tilde{w} \rangle}{\partial z} - \dfrac{1}{\rho} \dfrac{\partial \langle p_{\text{wave}} \rangle}{\partial z}\label{eq5.5.3.7}\]

Note that the wave forces \(R_i\) are not integrated over the depth. The brackets \(\langle \ \rangle\) denote time-averaging over the short wave period. The wave orbital motion is now denoted with (\(\tilde{u}_x, \tilde{u}_y, \tilde{w}\)), with the tilde to distinguish the wave motion from the mean motion. Note the pressure contribution due to the non-zero time-averaged wave pressure and the horizontal momentum transfer terms in \(R_x\) and \(R_y\) that are directly related to the radiation stresses. In \(R_z\) we recognise the term \(-\rho \overline{\tilde{w}^2}\) that contributed to Eq. \(\ref{eq5.5.3.5}\), \(\ref{eq5.5.3.6}\) and \(\ref{eq5.5.3.7}\). We can also recognise the term \(\partial \langle \tilde{u} \tilde{w} \rangle /\partial z\) that was said to act, in the wave boundary layer, as a horizontal force pushing the flow forward (causing streaming, Sect. 5.4.3).