7.3.2: Beach states
- Page ID
- 16374
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let us first investigate morphologic features that we may encounter on the upper shoreface on the timescale of wave events (short term variation). Remember that we defined the upper shoreface to range from the surf zone at its furthest offshore reach (i.e. the active depth as defined by Hallermeier) to the first dune or cliff face. Part of the upper shoreface are the beach (normally sub-aerial) and the intertidal zone, which is the zone between low water and high water, at the transition between the surf zone and the beach.

Looking at the intertidal zone, we observe strongly three-dimensional morphology, probably the strongest of the upper shoreface. An example is shown in Fig. 7.9, where we observe a ridge-runnel structure on the intertidal beach. Although it impacts beach recreation and use, the importance of ridge-runnel structures in terms of shoreface behaviour is limited. We expect that the surf zone morphological structure has a larger impact on upper shoreface behaviour. On many beaches worldwide we may observe one or two and sometimes more surf zone bars, while in the intertidal zone a bar may also be present. In the examples presented on the Holland coast (a so-called dissipative beach, see later on in this section) we observe one surf zone bar and an intertidal bar. The bars determine the locations and rates of energy dissipation due to wave breaking and may thus dictate the morphological response. Further on, we will discuss the many years averaged behaviour of the surf zone bars, which determines their cross- shore location (Sect. 7.3.4).
On the timescale of wave events, we may observe highly dynamic variations of the upper shoreface profile and plan form. In the literature, the various morphodynamic regimes (also called beach states) have been classified according to their overall appearance, which is often related to previous weather conditions on daily to monthly timescales. Wright and Short (1984) distinguished a series of six beach states that are ranked hierarchically from the highest state, dissipative, to the lowest state, reflective.
In between the two ends, four intermediate beach states can be discerned. They based their analysis on observed behaviour at Australian beaches. Dissipative and reflective beaches are relatively two-dimensional, although reflective beaches usually have pronounced arc-shaped shoreline formations that are called beach cusps. Due to their small alongshore variability, the dissipative and reflective end members in the beach state sequence can be characterised by their cross-shore profile. The cross-shore profiles of reflective and dissipative beaches correspond roughly to ‘summer’ and ‘winter’ beaches, respectively (see Fig. 1.3 and Sect. 7.3.3). They can be described as follows:
Reflective beaches are characterised by a relatively steep and narrow beach face with a berm and a narrow surf zone without bars. Nearshore and beach slopes are between 0.10 and 0.20. The sandy material is relatively coarse (see Sect. 7.2.2). For these beaches a large Iribarren parameter (Eq. 5.2.5.5) can be expected (say larger than 2). Collapsing or surging breakers are common on reflective beaches. The corresponding waves have a low steepness (long and small amplitude waves). Thus, reflective beaches are the result of a period of mild wave conditions that transport sediment onshore. Reflective beaches are often found in swell and monsoon wave climates (see Sects. 4.3.2 and 4.3.3). Since in these climates the conditions have a low variability, the resulting morphodynamic behaviour is less dynamic than is the case for storm wave climates that are characterised by a higher variability.
Dissipative beaches – at the other end of the spectrum – are characterised by a wide and flat sandy coastal zone with one or multiple linear bars and with dunes backing a wide beach. The nearshore slope is about 0.01 and the beach slope about 0.03. The sandy material is relatively fine. The corresponding Iribarren numbers are small (around 0.2 to 0.3, corresponding to spilling breakers). A dissipative beach is the result of high energy waves that start breaking far offshore (wide surf zone, say up to 500 m wide). These high energy and short waves are typical for a storm wave climate and the associated variability results in a highly dynamic coastal profile.
The four intermediate beach states are all strongly three-dimensional. Whereas rip currents (Sect. 5.5.7) and corresponding rip channels are generally absent on pure dissipative and reflective beaches, they are an important attribute of intermediate beach morphologies. For intermediate beach states, plunging waves tend to occur.
Instead of the Iribarren number, another more or less equivalent parameter is often used to indicate the beach state, viz. the dimensionless fall velocity:
\[\Omega = \dfrac{H_b}{w_s T}\]
where \(H_b\) is the wave height at breaking, \(T\) is the wave period and \(w_s\) is the fall velocity. The reflective beaches at the one end of the spectrum typically have \(\Omega < 1\), whereas for dissipative beaches at the other end of the spectrum we would have \(\Omega > 6\). For values in between intermediate beach states are found.
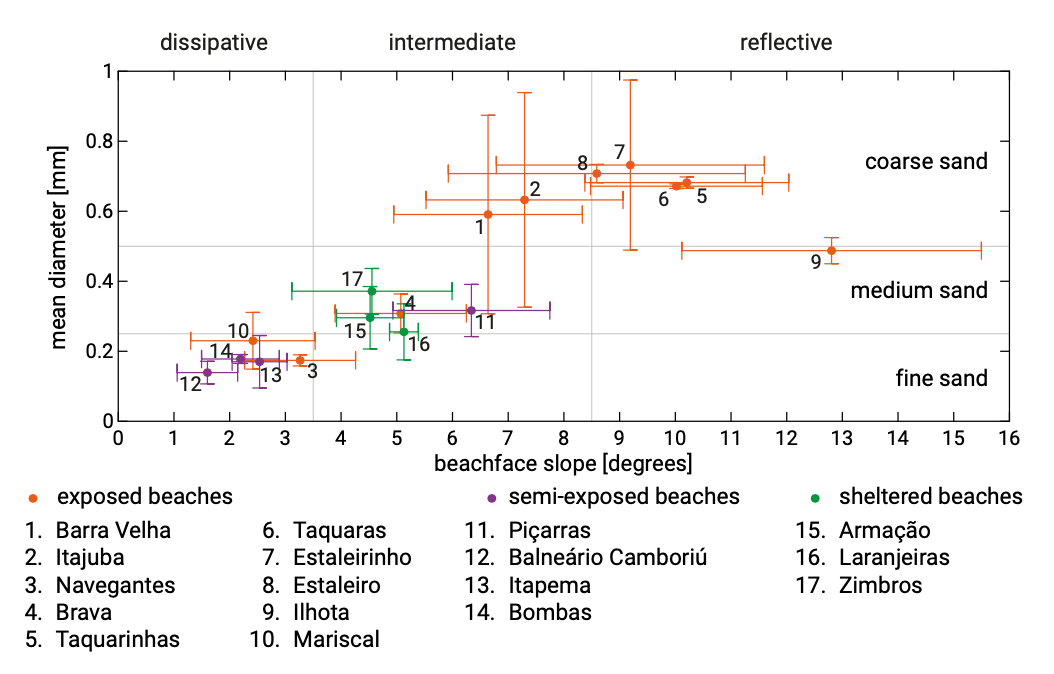
Klein et al. (2005) used the above explained distinction between dissipative, intermediate and reflective to classify southern Brazilian beaches (Fig. 7.10). Their work is very illustrative in showing the dependency on grain size and beach face slope.
The beach state at a certain location is not invariable; beaches can move through a series of beach states. Wright and Short (1984) use the dimensionless fall velocity to explain whether the response will be slow (low energy, reflective) or fast (high energy, dissipative) and whether erosion or accretion will occur. Mild wave conditions slowly force a beach towards a reflective beach state through onshore sediment transport, whereas storm waves are responsible for fast offshore movement of sediment resulting in a dissipative beach state. Hence, wave conditions which move a beach toward a higher state (the dissipative state being the highest in rank) cause erosion and wave conditions which move a beach downstate2 cause accretion.

Based on ARGUS video imaging techniques Lippmann and Holman (1990) and Ranasinghe et al. (2004) gained detailed insight into intermediate beach state dynamics at two different single barred beaches: Duck, North Carolina, USA and Palm Beach, Sydney, Australia, respectively. These studies showed that beaches continuously cycle through the four intermediate beach states in response to changing wave conditions. The three-dimensional structure of the morphology can be wiped out by an episodic event (a reset event, a high energy event that resets the three-dimensional character to an alongshore uniform bar position characteristic of the highest beach state). In conclusion, we may encounter high three-dimensional variability, which may turn into two-dimensional variability (alongshore uniform morphology) after a reset event (Stive & Reniers, 2003), see also Fig. 7.11). The progression from alongshore uniform morphology to the reflective beach takes place in weeks or months.
Depending on the beach state, rhythmicity can be observed in for instance beach cusps and rip channels3. Scientists have long tried to couple the spatial scales of these rhythmic features to certain length scales in the hydrodynamic forcing or geological constraints. However, in the last two decades or so, the focus has been more and more on self-organisation (see e.g. Coco and Murray (2007)). Self-organisation means that certain spatial patterns are associated with internal dynamics rather than with external forcings. These two contrasting approaches are further explained in Intermezzo 7.2.
Obviously, we have discussed interesting notions about intertidal and surf zone variability due to antecedent and concurrent forcing conditions. With timescales of antecedent forcing conditions of days to months, these observations are of importance for the beach state and its suitability for recreation and beach use, but are of limited importance on longer timescales.
Traditionally, it has been assumed that the spatial structures in the forcing (called forcing templates) become imprinted in the sediment bed. Observed length scales in the resulting morphology would then correspond directly to length scales in the forcing. A complicating factor is that the morphodynamic response is not always instantaneous. This implies that some time would be required for the spatial scales of the morphological patterns to evolve towards the scales of the forcing. Due to natural variability in the forcing, not enough time may be available to get to that point. Hence, the morphology of the system generally reflects the mix of the antecedent and concurrent hydrodynamics (thus a history of wave height, period and direction combinations). Predictability of the morphological length scales then strongly depends on the knowledge about the entire history of the forcing and – if only the concurrent forcing is known – on the relative importance of antecedent and concurrent forcing. Note that due to the stochastic nature of the hydrodynamic forcing conditions, the future forcing is at best known in statistical terms!
In a self-organisation approach it is assumed that rhythmic features are initiated by positive feedbacks between hydrodynamics and morphology (leading to divergent behaviour) and are stabilised by negative feedbacks (leading to convergent behaviour), see Sect. 1.5.2. This implies that the observed length scales in the coastal morphology do not necessarily correspond to the length scales of the initial forcing processes. Only after a feedback process between forcing and morphology do certain length scales predominate. To differentiate it from forced behaviour, self organisation has also been termed free behaviour.
Note that although length scales of the morphodynamic features do not match those of the external forcing, self-organisation approaches assume the system to respond to (changing) hydrodynamic forcing. This is in accordance with observations that when hydrodynamic conditions change, bars and other features respond. The self-organisational processes, in which certain length scales prevail, need sufficient time for the dominant length scales to appear (hence the concurrent forcing should last sufficiently long).
Let us consider the example of rip-channel spacings in alongshore non-uniform surf zone bars (generally in the order of 100s of metres). A once popular explanation of rip channel spacing being related to length scales in the forcing, was forcing due to edge waves. Edge waves are waves trapped against a shoaling beach. They are the wind-wave equivalent of coastally trapped tidal Kelvin waves (Sect. 3.8.3). Just as with Kelvin waves, the amplitude of edge waves varies sinusoidally along the shore and diminishes rapidly seawards from the shoreline. Whereas Coriolis was the mechanism behind the Kelvin waves, the trapped-wave phenomenon of edge waves has been attributed to wave refraction near the shore as a result of the variable water depth. The standing edge-wave patterns are presumed to become imprinted on the underwater sediment bed resulting in rip-channel systems. Although it has been argued that rip-channel spacings are correlated to length scales of edge waves (e.g. Bowen and Inman (1971) and R. A. Holman and Bowen (1982)), observed patterns could not be correlated with concurrent or antecedent (one week) hydrodynamic forcing (R. A. Holman et al., 2006; Turner et al., 2007). Also, later (modelling) work could not verify these relationships (e.g. Caballeria et al., 2002; Reniers et al., 2004). Wave groups are another possible forcing mechanism for rip currents (e.g. Reniers et al. (2004)). This will be discussed further in the DUT course Coastal Dynamics II (CIE4309).
2. Downstate implies consecutive beach states under gradually more moderate energy forcing.
3. Rip channels are found in between shore-connected transverse bars or as cross-shore depressions in a shore-parallel bar. The latter bars are also called surf zone crescentic bars systems in literature: surf zone sand bars with alongshore undulations in height and cross-shore position of the bar crest.


