5.2.5: Wave breaking
- Page ID
- 16322
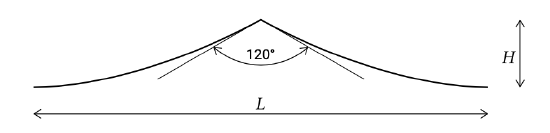
Section 5.2.2 demonstrated how shoaling would increase the wave height until infinity, at least in the absence of a physical limit to the steepness of waves. A wave crest becomes unstable and starts breaking when the particle velocity exceeds the velocity of the wave crest (the wave celerity). This breaking condition corresponds to a crest angle of about 120° (see Fig. 5.9).
Miche breaking criterion and breaker index
Miche (1944) expressed the limiting wave steepness based on Stokes wave theory (a non-linear expansion of the linear Airy theory that better describes steeper waves, see Intermezzo 5.1):
\[\left [\dfrac{H}{L} \right ]_{\max} = 0.142 \tanh (kh)\label{eq5.2.5.1}\]
In deep water Eq. \(\ref{eq5.2.5.1}\) reduces to:
\[\left [\dfrac{H_0}{L_0} \right ]_{\max} = 0.142 \approx \dfrac{1}{7}\]
When the deep-water steepness exceeds this limit, steepness-induced wave-breaking (called white-capping) occurs. Only a limited part of the wave energy is dissipated through white-capping. The steepness \(H_s /L_{o,p}\) of wind waves is often less than 0.05. Note that is the deep water wavelength corresponding to the peak period. Consider for example a deep water wave height \(H_s = 1.5 m\) and a wave period of \(T_p = 5 s\). These can be seen as average conditions for the Dutch coast. We find \(L_{0,p} = 1.56 T_p^2 = 39m\) and \(H_s/L_{0,p} = 1.5/39 = 0.04\). Under these conditions, even for the higher waves in the record, little white-capping is expected.
In shallow water Eq. \(\ref{eq5.2.5.1}\) becomes:
\[\left [\dfrac{H}{L} \right ]_{\max} = 0.142 \dfrac{2\pi h}{L} \approx 0.88 \dfrac{h}{L}\]
This is equivalent to:
\[\gamma = \left [\dfrac{H}{L} \right ]_{\max} = \dfrac{H_b}{h_b} \approx 0.88\label{eq5.2.5.4}\]
with \(\gamma\) is the breaker index, \(H_b\) is the breaking wave height and \(h_b\) is the water depth at the breaking point. Using solitary wave theory – a non-linear wave theory valid for shallow water – gives a slightly different value \(\gamma \approx 0.78\).
The breaker index shows that in the shallow near-shore zone wave-breaking of individual waves starts when the wave height becomes greater than a certain fraction of the water depth. This is called depth-induced breaking since the limiting wave height is governed by a water depth limitation.
The water depth limitation can be explained as follows. The decrease in water depth and the increase in wave heights due to shoaling result in a significant increase in horizontal particle velocities with respect to the wave celerity. When waves approach the shore, the wave celerity is reduced. In addition, we have seen that the wave height increases due to shoaling and the orbital motion within the waves is also changing (see also Sect. 5.4); although the orbit in deep water is a circle, in shallow water the orbit becomes an ellipse with a horizontal axis longer than the vertical axis. The vertical axis of the orbit at the water surface is equal to the wave height. Since shoaling causes an increase in the wave height, the vertical motion of the water particles at the surface must also increase. In addition to this, the horizontal movements grow in relation to the vertical movements, which means that there must be a significant increase of the particle velocity near the surface, until the horizontal particle velocity exceeds the wave celerity.
The Rayleigh distribution demonstrated that the maximum wave height \(H_{\max}\) in a wave record is equal to \(2H_s\). The maximum value of \(H_s/h\) for which the largest waves are breaking is therefore half of the value of the breaker indices. Hence \(H_s/h \approx 0.4-0.5\) based on the Miche criterion.
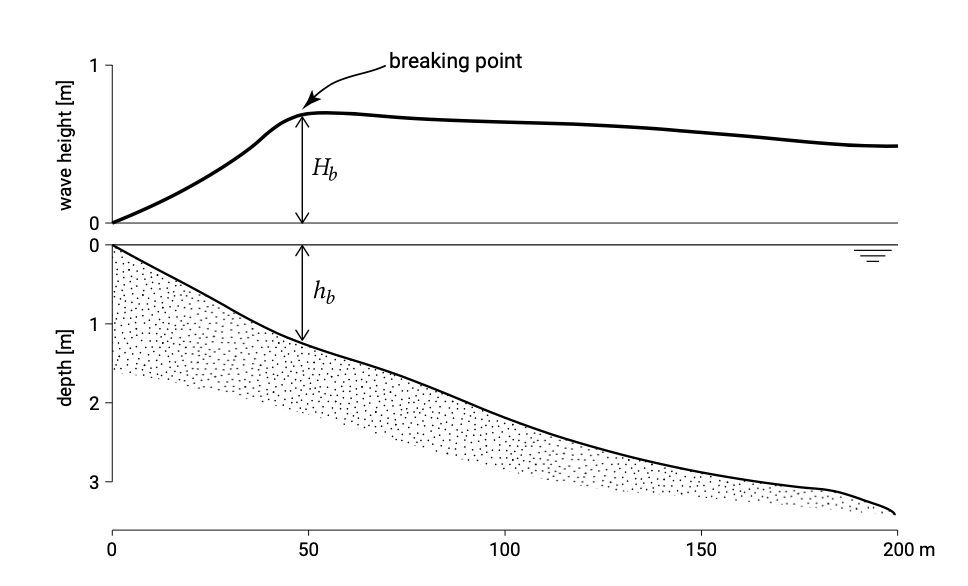
The breaking parameters are shown in Fig. 5.10. The point where the wave height suddenly decreases because the largest wave in the wave field starts breaking is called the breaker point.
The above breaking wave relations have been derived for a horizontal bottom. In reality the bottom will be sloping, which will affect the breaker index. Before we look at the dependency of the breaker index on the angle of the slope, we first consider the process of breaking on a slope.
Effect of bed slope on breaking process
Depending on the wave properties and the angle of the bed slope, the process of breaking takes place in various different ways. Battjes (1974) showed that the Iribarren parameter guides this process. It is defined as follows:
\[\xi = \dfrac{\tan \alpha}{\sqrt{H_0/L_0}}\]
where:
| \(\tan \alpha\) | steepness of the beach | - |
| \(L_0\) | wavelength in deep water | m |
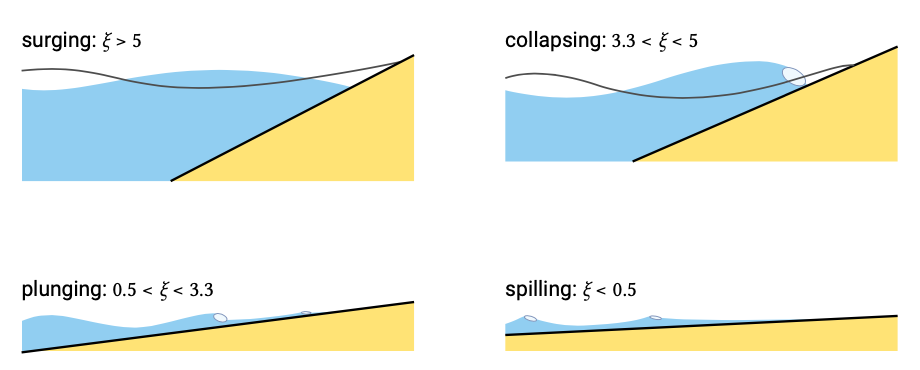
The Iribarren parameter \(\xi\) represents the ratio of the slope steepness \(\tan \alpha\) and the wave steepness. The latter is represented by the deep water steepness instead of the steepness at the breaker point. In irregular waves the Iribarren parameter is often computed with \(H_s\) and \(L_0\) based on \(T_p\). A distinction is made between spilling, plunging and surging breakers depending on the value of \(\xi\) (Fig. 5.11). The transition from surging to plunging breakers is often referred to as collapsing breakers. The typical value of the Iribarren parameter \(\xi\) for the breaker type is also given in the figure. These values are indicative and the transition between the various breaker types is gradual.
Spilling breakers are usually found along flat beaches. These waves begin breaking at a relatively great distance from shore and break gradually (over a distance of 6 to 7 wavelengths) as they approach progressively shallower water. During breaking, a foam line develops at the crest and leaves a thin layer of foam over a considerable distance. There is very little reflection of wave energy back towards the sea. Practically all wave energy is dissipated in the breaking process.
A plunging breaker is a type that is often found on the travel posters for the Pacific Islands. The curling top is characteristic of such a wave. When the curling top breaks over the lower part of the wave, a lot of energy is dissipated into turbulence. Some energy is reflected back to the sea, and some is transmitted towards the coast, while forming a ‘new’ wave.
Surging breakers occur along rather steep shores for relatively long swell waves. The waves surge up and down the slope with minor air entrainment. The breaker zone is very narrow and more than half of the energy is reflected back into deeper water. The breakers form like plunging breakers, but the toe of each wave surges upon the beach before the crest can curl over and fall. It can be questioned whether surging breakers are actually breakers or rather standing waves (caused by interference of the incoming and reflected wave).
A collapsing breaker is between a plunging and a surging breaker and thus in between breaking and non-breaking.
The parameter \(\xi\) indicates that, for a slope, the notions ‘steep’ and ‘gentle’ are relative. A beach slope of 1:100 is usually thought to be gentle, at least for a wind wave with a period of a few seconds. For this beach slope, the earlier considered wave conditions – a deep water wave height \(H_s = 1.5m\) and a wave period of \(T_p = 5s\) - lead to \(\xi = 0.05\). The breakers are thus of the spilling type. For a tidal wave however such a beach slope is rather steep; a tidal wave on a beach does not break and is completely reflected.
How does the bottom slope influence the breaker index \(\gamma\)? Experimental results and theoretical considerations suggest that waves need time to break, so that at steeper slopes they will break at smaller water depths, which results in a larger breaker index. This means that \(\gamma\) increases with increasing \(\xi\) from ca. 0.6 to 0.8 for spilling breakers to 0.8 to 1.2 for plunging breakers. The average value is ca. 0.8 corresponding to the relations found for a horizontal bottom, see e.g. Eq. \(\ref{eq5.2.5.4}\). Battjes and Janssen (1978)
therefore adapted the Miche equation (Eq. \(\ref{eq5.2.5.1}\)) to account for the influence of bottom slope.
Surface roller
Breaking waves generate a layer of air-water mixture, which moves in a landward direction in the upper parts over the water column. This so-called surface roller is thought to act as a temporary storage of energy and momentum. Instead of being dissipated immediately after the breakpoint, organised wave energy is converted into turbulent kinetic energy first (which can be seen from the development of a roller at the face of a breaking wave), before being dissipated ultimately via the production of turbulence. To take this into account, sometimes an additional energy balance equation is used: the roller balance equation. The roller energy \(E_r\) represents the amount of kinetic energy in a roller propagating at the shallow water speed \(c = \sqrt{gh}\).