21.10: Homework Exercises
- Page ID
- 10979
21.10.1. Broaden Knowledge & Comprehension
B1. Search the web for graphs comparing different satellite measurements of the solar irradiance (i.e., the solar constant). Discuss the relative magnitudes of the variation of solar irradiance with time vs. the errors associated with measuring solar irradiance. [Hint: Recall info about accuracy and precision from Appendix A.]
B2. Search the web for maps showing the ice cover on Earth, and how ice cover has changed during the past decades. Discuss these changes in relation to ice-albedo feedback.
B3. Use info from the web to discuss the difference between Bond albedo and geometric albedo. Which one of these albedos is most appropriate to use for studying the radiation budget of other planets?
B4. Search the web for animations or graphs showing/predicting the changes in eccentricity, obliquity, and precession of the Earth over time. Discuss the simplifications made in these diagrams/animations to communicate this info to the general public.
B5. Search the web for more accurate Earth orbital parameters, to improve and expand the data that were in Tables 21-1 and 21-1b. Save and print this table.
B6. Search the web for accurate graphs of ice ages. Discuss what ice-age details are missing or poorly resolved in the ice-age graph in Fig. 21.8.
B7. Search the web for graphs of solar activity or sunspot number, going as far back in time as you can find. Discuss the regular and irregular components of the sunspot cycle.
B8. Search the web for animations or a sequence of still-frames showing how the continents moved to create Pangea, and how they continued to move into their current configuration. Discuss how monsoonal circulations change and alter the continental climates as the continents move.
B9. Search the web for photos of one recent volcanic eruptions that show: (a) ash fallout close to the volcano, and (b) the plume of aerosols injected into the stratosphere, showing their track around the Earth. Discuss the relative amount of global impact due to the one volcanic eruption.
B10. Search the web for photos of beautiful sunsets that were enhanced by volcanic aerosols in the stratosphere. Read ahead in the Atmospheric Optics chapter to see why you can see red skies and blue moons after some volcanic eruptions.
B11. Search the web for info about other major volcanic eruptions that were not listed in Table 21-3. Discuss the impacts of these eruptions on species.
B12. Search the web for the most recent Assessment Report from the Intergovernmental Panel on Climate Change (IPCC), and identify new information and understanding that updates information in this Chapter.
B13. Search the web for additional climate feedback processes that were not listed in Table 21-4, and discuss their relative importance to the ones already listed.
B14. Search the web for data on actual amounts of global warming during the past two decades, and compare to the predictions presented in older IPCC reports. How accurate are climate predictions?
B15. Search the web for animations of Daisyworld evolution. Enjoy.
B16. Lovelock, the inventor of Daisyworld, wrote a more recent book called “The Revenge of Gaia.” If you don’t have time to read the book, search the web for a summary of its key points, and argue either for or against his thesis.
B17. Search the web (particularly IPCC Assessment Reports) that summarize the attributes of the various global climate models (GCMs) that were used for the most recent IPCC climate report. Summarize the commonalities and differences between these various GCMs.
B18. Search the web for color maps showing Köppen climate classification for the whole world. Focus on where you live, and discuss how the climate classification does or does not agree with the climate you observed in your area.
B19. Search the web for color diagrams illustrating the processes involved in these climate oscillations:
a. El Niño or ENSO, including the relationship between trade winds, upwelling water, and SST
b. PDO
c. NAO
d. AO
e. MJO
B20. Often climate variations are indicated on anomaly maps. An example frequently used for ENSO is the sea-surface-temperature anomaly. (a) Define “anomaly map”. (b) Show or give the URL for two other climate anomaly maps on the internet. (c) What is the relationship between sea-surface-temperature anomalies and rainfall shifts or cloud-coverage changes?
B21. Search the web for maps showing the geographic distribution of dominant principal components for any one of the climate oscillations.
B22. Search the web for a Hovmöller diagram for climate oscillations such as MJO in the most recent 6 or 12 months, and analyze it to explain the direction and movement of features.
B23. Based on an internet search, what does the word teleconnection mean with respect to phenomena in the global circulation?
B24. Identify the most-recent major El Niño event, and use the internet to identify or catalog 5 of the worldwide consequences (such as storms or fires).
B25. NCEI is a US-government center. What does the acronym mean, and what can this center do for you? List 8 of the main data types you can access.
B26. Search the web graphs showing observed changes in many of the greenhouse gases.
21.10.2. Apply
A1. Find the radiation input to the Earth system for an albedo of:
| a. 0.1 | b. 0.15 | c. 0.2 | d. 0.25 | e. 0.35 | f. 0.4 |
| g. 0.45 | h. 0.5 | i. 0.55 | j. 0.6 | k. 0.65 | m. 0.7 |
A2. Use the albedoes from exercise A1 to calculate the effective radiation temperature of Earth.
A3. For a global albedo of 0.3, find the radiation input to the Earth system for the following total solar irradiances (W m–2):
| a. 1350 | b. 1352 | c. 1354 | d. 1356 | e. 1358 |
| f. 1360 | g. 1362 | h. 1364 | i 1365 | j. 1367 |
| k. 1368 | m. 1370 | n. 1372 | o. 1374 |
A4. Use the solar irradiance values from exercise A3 to calculate the effective radiation temperatures of Earth. Assume the global albedo is 0.3 .
A5. Find the net radiation out from the Earth system, for an Earth effective radiation emission temperature (°C) of
| a. –19 | b. –17 | c. –15 | d. –13 | e. –11 |
| f. –9 | g. –7 | h. –5 | i. –3 | j. –1 |
| k. 1 | m. 3 | n. 5 | o. 10 | p. 15 |
A6. Given the planets and dwarf planets listed below, find their effective radiation temperatures.
| Planet | Albedo | Planet | Albedo | ||
| a. | Mercury | 0.119 | b. | Venus | 0.90 |
| c. | Mars | 0.25 | d. | Jupiter | 0.343 |
| e. | Saturn | 0.342 | f. | Uranus | 0.30 |
| g. | Neptune | 0.29 | h. | Pluto | 0.40 |
| i. | Eris | 0.96 |
A7. Given an idealized atmosphere having one layer that is totally opaque to infrared radiation, what is the temperature of the planetary surface for:
| (i) exercise A2 | (ii) exercise A4 | (iii) exercise A6 |
A8. Given an Earth with an idealized atmosphere having one layer, but with an infrared window, what is the temperature at Earth’s surface. Use 255 K as the effective emission temperature, and assume the emissivity is:
| a. 0.70 | b. 0.73 | c. 0.76 | d. 0.80 | e. 0.83 | f. 0.86 |
| g. 0.88 | h. 0.91 | i. 0.93 | j. 0.95 | k. 0.97 | m. 0.99 |
A9. Use Fig. 21.6 to answer these questions:
- What fraction of energy absorbed at the Earth’s surface comes from solar radiation?
- What fraction of energy leaving the Earth’s surface consists of (latent + sensible) heat?
- What is the net flux of IR radiation between the Earth’s surface and the atmosphere, and how does this compare to the flux of (latent + sensible) heat?
- What is the total amount of upwelling energy (solar, IR, sensible, latent) that reaches the bottom of the idealized atmosphere in that figure?
- Why is the 79 W m–2 of “solar reflected from atmos.” not included in the energy budget of the atmosphere as one of the outgoing fluxes (Hint: See the Sample Application after that figure)?
- Why is the (sensible + latent) heat flux upward from the top of the atmosphere not shown?
A10(§). On a very large graph, carefully plot two ellipses. One has eccentricity of 0.0 (i.e., is a circle), and the other has an eccentricity of:
| a. 0.05 | b. 0.1 | c. 0.15 | d. 0.2 | e. 0.25 | f. 0.3 |
| g. 0.35 | h. 0.4 | i. 0.6 | j. 0.7 | k. 0.8 | m. 0.9 |
A11(§). Using the data from Table 21-1, find the Earthorbit eccentricity for the following time:
| a. 400 kyr ago | b. 1.1 Myr ago | c. 1.2 Myr ago | d. 1.4 Myr ago | e. 1.6 Myr ago |
| f. 2 Myr ago | g. 625 kyr in the future | h. 1.1 Myr in future | i. 1.3 Myr in future | j. 2 Myr in future |
A12.(§). Same as for A11, but find the obliquity (°).
A13.(§). Same as for A11, but find the climatic precession at the summer solstice (i.e., the e·sin(ϖ) term).
A14(§). Same as for A11 (and A13), but find the ratio of semi-major axis to sun-Earth distance: a/R .
A15(§). Same as A11 (and using your results from A12 - A14), but find the average daily insolation at 65°N during the summer solstice.
A16. Find the sun-Earth distance R (Gm) given an eccentricity of 0.05 and a climatic precession value of:
| a. –0.05 | b. –0.04 | c. –0.03 | d. –0.02 | e. –0.01 |
| f. 0.01 | g. 0.02 | h. 0.03 | i. 0.04 | j. 0.05 |
A17. Use the definition of optical depth from the Beer’s Law section of the Radiation chapter to estimate the optical depth for background “clean” air, which transmits about 94% of incident solar radiation. Also, use data from Fig. 21.17 on recent volcanic eruptions, and compare the “clean” optical depth to the optical depth for:
- Mt. Agung (Indonesia)
- Mt. Fuego (Guatemala
- El Chichon (Mexico)
- Mt. Pinatubo (Philippines)
A18. Find the feedback factor, gain, and system response, given a no-feedback response of ro = 0.2, and a feedback value (F) of:
| a. –8 | b. –6 | c. –4 | d. –2 | e. 1 | f. 2 | g. 3 |
| h. 4 | i. 5 | j. 6 | k. 7 | m. 8 | n. 9 | o. 10 |
A19. Based on the answer to A18, is the feedback negative, stable positive, or run-away positive?
A20. For a no-feedback reference state for Earth, find the no-feedback climate response ro for a blackbody Earth equilibrium radiative temperature of Te* (K):
| a. 200 | b. 210 | c. 220 | d. 230 | e. 240 | f. 250 |
| g. 260 | h. 270 | i. 280 | j. 290 | k. 300 | m. 310 |
A21. Given a reference Earth blackbody radiative temperature of Te* = 255 K and a reference albedo of A* = 0.3 . Find the feedback factor, gain, and total system response if ice-albedo feedback behaves such that the change of Earth albedo (associated with ice coverage changes) with surface temperature (∆A/∆T = –c), where c (K–1) has a value of:
| a. 0.002 | b. 0.005 | c. 0.008 | d. 0.012 | e. 0.015 |
| f. 0.02 | g. 0.03 | h. 0.05 | i. 0.10 | j. 0.2 |
A22. Suppose that doubling of CO2 in the global atmosphere had the same effect as increasing the incoming solar radiation by ∆Ro = 4 W m–2 (due to the increased absorption of solar radiation, as explained in the INFO box on Climate Sensitivity). Given Table 21-4, how much would Earth’s equilibrium temperature change (i.e., find ∆Te in °C) for a reference response with no feedbacks, and for the following feedback process:
| a. water-vapor only | b. lapse-rate only | c. cloud only | d. surface-albedo only | e. all of a - d combined |
A23(§). Program the Daisyworld equations into your spreadsheet. Calculate the surface temperature (K), coverage of white daisies, and coverage of black daisies, for luminosity of:
| a. 0.9 | b. 1.0 | c. 1.1 | d. 1.2 | e. 1.3 |
| f. 1.4 | g. 1.5 | h. 1.6 | i. 1.7 | j. 1.8 |
A24. Describe the climate at
- Oregon coast
- Olympic Mtns (NW corner of Washington)
- central Vancouver Island (British Columbia)
- at the USA-Canada border labels in Fig. 21.25
- north-central California
- north-central Idaho
- western Nevada
- extreme SE California
- central part of Alberta (portion shown in map)
- south central Idaho
21.10.3. Evaluate & Analyze
E1. Derive an equation for the temperature at Earth’s surface vs. the effective radiation temperature, assuming two concentric atmospheric layers that are both opaque to infrared radiation. Hint, consider the methods in the Greenhouse-effect subsection.
E2. Modify the derivations from the Greenhouse-effect subsection to calculate the Earth-surface temperature, given a volcanic-ash-filled single-layer atmosphere that absorbs all IR radiation and absorbs 25% of the solar radiation that tries to move through it. Assume surface albedo is unchanged.
E3. Looking at estimates of past temperatures, the global climate 102 Myr ago was about 2 - 5 °C warmer than present, while 2 Myr ago the global climate was 1.5 - 3.0°C cooler. Is our current “global warming” approaching the normal climate, or is it deviating further away. Discuss.
E4. Explain how the “atmospheric window” in Fig. 21.5 relates to Figs. 8.3 and 8.4 in the Satellites & Radar chapter.
E5. Consider the heat/energy fluxes shown in Fig. 21.6. Assume an atmosphere with a single opaque layer. What if the sun suddenly gets hotter, causing incoming solar radiation to increase by 50%.
Which of the fluxes would change the quickest and which the slowest? How would the new climate equilibrium compare to Earth’s present climate?
E6. In music there is a concept of “beat frequency”. Namely, when two sounds are produced that have nearly the same tone (frequency), you can hear a third tone that depends on the difference between the two frequencies. Look-up the definition of “beat frequency”, and use that info to explain why the Climatic Precession curve in Fig. 21.8 looks the way it does.
E7. a. Given the max and min values of climatic precession plotted in Fig. 21.8, what are the max and min of values of (a/R); namely, the ratio of semi-major axis to sun-Earth distance?
b. Simplify the equation (21.18) for the solar declination angle for the special case of the summer solstice.
c. Given the max and min of obliquities plotted in Fig. 21.8, what are the max and min of solar declination angles (°) for the summer solstice?
d. Combine the info in Figs. 21.11 - 21.13 to estimate the max and min values of solar irradiance (W m–2) during the past 1000 years.
e. Given your answers to (a) - (d) above, which has the largest effect on the value of daily-average insolation at 65°N during the summer equinox: climatic precession, obliquity, eccentricity, or solar irradiance?
E8. In Fig. 21.8, the Daily Average Insolation graph is based on a combination of the previous three graphs in that figure. Looking at the nature of the signals in all four top graphs in Fig. 21.8, which of the top 3 graphs best explains the Insolation, and which of the top 3 least explain the Insolation? Why?
E9(§). Table 21-1 shows only the first N = 4 or 5 terms for Earth’s orbital factors. Use all the terms in Table 21-1b, on the next page to calculate and accurately reproduce the first 3 graphs in Fig. 21.8.
| Table 21-1b. Factors in orbital series approximations. | |||
| index | A | P (years) | ϕ (degrees) |
| Eccentricity: | |||
|
i= 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
0.010739 0.008147 0.006222 0.005287 0.004492 0.002967 0.002818 0.002050 0.001971 0.001797 0.002074 0.001525 0.001491 0.001316 0.001309 0.001300 0.001306 0.001261 0.001344 0.001058 |
405,091. 94,932. 123,945. 98,857. 130,781. 2,373,298. 977,600. 105,150. 486,248. 688,038. 100,805. 76,909. 134,300. 103,158. 118,077. 109,936. 127,123. 55,002. 96,727. 346,318. |
170.739 109.891 –60.044 –86.140 100.224 -168.784 57.718 49.546 148.744 137.155 24.487 102.380 –167.676 69.234 –51.163 –146.081 –139.827 30.098 27.612 178.662 |
| Obliquity: | |||
|
j= 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
0.582412° 0.242559° 0.163685° 0.164787° 0.095382° 0.094379° 0.087136° 0.064348° 0.072451° 0.080146° 0.072919° 0.033666° 0.033722° 0.030677° 0.039351° 0.030375° 0.024733° 0.025201° 0.021615° 0.021565° 0.021270° 0.021851° 0.014725° |
40,978. 39,616. 53,722. 40,285. 41,697. 41,152. 9,572,151. 29,842. 28,886. 40,810. 41,319. 39,465. 39,784. 40,455. 29,768. 29,926. 29,690. 40,622. 41,880. 54,030. 53,426. 40,108. 28,997. |
86.645 120.859 –35.947 104.689 -112.872 60.778 39.928 -15.13 -155.175 -70.983 10.533 –31.614 77.554 71.757 145.835 160.109 144.926 –173.656 –144.933 –79.670 –178.441 –24.566 124.744 |
| Climatic Precession: | |||
|
k= 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
0.018986 0.016354 0.013055 0.008849 0.004248 0.002742 0.002386 0.001796 0.001908 0.001496 0.001325 0.001266 0.001165 0.001304 0.001071 0.000970 0.001002 0.000936 0.000781 0.000687 0.000575 0.000577 0.000651 0.000416 0.000497 0.000392 |
23,682. 22,374. 18,953. 19,105. 23,123. 19,177. 19,025. 22,570. 19,260. 16,465. 18,804. 23,178. 18,873. 22,425. 22,528. 22,323. 23,064. 19,334. 19,417. 18,656. 24,199. 19,146. 22,639. 22,938. 22,600. 23,233. |
44.374 –144.166 154.212 –42.250 90.742 61.600 74.660 –145.502 119.333 141.244 169.748 -110.52 -78.477 -161.509 16.058 47.804 126.199 38.272 -77.364 14.412 134.011 -99.821 130.819 188.622 109.059 46.89 |
| Simplified from Laskar, Robutel, Joutel, Gastineau, Correia & Levrard, 2004: A long-term numerical solution for the insolation quantities of the Earth. “Astronomy & Astrophysics”, 428, 261-285. | |||
E10. Use the orbital data for Earth to answer the following. How many years in the future is the first time when the perihelion will coincide with the summer solstice? This is important because it means that summers will be hotter and winters colder in the N. Hemisphere, because the N. Hemisphere will be tilted toward the sun at the same date that the Earth is closest to the sun.
E11 Show that the right-hand approximation in eq. (21.18) for the solar declination is the same as eq. (2.5). [Hints: Consider that in summer, Earth is 90° further along its orbit than it was in Spring. Use trig identities that relate sines to cosines. Consider the definitions of various orbital angles, as summarized in the INFO box on Sun-Earth Distance.]
E12. Explain why Pangea’s climate would be different than our present climate. [Hint: Consider global circulations and monsoonal circulations, as discussed in the General Circulation chapter.]
E13. a. Use the definitions of optical depth and visual range from the Beer’s Law section of the Solar & IR Radiation chapter to find a relationship for visibility (km) as a function of optical depth \(\ \tau\)
b. Use your answer from (a) with the data from Table 21-3 to estimate the atmospheric visibilities associated with the following volcanic eruptions:
| (i) Lake Toba | (ii) Mt. Tambora | (iii) Krakatau |
E14. For every type of climate feedback, explain why runaway climate change is not possible. [Or if it is possible, show how runaway climate changes applies for only a limited change of Earth temperatures before a new stable climate equilibrium is reached. Can you recall any Hollywood movies that showed runaway climate change, with or without reaching a stable equilibrium?]
E15. For the feedback interconnections shown in Fig. 21.18, the feedback outcomes are only: negative (damped), positive (amplified), or runaway (increasing without limit). Can you think of a different type of interconnection or process that could cause the system response to oscillate? Explain.
E16. Ice-albedo processes were used for an idealized illustration of feedback. Try to develop your own feedback concepts that account for the following (and ignores all other feedbacks except the fundamental radiative feedback). Suppose there is a CO2 feedback process whereby warmer Earth temperatures cause the oceans to release more CO2 into the air. But more CO2 in the air acts to partially close the IR window sketched in Fig. 21.5.
a. What info or what relationships do you need to be able to figure out the feedback? [Only list the info needed — do not actually find these relationships.] b. If you are good at calculus and if assigned by your instructor, then try to create a governing equation similar to that used for ice-albedo feedback, then take the derivatives as was done in the Higher Math Feedback Example box. There is no single correct answer — many different approximations and solutions might be reasonable. Justify your methods.
E17. For feedbacks in the Earth climate system, use error-propagation methods as discussed in Appendix A, to propagate the errors listed in the feedback (F) column of Table 21-4 into the other columns for feedback factor (f), gain (G), & system response (r).
E18. Do outside readings to explain how the following abrupt climate-change processes work (Table 21- 4). Also, explain if feedback is positive or negative.
- meridional overturning ocean circulation
- fast Antarctic & Greenland ice-sheet collapse
- volcanoes
- biogeochemical
- methane release due to hydrate instability and permafrost)
E19.(§) For a daisyworld
- Redo the calculation shown in this chapter.
- What happens to the temperature over black and white daisies if transport Tr changes to 0 or 1?
- What happens if you start with initial conditions of 100% coverage by white or black daisies?
- What happens if you take a time step increment of 2, 4, or 8?
- What parameter values prevent homeostasis from occurring (i.e., eliminate the nearly constant temperature conditions on a fecund daisyworld?
- Is it possible for homeostasis to occur on Earth, given the large fraction of area covered by oceans?
E20(§). In Fig. 21.24 for Daisyworld, homeostasis is possible for luminosities spanning only a certain range. What changes to the daisy growth parameters or equations would permit homeostasis for luminosities spanning a greater range? Confirm your results by solving the resulting Daisyworld equations with your new parameters.
E21. Where in the world (but NOT in any region plotted in Fig. 21.25) would you expect to find the climate in Table 21-8 above. (Hint, consider info in the General Circulation chapter, and also use the Köppen climate definitions in Table 21-6.)
E22(§-difficult). Find the covariance matrix, the eigenvectors and eigenvalues (using some other resource such as a web-based eigenvector calculator), leading 2 principal components (PCs), interpret the results, and reconstruct (synthesize) the original data as approximated using the dominant 2 PCs, given time series in Table 21-9. Assume that the locations for these time series correspond to the geographic locations shown in Fig. 21.a of the PCA INFO box.
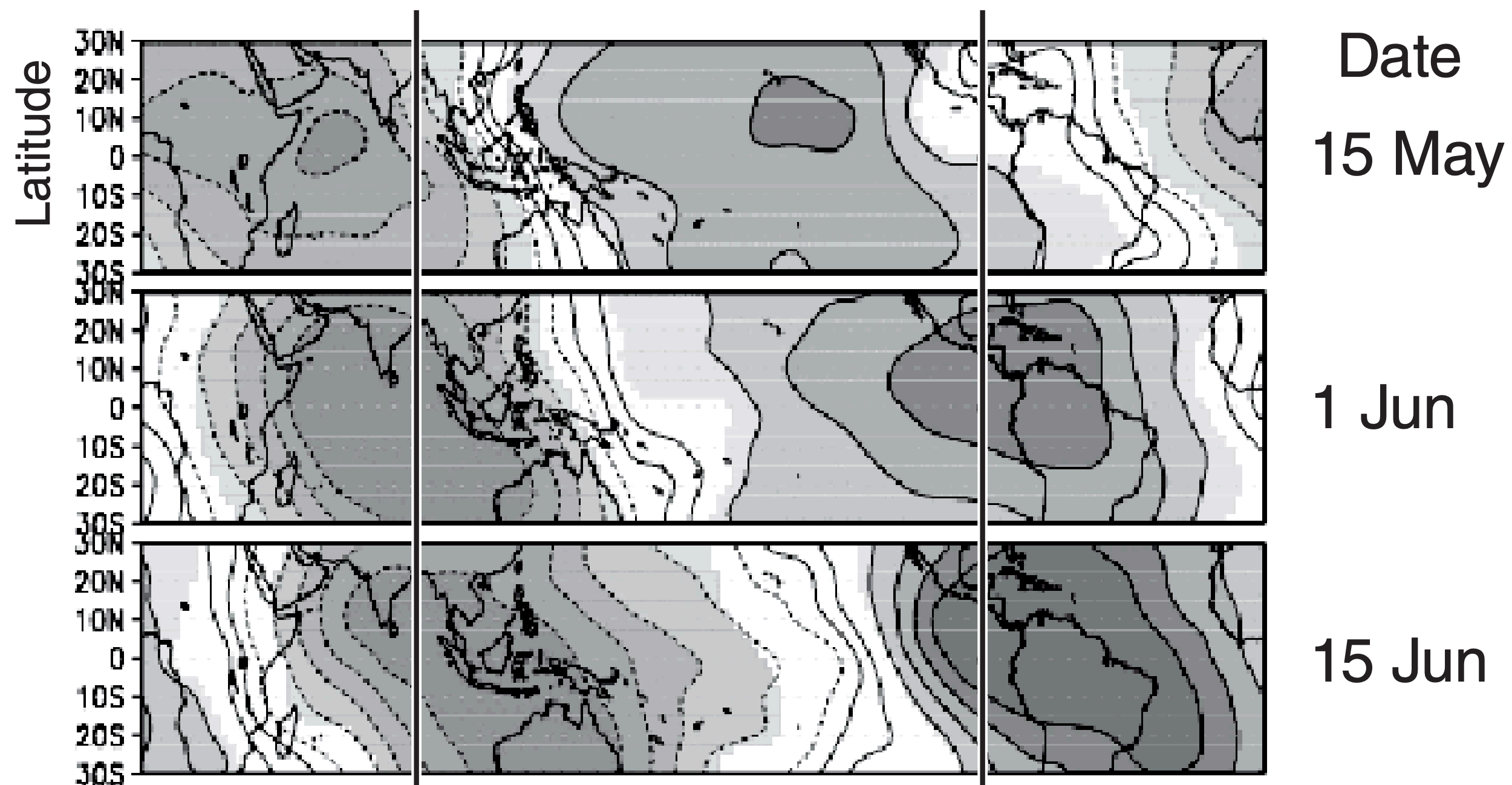
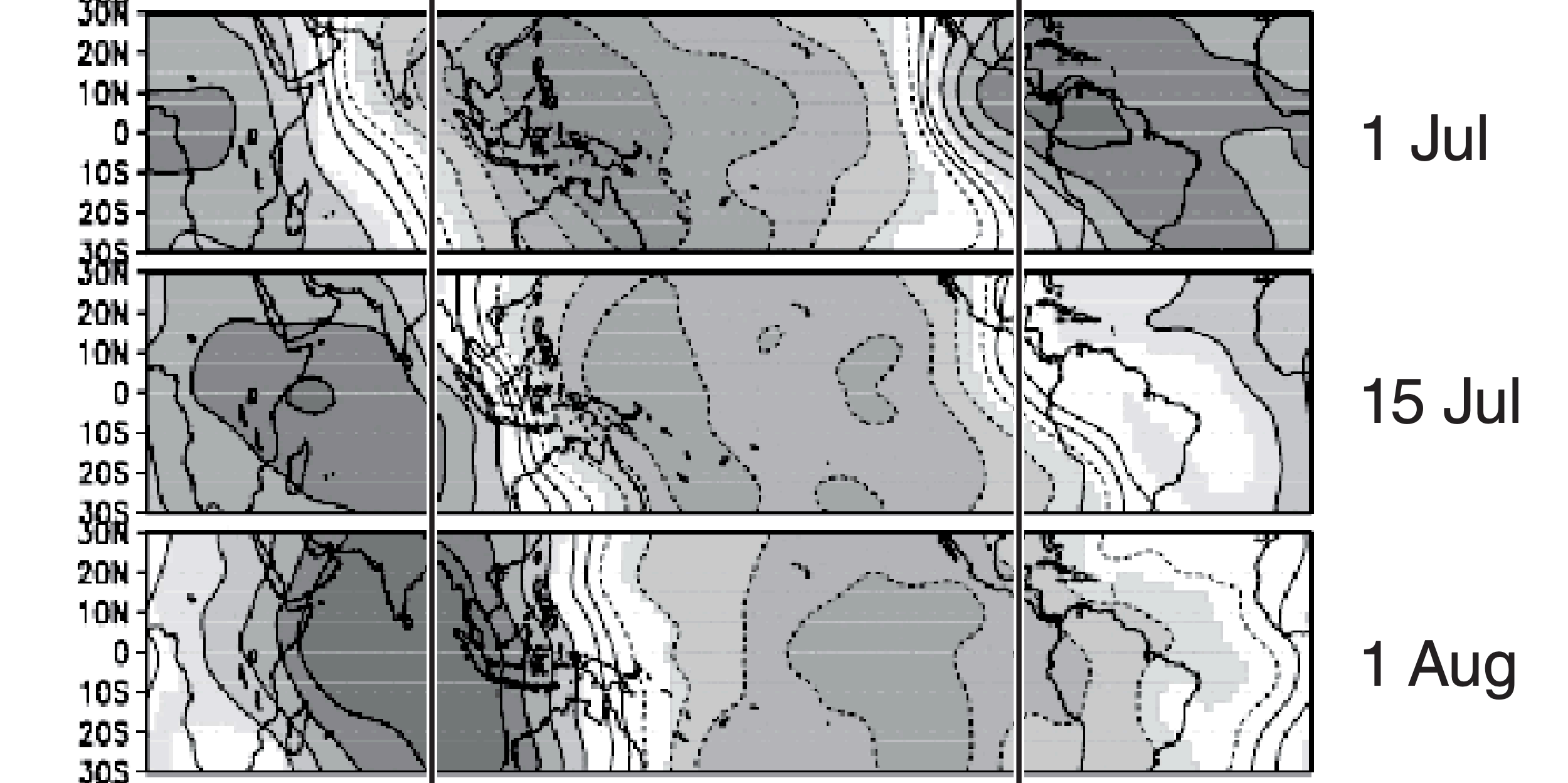
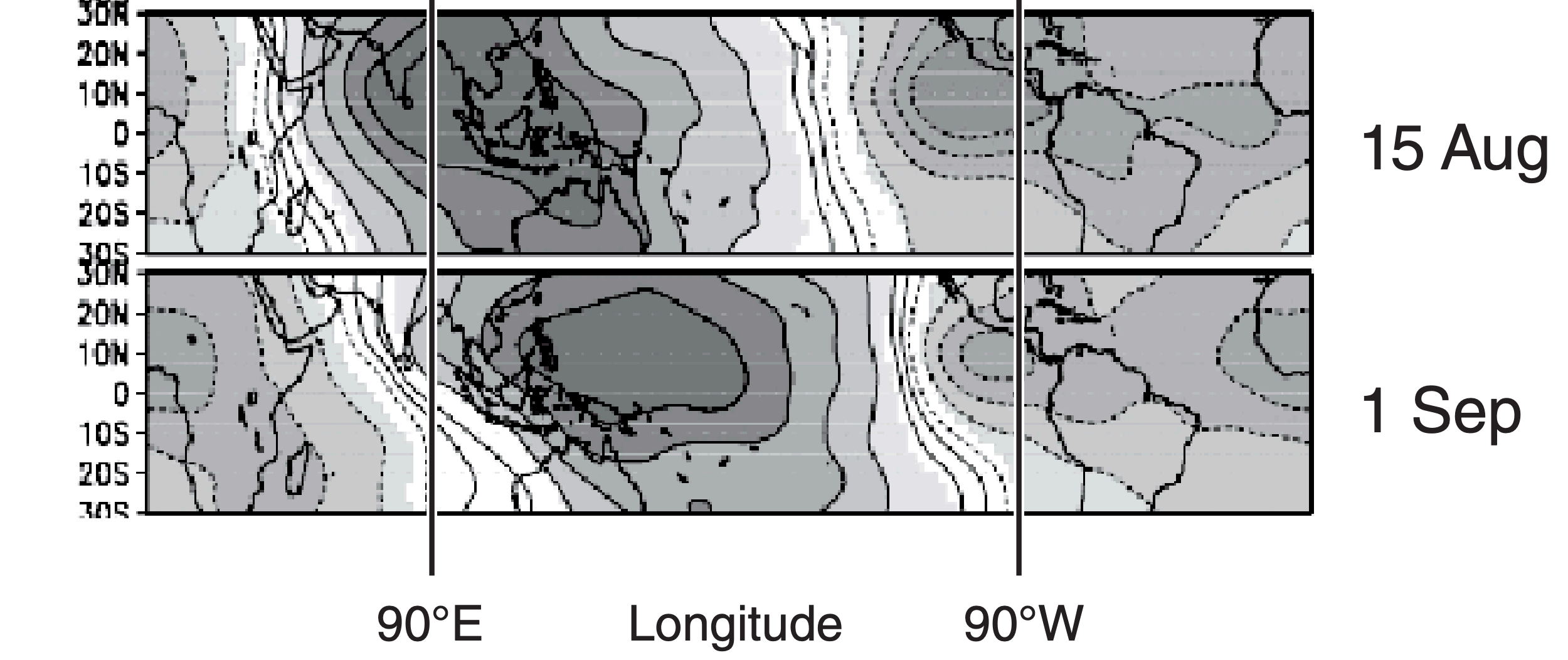
E23. Given the Hovmöller diagram in Fig. 21.29, determine the zonal speed and direction (toward east or west) that features move.
| Table 21-8. Names of Köppen climate classes. | ||
| Exercise | Code | Name |
|
a b c |
Af Am Aw |
equatorial climate monsoon climate tropical savanna climate |
|
d e f g |
BWh BWk BSh BSk |
warm desert climate cold desert climate warm semi-arid climate (warm steppe clim.) cold semi-arid climate (cold steppe climate) |
|
h i j k l m n o |
Csa Csb Cwa Cwb Cwc Cfa Cfb Cfc |
warm mediterranean climate temperate mediterranean climate warm humid subtropical climate temperate humid subtropical climate cool humid subtropical climate warm oceanic/marine; or humid subtropical temperate oceanic/marine climate cool oceanic/marine climate |
|
p q r s t u v w x y z aa |
Dsa Dsb Dsc Dsd Dwa Dwb Dwc Dwd Dfa Dfb Dfc Dfd |
warm continental (mediterranean continental) temperate continental (mediter. continental) cool continental climate cold continental climate warm humid continental climate temperate humid continental climate cool continental clim.; cool subarctic climate cold continental clim.; cold subarctic climate warm humid continental climate temperate humid continental climate cool continental clim.; cool subarctic climate cold continental clim.; cold subarctic climate |
|
ab ac |
ET EF |
tundra climate ice cap climate |
| Table 21-9. Time series for PCA exercise. | ||||
| Location Index: | j = 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Location: | NW | NE | SW | SE |
| Year | Air Temperature (°C) | |||
| i = 1 | 9 | 1 | 1 | 8 |
| 2 | 7 | 2 | 1 | 8 |
| 3 | 5 | 3 | 2 | 7 |
| 4 | 7 | 4 | 5 | 6 |
| 5 | 9 | 5 | 9 | 5 |
| 6 | 7 | 6 | 9 | 5 |
| 7 | 5 | 5 | 5 | 5 |
| 8 | 7 | 4 | 5 | 6 |
| 9 | 9 | 3 | 4 | 7 |
| 10 | 7 | 2 | 1 | 8 |
21.10.4. Synthesize
S1. What if emitted IR radiation were constant — not a function of temperature. How would Earth’s climate be different, if at all?
S2. Create an energy balance to determine Ts and Te for an atmosphere with:
- 2 opaque atmospheric layers (no window)
- 3 opaque atmospheric layers (no window)
- extrapolate your theory so it works with more layers
S3. Suppose the same side of the Earth always faced the sun, and the atmosphere was stationary over the Earth. Assume no heat transport between Earth’s cold and warm sides. Write the equations (along with your justification) for energy balances for each side of the Earth, for the following scenarios:
- a single-layer opaque atmosphere.
- a single-layer atmosphere, but having an IR window.
S4. Suppose radioactive decay deep inside the Earth caused as much heat transport into the bottom of the atmosphere as is incoming solar radiation into the top of Earth’s atmosphere. Work out the energy budgets, and calculate steady-state Earth-surface temperatures. Discuss feedbacks. (Hint, assume a single-layer opaque atmosphere.)
S5. Estimate the variation in insolation if Earth’s orbit were to have eccentricity of 0.8.
S6. Given idealized ozone holes centered over each pole, where each hole extends 25° of latitude from the pole. In each hole, assume that the atmosphere is totally transparent to IR radiation. Assume that Earth’s climate can be divided in to latitude bands of uniform surface temperature: hot near the equator, temperate at mid latitudes, and cold directly under the ozone holes. (a) Devise energy-balance equations for each latitude band, (b) find the average surface temperature within each band, and (c) find the overall Earth-surface average temperature. Justify any assumptions you make.
S7. Suppose a long-lasting solar storm ionizes the air and totally closes the infrared window on Earth’s sunny side. However, Earth’s shady side is not affected, allowing an atmospheric window to exist in the infrared. (a) What is the steady-state Earth-surface temperature (averaged over the whole globe)? (b) Show your budget equations justify your assumptions to support your answer.
S8. For Daisyworld, start with global coverages of 50% dark and 50% light daisies. Assume that no bare ground is allowed at any time, although relative coverage of light and dark daisies can change. (a) Devise equations to describe this scenario, and (b) compare your results with the Daisyworld equations and results earlier in this chapter. (c) Does the new Daisyworld allow homeostasis? (d) Is the new Daisyworld more or less sensitive to changes in luminosity?
S9. If runaway climate change caused the Earth to reach a new warmer equilibrium, would the Earth’s climate be able to recover to the climate we currently have? What positive and/or negative feedback processes would encourage such recovery?
S10. Would global warming alter:
- the global circulation?
- thunderstorm severity?
- thunderstorm frequency?
- hurricane (or typhoon) severity?
- hurricane (or typhoon) frequency?
- hurricane (or typhoon) tracks?
Explain how.
S11. Discuss the scientific accuracy of recent Hollywood movies where the theme was weather or climate disasters.
S12. Repeat the principal component analysis from the INFO box, but when you calculate the table of principal components (PC), use the temperature anomaly T’ in eq. (21.50) instead of T. Then finish all the remaining calculations using these new PCs.
What is the sum of elements in each PC (i.e., the sum of each column in the PC table)? What is the relationship between your plotted PCs and Fig. 21.c? When you synthesize the signal using only PC1, how does your result compare to Fig. 21.d?
Outcome: you are synthesizing T’ and not T. Most researchers use PCA to focus on the anomaly.


