21.4: Feedbacks
- Page ID
- 10192
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)21.4.1. Concept
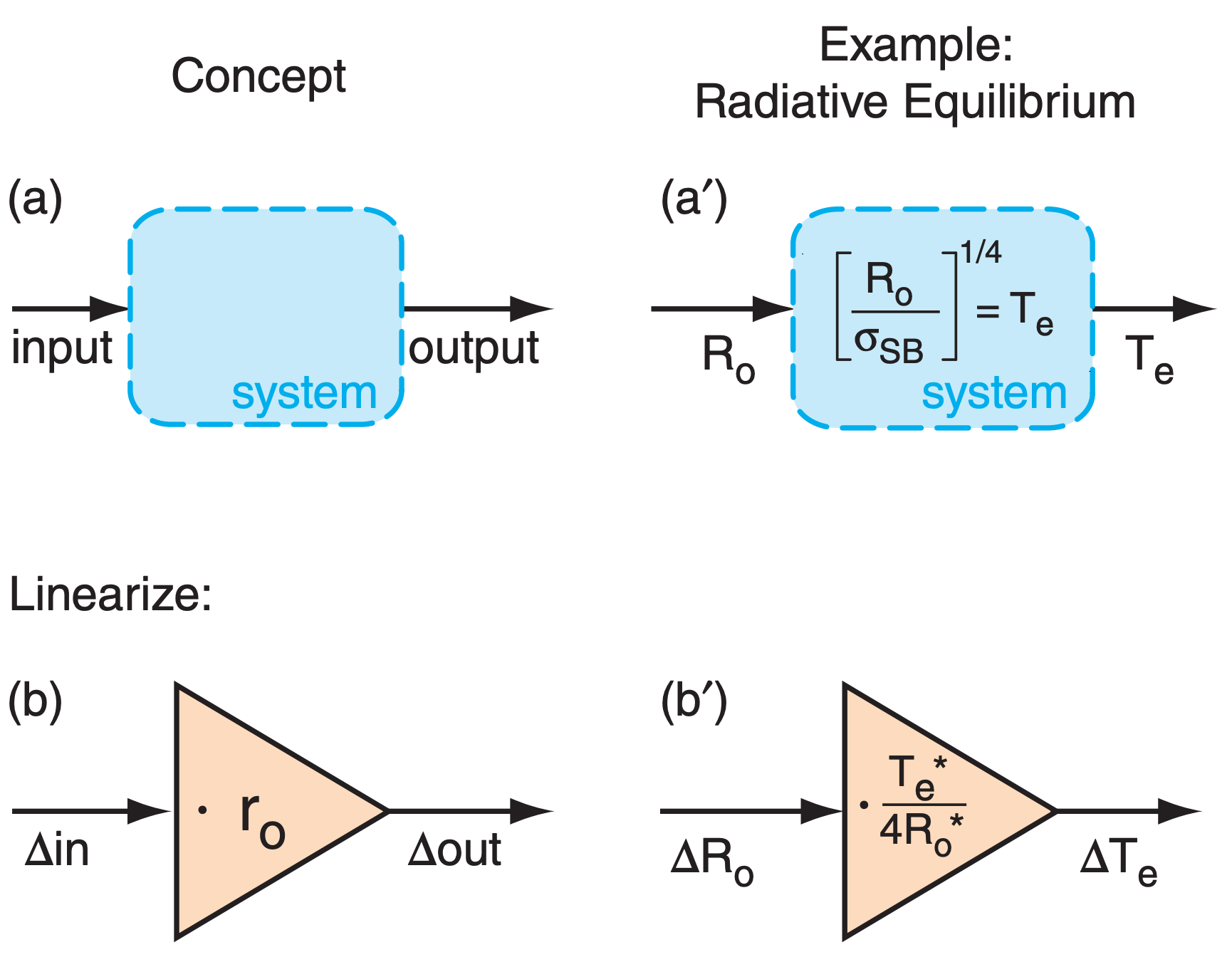
Consider a system or physical process with an input and output (Fig. 21.18a). This system might be linear (described by a straight line when output is plotted vs. input) or nonlinear (described by a curved line). Various values of input give various values of output.
Choose one particular set of input and output values as a reference state of the system. Find the slope ro of the line at this reference point. This slope describes the response of the output (∆out) to a small change of input (∆in). Namely,
\begin{align}\Delta \text { out }=r_{o} \cdot \Delta \text { in }\tag{21.21}\end{align}
as sketched in Fig. 21.18b. The slope is a straight line. Thus, even if the original system is nonlinear, this slope describes a linearized approximation to the system response at the reference point.
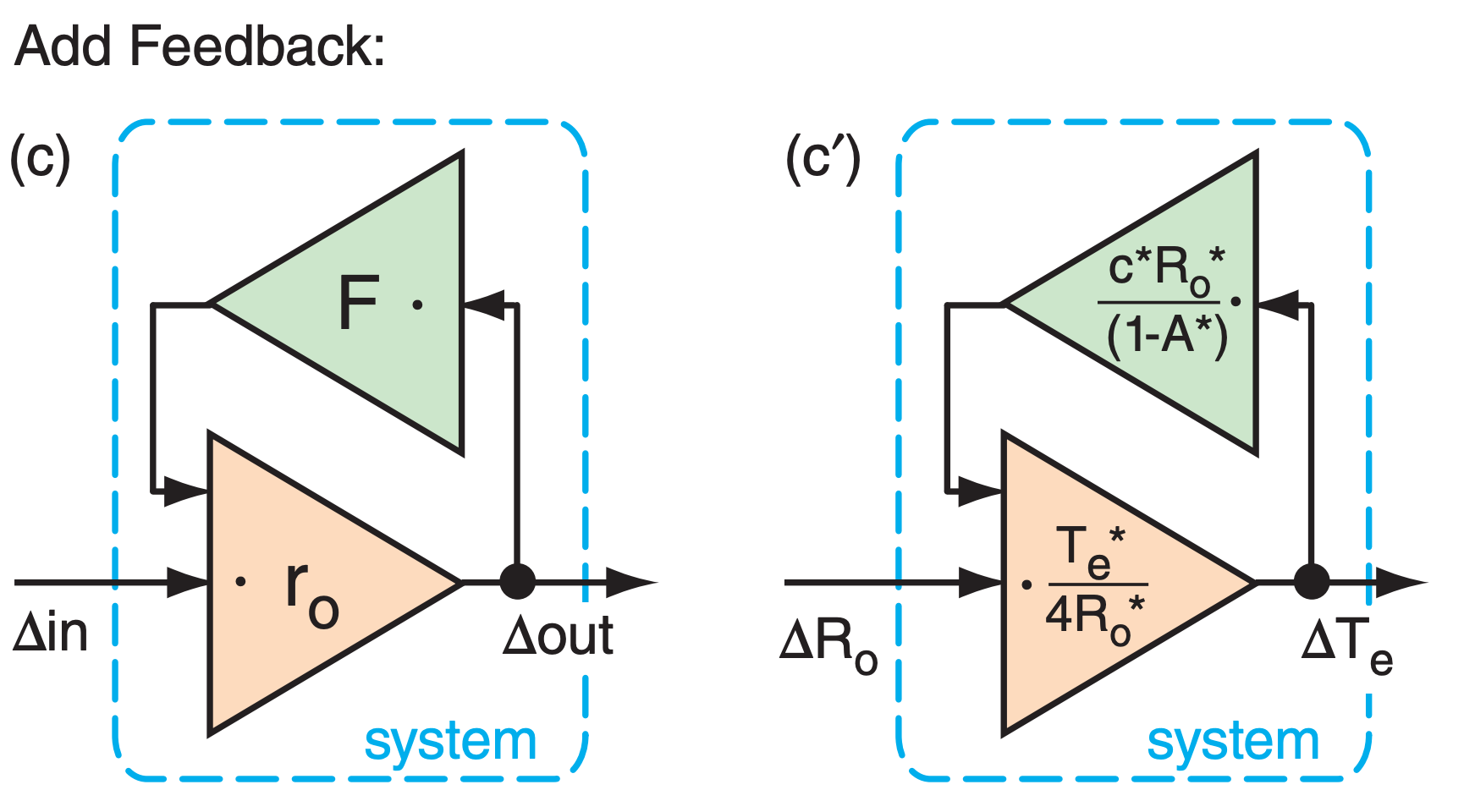
Feedback (Fig. 21.18c) is where the output signal is added to the input via some feedback process F:
\begin{align}\Delta \text { out }=r_{o} \cdot[\Delta \mathrm{in}+F \cdot \Delta \mathrm{out}]\tag{21.22}\end{align}
A linear approximation is also used for this feedback. The feedback is internal to the system (Fig. 21.18c). Thus the amount of feedback responds to changes in the system. Contrast that to inputs, which are considered external forcings that do not respond to changes within the system.
The previous feedback equation can be rewritten as
\begin{align}\Delta \text { out }=r_{o} \cdot \Delta \mathrm{in}+f \cdot \Delta \mathrm{out}\tag{21.23}\end{align}
where the feedback factor f is given by
\begin{align}f=r_{o} \cdot F\tag{21.24}\end{align}
Solving eq. (21.33) for ∆out gives:
\begin{align}\Delta \text { out }=\frac{1}{(1-f)} \cdot r_{o} \cdot \Delta \text { in }\tag{21.25}\end{align}
Eq. (21.25) looks similar to eq. (21.21) except for the new factor 1/(1–f). In electrical engineering, this factor is called the gain, G:
\begin{align}G=\frac{1}{(1-f)}\tag{21.26}\end{align}
Some climate researchers use a different definition of gain than electrical engineers. See the INFO Box on the next page
If we rewrite eq. (21.25) as
\begin{align}\Delta \text { out }=r \cdot \Delta \text { in }\tag{21.27}\end{align}
then we see that the linearized process WITH feedback (eq. 21.27) looks identical to that without (eq. 21.21) but with a different response:
\begin{align}r=\mathbf{G} \cdot r_{o}\tag{21.28}\end{align}
If f ≥ 1, then the feedback is so strong that the response increases without limit (i.e., a runaway response), and no equilibrium exists. If 0 < f < 1, then there is positive feedback with gain G > 1 that leads to an amplified but stable new equilibrium. If f < 0, then there is negative feedback with gain G < 1 that damps the response toward a different stable equilibrium.
For N feedback processes that are independent of each other and additive, the total gain is
\begin{align}G=\left[1-\sum_{i=1}^{N} f_{i}\right]^{-1}\tag{21.29}\end{align}
where fi is the feedback factor for any one process i.
Sample Application
Suppose ro = 0.1 and F = –3. Find the feedback factor, gain, and compare system responses with and without feedback.
Find the Answer
Given: F = –3, no-feedback system response ro = 0.1
Find: f = ? , G = ? , r = ? = response with feedback
Use eq. (21.24):
f = (0.1) · ( –3) = –0.3 is the feedback factor
Use eq. (21.26):
G = 1 / [1 – (–0.3)] = 0.77 is the gain
Use eq. (21.28):
r = (0.77)·(0.1) = 0.077 is the system response with feedback, compared to ro = 0.1 without.
Check: Units all dimensionless. Magnitudes OK.
Exposition: This system is damped. It has negative feedback. This feedback diminishes the response. For many systems, the output units differ from the input units, in which case ro , F, and r would have units.
Some climate researchers define the gain g as
\(\ g=\frac{\Delta o u t-\Delta o u t_{o}}{\Delta o u t}\)
where ∆outo is the background response with NO feedbacks. Thus:
\(\ g=\frac{G \cdot r_{o} \cdot \Delta i n-r_{o} \cdot \Delta i n}{G \cdot r_{o} \cdot \Delta i n}=1-\frac{1}{G}\)
But G = 1/(1–f) from eq. (21.26). Thus
\(\ g=f\)
Namely, the “gain” used in some climate studies is the feedback factor used in this chapter and in electrical engineering.
21.4.2. Idealized Example
To illustrate feedback, use the simple no-atmosphere blackbody radiative-equilibrium system of Fig. 21.1. The net solar input per square meter of the Earth’s surface is
\begin{align}R_{o}=(1-A) \cdot S_{o} / 4\tag{21.30}\end{align}
(see the INFO box on the 3rd page of this chapter). The IR-radiation output is described by the Stefan-Boltzmann law, resulting in the following energy balance of input = output:
\begin{align}R_{o}=\sigma_{S B} \cdot T_{e}^{4}\tag{21.31}\end{align}
as indicated in Fig. 21.18a’.
The dashed lines in Fig. 21.2 show how an input of Ro = 240.2 W m–2 (So = 1361 W m–2) results in an output Te ≈ 255.1 K. Use this blackbody Earth-equilibrium condition as the reference state, and denote the reference values with asterisks (Ro*, Te*). The thick cyan curved line in Fig. 21.2 shows how Te varies nonlinearly for different inputs of Ro, assuming A = 0.294 is constant (i.e., no feedback other than the background outgoing IR).
21.4.2.1. No Feedback
Focus on this no-feedback example first (Fig. 21.18b’). For small solar-input variations ∆Ro about its reference state, the corresponding temperature change ∆Te can be approximated by a straight line tangent to the curve at the reference point (Fig. 21.2), as defined by
\begin{align}r_{o}=\Delta T_{e} / \Delta R_{o}\tag{21.32}\end{align}
Based on eq. (21.31), the slope ro of this straight line (see Higher Math box on the previous page) is:
\begin{align}r_{o}=\frac{1}{4 \cdot \sigma_{S B} \cdot T_{e} *^{3}}=\frac{T_{e}^{*}}{4 \cdot R_{o}^{*}}=0.266 \mathrm{K} /\left(\mathrm{W} \cdot \mathrm{m}^{-2}\right)\tag{21.33}\end{align}
Start with no feedback, as described by the energy balance of eq. (21.31).
\(\ R_{o}=\sigma_{S B} \cdot T_{e}^{4}\)
Take the derivative:
\(\ d R_{o}=4 \sigma_{S B} \cdot T_{e}^{3} d T_{e}\)
Rearrange to find the change of output with input (dTe/dRo ),
\(\ \frac{\partial T_{e}}{\partial R_{o}}=\frac{1}{4 \cdot \sigma_{S B} \cdot T_{e}^{3}}\)
Finally, convert to finite differences:
\begin{align}r_{o}=\frac{\Delta T_{e}}{\Delta R_{o}}=\frac{1}{4 \cdot \sigma_{S B} \cdot T_{e}^{3}}\tag{21.33}\end{align}
Another form of this answer can be found by multiplying the numerator and denominator by Te, and then substituting eq. (21.31) in the denominator:
\(\ r_{o}=\frac{T_{e}}{4 \cdot R_{o}}\)
Sample Application
For ice-albedo radiative-equilibrium with a blackbody-Earth reference state, find the feedback factor and gain. Compare system responses with and without feedback.
Find the Answer
Given: Te*= 255 K, Ro*=240 W·m–2, A*=0.294, c*= 0.01 K–1
Find: ro = ? (K/W·m–2), f = ? , G = ? , r = ? (K/W·m–2)
Use eq. (21.33) for the no-feedback system response:
ro = (255K)/(4 · 240W·m–2) = 0.266 K/(W·m–2)
Use eq. (21.36) for the feedback factor:
f = (0.01 K–1)·(255K) / [4 · (1 – 0.294)] = 0.90 (dim’less)
Use eq. (21.26): G = 1/(1 – 0.90) = 10.4 (dimensionless)
Use eq. (21.28):
r = (10.4) · [0.266 K/(W·m–2)] = 2.75 K/(W·m–2)
Check: Response is reasonable. Units OK.
Exposition: This illustrates positive feedback where the response is amplified. For example, ∆So ≈ 1 W·m–2 due to sunspot cycle (Fig. 21.11) implies ∆Ro = 0.175 W·m–2, giving ∆Te = r· ∆Ro = 0.48°C variation in equilibrium radiation temperature due to sunspots with feedback, compared with ∆Te=0.266°C without.
21.4.2.2. Ice Albedo Feedback
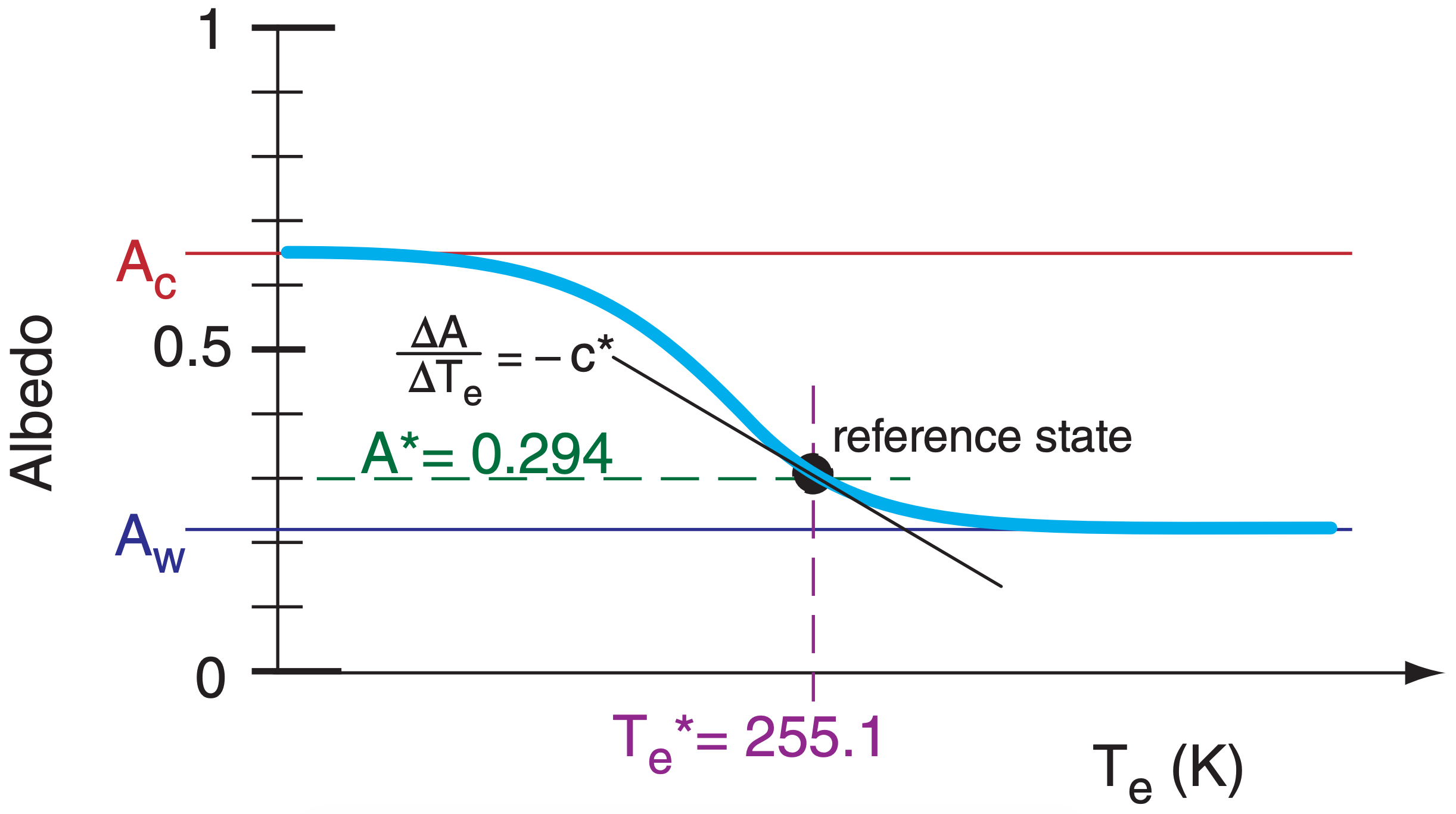
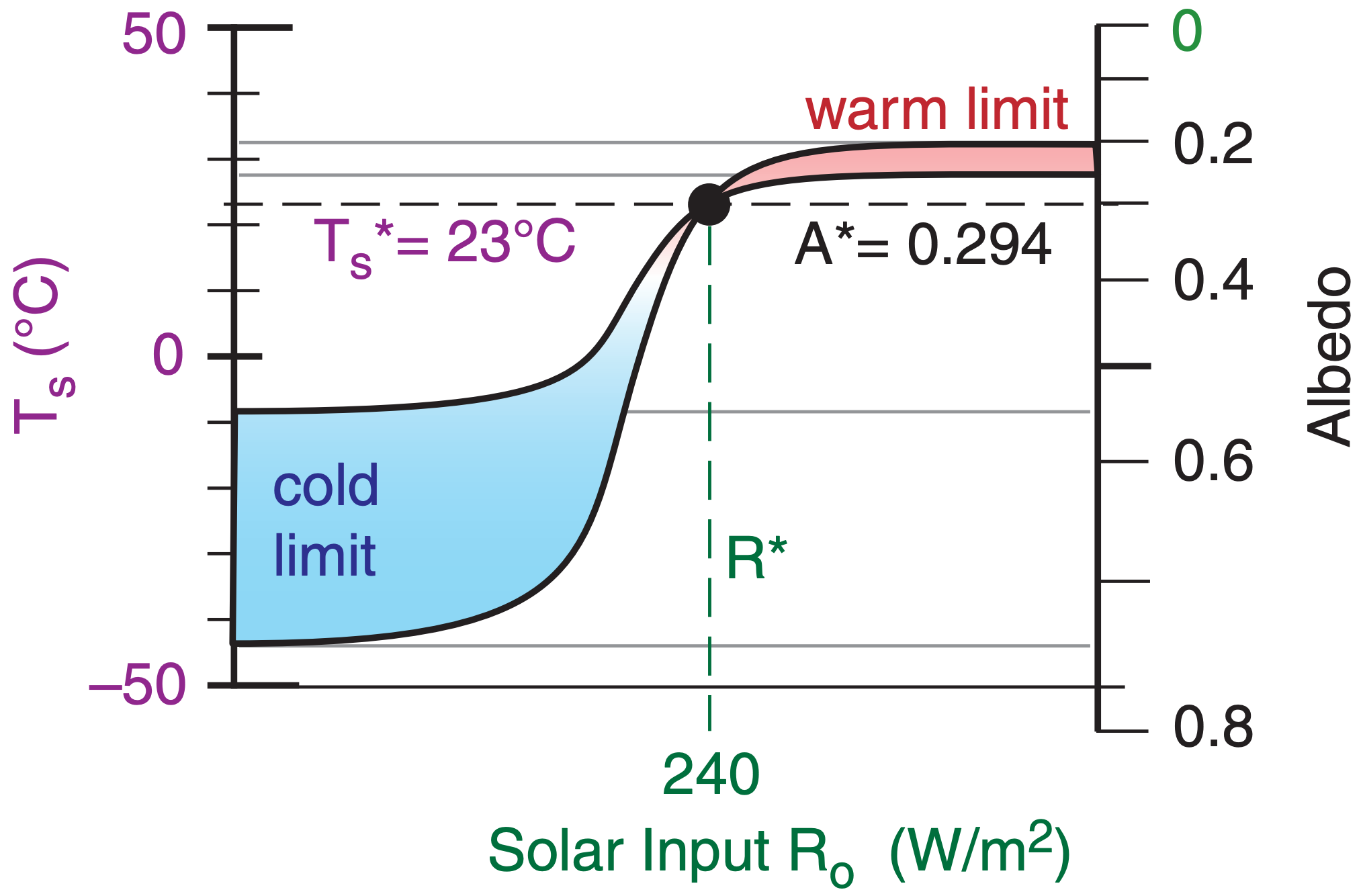
Next, add ice-albedo feedback by allowing the albedo to vary with temperature. Changes in temperature Te alter the areal extent of highly reflective ice caps and glaciers, thereby changing the albedo (A) between two extremes (Fig. 21.19). A warm limit Aw assumes 0% snow cover, and is based on the reflectivities of the ground, crops, cities, and oceans. A cold-limit Ac represents 100% snow cover, causing a highly reflective Earth. The blackbody Earth state is useful as a reference point (Te* = 255 K, A* = 0.294).
Use the slope (thin line in Fig. 21.19) of the A vs. Te curve at the reference point as a linear approximation of the nonlinear feedback (thick line). Numerical simulations of the global climate suggest this slope is:
\begin{align}\frac{\Delta A}{\Delta T}=-c^{*}\tag{21.34}\end{align}
where c* = 0.01 K–1. The ice-albedo feedback described here is highly oversimplified, for illustrative purposes.
For this idealized ice-albedo radiative-equilibrium case, the feedback equation (21.23) becomes:
\begin{align}\Delta T_{e}=r_{o} \cdot \Delta R_{o}+f \cdot \Delta T_{e}\tag{21.35}\end{align}
where ro was given in eq. (21.33), and where
\begin{align}f=\frac{c^{*} \cdot T_{e}^{*}}{4 \cdot\left(1-A^{*}\right)}\tag{21.36}\end{align}
(see the Higher Math box on the next page).
The resulting gain is
\begin{align}G=\frac{4 \cdot\left(1-A^{*}\right)}{4 \cdot\left(1-A^{*}\right)-c^{*} \cdot T_{e}^{*}}\tag{21.37}\end{align}
After multiplying ro by the gain to give r, we find that the temperature response to solar-input variations (when feedbacks ARE included) is:
\begin{align}r=\frac{\left(1-A^{*}\right) \cdot T_{e}^{*}}{R_{o}^{*} \cdot\left[4 \cdot\left(1-A^{*}\right)-c^{*} \cdot T_{e}^{*}\right]}\tag{21.38}\end{align}
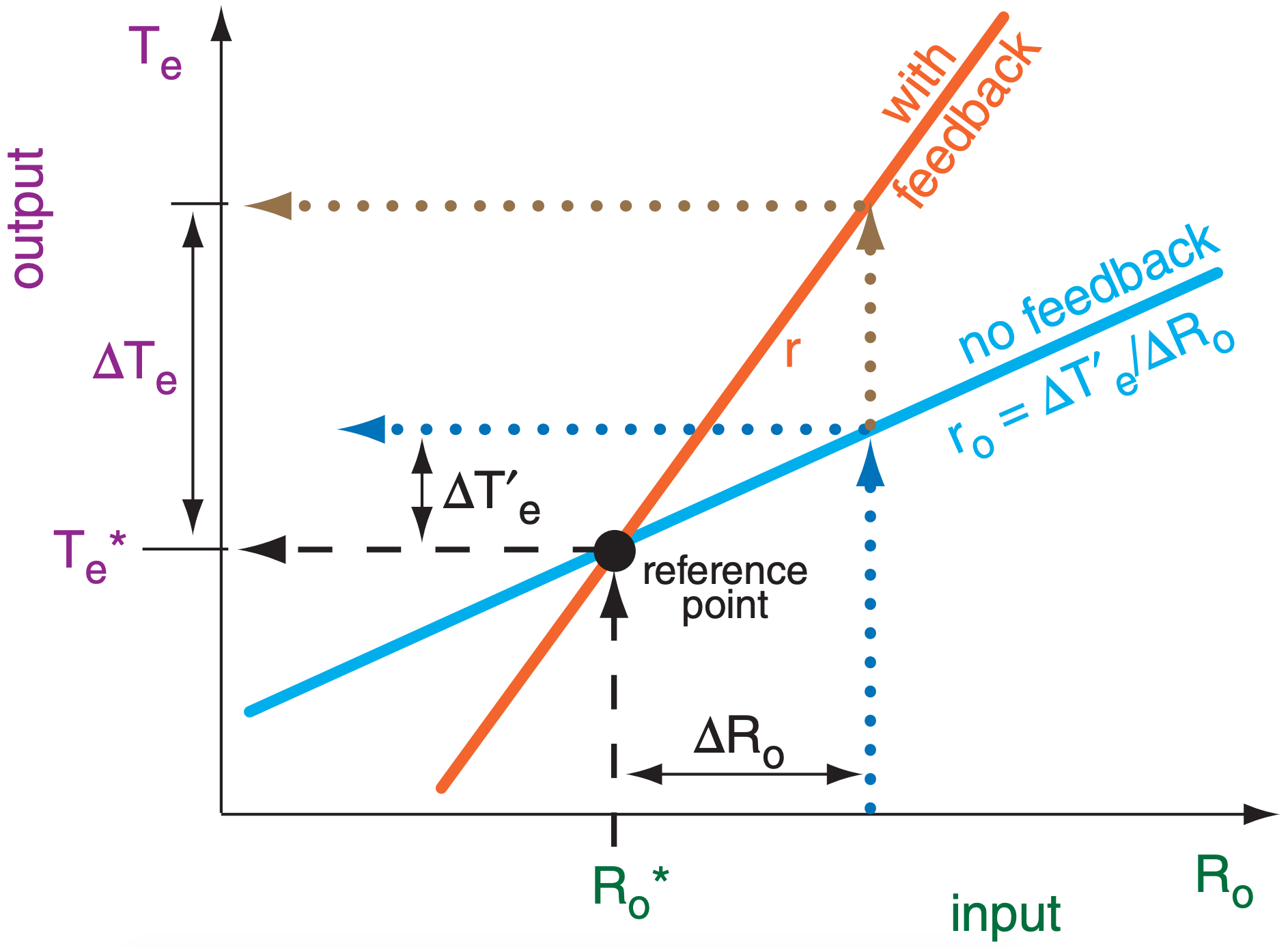
Fig. 21.20 shows how the total response r with feed back differs from the ro without. With feedback, eq. (21.32) becomes:
\begin{align}\Delta T_{e}=r \cdot \Delta R_{o}\tag{21.39}\end{align}
Table 21-4 lists some feedbacks that can affect Earth’s climate. These are briefly discussed next.
|
Table 21-4. Feedbacks affecting Earth’s climate. (+) = positive, (–) = negative feedbacks F = Feedback parameter (W·m–2)·K–1 f = feedback factor (dimensionless) G = Gain (dimensionless) r = system response K/(W·m–2). This is also known as the sensitivity, λ. |
||||
| Processes for gradual climate change: | ||||
| Feedback | F | f = ro·F | G = 1/ (1–f) | r = G·ro |
|
IR Radiative (–)
|
ro = 0.27 0.31 |
|||
| Water-vapor (+) | 1.6 ±0.3 | 0.50 | 1.98 | 0.61 |
| Lapse-rate (–) | –0.6 ±0.4 | –0.19 | 0.84 | 0.26 |
| Cloud (+) | 0.3 ± 0.7 | 0.09 | 1.1 | 0.34 |
| Surface albedo (+) | 0.3 ±0.1 | 0.09 | 1.1 | 0.34 |
| Ocean CO2 (+) | ||||
| Biological (–) | ||||
| Processes for Abrupt climate change: | ||||
Biogeochemical |
||||
From IPCC, AR5, 2013, Chapter 9, Table 9.5 & Fig. 9.43.
For ice-albedo feedback, infinitesimal variations in solar irradiance dSo and albedo dA cause infinitesimal changes in equilibrium temperature dTe:
\begin{align}d T_{e}=\frac{\partial T_{e}}{\partial S_{o}} d S_{o}+\frac{\partial T_{e}}{\partial A} d A\tag{21.a}\end{align}
To find the factors that go into this equation, start with a simple radiative-equilibrium balance:
\begin{align}T_{e}=\left[\frac{(1-A) \cdot S_{o}}{4 \cdot \sigma_{S B}}\right]^{1 / 4}\tag{21.3}\end{align}
and take the derivative ∂Te /∂So :
\(\ \frac{\partial T_{e}}{\partial S_{o}}=\frac{1}{4}\left[\frac{(1-A) \cdot S_{o}}{4 \cdot \sigma_{S B}}\right]^{-3 / 4} \cdot\left[\frac{1-A}{4 \cdot \sigma_{S B}}\right]\)
Substituting eq. (21.3) into this gives:
\(\ \frac{\partial T_{e}}{\partial S_{o}}=\frac{1}{4}\left[T_{e}\right]^{-3} \cdot\left[\frac{1-A}{4 \cdot \sigma_{S B}}\right]\)
which we can rewrite as:
\(\ \frac{\partial T_{e}}{\partial S_{o}}=\frac{1}{4} \cdot T_{e} \cdot\left[\frac{1-A}{4 \cdot \sigma_{S B} \cdot T_{e}^{4}}\right]\)
Solve (21.3) for So and substituting into the eq. above:
\(\ \frac{\partial T_{e}}{\partial S_{o}}=\frac{1}{4} \cdot T_{e} \cdot\left[\frac{1}{S_{o}}\right]\)
You can similarly find ∂Te /∂A from eq. (21.3) to be:
\(\ \frac{\partial T_{e}}{\partial A}=\frac{-T_{e}}{4 \cdot(1-A)}\)
When these derivatives are plugged into eq. (21.a) and applied at the reference point (So*, Te*, A*), the result is:
\(\ d T_{e}=\frac{T_{e}^{*}}{4 \cdot S_{o}^{*}} d S_{o}-\frac{T_{e}^{*}}{4 \cdot\left(1-A^{*}\right)} d A\)
Albedo decreases when Earth’s temperature increases, due to melting snow and retreating glacier coverage:
\(\ d A=-c^{*} \cdot d T_{e}\)
where c* is the magnitude of this variation at the reference point. Plugging this into the previous eq. gives:
\begin{align}d T_{e}=\frac{T_{e}^{*}}{4 \cdot S_{o}^{*}} d S_{o}+\frac{c^{*} \cdot T_{e}^{*}}{4 \cdot\left(1-A^{*}\right)} d T_{e}\tag{21.b}\end{align}
Next, take the derivative of eq. (21.30):
\(\ d R_{o}=[(1-A) / 4] \cdot d S_{o}\)
Dividing this by eq. (21.30) shows that:
\(\ \frac{d R_{o}}{R_{o}}=\frac{d S_{o}}{S_{o}}\)
Plug this into eq. (21.b), and convert from calculus to finite differences:
\(\ \Delta T_{e}=\frac{T_{e}^{*}}{4 \cdot R_{o}^{*}} \cdot \Delta R_{o}+\frac{c^{*} \cdot T_{e}^{*}}{4 \cdot\left(1-A^{*}\right)} \cdot \Delta T_{e}\)
Compare this with eq. (21.23) to realize that:
\(\ r_{o}=\frac{T_{e}^{*}}{4 \cdot R_{o}^{*}} \quad(\text { eq. } 21.33) \quad \text { and } \quad f=\frac{c^{*} \cdot T_{e}^{*}}{4 \cdot\left(1-A^{*}\right)}\)
Thus,
\(\ F=\frac{f}{r_{o}}=\frac{c^{*} \cdot R_{o}^{*}}{\left(1-A^{*}\right)} \quad \text { and } \quad G=\frac{4 \cdot\left(1-A^{*}\right)}{4 \cdot\left(1-A^{*}\right)-c^{*} \cdot T_{e}^{*}}\)
For the idealized (toy model) example in this section, the reference values are:
Te* = 255.1 K = radiative equilibrium temperature
So* = 1361 W·m–2 = solar irradiance
Ro* = 240.2 W·m–2 = solar input / m2 Earth’s surface
A* = 0.294 (dimensionless) = albedo
c* = 0.01 K–1 =albedo response to temperature change
21.4.3. Infrared Radiative (IR) Feedback
IR is the strongest feedback — it dominates all others. It was already discussed as the “radiation out” term in eq. (21.2). This important negative (–) feedback allows the Earth to have an equilibrium state. Even a small change in Earth’s temperature results in a strong compensating energy loss because IR radiation is proportional to the 4th power of Te in the Stefan-Boltzmann equation. This strong damping keeps Earth’s climate relatively steady.
As we have seen, the reference black-body response to changes in net solar input is ro = 0.267 K/ (W·m–2). Global climate models that include more realistic atmospheric absorption and emission of IR radiation find ro = 0.31 ± 0.01 K/(W·m–2).
21.4.4. Water-vapor Feedback
Warmer air can hold more water vapor, which absorbs and re-radiates more IR radiation back to the surface and reduces the atmospheric window sketched in Fig. 21.5. The warmer surface warms the air, resulting in a very strong positive feedback (see Table 21-4). The upper troposphere is where this feedback is most effective.
Water vapor is an important natural greenhouse gas. If the climate warms and the upper tropospheric water-vapor content increases to the point where the atmospheric window is mostly closed (net atmospheric emissivity e ≈ 1), then we return to the negative feedback sketched in Fig. 21.4 and steady Earth temperature of Ts = 30°C from eq. (21.6).
Sample Application
Given the feedbacks listed in Table 21-4, what is the total response.
Find the Answer
Given: Table 21-4. Use realistic Earth for ro.
Find: r = ? K/(W·m–2).
Assume: total response is based on only those feedback processes for which numbers are given in the table.
Use eq. (21.29): G = 1 / [1 – Σ f]
G = 1 / [ 1 – (0.50 – 0.19 + 0.09 + 0.09)]
G = 1 / [1 – 0.49] = 1.96
Use eq. (21.28): r = G · ro
r = 1.96 · 0.31 = 0.61 K/(W·m–2).
Check: Units OK. Physics OK.
Exposition: For each ∆R = 1 W·m–2 change in solar input, the Earth-system response with all feedbacks is ∆T = 0.61 K, which is twice the response (0.31 K) without feedback (other than the background IR feedback). {CAUTION: The total response is NOT equal to the sum of the individual responses r. Instead, use the sum of feedback factors f to get the net feedback.]
21.4.5. Lapse-rate Feedback
The simple model of Fig. 21.4 uses the same air temperature TA to determine IR radiation both up to space and down toward the Earth. However, in the real atmosphere the temperature decreases with an average lapse rate 6.5 °C·km–1 in the troposphere. Thus, colder temperatures at the top of the troposphere emit less upward IR radiation to space than is emitted downward from the warmer bottom of the troposphere. This difference in upward and downward IR radiation is part of our normal climate, causing our normal temperatures.
Global warming tends to reduce the lapse rate. Namely, the temperature difference diminishes between the top and bottom of the troposphere. Relative to each other, IR radiation out to space will increase and IR radiation down toward the Earth will decrease. The net effect is to cool the Earth system. Thus, lapse-rate feedback is negative (Table 21-4).
Water-vapor and lapse-rate feedbacks are closely related, and are often considered together. Their combined effect is a modest positive feedback.
Sample Application
Use Table 21-4 to estimate the combined water-vapor and lapse-rate response, rwv.lr .
Given Table 21-4: fwater.vapor = 0.50, flapse.rate = –0.19
Find: rwv.lr = ? K/(W·m–2)
Assume: ro = 0.31K/(W·m–2) for a realistic Earth.
For multiple feedbacks, we must use eq. (21.29):
G = 1 / [1 – (0.50 – 0.19)] = 1.45
Use eq. (21.28):
rwv.lr = 1.45 · [0.31 K/(W·m–2)] = 0.45 K/(W·m–2)
Check: Units OK. Magnitude OK.
Exposition: This r corresponds to G = 1.45, f = 0.311, & F = 1.003, which agrees with IPCC AR5 Fig. 9.43.
21.4.6. Cloud Feedback
Cloud feedback is likely important, but the details are poorly understood. Relative to clear skies, clouds at all heights cause cooling by reflecting incoming solar radiation. But clouds also cause warming by trapping (absorbing and re-radiating back towards the surface) upwelling IR radiation. The small difference between these large opposing forcings can have very large error, depending on cloud type and altitude. For our present climate, the net effect of clouds is cooling.
Table 21-4 indicates a positive feedback for clouds, based on global climate modeling. Namely, an increase in radiative input to the Earth system would decrease the cloud cover, thus causing less cooling. But much more research must be done to gain more confidence in cloud-feedback processes.
Sometimes aerosol feedback is grouped with cloud feedback. Aerosols (microscopic solid or liquid particles in the air) can have similar effects as cloud droplets. However, some aerosols such as sulfates are darker than pure water droplets, and can absorb more solar radiation to cause atmospheric warming. As already discussed, volcanoes can inject sulfate aerosols into the stratosphere. Phytoplankton (microscopic plant life) in the ocean can release into the atmospheric boundary layer a chemical called dimethyl sulfide, which can later be oxidized into sulfate aerosols.
A greenhouse gas (GHG) is an atmospheric gas that absorbs and emits IR radiation. Of particular concern are gases that absorb and emit within the 8 to 14 µm wavelength range of the atmospheric window. As the concentrations of such gases increase, the atmospheric window can close due to the increased atmospheric emissivity (Fig. 21.5), resulting in global warming.
Greenhouse gases, ranked by importance, are:
(1) water vapor (H2O),
(2) carbon dioxide (CO2),
(3) methane (CH4),
(4) nitrous oxide (N2O),
(5) ozone (O3),
(6) halocarbons [e.g., freon CFC-12 (C Cl2 F2)]
Except for (6), most greenhouse gases have both natural and anthropogenic (man-made) sources. CO2 is of particular concern because it is released by humans burning fossil fuels (coal, oil) for energy.
21.4.7. Ice–albedo (Surface) Feedback
This positive feedback was discussed earlier in the idealized feedback example, where we found a response of r = 2.75 K/(W·m–2) in the Sample Application. More realistic estimates from Global Climate Model simulations are r = 0.27 to 2.97 K/ (W·m–2). At our current reference temperature, this feedback mostly affects the climate at high latitudes.
This positive-feedback sensitivity applies only over the limited range of Fig. 21.19 for which albedo can vary with temperature. At the cold extreme of a completely snow-covered Earth (snowball Earth), the albedo is constant at its cold-limit value Ac. At the warm extreme the Earth has no ice caps or snow cover, and albedo is constant at Aw.
At these two extremes, the negative feedback of IR radiation again dominates, leading to steady Earth temperatures. For snowball Earth, cold-limit albedo estimates are in the range of 0.55 ≤ Ac ≤ 0.75. When used in the radiation balance of eq. (21.3) the cold-limit blackbody temperature is 197 K ≤ Te ≤ 228 K, yielding a surface temperature (Ts = 1.161·Te, from eq 21.10) of –44°C ≤ Ts ≤ –8°C.
For the warm limit (assuming that clouds having 37% albedo still cover roughly 70% of the Earth) 0.20 ≤ Aw ≤ 0.25, and the equilibrium blackbody temperature is 259 K ≤ Te ≤ 263 K. This corresponds to a surface temperature of 28°C ≤ Ts ≤ 33°C using eq. (21.10). Thus, runaway global warming or cooling is not possible beyond these bounds (see Fig. 21.21).
The Intergovernmental Panel on Climate Change (IPCC) states that climate sensitivity is “a measure of the climate system response to sustained radiative forcing. It is defined as the equilibrium global average surface warming” (∆Ts) “following a doubling of CO2 concentration.”
Based on research by international teams using global climate models, IPCC suggests in their 5th Assessment Report (AR5, 2013) that “this sensitivity is likely to be in the range of” ∆Ts = “1.5 to 4.5°C with a best estimate of 3.2°C” for a doubling of the greenhouse gas CO2. This temperature rise would be equivalent to a radiative forcing (∆Ro in Fig. 21.18b’ & c’; abbreviated as RF by IPCC) of 3.4 ±0.8 W·m–2.
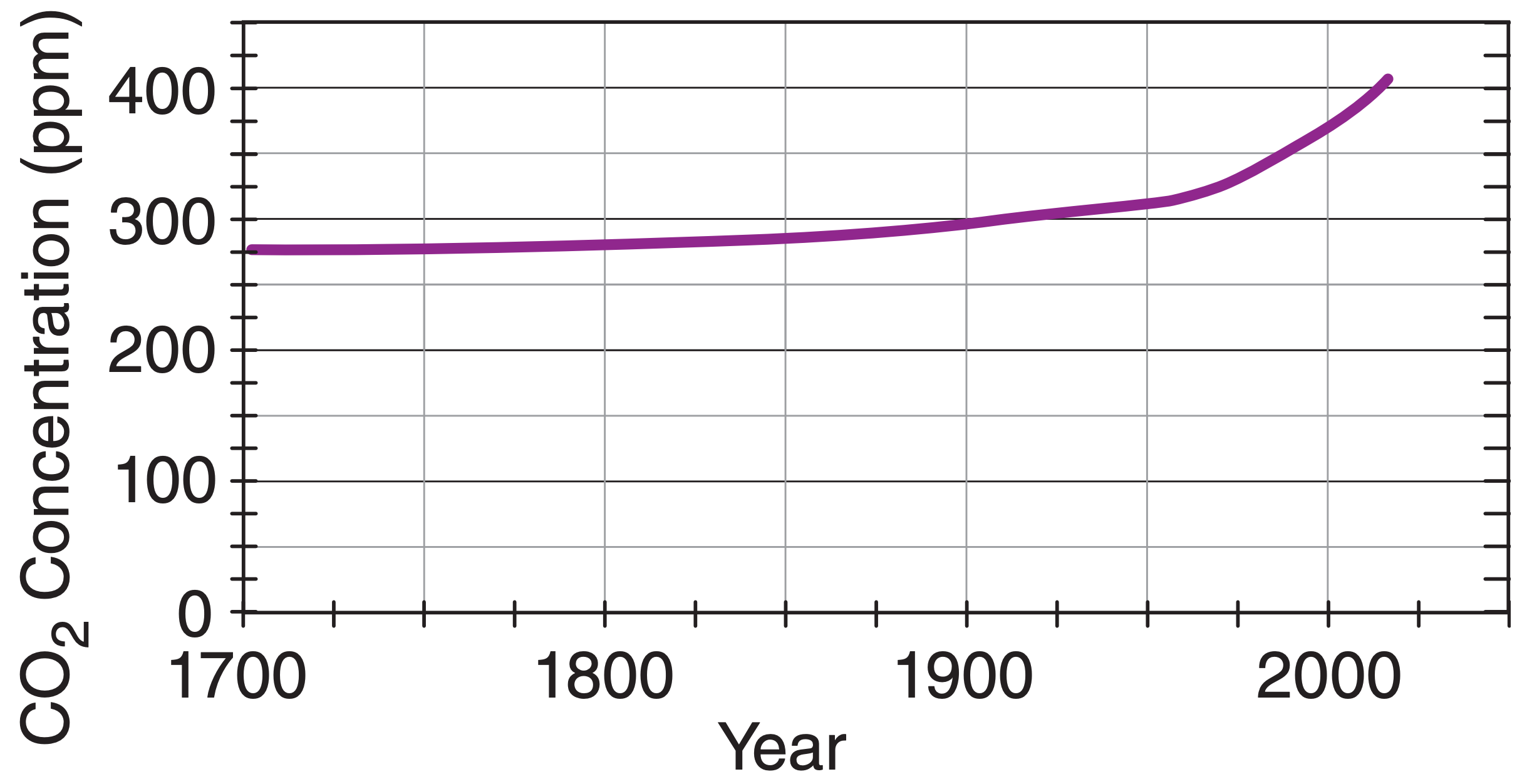
CO2 has not doubled yet, but since year 1700 the concentration increased from 275 to 410 ppm (Fig. 21.k).
IPCC is particularly concerned about anthropogenic forcings, because these can be mitigated by people. Since year 1750 — the start of the industrial age — people have inadvertently altered the Earth-system net radiative forcing as follows (IPCC AR5 Table 8.6):
| Anthropogenic Process | ∆Ro or RF (W·m–2) |
| Well-mixed greenhouse gases (CO2 + CH4 + N2O + Halocarbons) | +2.83 |
| O3 in stratosphere | –0.05 |
| O3 in troposphere | 0.40 |
| H2O from CH4 in stratosphere | 0.07 |
| Surface albedo/land use | –0.15 |
| Surface albedo/carbon on snow | 0.04 |
| Aerosols/ direct | -0.35 |
| Jet contrails | +0.01 |
Total Anthropogenic (was not estimated in the AR5 report) in AR4 was estimated as +1.6 range [0.6 to 2.4]
Compare this to a natural process:
| Solar irradiance change | +0.05 |
The large anthropogenic effects relative to the natural solar variations is what motivates policy makers to take action.
21.4.8. Ocean CO2 Feedback
Warmer seawater can hold less dissolved carbon dioxide (CO2) than colder water (see INFO box on next page). Hence global warming will cause oceans to release CO2 into the atmosphere. Greater atmospheric CO2 concentrations reduce the atmospheric window due to an increase in net atmospheric emissivity e, and thus cause the atmosphere to re-radiate more IR radiation back toward the Earth surface. The net result is positive feedback.
21.4.9. Biological CO2 Feedback
As plants grow, they consume CO2 to make hydrocarbons and carbohydrates via photosynthesis. As a result, the carbon is sequestered (stored) as the body of the plant. Some of the carbohydrates (e.g., sugars) are consumed by the plant, and are converted back to CO2 and transpired (exhaled by the plant) into the atmosphere.
When plants die and decay, or when they burn in a wild fire, they release their remaining carbon as CO2 back to the atmosphere. If plants are buried under sediment before they decay or burn, their carbon can be fossilized into coal, oil, natural gas (fossil fuels). Carbonate rocks can also sequester carbon from the atmosphere, but the carbon can later be released through weathering of the rocks.
The change of carbon from CO2 to other forms is called the global carbon cycle. It is extremely difficult to model the global carbon cycle, which leads to large uncertainty in estimates of climate feedback. Also, anthropogenic effects of fossil-fuel and biomass burning affect the cycle. At present, it is believed that biological CO2 causes a positive feedback. Namely, global warming will cause more CO2 to be released than sequestered.
Processes of abrupt climate change in Table 21-4 are left to the reader to explore (via an Evaluate & Analyze exercise).


