20.6: Nonlinear Dynamics and Chaos
- Page ID
- 9664
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)20.6.1. Predictability
In the late 1950s and early 1960s, Ed Lorenz was making numerical forecasts of convection to determine if statistical forecasts were better than NWP forecasts using the nonlinear dynamical equations. One day he re-ran a numerical forecast, but entered slightly different initial data. He got a strikingly different answer.
He was curious about this effect, and allowed himself to become sidetracked from his original investigations. This lead to his description of chaos, discovery of a strange attractor, and realization of the sensitive dependence of some equations to initial conditions.
He published his results in 1963 (“Deterministic non-periodic flow”. J. Atmos. Sci., 20, p 130-141). From 1963 to about 1975, this innovative paper was rarely cited by other scientists — a clue that it was not yet accepted by his colleagues. However, between 1975 and 1980, researchers became increasingly aware of his work. From 1980 to present, this paper has been cited on the order of 100 times per year.
About a decade and a half elapsed before this new theory gained wide acceptance, which is typical of many paradigm shifts. Namely, it takes about one human generation for a scientific revolution to mature, because typically the older scientists (who hold the power) are not willing to make the shift. The scientific revolution occurs when this group retires and younger scientists (with the newer ideas) take their place.
Recall that NWP is an initial-value problem, where these initial values are partially based on observed weather conditions. Unfortunately, the observations include instrumentation, sampling, and representativeness errors. We have already examined how such errors cause startup problems due to imbalanced flow conditions. How do these errors affect the long-range predictability?
Lorenz suggested that the equations of motion (which are nonlinear because they contain products of dependent variables, such as U and T in U·∆T/∆x) are sensitive to initial conditions. Such sensitivity means that small differences in initial conditions can grow into large differences in the forecasts.
This is unfortunate. Initial conditions will always have errors. Thus our forecasts will always become less accurate with increasing forecast time. Thus, there is a limit to the predictability of weather that is related to instability of the dynamics.
A simple physical illustration of sensitive dependence to initial conditions is a toy balloon. Inflate one with air and then let it go to fly around the room. Repeat the experiment, being careful to inflate the balloon the same amount and to point it in the same direction. You probably know from experience that the path and final destination of the balloon will differ greatly from flight to flight. In spite of how simple a toy balloon seems, the dynamical equations describing its flight are extremely sensitive to initial conditions, making predictions of flight path virtually impossible.
20.6.2. Lorenz Strange Attractor
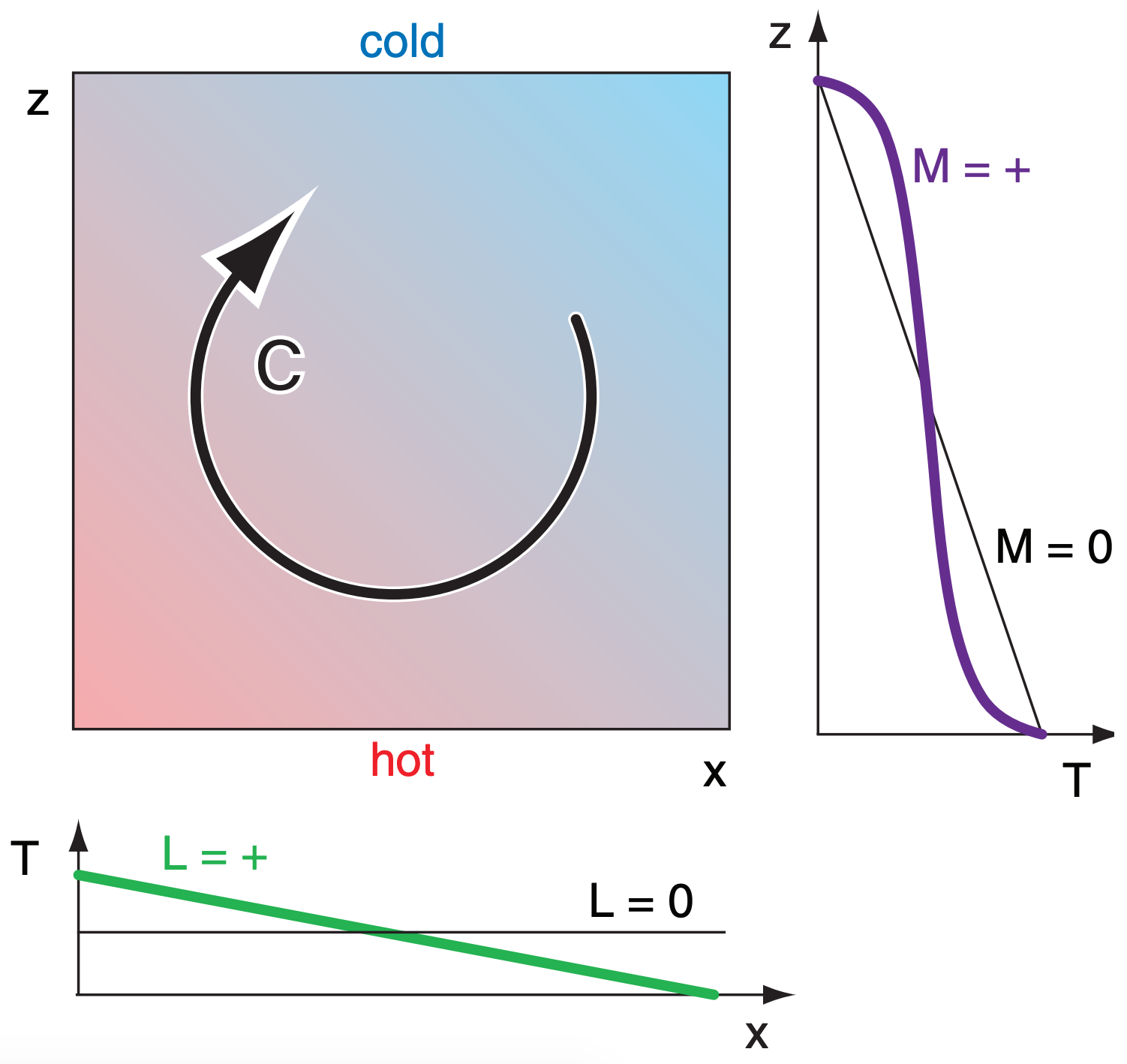
Another illustration of sensitive dependence to initial conditions was suggested by Lorenz. Suppose we examine 2-D convection within a tank of water, where the bottom of the tank is heated (Fig. 20.16). The vertical temperature gradient from bottom to top drives a circulation of the water, with warm fluid trying to rise. The circulation can modify the temperature distribution within the tank.
A very specialized, highly-simplified set of equations that approximates this flow is:
\begin{align}\begin{aligned}
&\frac{\Delta C}{\Delta t}=\sigma \cdot(L-C)\\
&\frac{\Delta L}{\Delta t}=r \cdot C-L-C \cdot M\\
&\frac{\Delta M}{\Delta t}=C \cdot L-b \cdot M
\end{aligned}\tag{20.23}\end{align}
where C gives the circulation (positive for clockwise, and greater magnitude for a more vigorous circulation), L gives the left-right distribution of temperature (positive for warm water on the left), and M indicates the amount of vertical mixing (0 for a linear temperature gradient, and positive when temperature is more uniformly mixed within the middle of the tank). Each of these dependent variables is dimensionless. Terms C·M and C·L are nonlinear.
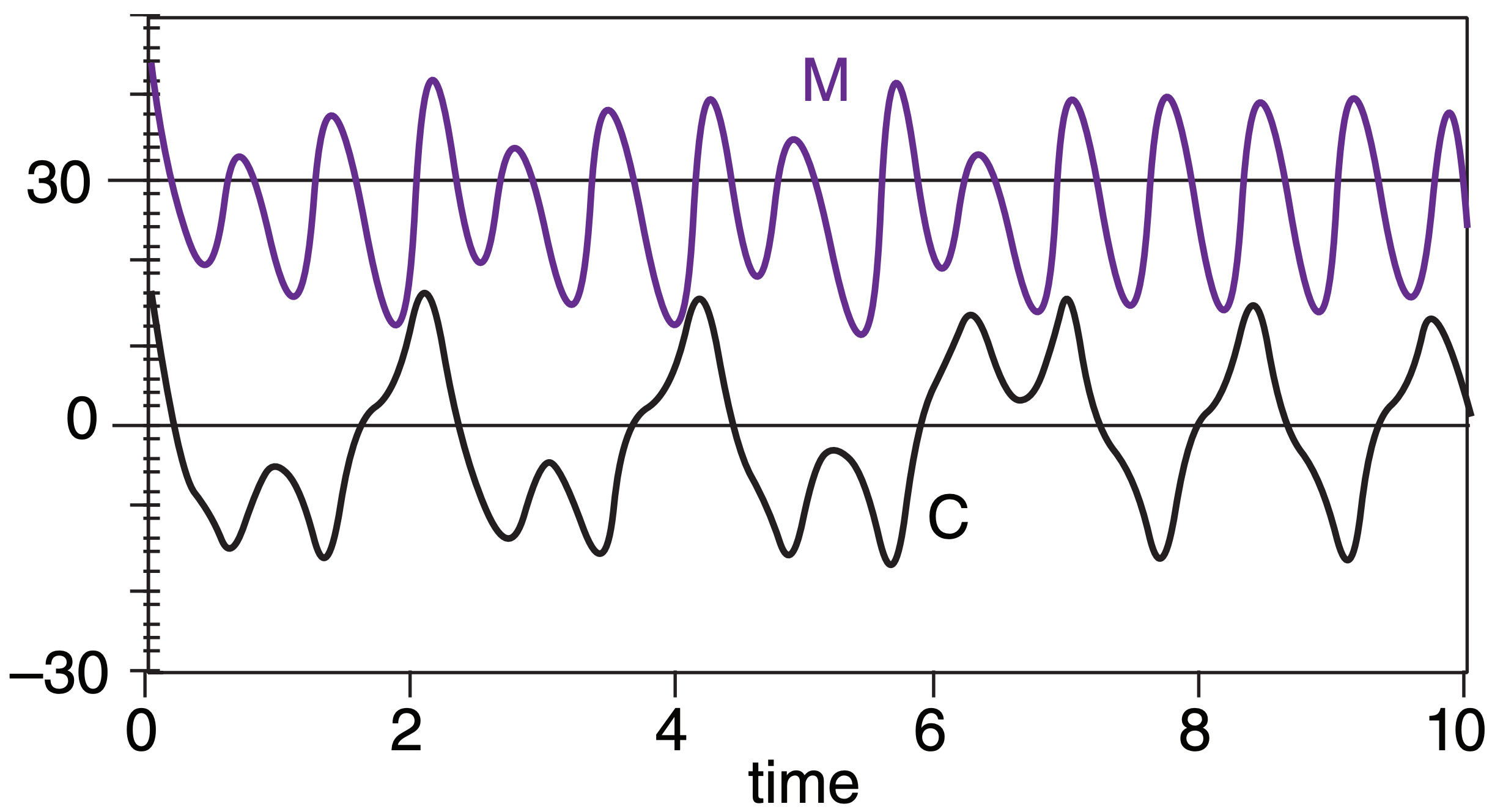
Fig. 20.17 shows forecasts of C and M vs. time, made with parameter values:
σ = 10.0, b = 8/3, and r = 28
and initial conditions:
C(0) = 13.0, L(0) = 8.1, and M(0) = 45.
Note that all three variables were forecast together, even though L was not plotted to reduce clutter. From Fig. 20.17 it is apparent that the circulation changes direction chaotically, as indicated by the change of sign of C. Also, the amount of mixing in the interior of the tank increases and decreases, as indicated by chaotic fluctuations of M.
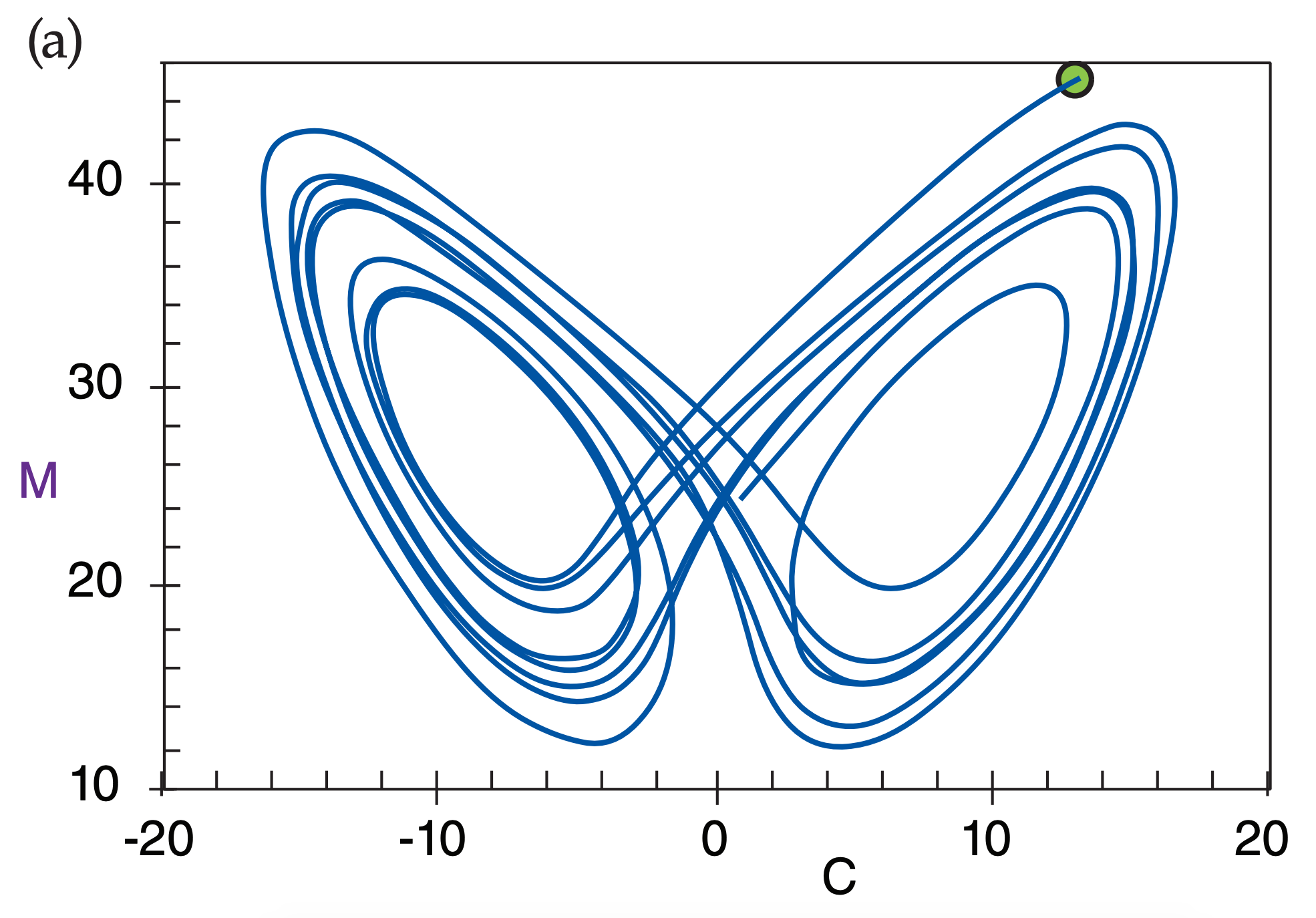

When one dependent variable is plotted against another, the result is a phase-space plot of the solution. Because the Lorenz equations have three dependent variables, the phase space is three-dimensional. Figs. 20.18 shows two-dimensional views of the solution, which looks like a butterfly.
This solution exhibits several important characteristics that are similar to the real atmosphere. First, it is irregular or chaotic, meaning that it is impossible to guess the solution in the future. Second, the solution is bounded within a finite domain:
–20 < C < 20, –30 < L < 30, 0 ≤ M < 50.
which implies that the solution will always remain physically reasonable.
Third, the solution (M vs. C) appears to flip back and forth between two favored regions, (i.e., the separate wings of the butterfly). These wings tend to attract the solution toward them, but in a rather strange way. Hence, they are called strange attractors.
Fourth, the exact solution is very dependent on the initial conditions, as illustrated in the Sample Applications next. Yet, the eventual solution remains attracted to the same butterfly.
The atmosphere has many more degrees of freedom (i.e., is more complex) than the simple Lorenz model. So we anticipate that the atmosphere is intrinsically unpredictable due to its nonlinear chaotic nature. In other words, there is a limit to how well we can predict the weather.
Sample Application (§)
Solve the Lorenz equations for the parameters and initial conditions listed previously in this chapter. Use a dimensionless time step of ∆t = 0.01, and forecast from t = 0 to t = 10.
Find the Answer
Given: C(0) = 13.0, L(0) = 8.1, and M(0) = 45, and σ = 10.0, b = 8/3, and r = 28.
Find: C(t) = ?, L(t) = ?, M(t) = ?
First, rewrite eqs. (20.23) in the form of a forecast:
\(\ \begin{aligned}
&C(t+\Delta t)=C(t)+\Delta t \cdot[\sigma \cdot(L(t)-C(t))]\\
&L(t+\Delta T)=L(t)+\Delta t \cdot[r \cdot C(t)-L(t)-C(t) \cdot M(t)]\\
&M(t+\Delta T)=M(t)+\Delta t \cdot[C(t) \cdot L(t)-b \cdot M(t)]
\end{aligned}\)
As an example, for the 1st step: C(0.01) = 13.0 + 0.01·[10.0·(8.1-13.0)] = 12.51
Next, set this up on a spreadsheet, a portion of which is reproduced below.
| t | C | L | M |
| 0.00 | 13.00 | 8.1 | 45.00 |
| 0.01 | 12.51 | 5.809 | 44.85 |
| 0.02 | 11.84 | 3.643 | 44.38 |
| 0.03 | 11.02 | 1.666 | 43.63 |
| 0.04 | 10.08 | -0.07 | 42.65 |
| 0.05 | 9.069 | -1.55 | 41.51 |
| 0.06 | 8.007 | -2.76 | 40.26 |
| 0.07 | 6.931 | -3.71 | 38.96 |
| 0.08 | 5.866 | -4.44 | 37.67 |
| 0.09 | 4.836 | -4.96 | 36.4 |
| 0.10 | 3.856 | -5.32 | 35.19 |
Note that your answers might be different than these, due to different round-off errors and mathematical libraries on the spreadsheets.
Plots. These answers are already plotted in Figs. 20.17 - 20.18.
Check: Units dimensionless. Physics OK.
Exposition: The forecast equations above use an Euler time-differencing scheme, which is the least accurate. Nevertheless, it illustrates the Lorenz attractor.
Sample Application (§)
Repeat the previous Sample Application, but for a slightly different initial condition: M(0) = 44.
Find the Answer
Given: C(0) = 13.0, L(0) = 8.1, and M(0) = 44, and σ = 10.0, b = 8/3, r = 28.
Find: C(t) = ?, L(t) = ?, M(t) = ?
As in the previous Sample Application.
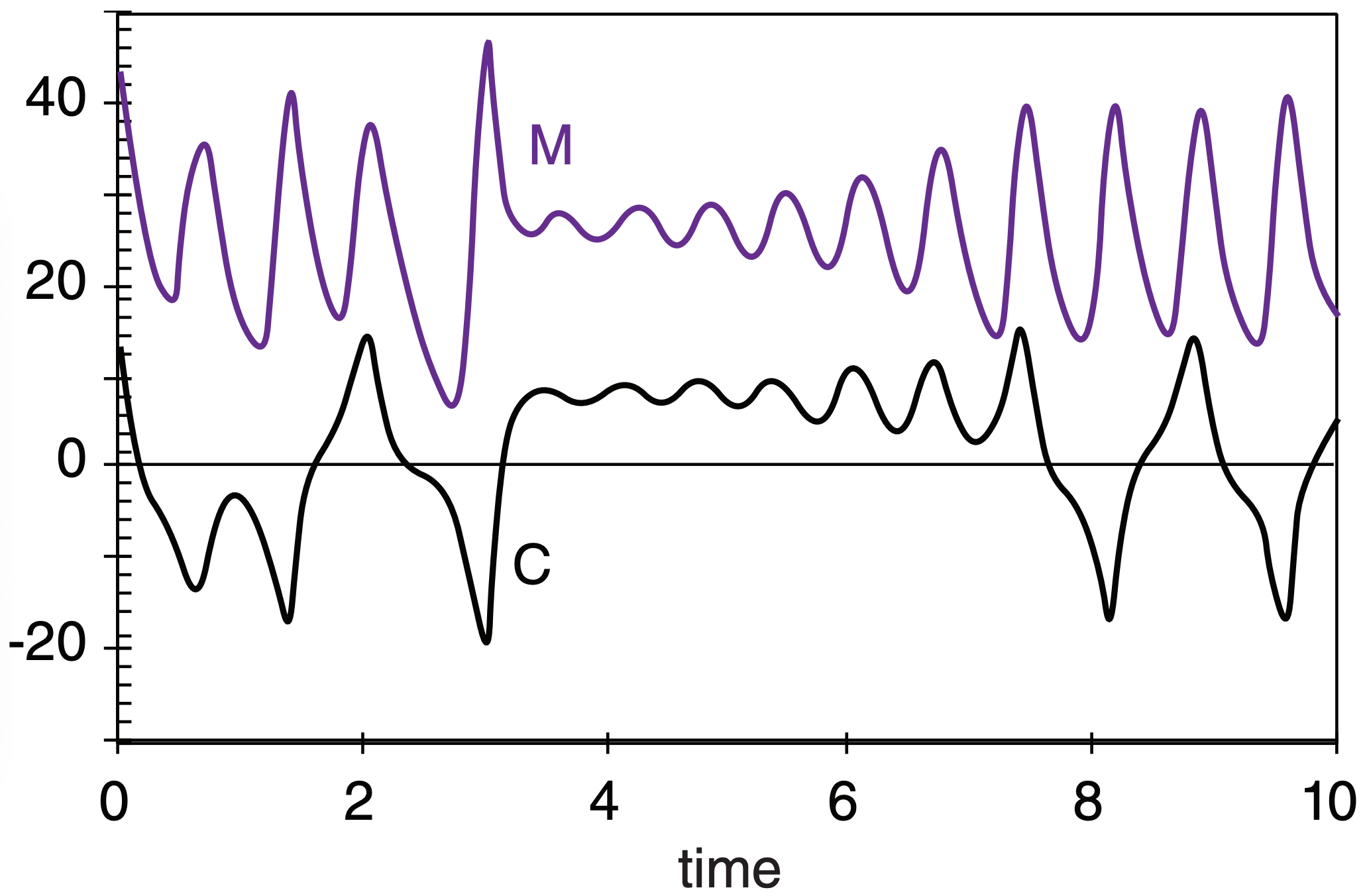

Check: Units OK. Physics OK.
Exposition: These are quite different from Figs. 20.17 & 20.18, demonstrating sensitive dependence to initial conditions.
Sensitive Dependence on Initial Conditions
“Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?” – E. Lorenz & P. Merilees, 1972.
“Can a man sneezing in China cause a snow storm in New York? – George R. Stewart, 1941: Storm.
“Did the death of a prehistoric butterfly change the outcome of a US presidential election?” – Ray Bradbury, 1952, 1980, A Sound of Thunder.
“Computations indicate that a perfect model should produce:
- three-day forecasts ... which are generally good;
- one-week forecasts ... which are occasionally good;
- and two-week forecasts ... which, although not very good, may contain some useful information”
– E. Lorenz, 1993: The Essence of Chaos. Univ. of Washington Press, Seattle. 227 pp.
20.6.3. Ensemble Forecasts
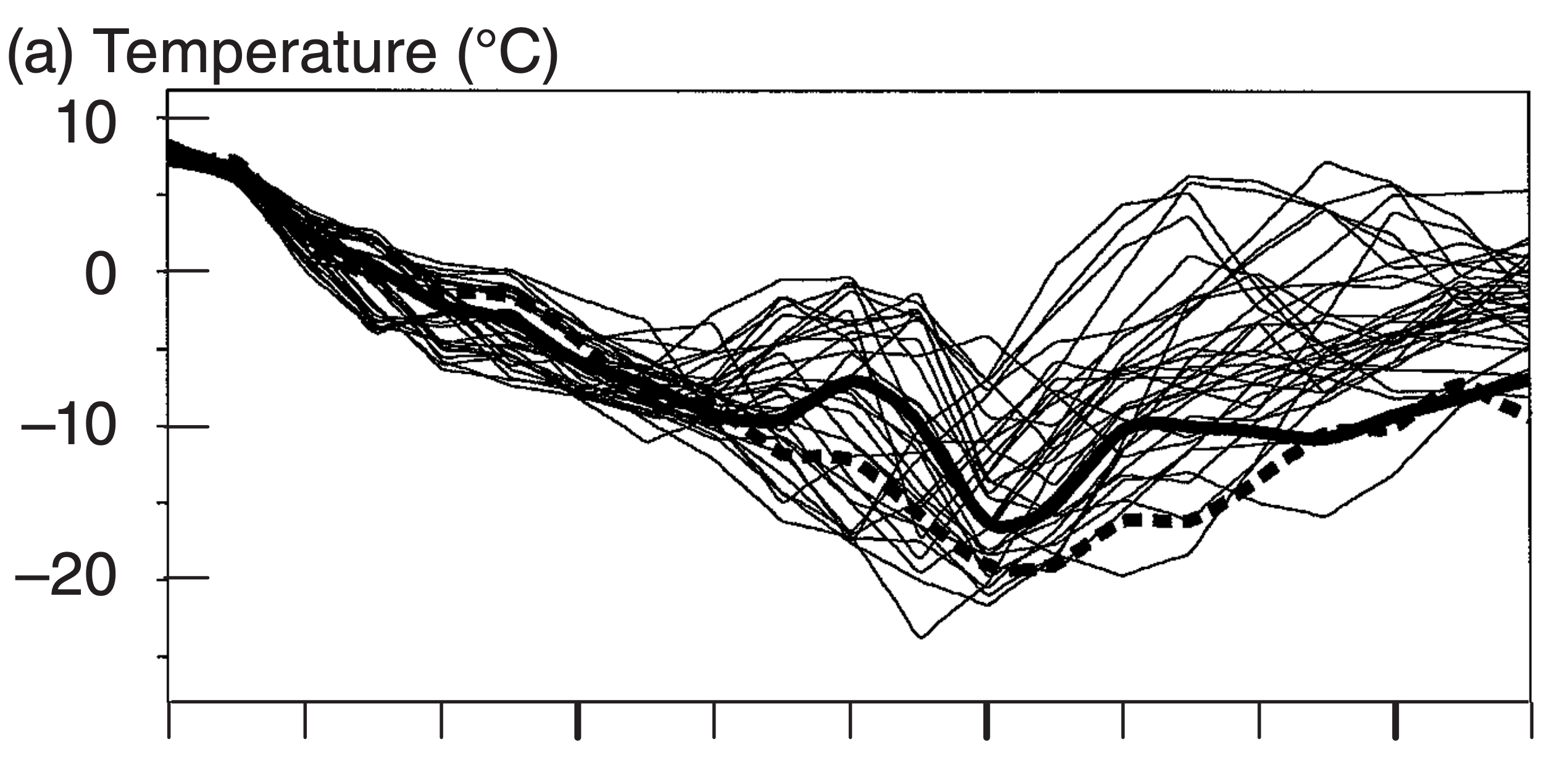
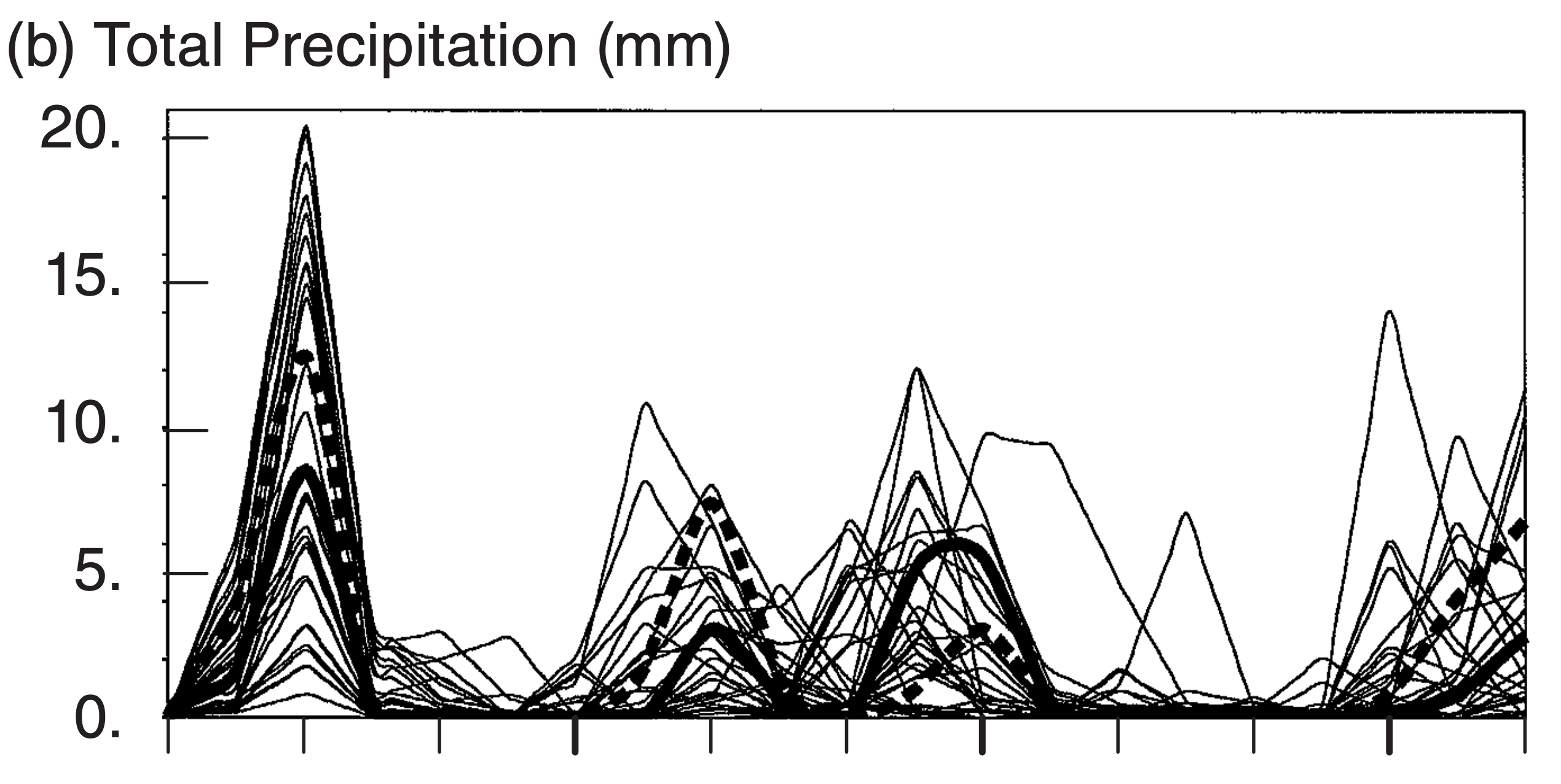
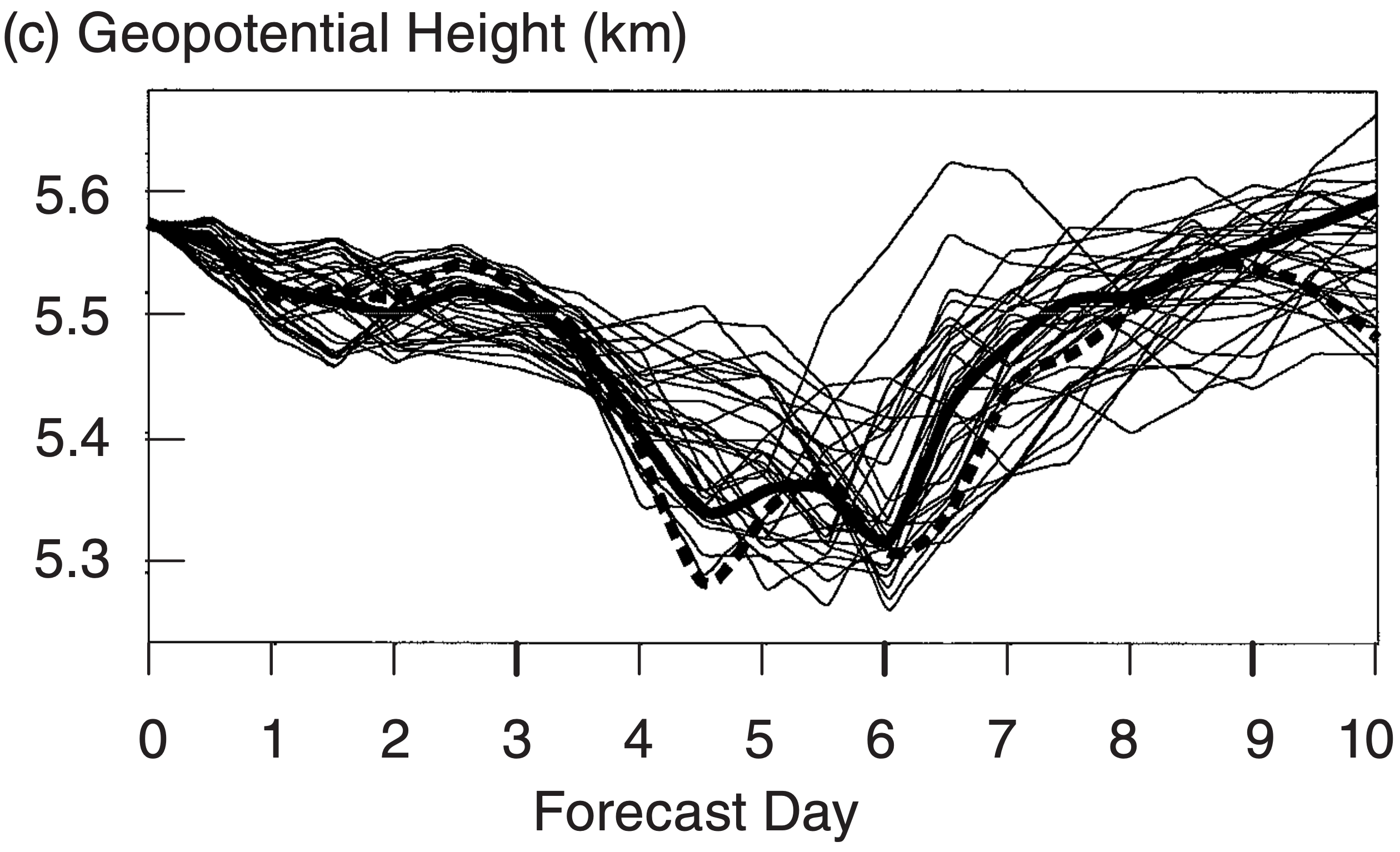
Some forecast centers repeatedly forecast the same time period, but for different conditions. These differences can be created by using different initial conditions, physical parameterizations, numerics, and/or NWP models. Such a procedure yields an ensemble of forecasts that reveals the sensitive dependence of weather forecasts on those different conditions. Fig. 20.19 shows 10-day ensemble forecasts of 85-kPa temperature, precipitation, and 50- kPa geopotential heights at Des Moines, Iowa, for the same case-study period as discussed previously.
The heavy dotted line in these figures shows the single forecast run made with the high-resolution model, starting from the “best” initial conditions. This is the “official” forecast produced by ECMWF. The thick solid line starts from the same initial conditions, but is made with a coarser grid resolution to save forecast time. Note that the forecast changes substantially when the grid resolution changes.
The thin lines are forecasts from slightly different initial conditions. To save computer time, these multiple forecasts are also made with the lower grid resolution. The forecasts of temperature and geopotential height start out quite close, and diverge slowly during the first 3.5 days. At that time (roughly when the cyclone reaches Des Moines late 22 Feb 94), the solution rapidly diverges, signaling a sudden loss in forecast skill that is never regained.
The spread of the ensemble members informs you about the uncertainty of the forecast. Unfortunately, you have no way of knowing which of the ensemble members will be closest to reality.
By averaging all the ensemble members together, you can find an ensemble average forecast that is usually more skillful than any individual member. This is one of the strengths of ensemble forecasting.
After several days into the forecast (Fig. 20.19), the ensemble forecasts seem chaotic. Yet this chaotic solution is bounded within a finite region — perhaps a “strange attractor” such as studied by Lorenz.
Studies of chaos often focus on the eventual state of the solution, at times far from the initial condition. At these long times, the dynamics have forgotten the initial state. Although this eventual state is somewhat useless as a weather forecast, it can provide some insight into the range of possible climatic conditions that are allowed by the dynamical equations in the model (i.e., the model’s climate).
Ensemble forecasts can also suggest which conditions are unlikely — valuable information for some users. For example, if none of the ensemble forecasts give temperatures below freezing on a particular day, then a categorical “no-freeze” forecast could be made. Better confidence in such forecasts is possible by calibrating the ensemble spread into a probabilistic forecast, discussed next.
20.6.4. Probabilistic Forecasts
Due to the inherent unpredictability of the atmosphere, we cannot confidently make deterministic forecasts such as “the temperature tomorrow at noon will be exactly 19.0°C”. However, it is possible to routinely create probabilistic forecasts similar to “there is a 60% chance the temperature tomorrow at noon will be between 18°C and 20°C, and an 80% chance the it will be between 16 and 22°C.”
Ensemble forecasts are increasingly used to create probabilistic forecasts. Various methods can be used to convert the distribution of ensemble members into raw probability forecasts. The raw probabilities are then calibrated (Fig. 20.20) to make them sharp (deviating from climatology) and reliable (forecast probabilities match observation frequencies).
The spread of the probability distribution (i.e., the uncertainty in the forecast) depends on the season (greater spread in winter), the location (greater spread downwind of data-void regions), the climate (greater spread in parts of the globe where weather is more variable), and on the accuracy of the NWP models. A perfect forecast would have no spread.
Often, probability forecasts are given as a cumulative probability CP that some threshold will be met or exceeded. In Fig. 20.20, the lowest solid line represents a cumulative probability of CP = 10% (there is a 10% chance that the observed wind speed will be slower than this forecast speed) and the highest solid line is for CP = 90% (there is a 90% chance that the observation will be slower than this other forecast speed).



