16.4: Dynamics
- Page ID
- 9634
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)16.4.1. Origin of Initial Rotation
Define absolute angular momentum (AAM) as the sum of a relative component of angular momentum associated with tropical-cyclone rotation plus a background component due to the rotation of the Earth:
\[ \begin{align} A A M=M_{\tan } \cdot R+0.5 \cdot f_{c} \cdot R^{2}\label{16.1}\end{align}\]
where the Coriolis parameter is fc (≈ 0.00005 s–1 at 20° latitude), and the tangential component of velocity at distance R from the eye center is Mtan.
As near-surface air converges toward the weak low-pressure of an incipient tropical cyclone, absolute angular momentum is conserved for frictionless flow (i.e., for no drag against the sea surface). Eq. (16.1) indicates that there is nonzero AAM even if the incipient tropical cyclone has no rotation yet (i.e., even if Mtan.initial = 0). Equating the resulting initial AAM for air starting at distance Rinit from the eye center, with the final AAM after the air has moved closer to the eye (i.e., smaller Rfinal ) yields:
\[ \begin{align} M_{\mathrm{tan}}=\frac{f_{c}}{2} \cdot\left(\frac{R_{\text {init}}^{2}-R_{\text {final}}^{2}}{R_{\text {final}}}\right)\label{16.2}\end{align}\]
For real tropical cyclones you should not neglect frictional drag. Thus, you should anticipate that actual winds will be slower than given by eq. (16.2).
The Canadian East Coast only rarely gets hurricanes — one every 3 to 4 years on average. But it gets many former hurricanes that have weakened to Tropical Storm or lower categories during passage over the cold Labrador current (for Atlantic Canada), or due to passage over land (for Central Canada).
On 29 Sep 2003, Hurricane Juan hit Nova Scotia, Canada, as a category 2 hurricane. Two factors made this possible: (1) warm (but colder than 26.5°C) seasurface water was relatively close to Nova Scotia; and (2) the hurricane was translating north so quickly that it did not have time to spin down over the narrow cold-water region before making landfall.
This storm began as Tropical Depression #15 about 470 km southeast of Bermuda at noon on 25 Sep. Six hours later it became a Tropical Storm, and by noon 26 Sep it became a Hurricane while 255 km east of Bermuda. During the next 3 days it traveled northward over the Gulf Stream, with intensity of category 2 for most of its journey.
When it reached Canada, it dropped 25 to 40 mm of rain in Nova Scotia. The storm surge was 1.5 m, and the maximum wave height was roughly 20 m. Hundreds of thousands of people lost electrical power due to trees falling on power lines, and 8 people were killed in storm-related accidents.
Before Juan, the most remembered “former hurricane” to strike Canada was Hurricane Hazel. It transitioned into a strong extratropical cyclone before reaching Canada, but caused 81 deaths and severe flooding in southern Ontario in mid October 1954.
Since 1887, there have been two hurricanes of category 3, five of category 2, and 26 of category 1. Info about Canadian hurricanes is available from the Canadian Hurricane Centre, Halifax, Nova Scotia.
16.4.2. Subsequent Spin-up
As the winds accelerate around a strengthening tropical cyclone, centrifugal force increases. Recall from the Atmospheric Forces & Winds chapter that the equation for gradient-wind in cylindrical coordinates (eq. 10.32) is:
\(\ \begin{align} \frac{1}{\rho} \cdot \frac{\Delta P}{\Delta R}=f_{c} \cdot M_{\tan }+\frac{M_{\tan }^{2}}{R}\label{16.3}\end{align}\)
where air density is ρ and the pressure gradient in the radial direction is ∆P/∆R. In eq. (16.3) the last term gives the centrifugal force. The gradient wind applies at all radii from the center of the storm, and at all altitudes except near the bottom (in the boundary layer) and near the top (in the anvil or cirrus shield region).
Some researchers find it convenient to neglect Coriolis force closer to the center of the stronger tropical cyclones where the winds are faster. For this situation, the tangential tropical cyclone winds can be crudely approximated by the cyclostrophic wind, Mcs (see the Atmospheric Forces & Winds Chapter):
\(\ \begin{align} M_{c s}=M_{\tan }=\sqrt{\frac{R}{\rho} \cdot \frac{\Delta P}{\Delta R}}\label{16.4}\end{align}\)
Nonetheless, the gradient-wind equation (16.3) is the most appropriate equation to use for tropical cyclones, at middle altitudes of the storm.
Sample Application
Suppose that air at a latitude of 12° initially has no rotation as it is drawn toward a low-pressure center 500 km away. When the air reaches 200 km from the low center, what will be its relative tangential velocity?
Find the Answer
Given: Rinit = 500 km, ϕ = 12°, Rfinal = 200 km
Find: Mtan = ? m s–1
Compute the Coriolis parameter:
fc = 2·ω·sin(ϕ) = (1.458x10–4 s–1)·sin(12°) = 0.0000303 s–1
Use eq. (16.2):
\(M_{tan} =\frac{\left(0.0000303 s^{-1}\right)}{2} \cdot\left(\frac{(500 k m)^{2}-(200 k m)^{2}}{200 k m}\right)=\underline{\mathbf{15.9 m s^{-1}}}\)
Check: Units OK. Physics OK.
Exposition: This is halfway toward the 32 m s–1 that defines a Category 1 tropical cyclone. Tropical cyclones cannot exist at the equator because fc = 0 there.
Sample Application
Given a tropical cyclone with: sea-level pressure difference between the eye and far outside of ∆Pmax = 11.3 kPa, eyewall outside radius of Ro = 25 km, latitude = 14°N, and ρ = 1 kg m–3. From the tropical cyclone model presented later in this chapter, assume the pressure gradient is roughly: ∆P/∆R =(4/5)·∆Pmax/Ro .
a) Find the magnitude of the gradient wind just outside of the eye wall (i.e., at R = Ro) .
b) Compare the relative importance of the Coriolis and centrifugal terms in the gradient wind eq.
c) Compare this gradient wind with the max expected surface wind of 67 m s–1, and explain any difference.
Find the Answer
Given: ∆Pmax = 11.3 kPa, Ro = 25 km, latitude = 14°N, ρ = 1 kg m–3.
Find: Mtan = ? m s–1. Compare terms.
a) Use: ∆P/∆R =(4/5)·∆Pmax/Ro
Find fc = (1.458x10–4 s–1)·sin(14°) = 3.5x10–5 s–1 .
Use eq. (16.3) and neglect translation speed:
\(\frac{(4 / 5)}{\rho} \cdot \frac{\Delta P_{\max }}{R_{o}}=f_{c} \cdot M_{\tan }+\frac{M_{\tan }^{2}}{R}\)
Pressure Gradient = Coriolis + Centrifugal
Using trial and error (i.e., trying different values of Mtan in a spreadsheet until the left and right sides of the eq balance): Mtan = 94.65 m s–1.
b) From my spreadsheet, the terms in the eq. are:
0.361 = 0.003 + 0.358
Pressure Gradient = Coriolis + Centrifugal
Thus, the Coriolis force is about 2 orders of magnitude smaller than centrifugal force, at this location of strongest tangential wind just outside the eye wall. At this location, the cyclostrophic assumption (of neglecting Coriolis force) is OK.
c) The max expected surface wind of 67 m s–1 includes the effect of drag against the sea surface, which is why it is smaller than our answer from (a) Mtan = 95 m s–1.
Check: Units OK. Physics OK.
Exposition: This scenario is similar to the composite tropical cyclone model presented later in this chapter.
Sample Application
Suppose a tropical cyclone has a pressure gradient of 1 kPa/15 km at radius 60 km. What is the value of the cyclostrophic wind? Given ρ = 1 kg m–3.
Find the Answer
Given: R = 60 km, ∆P = 1 kPa, ∆R = 15 km,
Find: Mcs = ? m s–1
Use eq. (16.4):
\(M_{c s}=\sqrt{\frac{(60 \mathrm{km})}{\left(1 \mathrm{kg} \cdot \mathrm{m}^{-3}\right)} \cdot \frac{(1000 \mathrm{Pa})}{(15 \mathrm{km})}}=\underline{\mathbf{63 ms^{-1}}}\)
Check: Physics & Units OK.
Exposition: This is a Category 4 tropical cyclone.
16.4.3. Inflow and Outflow
At the bottom of the tropical cyclone (Fig. 16.24), drag against the sea surface causes the winds to spiral in towards the eyewall. The boundary-layer gradient wind equation (see the Atmospheric Forces & Winds chapter) describes this flow well. Without this drag-related inflow, the eyewall thunderstorms would not get sufficient warm humid air to survive, causing the tropical cyclone to die.
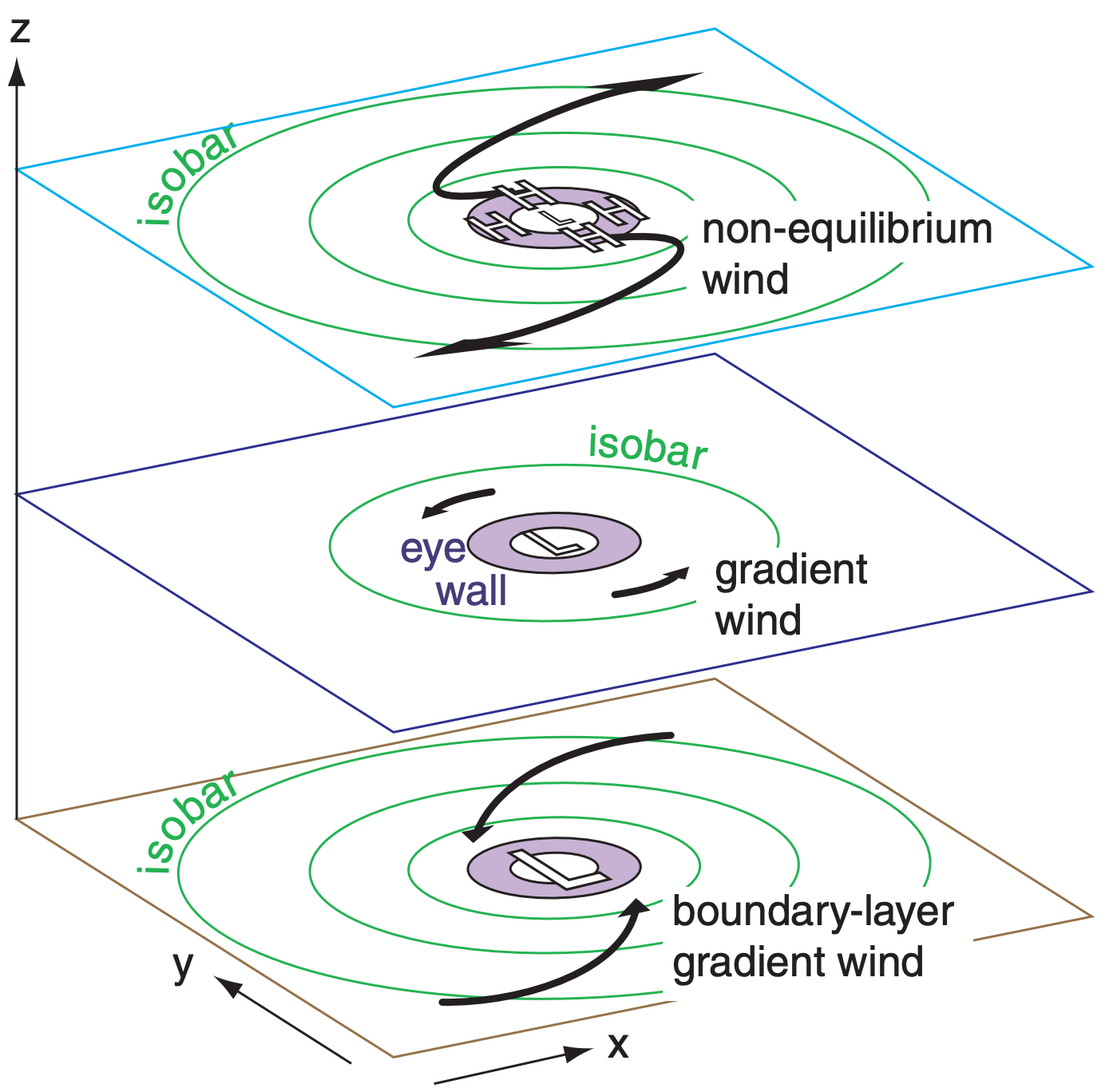
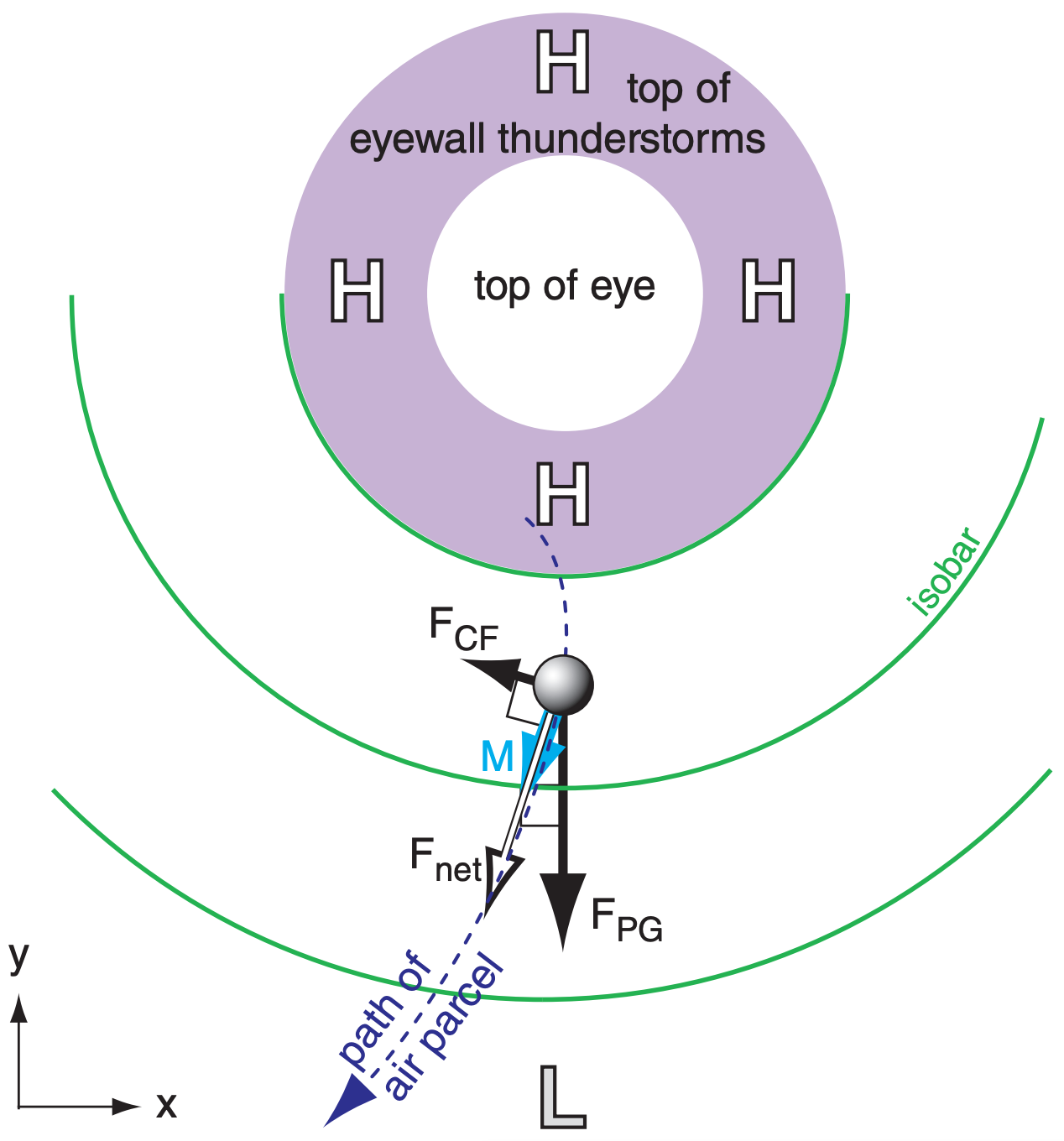
Explaining the outflow at the top of a tropical cyclone is trickier, because drag forces are so small that we cannot invoke the boundary-layer gradient-wind equation. One important process is the rapid upward movement of air by thunderstorm updrafts in the eyewall, which deposits enough air molecules at the top of the storm to contribute to high pressure there. Thus, the outflow is related to two factors:
- The cyclonically-moving air from the boundary layer is brought to the top of the tropical cyclone by eyewall-thunderstorm updrafts so quickly that its inertia prevents it from instantly changing to anticyclonic outflow. Namely, the outflow is initially moving the wrong way (cyclonically) around the high (Fig. 16.24). The outflow must change direction and increase its speed, and thus is not in steady state.
- It is physically impossible to create a balanced gradient-wind flow around a high-pressure area that is surrounded by an excessively strong pressure gradient, as was explained in the Atmospheric Forces & Winds chapter (also see HIGHER MATH in the next column). But the thunderstorm updrafts help create such an excessive high pressure at storm top that the pressure-gradient force exceeds the compensating Coriolis force (Fig. 16.25). The result is a net outward force that causes the air to accelerate outward from the eyewall as a non-equilibrium wind.