14.4: Instability, Cape and Updrafts
- Page ID
- 9620
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The second requirement for convective-storm formation is instability in the pre-storm sounding. Nonlocal conditional instability (NCI) occurs when warm humid atmospheric boundary layer (ABL) air is capped by a temperature inversion, above which is relatively cold air. The cold air aloft provides an environment that gives more buoyancy to the warm updraft air from below, allowing stronger thunderstorms. The “nonlocal” aspect arises because air from below the cap becomes unstable above the cap. The “condition” is that the ABL air must first be lifted past the cap (i.e., past its LCL and LFC) for the instability to be realized.
The capping inversion traps the warm humid air near the ground, allowing sensible and latent heat energy to build up during the day as the sun heats the ground and causes evaporation. Without this cap, smaller cumulus clouds can withdraw the warm humid air from the boundary layer, leaving insufficient fuel for thunderstorms. Thus, the cap is important — it prevents the fuel from leaking out.
The US Storm Prediction Center has found some clues for thunderstorm intensity based on the lifting condensation level (LCL) and the level of free convection (LFC):
- Tornadoes are more likely when zLFC < 2 km agl.
- Thunderstorms are more easily triggered and maintained when zLFC < 3 km agl.
- Deep convection is more likely when zLFC – zLCL is smaller.
where agl = above ground level.
14.4.1. Convective Available Potential Energy
Thunderstorms get their energy from the buoyancy associated with latent-heat release when water vapor condenses. The Convective Available Potential Energy (CAPE) is a way to estimate this energy using a thermo diagram. CAPE is proportional to the shaded area in Fig 14.34; namely, the area between LFC and EL altitudes that is bounded by the environmental sounding and the moist adiabat of the rising air parcel.

To explain this, you can use the definition of buoyancy force per unit mass \(F / m=|g| \cdot\left(T_{v p}-T_{v e}\right) / T_{v e}\) that was covered in the Atmospheric Stability chapter. \(T_{v p}\) is the virtual temperature of the air parcel rising in the thunderstorm, \(T_{v e}\) is virtual temperature in the surrounding environment at the same altitude as the thunderstorm parcel, and |g|= 9.8 m s–2 is gravitational acceleration magnitude.
Recall from basic physics that work equals force times distance. Let (∆E/m) be the incremental work per unit mass associated with a thunderstorm air parcel that rises a small increment of distance ∆z. Thus, ∆E/m = (F/m)· ∆z , or:
\(\ \begin{align} \frac{\Delta E}{m} \cong \Delta z \cdot|g| \frac{\left(T_{v p}-T_{v e}\right)}{T_{v e}}\tag{14.1}\end{align}\)
Recall from Chapter 1 that virtual temperature includes the effects of both water vapor and liquid water. Water vapor is less dense than air (Tv > T), thus increasing the buoyant energy. Liquid- and solid-water hydrometeors (cloud droplets, rain, and snow) falling at their terminal velocity are heavier than air (Tv < T), thus decreasing the upward buoyant energy. Both are important for thunderstorms, but are often difficult to determine.
Instead, you can use the approximation Tv ≈ T, which gives:
\(\ \begin{align} \frac{\Delta E}{m} \cong|g| \frac{\Delta z \cdot\left(T_{p}-T_{e}\right)}{T_{e}}=|g| \cdot(\text {Increm.Area}) / T_{e}\tag{14.2}\end{align}\)
where Tp is air-parcel temperature, Te is environmental temperature, and the incremental area (Increm. Area) is shown Fig. 14.35 as the dark-red rectangle.
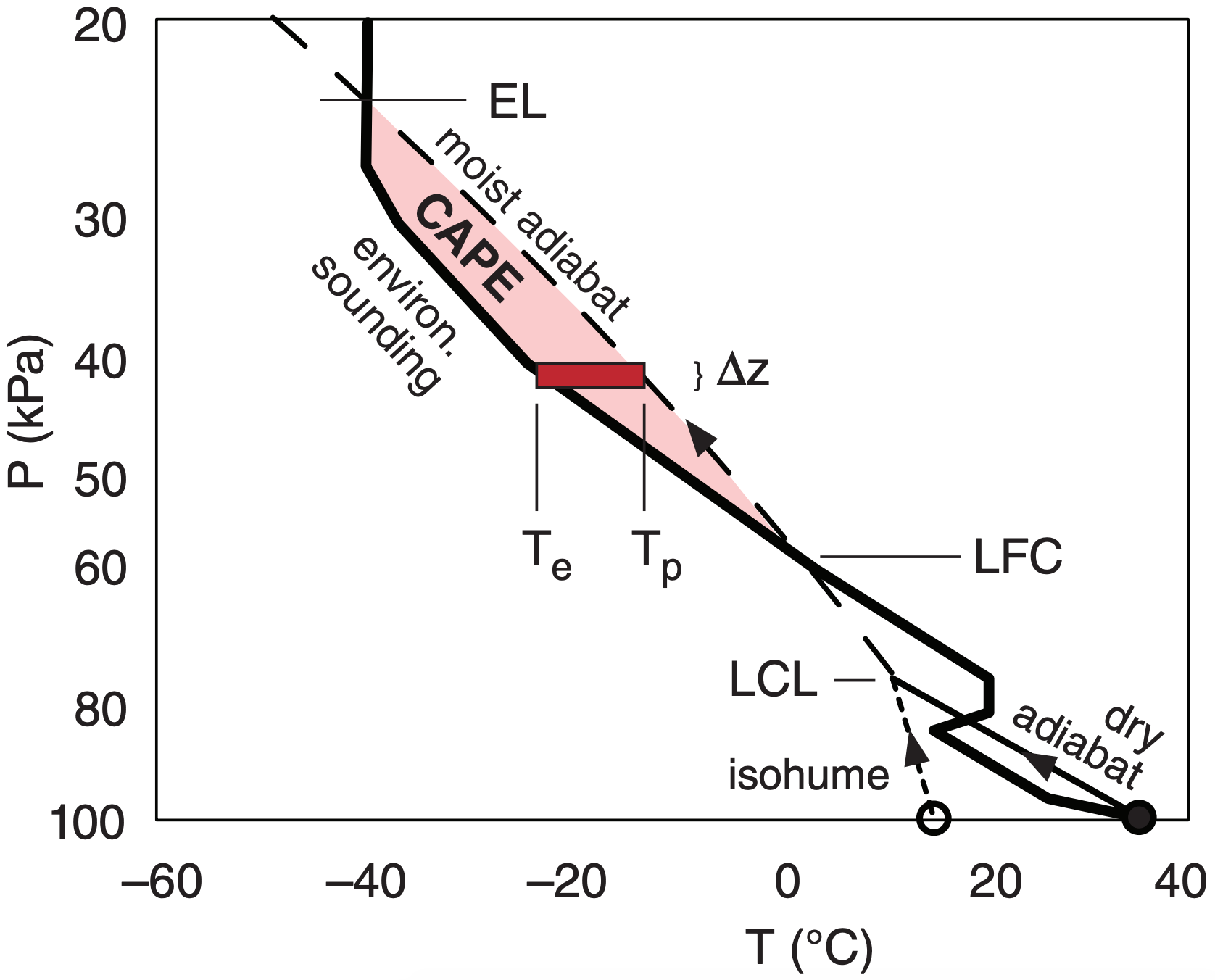
Adding all the incremental rectangles between the LFC and the EL gives a total area (light shading in Fig. 14.35) that is proportional to CAPE.
\(\ \begin{align} C A P E \cong|g| \cdot(\text {Total.Area}) / T_{e}\tag{14.3}\end{align}\)
or
\(\ \begin{align} C A P E \cong|g| \sum_{L F C}^{EL}\left(T_{p}-T_{e}\right) \cdot \Delta z / T_{e}\tag{14.4}\end{align}\)
The units of CAPE are J·kg–1. These units are equivalent to m2·s–2 ; namely, velocity squared. The temperature in the denominator of eqs. (14.3 & 14.4) must be in Kelvin. Both numerator temperatures must have the same units: either Kelvin or °C.
The shape of the CAPE area is usually not simple, so calculating the area is not trivial. At severeweather forecast centers, computers calculate CAPE automatically based on the pre-storm sounding. By hand, you can use a simple graphical method by first plotting the sounding and the surface-parcel rise on a thermo diagram, and then using whatever height and temperature increments are plotted on the background diagram to define “bricks” or “tiles”, each of known size.
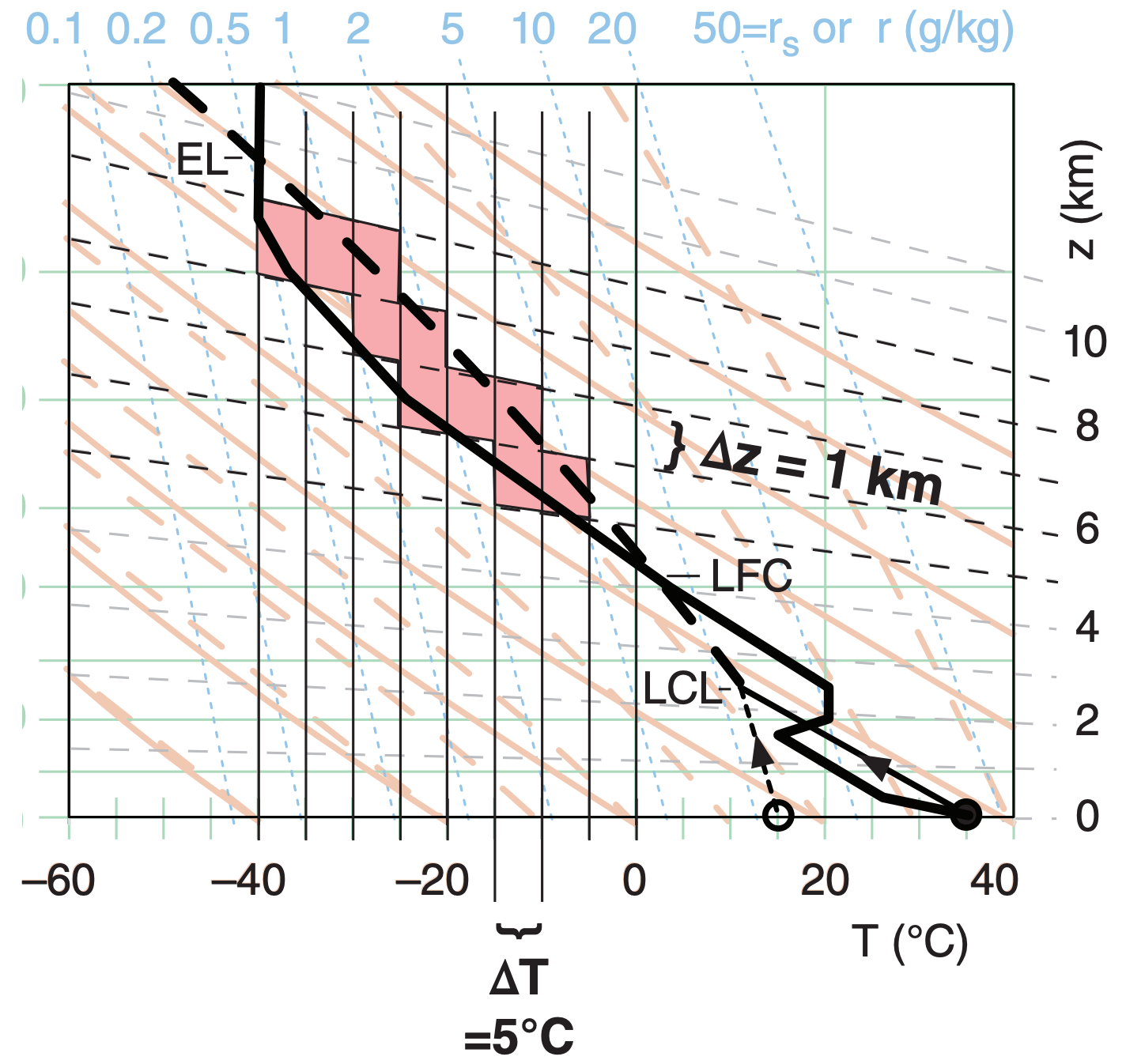
Namely, instead of using long narrow rectangles, each of different width, as sketched in Fig. 14.35, you can cover the complex shaded area with smaller, non-overlapping tiles, each of equal but arbitrary size ∆T by ∆z (such as ∆T = 5°C and ∆z = 1 km, see Fig. 14.36). Count the number of tiles, and multiply the result by the area of each tile (∆T·∆z = 5 °C·km in this example). When tiling the CAPE area, try to compensate for small areas that are missed by the tiles by allowing some of the other tiles to extend slightly beyond the boundaries of the desired shaded area by roughly an equal area (e.g., see the Sample Application). Smaller-size tiles (such as ∆T = 1°C and ∆z = 0.2 km) give a more accurate answer (and are recommended), but are more tedious to count.
Sample Application
For the sounding in Fig 14.36, estimate the CAPE.
Find the Answer
Given: Fig 14.36.
Find: CAPE = ? J·kg–1
Each tile has size ∆T = 5°C by ∆z = 1000 m. The area of each tile is 5,000 °C·m, and there are 10 tiles. The total area is: Area = 10 x 5000 °C·m = 50,000 K·m , [where I took advantage of ∆T(°C) = ∆T(K) ].
By eye, the average Te in the CAPE region is about –25°C = 248 K. Use eq. (14.3):
CAPE = [ 9.8 m·s–2 / 248K ]·(50,000 K·m) = = 1976 m2·s–2 = 1976 J·kg–1.
Check: Physics and units OK. Figure OK.
Exposition: This is a moderate value of CAPE that could support supercell storms with tornadoes.
On many thermo diagrams such as the emagram of T vs. ln(P) used here, the height contours and isotherms are not perpendicular; hence, the rectangles look like trapezoids (see the Sample Application that employed Fig. 14.36). Regardless of the actual area within each trapezoid in the plotted graph, each trapezoid represents a contribution of ∆T by ∆z toward the total CAPE area.
To replace heights with pressures in the equation for CAPE, use the hypsometric equation from Chapter 1, which yields:
\(\ \begin{align} C A P E=\mathfrak{R}_{d} \cdot \sum_{L F C}^{E L}\left(T_{p}-T_{e}\right) \cdot \ln \left(\frac{P_{\text {bottom}}}{P_{\text {top}}}\right)\tag{14.5}\end{align}\)
where ℜd = 287.053 J·K–1·kg–1 is the gas constant for dry air, Pbottom and Ptop are the bottom and top pressures of the incremental rectangle, and the sum is still over all the rectangles needed to tile the shaded CAPE area on the sounding (Fig. 14.37). Again, the temperature difference in eq. (14.5) in °C is equal to the same value in Kelvin.

All of the CAPE figures up until now have followed a rising air parcel that was assumed to have started from near the surface. This is called Surface-Based CAPE (SBCAPE), which is often a good method for the mid-afternoon pre-storm soundings that have been shown so far.
Sample Application
For the sounding in Fig. 14.37, estimate the CAPE using pressure rather than height increments.
Find the Answer
Given: Fig. 14.37
Find: CAPE = ? J·kg–1
Use eq. (14.5):
CAPE = [287 J/(K·kg)] · { [ –30°C – (–40°C)] · ln(30kPa/25kPa)] + [ –24°C – (–33°C)] · ln(35kPa/30kPa)] + [ –17°C – (–27°C)] · ln(40kPa/35kPa)] + [ –12°C – (–20°C)] · ln(45kPa/40kPa)] + [ –7°C – (–13°C)] · ln(50kPa/45kPa)] + [ –2°C – (–6°C)] · ln(55kPa/50kPa)] }
CAPE = [287 J·(K·kg)–1] · { 10K · 0.182 + 9.2K · 0.154 + 10K · 0.134 + 8K · 0.118 + 6K · 0.105 + 4K · 0.095 }
CAPE = [287 J·(K·kg)–1] · 6.53 K = 1874 J·kg–1.
Check: Physics and units OK.
Exposition: Theoretically, we should get exactly the same answer as we found in the previous Sample Application. Considering the coarseness of the boxes that I used in both Sample Applications, I am happy that the answers are as close as they are. I found the heighttiling method easier than the pressure-tiling method.
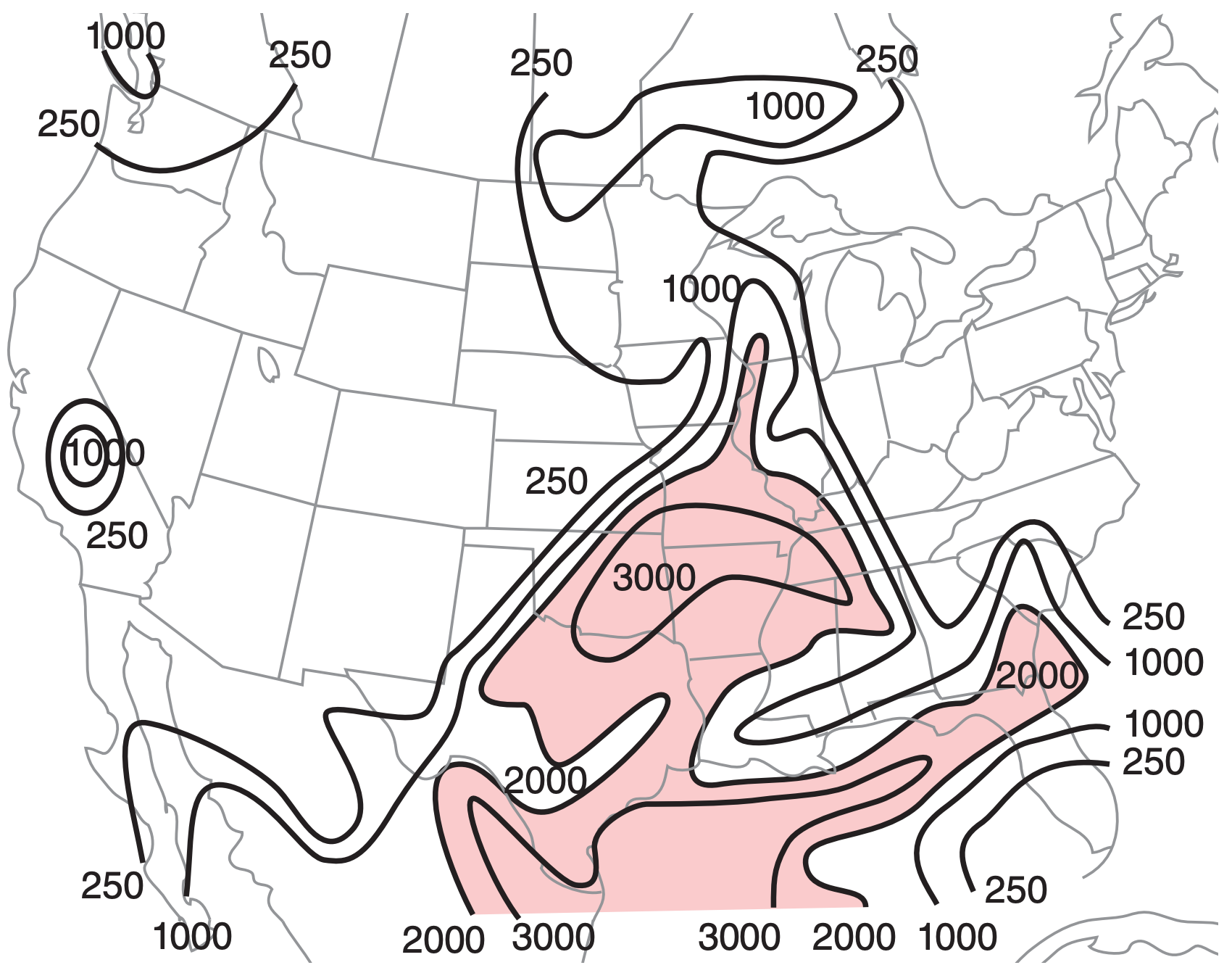
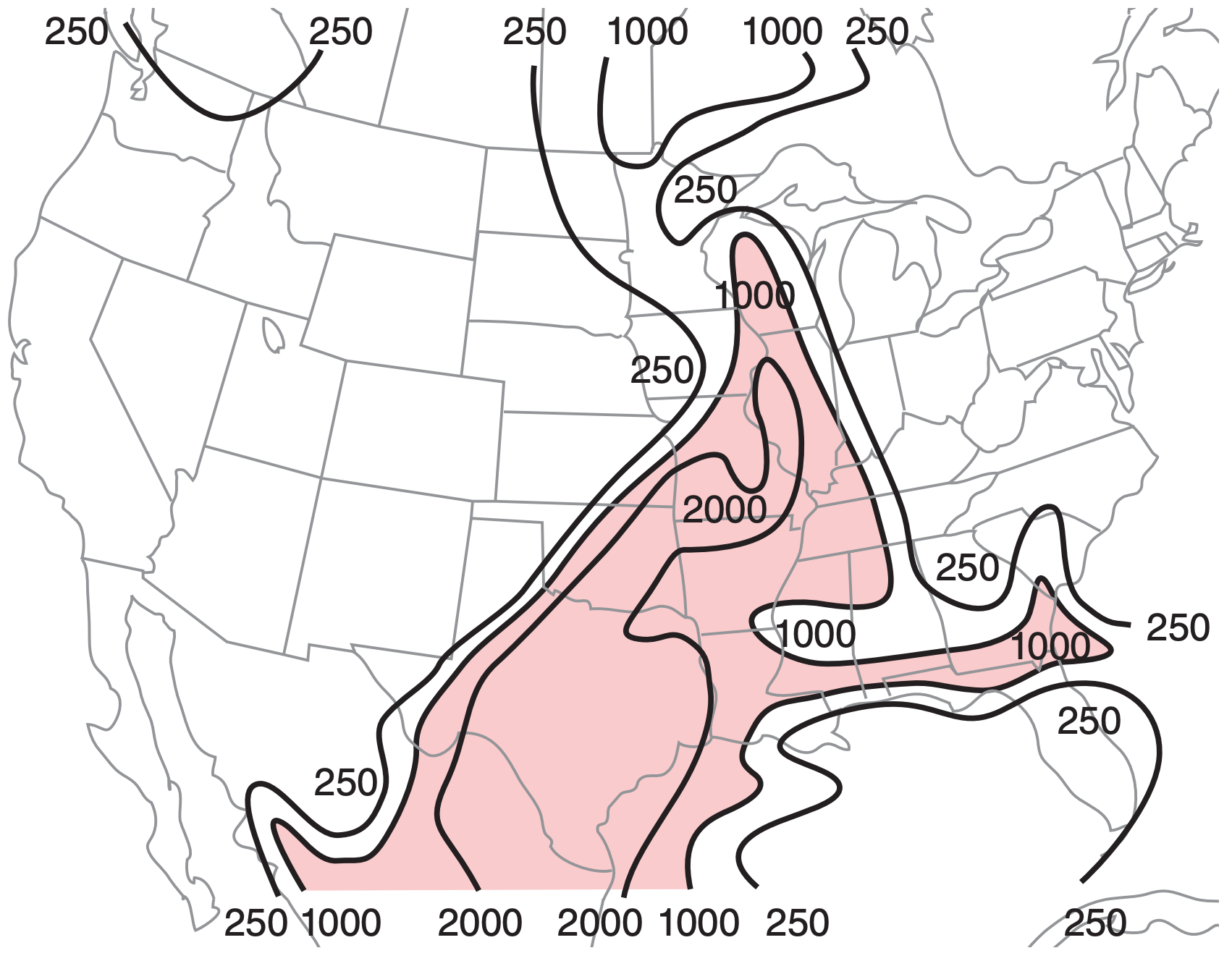
CAPE values vary greatly with location and time. By finding the CAPE for many locations in a region (by using rawinsonde observations, or by using forecast soundings from numerical weather prediction models), you can write the CAPE values on a weather map and then draw isopleths connecting lines of equal CAPE, such as shown in Fig. 14.38.
Other parcel-origin assumptions work better in other situations. If the pre-storm sounding is from earlier in the morning, then the forecast max surface temperature for that afternoon (along with the dew point forecast for that time) is a better choice for the rising air-parcel initial conditions (Fig. 14.39). This is also a type of SBCAPE.

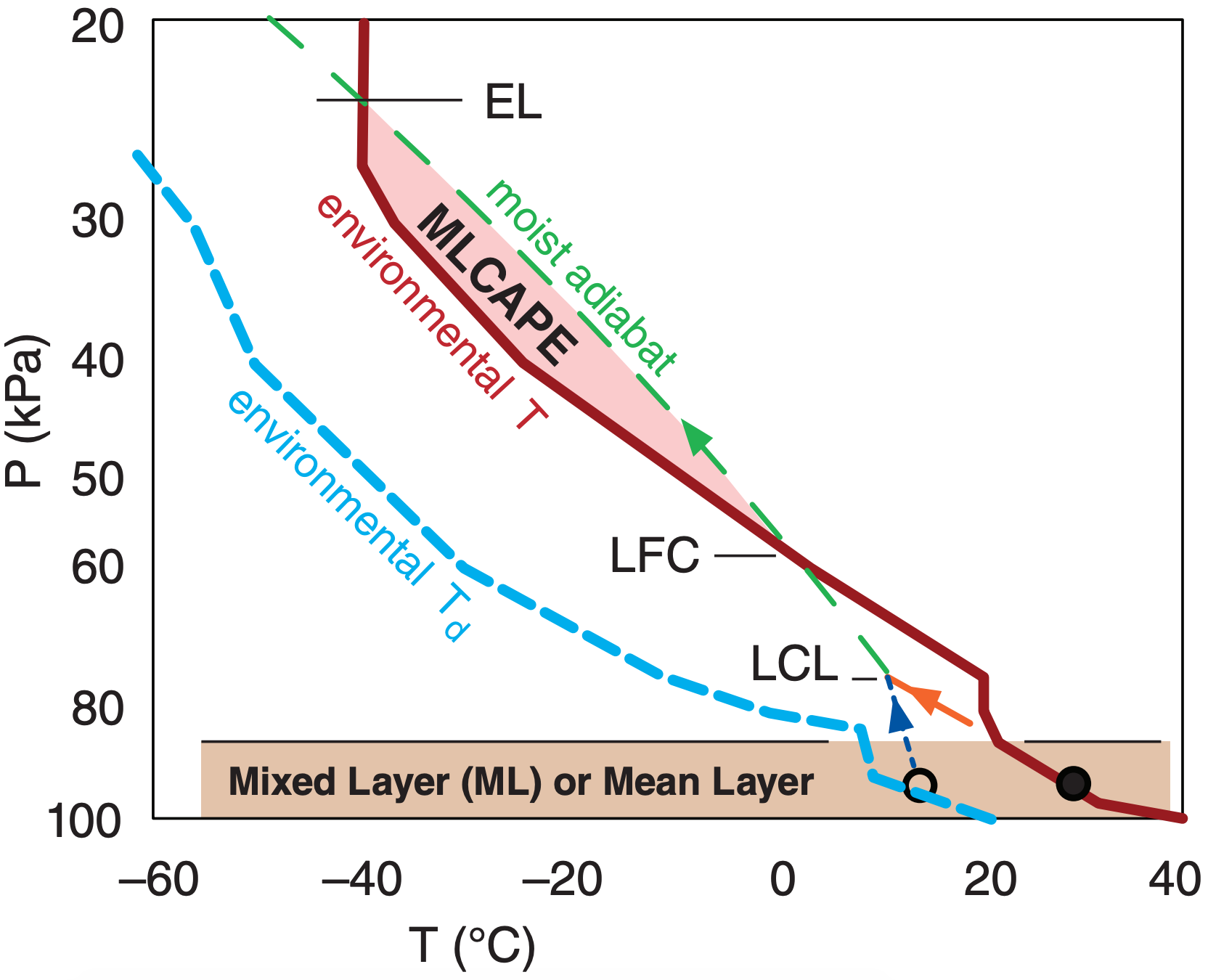
Another way is to average the conditions in the bottom 1 km (roughly 10 kPa) of the environmental sounding to better estimate ABL conditions. Thus, the initial conditions for the rising air parcel represent the mean layer (ML) conditions, or the mixed-layer (ML) conditions (Fig. 14.40). CAPE calculated this way is called Mean Layer CAPE (MLCAPE). Fig. 14.41 shows a case-study example of MLCAPE.
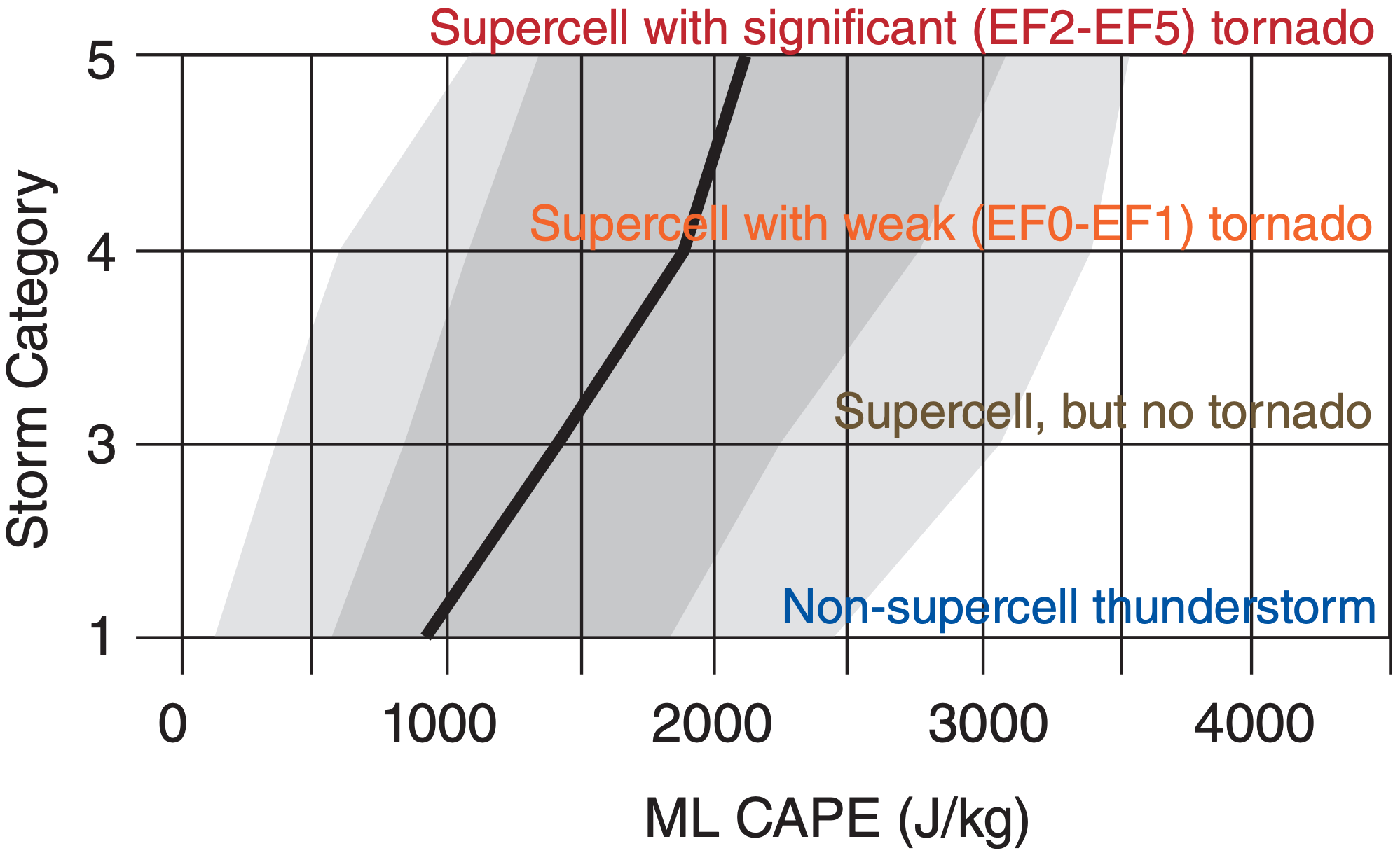
Early studies of thunderstorm occurrence vs. MLCAPE lead to forecast guidelines such as shown in Table 14-1. However, MLCAPE is not a sharp discriminator of thunderstorm intensity, as shown by the large overlap of storm categories in Fig. 14.42.
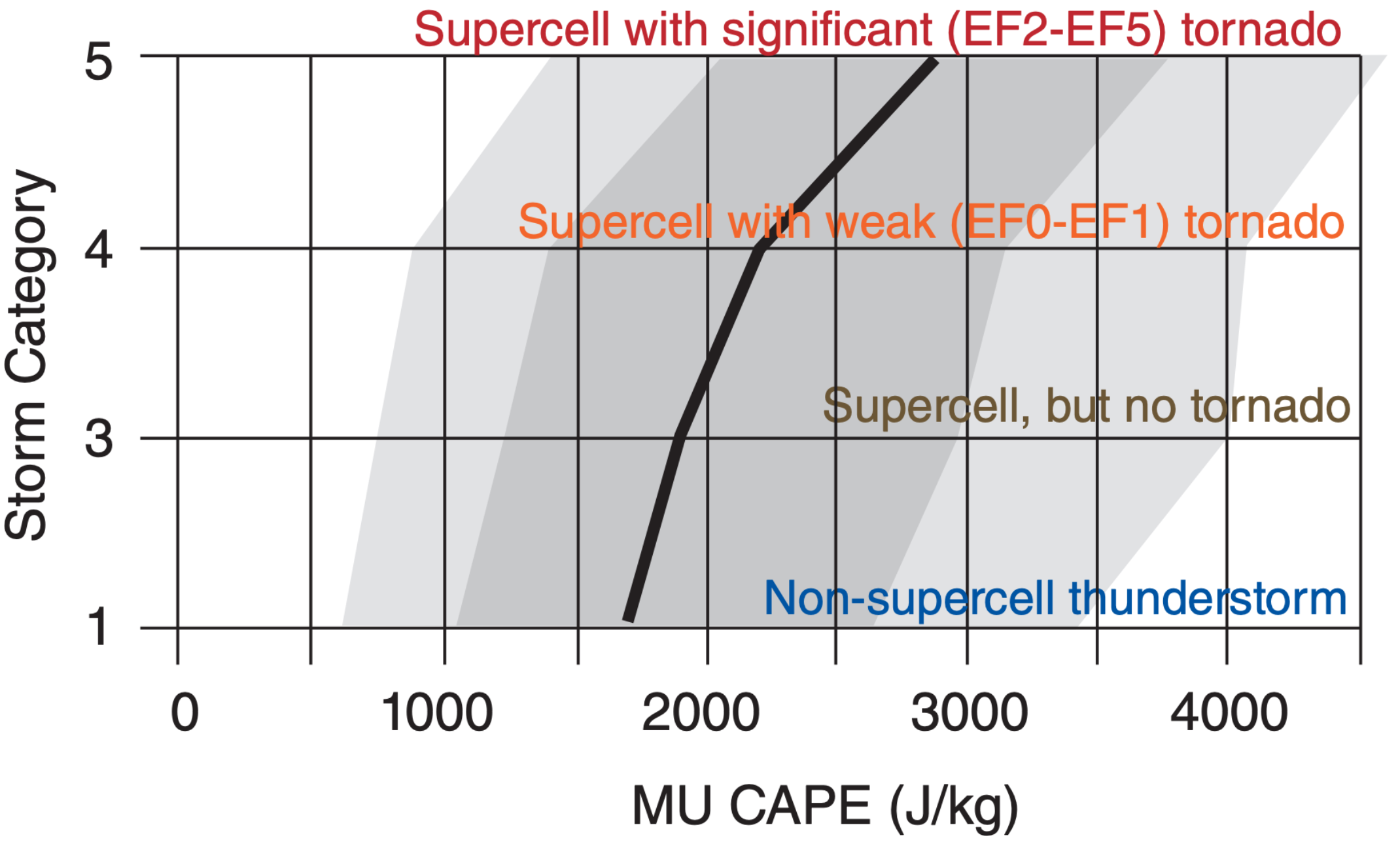
Yet another way is to calculate many different CAPEs for air parcels that start from every height in the bottom 30 kPa of the pre-storm environmental sounding, and then select the one that gives the greatest CAPE values. This is called the Most Unstable CAPE (MUCAPE). This method works even if thunderstorm updrafts are triggered by an elevated source, and also works for pre-storm soundings from any time of day. Although it is too tedious to compute these multiple CAPEs by hand, it is easily automated on a computer (Figs. 14.43 & 14.44). MUCAPE is always ≥ SBCAPE. But MUCAPE is not a sharp discriminator of thunderstorm intensity.

Sample Application
Assume a thunderstorm forms at the dot in Fig. 14.43, where MUCAPE ≈ 2700 J·kg–1. Estimate the possible intensity of this storm. Discuss the uncertainty.
Find the Answer
Given: MUCAPE ≈ 2,700 J·kg–1 at the dot (•) in Fig. 14.43, located in southern Illinois.
Find: Possible storm intensity. Discuss uncertainty
Use Fig. 14.44 to estimate intensity. For MUCAPE of 2,700 J·kg–1, the median line is about half way between “supercell with weak tornado (EF0-EF1)”, and “supercell with significant tornado (EF2-EF5).” So we might predict a supercell with an EF1 - EF2 tornado.
Exposition: Although there is some uncertainly in picking the MUCAPE value from Fig. 14.43, there is even greater uncertainty in Fig 14.44. Namely, within the interquartile range (dark shading) based on hundreds of past storms used to make this figure, there could easily be a supercell with no tornado, or a supercell with a significant tornado. There is even a chance of a non-supercell thunderstorm.
Thus, MUCAPE is not capable of sharply distinguishing thunderstorm intensity.
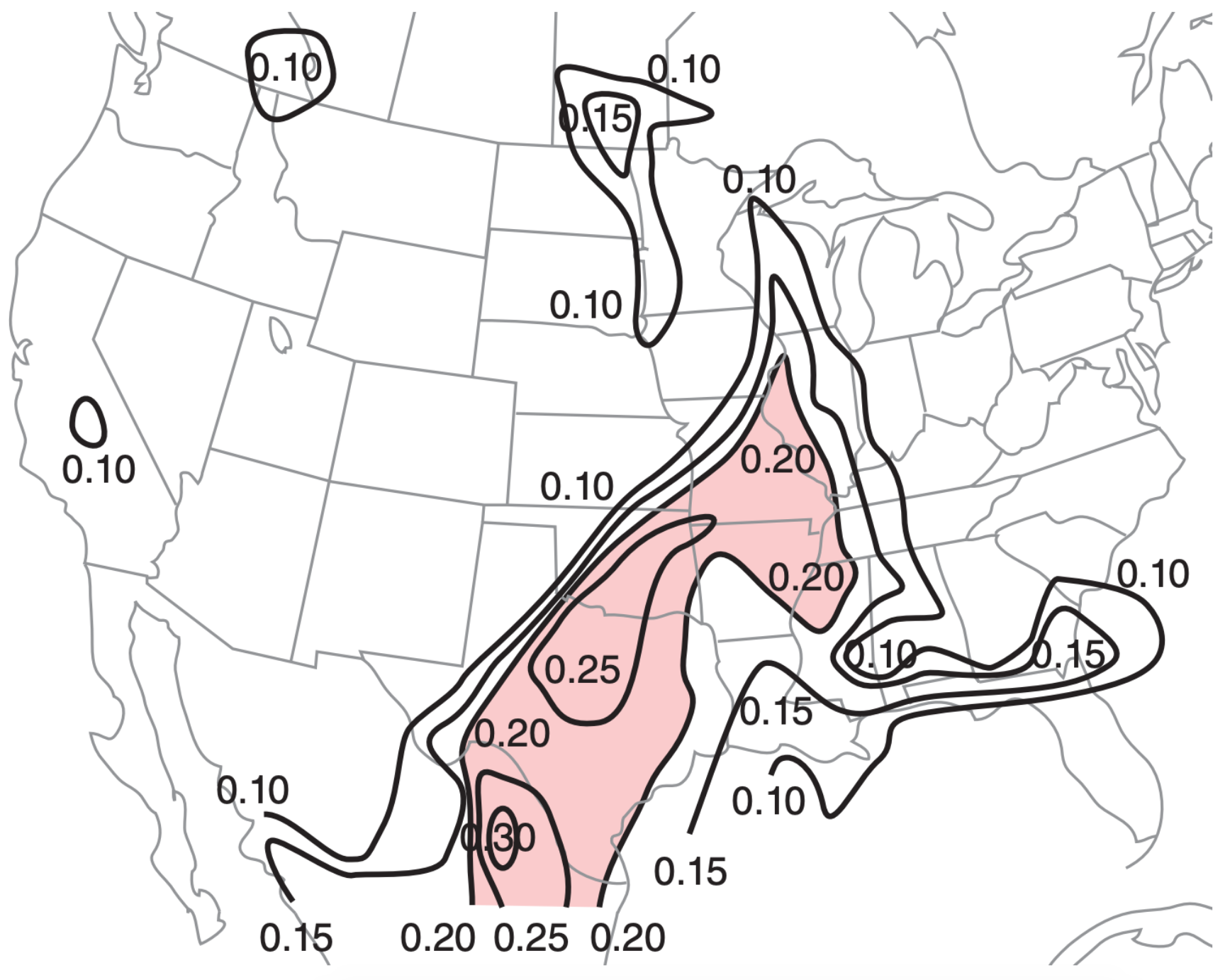
The shape of the CAPE area gives some information about the storm. To aid shape interpretation, a normalized CAPE (nCAPE) is defined as
\(\ \begin{align} n C A P E=\frac{C A P E}{z_{E L}-z_{L F C}}\tag{14.6}\end{align}\)
where zEL is height of the equilibrium level, zLFC is height of the level of free convection, and the units of nCAPE are m·s–2 or J·(kg·m)–1. Tall, thin CAPE areas (i.e., nCAPE ≤ 0.1 m·s–2) often suggest heavy precipitation, but unlikely tornadoes. Short, wide CAPE area (i.e., nCAPE ≥ 0.3 m·s–2) in the mid to lower part of the sounding can result in thunderstorms with strong, low-altitude updrafts, which cause vertical stretching of the air, intensification of rotation, and greater chance of tornadoes. See Fig. 14.45.
A word of caution: CAPE gives only an estimate of the strength of a thunderstorm if one indeed forms. It is a necessary condition, but not a sufficient condition. To form a thunderstorm, there must also be a process that triggers it. Often no thunderstorms form, even in locations having large CAPE. If thunderstorms are triggered, then larger CAPE indicates greater instability, stronger updrafts, and a chance for more violent thunderstorms. It is a useful but not perfect forecast tool, as demonstrated by the lack of statistical sharpness (Figs. 14.42, & 14.44).
14.4.2. Updraft Velocity
You can also use CAPE to estimate the updraft speed in thunderstorms. Recall from basic physics that kinetic energy per unit mass is KE/m = 0.5·w2, where w is updraft speed. Suppose that all the convective available potential energy could be converted into kinetic energy; namely, CAPE = KE/m. Combining the two equations above gives
\(\ \begin{align} w_{\max }=\sqrt{2 \cdot C A P E}\tag{14.7}\end{align}\)
which gives unrealistically large speed because it neglects entrainment of unsaturated air, frictional drag, and liquid-water loading. Studies of actual thunderstorm updrafts find that the most likely max updraft speed is
\(\ \begin{align} w_{\text {max likely }} \approx w_{\max } / 2\tag{14.8}\end{align}\)
Air in an updraft has inertia and can overshoot above the EL. Such penetrative convection can be seen by eye as mound or turret of cloud that temporarily overshoots above the top of the thunderstorm anvil. You can also see it in some satellite images. As stated before, such turrets or domes give a good clue to storm spotters that the thunderstorm is probably violent, and has strong updrafts. Such strong updrafts are felt as severe or extreme turbulence by aircraft.
Sample Application
For the sounding in Fig. 14.36 (CAPE = 1976 J·kg–1) find thunderstorm intensity, normalized CAPE, max updraft velocity, and likely updraft velocity.
Find the Answer
Given: Fig. 14.36, with CAPE = 1976 J·kg–1
Find: Intensity = ? , nCAPE = ? m·s–2, wmax & wmax likely = ? m s–1
a) From Table 14-1, moderate thunderstorms.
b) By eye using Fig. 14.36, the bottom and top of the CAPE region are zLFC ≈ 4.2 km, and zEL = 9.6 km. Use eq. (14.6): nCAPE=(1976 J·kg–1)/[9600–4200m]=0.37m·s–2.
c) Use eq. (14.7): wmax = [2 · (1976 m2 s–2) ]1/2 = wmax = 63 m s–1 .
d) Use eq (14.8): wmax likely = (63 m s–1)/2 = 31 m s–1 .
Check: Physics and units OK. Figure OK.
Exposition: Because the LFC is at such a high altitude, the CAPE area is somewhat short and fat, as indicated by the small value of nCAPE. Thus, strong low-altitude updrafts and tornadoes are possible. This thunderstorm has violent updrafts, which is why aircraft would avoid flying through it.


