11.6: Thermal Wind Effect
- Page ID
- 9601
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recall that horizontal temperature gradients cause vertically varying horizontal pressure gradients (Fig. 11.17), and that horizontal pressure gradients drive geostrophic winds. We can combine those concepts to see how horizontal temperature gradients drive vertically varying geostrophic winds. This is called the thermal wind effect.
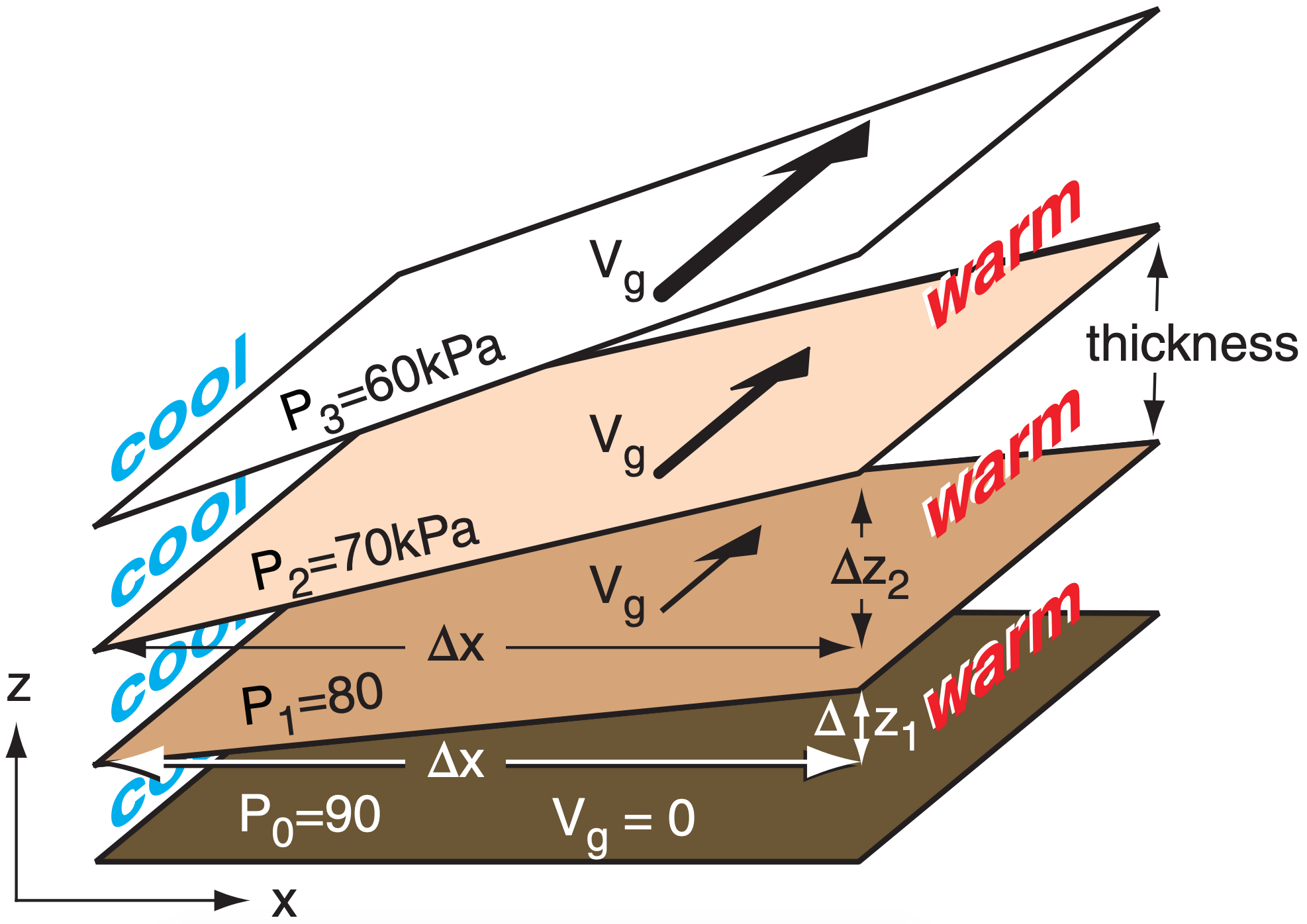
This effect can be pictured via the slopes of isobaric surfaces (Fig. 11.20). The hypsometric equation from Chapter 1 describes how there is greater thickness between any two isobaric (constant pressure) surfaces in warm air than in cold air. This causes the tilt of the isobaric surfaces to change with altitude. But as described by eq. (10.29), tilting isobaric surface imply a pressure-gradient force that can drive the geostrophic wind (Ug, Vg).
The relationship between the horizontal temperature gradient and the changing geostrophic wind with altitude is known as the thermal wind effect. After a bit of manipulation (see the Higher Math box on the next page), one finds that:
\(\ \begin{align} \frac{\Delta U_{g}}{\Delta z} \approx \frac{-|g|}{T_{v} \cdot f_{c}} \cdot \frac{\Delta T_{v}}{\Delta y}\tag{11.13a}\end{align}\)
\(\ \begin{align} \frac{\Delta V_{g}}{\Delta z} \approx \frac{|g|}{T_{v} \cdot f_{c}} \cdot \frac{\Delta T_{v}}{\Delta x}\tag{11.13b}\end{align}\)
where the Coriolis parameter is fc, virtual absolute temperature is Tv, and gravitational acceleration magnitude is |g| = 9.8 m·s–2. Thus, the meridional temperature gradient causes the zonal geostrophic winds to change with altitude, and the zonal temperature gradient causes the meridional geostrophic winds to change with altitude.
Above the atmospheric boundary layer, actual winds are nearly equal to geostrophic or gradient winds. Thus, eqs. (11.13) provide a first-order estimate of the variation of actual winds with altitude.
Sample Application
While driving north a distance of 500 km, your car thermometer shows the outside air temperature decreasing from 20°C to 10°C. How does the theoretical geostrophic wind change with altitude?
Find the Answer
Given: ∆y = 500 km, ∆T = 10°C – 20°C = –10°C, average T = 0.5·(10+20°C) = 15°C = 288 K.
Find: ∆Ug/∆z = ? (m s–1)/km
Given lack of other data, for simplicity assume: fc = 10–4 s–1, and Tv = T (i.e., air is dry).
Apply eq. (11.13a):
\(\frac{\Delta U_{g}}{\Delta z} \approx \frac{-\left(9.8 \mathrm{m} / \mathrm{s}^{2}\right)}{(288 \mathrm{K}) \cdot\left(10^{-4} \mathrm{s}^{-1}\right)} \cdot \frac{\left(-10^{\circ} \mathrm{C}\right)}{(500 \mathrm{km})}=6.81\left(\mathrm{m} \mathrm{s}^{-1}\right) / \mathrm{km}\)
Check: Physics & units reasonable. Agrees with Fig.
Exposition: Even if the wind were zero at the ground, the answer indicates that a west wind will increase in speed by 6.81 m s–1 for each 1 km of altitude gained.
Given no info about temperature change in the x direction, assume uniform temperature, which implies ∆Vg/∆z = 0 from eq. (11.13b). Namely, the south wind is constant with altitude.
11.6.1. Definition of Thickness
Problem: Derive Thermal Wind eq. (11.13a).
Find the Answer Start with the definitions of geostrophic wind (10.26a) and hydrostatic balance (1.25b):
\(U_{g}=-\frac{1}{\rho \cdot f_{c}} \frac{\partial P}{\partial y} \quad\) and \(\quad \rho \cdot|g|=-\frac{\partial P}{\partial z}\)
Replace the density in both eqs using the ideal gas law (1.20). Thus:
\(\frac{U_{g} \cdot f_{c}}{T_{v}}=-\frac{\Re_{d}}{P} \frac{\partial P}{\partial y}\) and \(\frac{|g|}{T_{v}}=-\frac{\Re_{d}}{P} \frac{\partial P}{\partial z}\)
Use (1/P)·∂P = ∂ln(P) from calculus to rewrite both:
\(\frac{U_{g} \cdot f_{c}}{T_{v}}=-\Re_{d} \frac{\partial \ln (P)}{\partial y} \quad\) and \(\quad \frac{|g|}{T_{v}}=-\Re_{d} \frac{\partial \ln (P)}{\partial z}\)
Differentiate the left eq. with respect to z:
\(\frac{\partial}{\partial z}\left(\frac{U_{g} \cdot f_{c}}{T_{v}}\right)=-\Re_{d} \frac{\partial \ln (P)}{\partial y \partial z}\)
and the right eq. with respect to y:
\(\frac{\partial}{\partial y}\left(\frac{|g|}{T_{v}}\right)=-\Re_{d} \frac{\partial \ln (P)}{\partial y \partial z}\)
But the right side of both eqs are identical, thus we can equate the left sides to each other:
\(\frac{\partial}{\partial z}\left(\frac{U_{g} \cdot f_{c}}{T_{v}}\right)=\frac{\partial}{\partial y}\left(\frac{|g|}{T_{v}}\right)\)
Next, do the indicated differentiations, and rearrange to get the exact relationship for thermal wind:
\(\frac{\partial U_{g}}{\partial z}=-\frac{|g|}{T_{v} \cdot f_{c}} \frac{\partial T_{v}}{\partial y}+\frac{U_{g}}{T_{v}}\left(\frac{\partial T_{v}}{\partial z}\right)\)
The last term depends on the geostrophic wind speed and the lapse rate, and has magnitude of 0 to 30% of the first term on the right. If we neglect the last term, we get the approximate thermal wind relationship:
\(\ \begin{align} \frac{\partial U_{g}}{\partial z} \approx-\frac{|g|}{T_{v} \cdot f_{c}} \frac{\partial T_{v}}{\partial y}\tag{11.13a}\end{align}\)
Exposition: A barotropic atmosphere is when the geostrophic wind does not vary with height. Using the exact equation above, we see that this is possible only when the two terms on the right balance.

In Fig. 11.20, focus on two isobaric surfaces, such as P = 90 kPa (dark brown in that figure), and P = 80 kPa (medium brown). These two surfaces are at different altitudes z, and the altitude difference is called the “thickness”. For our example, we focused on the “90 to 80 kPa thickness”. For any two isobaric surfaces P1 and P2 having altitudes zP1 and zP2 , the thickness is defined as
\(\ \begin{align} T H=z_{P 2}-z_{P 1}\tag{11.14}\end{align}\)
The hypsometric equation from Chapter 1 tells us that the thickness is proportional to the average absolute virtual-temperature within that layer. Colder air has thinner thickness. Thus, horizontal changes in temperature must cause horizontal changes in thickness.
Weather maps of “100 to 50 kPa thickness” such as Fig. 11.21 are often created by forecast centers. Larger thickness on this map indicates warmer air within the lowest 5 km of the atmosphere.
11.6.2. Thermal-wind Components
Suppose that we use thickness TH as a surrogate for absolute virtual temperature. Then we can combine eqs. (11.14) and (10.29) to yield:
\(\ \begin{align} u_{T H}=U_{G 2}-U_{G 1}=-\frac{|g|}{f_{c}} \frac{\Delta T H}{\Delta y}\tag{11.15a}\end{align}\)
\(\ \begin{align} V_{T H}=V_{G 2}-V_{G 1}=+\frac{|g|}{f_{c}} \frac{\Delta T H}{\Delta x}\tag{11.15b}\end{align}\)
where UTH and VTH are components of the thermal wind, |g| = magnitude of gravitational-acceleration, fc = Coriolis parameter, (UG1, VG1) are geostrophic-wind components on the P1 isobaric surface, and (UG2, VG2) are geostrophic-wind components on the P2 isobaric surface.

The horizontal vector defined by (UTH, VTH) is the difference between the geostrophic wind vector on the P2 surface and the geostrophic wind vector on the P1 surface, as Fig. 11.22 demonstrates. The corresponding magnitude of the thermal wind MTH is:
\(\ \begin{align} M_{T H}=\sqrt{U_{T H}^{2}+V_{T H}^{2}}\tag{11.16}\end{align}\)
To illustrate this, consider two isobaric surfaces P2 = 50 kPa (shaded blue in Figure 11.22) and P1 = 100 kPa (shaded red). The P1 surface has higher height to the east (toward the back of this sketch). If you conceptually roll a ball bearing down this red surface to find the direction of the pressure gradient, and then recall that the geostrophic wind in the N. Hemisphere is 90° to the right of that direction, then you would anticipate a geostrophic wind G1 direction as shown by the red arrow. Namely, it is parallel to a constant height contour (dotted red line) pointing in a direction such that low heights are to the vector’s left.
Suppose cold air in the north (left side of this sketch) causes a small thickness of only 4 km between the red and blue surfaces. Warm air to the south causes a larger thickness of 5 km between the two isobaric surfaces. Adding those thicknesses to the heights of the P1 surface (red) give the heights of the P2 surface (blue). The blue P2 surface tilts more steeply than the red P1 surface, hence the geostrophic wind G2 is faster (blue arrow) and is parallel to a constant height contour (blue dotted line).
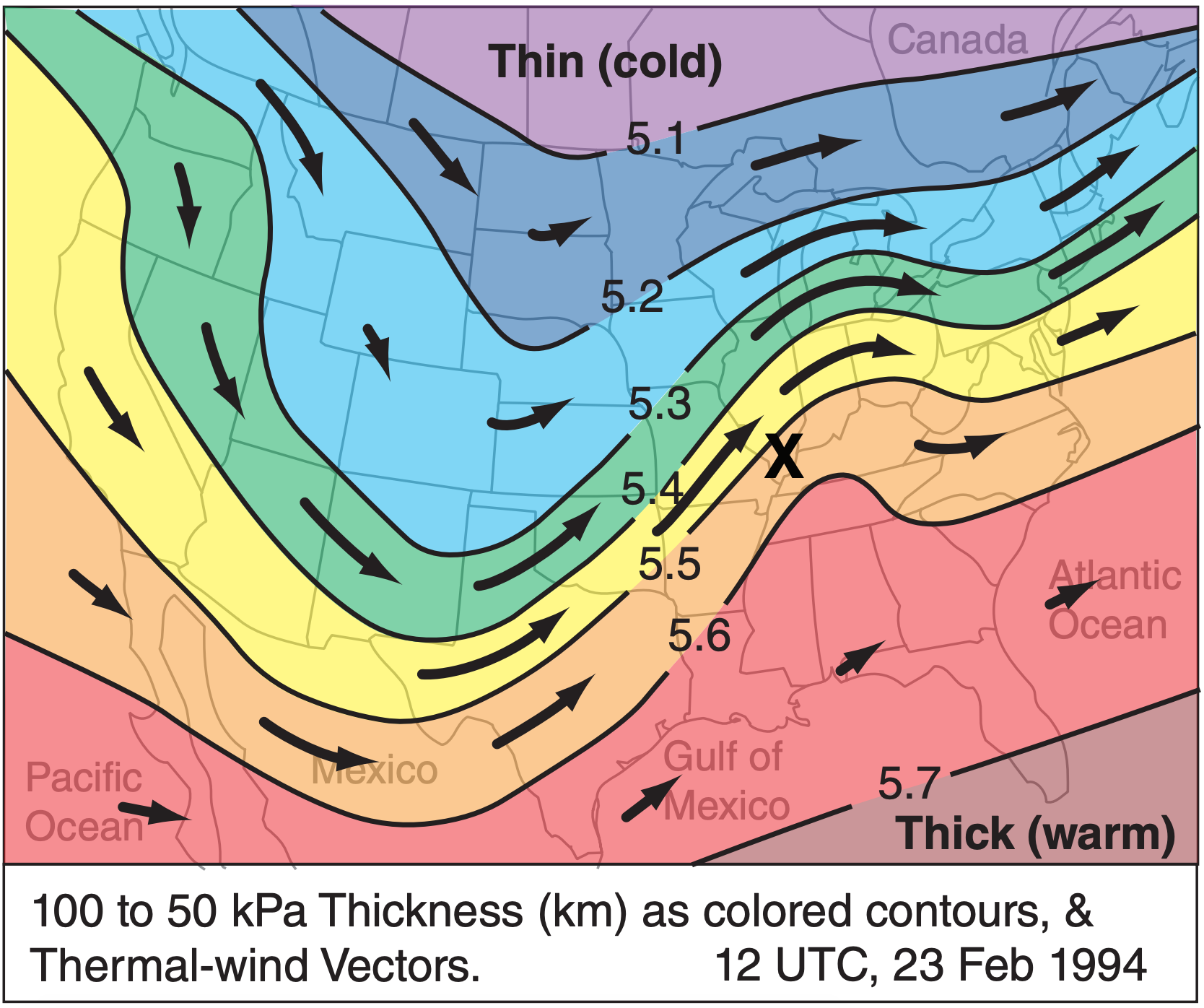
Projecting the G1 and G2 vectors to the ground (green in Fig. 11.22), the vector difference is shown in yellow, and is labeled as the thermal wind MTH. It is parallel to the contours of thickness (i.e., perpendicular to the temperature gradient between cold and warm air) pointing in a direction with cold air (thin thicknesses) to its left (Fig. 11.23).
Sample Application. For Fig. 11.22, what are the thermal-wind components. Assume fc = 1.1x10–4 s–1.
Find the Answer. Given: TH2 = 4 km, TH1 = 5 km, ∆y = 1000 km from the figure, fc = 1.1x10–4 s–1.
Find: UTH = ? m s–1, VTH = ? m s–1
Apply eq. (11.15a): \(U_{T H}=\frac{-|g|}{f_{c}} \frac{\Delta T H}{\Delta y}=\frac{-\left(9.8 \mathrm{ms}^{-2}\right) \cdot(4-5) \mathrm{km}}{\left(1.1 \times 10^{-4} \mathrm{s}^{-1}\right) \cdot(5000 \mathrm{km})}=17.8 \mathrm{m} \mathrm{s}^{-1}\)
Check: Physics & units are reasonable. Positive sign for UTH indicates wind toward positive x direction, as in Fig.
Exposition: With no east-to-west temperature gradient, and hence no east-to-west thickness gradient, we would expect zero north-south thermal wind;, hence, VTH = 0.
Thermal-wind magnitude is stronger where the thickness gradient is greater. Thus, regions on a weather map (Fig. 11.23) where thickness contours are closer together (i.e., have tighter packing) indicates faster thermal winds. The relationship between thermal winds and thickness contours is analogous to the relationship between geostrophic winds and height contours. But never forget that no physically realistic wind can equal the thermal wind, because the thermal wind represents the difference or shear between two geostrophic winds.
Nonetheless, you will find the thermal-wind concept useful because it helps you anticipate how geostrophic wind will change with altitude. Actual winds tend towards being geostrophic above the atmospheric boundary layer, hence the thermal-wind concept allows you to anticipate real wind shears.
11.6.3. Case Study
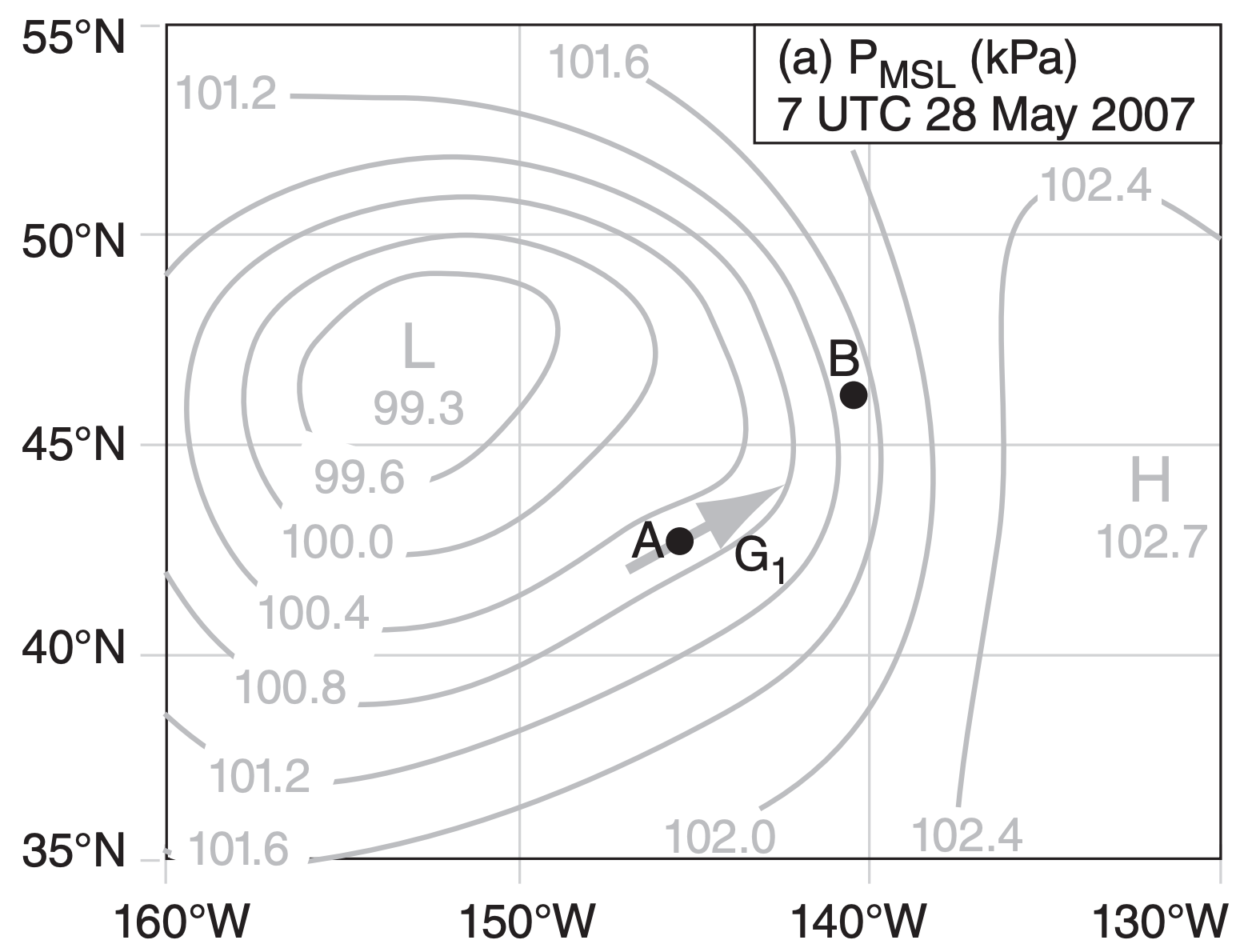
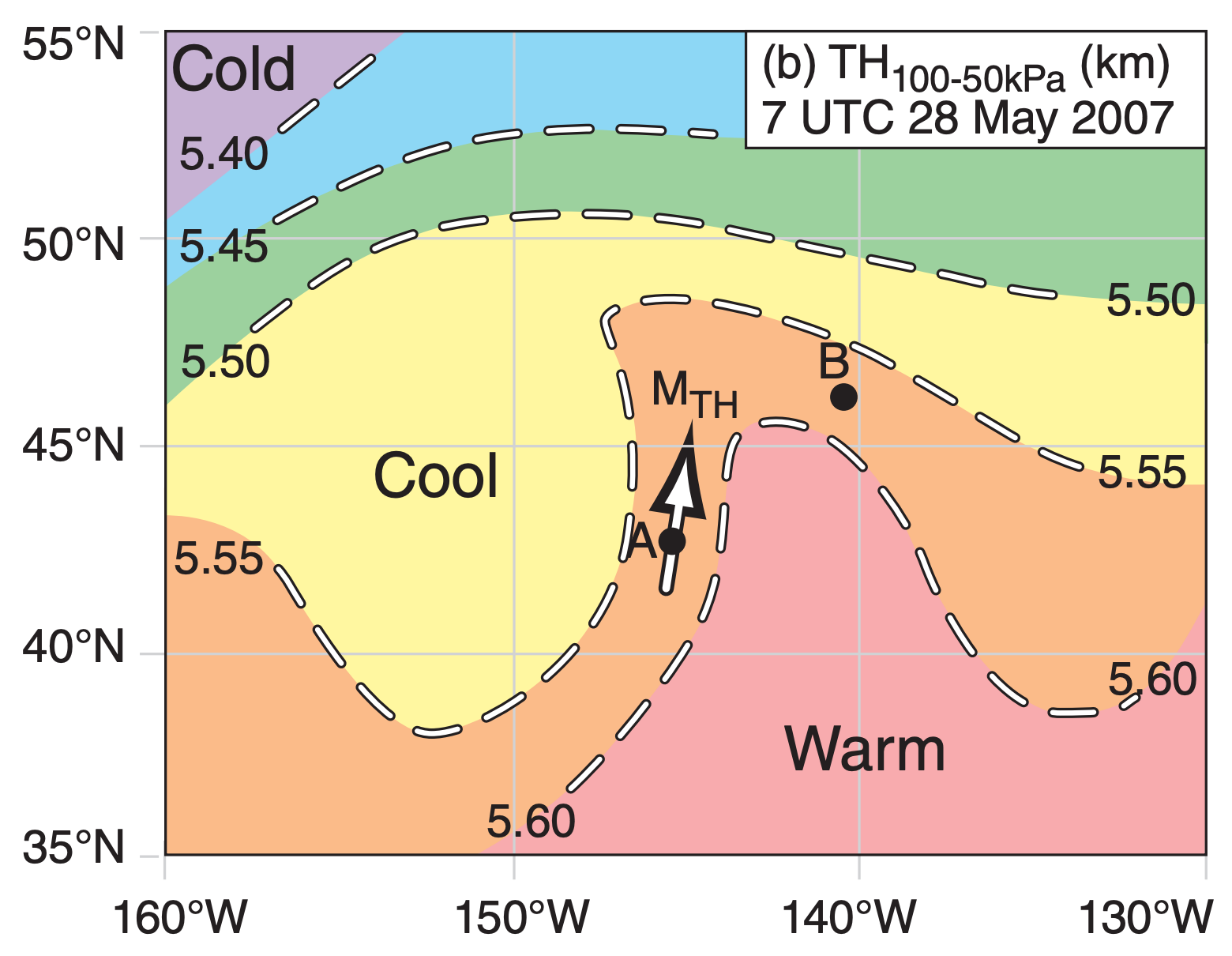
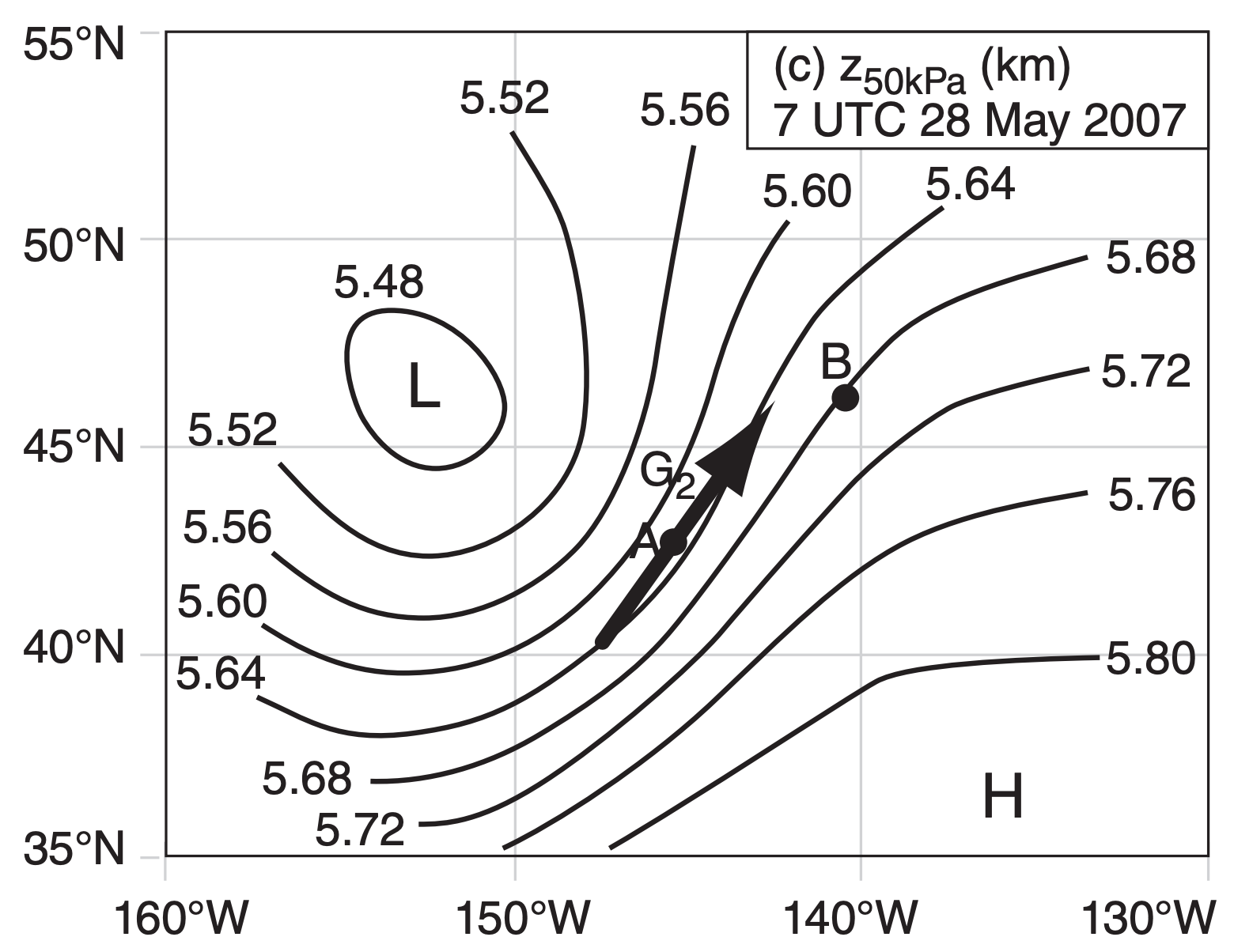
Figs. 11.24 show how geostrophic winds and thermal winds can be found on weather maps, and how to interpret the results. These maps may be copied onto transparencies and overlain.
Fig. 11.24a is a weather map of pressure at sea level in the N. Hemisphere, at a location over the northeast Pacific Ocean. As usual, L and H indicate low- and high-pressure centers. At point A, we can qualitatively draw an arrow (grey) showing the theoretical geostrophic (G1) wind direction; namely, it is parallel to the isobars with low pressure to its left.
Recall that pressures on a constant height surface (such as at height z = 0 at sea level) are closely related to geopotential heights on a constant pressure surface. So we can be confident that a map of 100 kPa heights would look very similar to Fig. 11.24a.
Fig. 11.24b shows the 100 - 50 kPa thickness map, valid at the same time and place. The thickness between the 100 and the 50 kPa isobaric surfaces is about 5.6 km in the warm air, and only 5.4 km in the cold air. The white arrow qualitatively shows the thermal wind MTH, as being parallel to the thickness lines with cold temperatures to its left.
Fig. 11.24c is a weather map of geopotential heights of the 50 kPa isobaric surface. L and H indicate low and high heights. The black arrow at A shows the geostrophic wind (G2), drawn parallel to the height contours with low heights to its left.
If we wished, we could have calculated quantitative values for G1, G2, and MTH, utilizing the scale that 5° of latitude equals 555 km. [ALERT: This scale does not apply to longitude, because the meridians get closer together as they approach the poles. However, once you have determined the scale (map mm : real km) based on latitude, you can use it to good approximation in any direction on the map.]
Back to the thermal wind: if you add the geostrophic vector from Fig. 11.24a with the thermal wind vector from Fig. 11.24b, the result should equal the geostrophic wind vector in Fig. 11.24c. This is shown in the Sample Application.
Although we will study much more about weather maps and fronts in the next few chapters, I will interpret these maps for you now.
Point A on the maps is near a cold front. From the thickness chart, we see cold air west and northwest of point A. Also, knowing that winds rotate counterclockwise around lows in the N. Hemisphere (see Fig. 11.24a), I can anticipate that the cool air will advance toward point A. Hence, this is a region of cold-air advection. Associated with this cold-air advection is backing of the wind (i.e., turning counterclockwise with increasing height), which we saw was fully explained by the thermal wind.
Point B is near a warm front. I inferred this from the weather maps because warmer air is south of point B (see the thickness chart) and that the counterclockwise winds around lows are causing this warm air to advance toward point B. Warm air advection is associated with veering of the wind (i.e., turning clockwise with increasing height), again as given by the thermal wind relationship. I will leave it to you to draw the vectors at point B to prove this to yourself.
Sample Application
For Fig. 11.24, qualitatively verify that when vector MTH is added to vector G1, the result is vector G2.
Find the Answer
Given: the arrows from Fig. 11.24 for point A.
These are copied and pasted here.
Find: The vector sum of G1 + MTH = ?
Recall that to do a vector sum, move the tail of the second vector (MTH) to be at the arrow head of the first vector (G1). The vector sum is then the vector drawn from the tail of the first vector to the tip (head) of the second vector.

Check: Sketch is reasonable.
Exposition: The vector sum indeed equals vector G2, as predicted by the thermal wind.
11.6.4. Thermal Wind & Geostrophic Adjustment - Part 2
Consider the red-shaded isobaric surface representing P = 60 kPa. That surface has high (H) heights to the south (to the right in this figure), and low (L) heights to the north. In the Northern Hemisphere, the geostrophic wind would be parallel to a constant height contour in a direction with lower pressure to its left. A similar interpretation can be made for the purpleshaded isobaric surface at P = 90 kPa. At a middle altitude in this sketch there is no net pressure gradient (i.e., zero slope of an isobaric surface), hence no geostrophic wind.
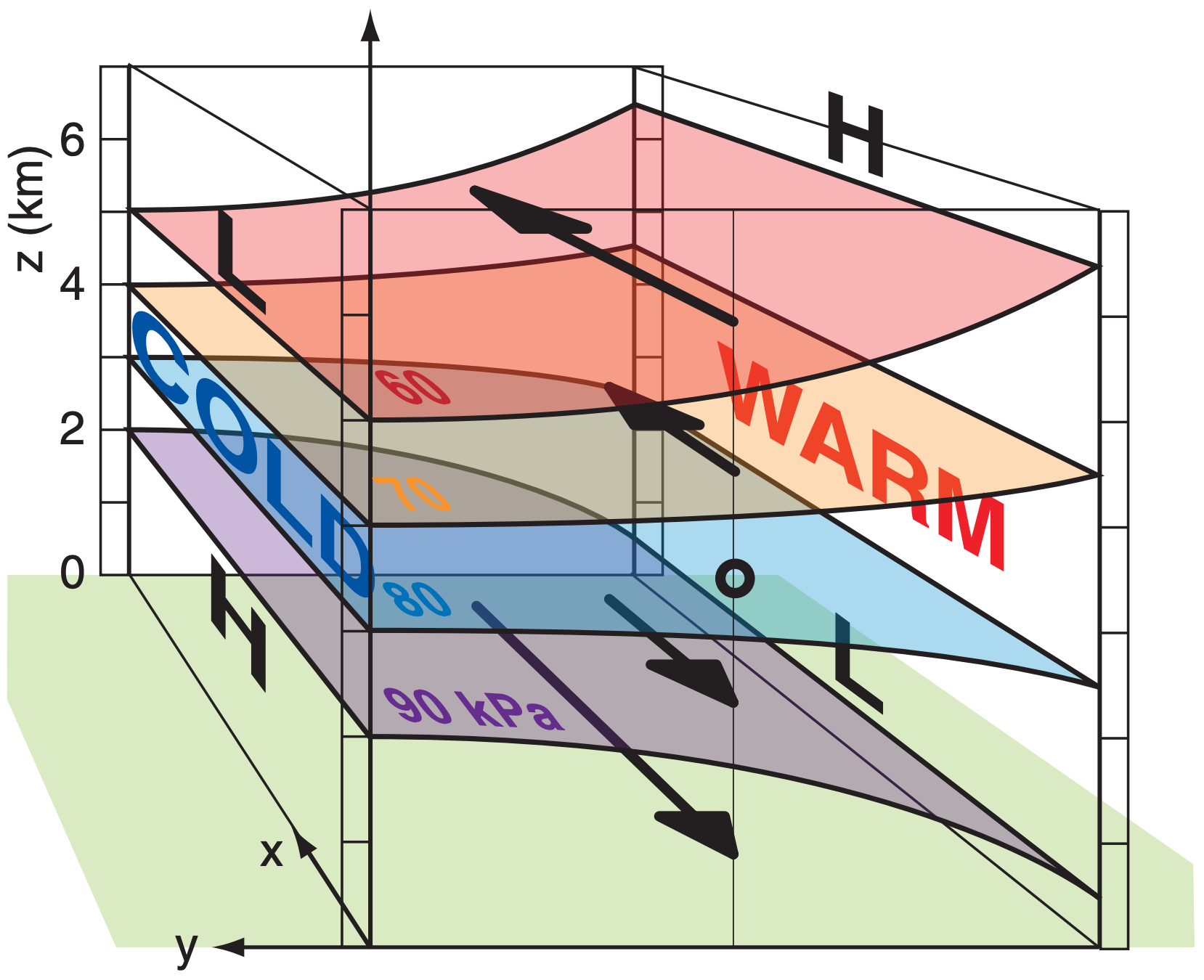
As geostrophic winds adjust to changes in pressure gradients, they move mass to alter the pressure gradients. Eventually, an equilibrium is approached (Fig. 11.25) based on the combined effects of geostrophic adjustment and the thermal wind. This figure is much more realistic than Fig. 11.17(iv) because Coriolis force prevents the winds from flowing directly from high to low pressure.
With these concepts of:
- differential heating,
- nonhydrostatic pressure couplets due to horizontal winds and vertical buoyancy,
- hydrostatic thermal circulations,
- geostrophic adjustment, and
- the thermal wind,
we can now go back and explain why the global circulation works the way it does.


