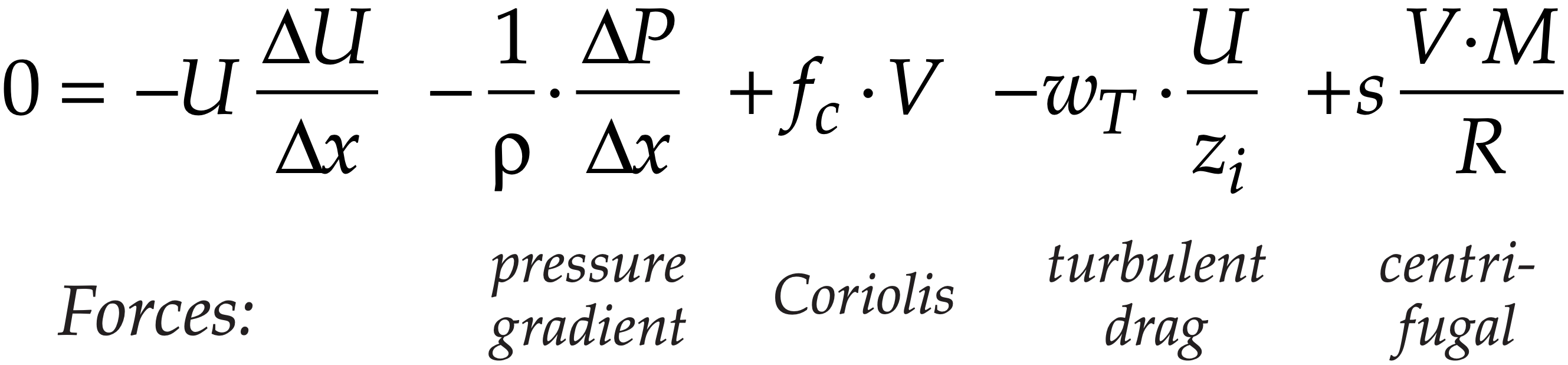10.5: Horizontal Winds

When air accelerates to create wind, forces that are a function of wind speed also change. As the winds continue to accelerate under the combined action of all the changing forces, feedbacks often occur to eventually reach a final wind where the forces balance. With a zero net force, there is zero acceleration.

Such a final, equilibrium, state is called steady state:

\(\ \begin{align} \dfrac{\Delta U}{\Delta t}=0, \quad \dfrac{\Delta V}{\Delta t}=0\tag{10.24}\end{align}\)

Caution: Steady state means no further change to the non-zero winds. Do not assume the winds are zero.

Under certain idealized conditions, some of the forces in the equations of motion are small enough to be neglected. For these situations, theoretical steady-state winds can be found based on only the remaining larger-magnitude forces. These theoretical winds are given special names, as listed in Table 10-4. These winds are examined next in more detail. As we discuss each theoretical wind, we will learn where we can expect these in the real atmosphere.

Table 10-4. Names of idealized steady-state horizontal winds, and the forces that govern them.
Wind Name
Geostrophic	•	•
Gradient	•	•		•
Atm.Bound. Layer	•	•	•
ABL Gradient	•	•	•	•
Cyclostrophic	•			•
Inertial		•		•
Antitriptic	•		•

10.5.1. Geostrophic Wind

Figure 10.8 Idealized weather map for the Northern Hemisphere, showing geostrophic wind (G, grey arrow) caused by a balance between two forces (brown arrows): pressure-gradient force (F_PG) and Coriolis force (F_CF). P is pressure, with isobars plotted as thin green lines. L and H are low and high-pressure regions. The small sphere represents an air parcel.

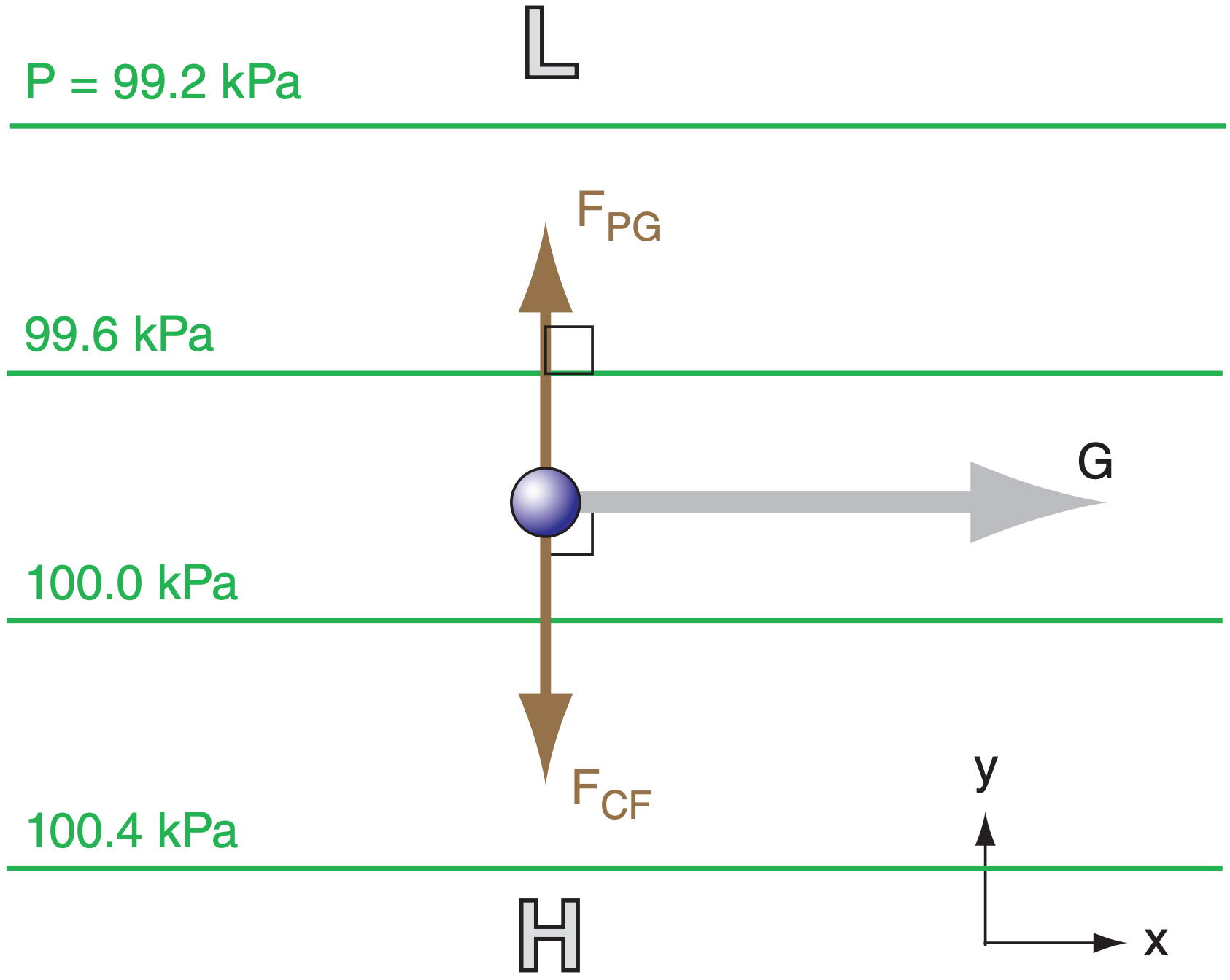
For special conditions where the only forces are Coriolis and pressure-gradient (Fig. 10.8), the resulting steady-state wind is called the geostrophic wind, with components (U_g , V_g). For this special case, the only terms remaining in, eqs. (10.23) are:

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta x}+f_{c} \cdot V\tag{10.25a}\end{align}\)

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta y}-f_{c} \cdot u\tag{10.25b}\end{align}\)

Define U ≡ U_g and V ≡ V_g in the equations above, and then solve for these wind components:

\(\ \begin{align} U_{g}=-\dfrac{1}{\rho \cdot f_{c}} \cdot \dfrac{\Delta P}{\Delta y}\tag{10.26a}\end{align}\)

\(\ \begin{align} V_{g}=+\dfrac{1}{\rho \cdot f_{c}} \cdot \dfrac{\Delta P}{\Delta x}\tag{10.26b}\end{align}\)

where f_c = (1.4584x10^–4 s^–1)·sin(latitude) is the Coriolis parameter, ρ is air density, and ∆P/∆x and ∆P/∆y are the horizontal pressure gradients.

Sample Application

Find geostrophic wind components at a location where ρ = 1.2 kg m^–3 and f_c = 1.1x10^–4 s^–1. Pressure decreases by 2 kPa for each 800 km of distance north.

Find the Answer

Given: f_c =1.1x10^–4 s^–1, ∆P= –2 kPa, ρ=1.2 kg m^–3, ∆y=800 km.

Find: (U_g , V_g) = ? m s^–1

But ∆P/∆x = 0 implies V_g = 0. For Ug, use eq. (10.26a):

\(U_{g}=\dfrac{-1}{\left(1.2 \mathrm{kg} / \mathrm{m}^{3}\right) \cdot\left(1.1 \times 10^{-4} s^{-1}\right)} \cdot \dfrac{(-2 \mathrm{kPa})}{(800 \mathrm{km})}=18.9 \mathrm{ms}^{-1}\)

Check: Physics & units OK. Agrees with Fig. 10.10.

Exposition: As the pressure gradient accelerates air northward, Coriolis force turns it toward the east.

Figure 10.9 Isobars (green lines) that are more closely spaced (i.e., tightly packed) cause stronger geostrophic winds (arrows), for N. Hemisphere

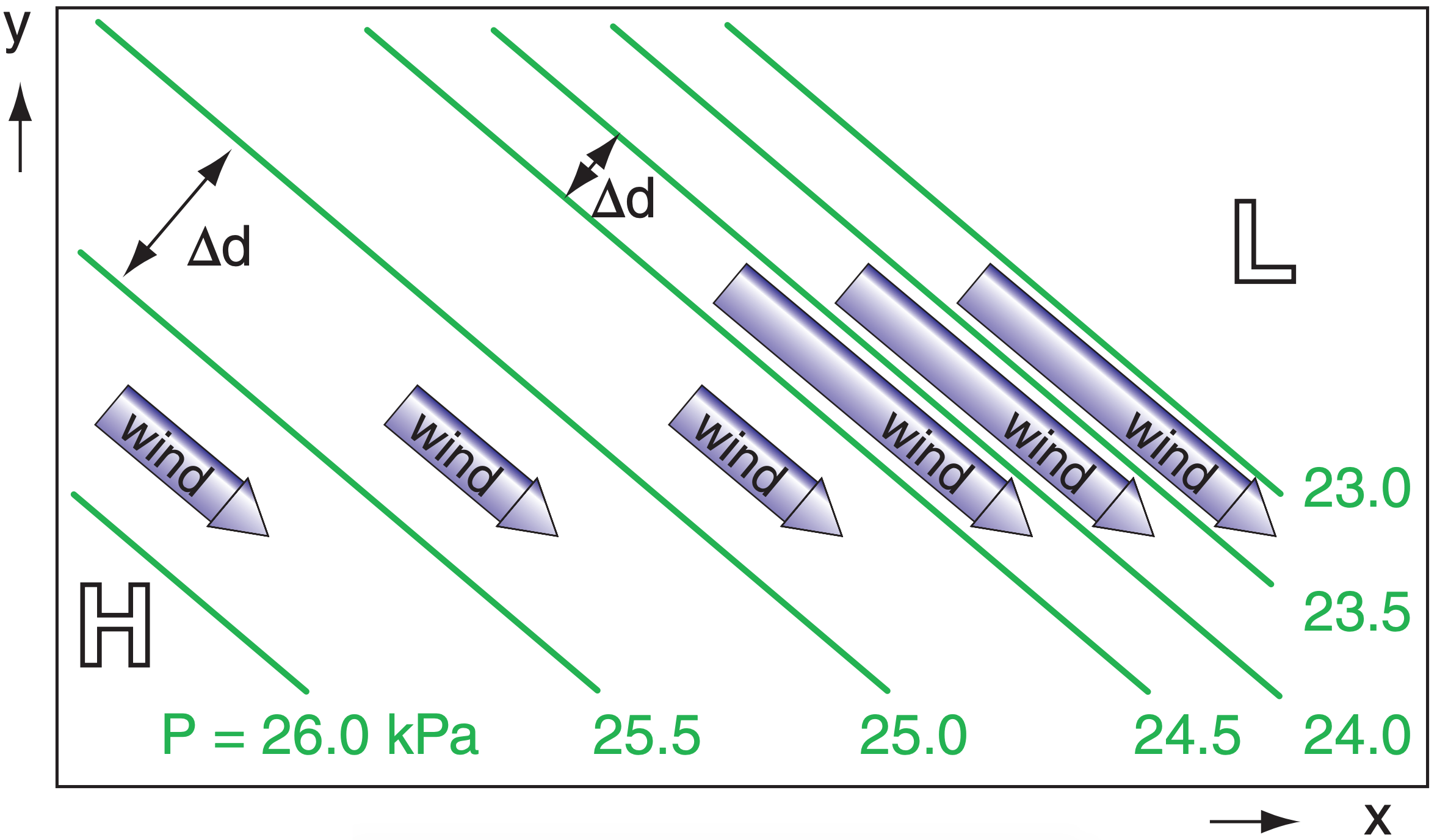
Real winds are nearly geostrophic at locations where isobars or height contours are relatively straight, for altitudes above the atmospheric boundary layer. Geostrophic winds are fast where isobars are packed closer together. The geostrophic wind direction is parallel to the height contours or isobars. In the N. (S.) hemisphere the wind direction is such that low pressure is to the wind’s left (right), see Fig. 10.9.

The magnitude G of the geostrophic wind is:

\(\ \begin{align} G=\sqrt{U_{g}^{2}+V_{g}^{2}}\tag{10.27}\end{align}\)

Figure 10.10 Variation of geostrophic wind speed (G) with horizontal pressure gradient (∆P/∆d) at sea level. Top scale is height gradient of any isobaric surface

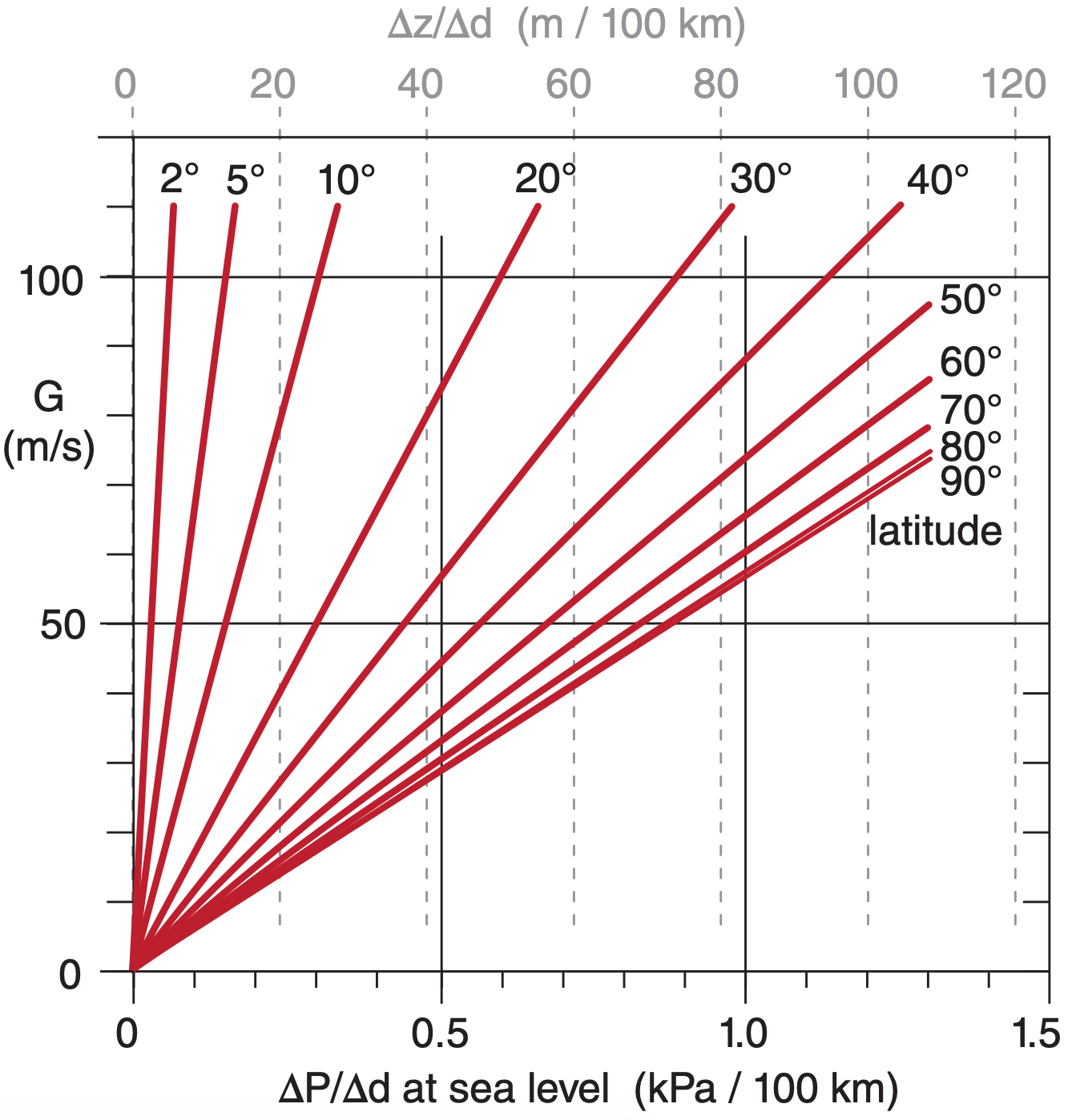
If ∆d is the distance between two isobars (in the direction of greatest pressure change; namely, perpendicular to the isobars), then the magnitude (Fig. 10.10) of the geostrophic wind is:

\(\ \begin{align} G=\left|\dfrac{1}{\rho \cdot f_{c}} \cdot \dfrac{\Delta P}{\Delta d}\right|\tag{10.28}\end{align}\)

Above sea level, weather maps are often on isobaric surfaces (constant pressure charts), from which the geostrophic wind (Fig. 10.10) can be found from the height gradient (change of height of the isobaric surface with horizontal distance):

\(\ \begin{align} U_{g}=-\dfrac{|g|}{f_{c}} \cdot \dfrac{\Delta z}{\Delta y}\tag{10.29a}\end{align}\)

\(\ \begin{align} V_{g}=+\dfrac{|g|}{f_{c}} \cdot \dfrac{\Delta z}{\Delta x}\tag{10.29b}\end{align}\)

where the Coriolis parameter is f_c , and gravitational acceleration is |g| = 9.8 m·s^–2. The corresponding magnitude of geostrophic wind on an isobaric chart is:

\(\ \begin{align} G=\left|\dfrac{g}{f_{c}} \cdot \dfrac{\Delta z}{\Delta d}\right|\tag{10.29c}\end{align}\)

Sample Application

Find the geostrophic wind for a height increase of 50 m per 200 km of distance toward the east. Assume, f_c = 0.9x10^–4 s^–1 .

Find the Answer

Given: ∆x = 200 km, ∆z = 50 m, f_c = 0.9x10^–4 s^–1 .

Find: G = ? m s^–1.

No north-south height gradient, thus U_g = 0.

Apply eq. (10.29b) and set G = V_g :

\(V_{g}=+\dfrac{|g|}{f_{c}} \cdot \dfrac{\Delta z}{\Delta x}=\left(\dfrac{9.8 \mathrm{ms}^{-2}}{0.00009 \mathrm{s}^{-1}}\right) \cdot\left(\dfrac{50 \mathrm{m}}{200,000 \mathrm{m}}\right)=27.2 \mathrm{ms}^{-1}\)

Check: Physics & units OK. Agrees with Fig. 10.10.

Exposition: If height increases towards the east, then you can imagine that a ball placed on such a surface would roll downhill toward the west, but would turn to its right (toward the north) due to Coriolis force.

INFO • Approach to Geostrophy

How does an air parcel, starting from rest, approach the final steady-state geostrophic wind speed G sketched in Fig. 10.8?

Start with the equations of horizontal motion (10.23), and ignore all terms except the tendency, pressuregradient force, and Coriolis force. Use the definition of geostrophic wind (eqs. 10.26) to write the resulting simplified equations as:

\(\Delta U / \Delta t=-f_{c} \cdot\left(V_{g}-V\right)\)
\(\Delta V / \Delta t=f_{c} \cdot\left(U_{g}-U\right)\)

Next, rewrite these as forecast equations:

\(U_{\text {new}}=U_{\text {old}}-\Delta t \cdot f_{c} \cdot\left(V_{g}-V_{\text {old}}\right)\)
\(V_{\text {new}}=V_{\text {old}}+\Delta t \cdot f_{c} \cdot\left(U_{g}-U_{\text {new}}\right)\)

Start with initial conditions (U_old, V_old) = (0, 0), and then iteratively solve the equations on a spreadsheet to forecast the wind.

For example, suppose ∆P = 1 kPa, f_c = 10^–4 s^–1, ∆x = 500 km, ρ = 1 kg m^–3, where we would anticipate the wind should approach (U_g, V_g) = (0, 20) m s^–1. The actual evolution of winds (U, V) and air parcel position (X, Y) are shown in Figs. below.

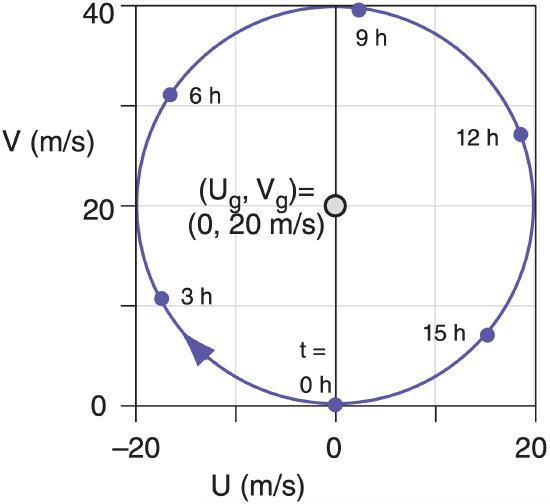
Surprisingly, the winds never reach geostrophic equilibrium, but instead rotate around the geostrophic wind. This is called an inertial oscillation, with period of 2·π/f_c. For our case, the period is 17.45 h.

Twice this period is called a pendulum day.

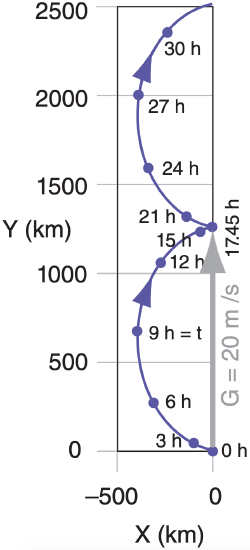The net result in the figure below is that the wind indeed moves at the geostrophic speed of 20 m s–1 to the north (≈ 1250 km in 17.45 h), but along the way it staggers west and east with an additional ageostrophic (non-geostrophic) part.

Inertial oscillations are sometimes observed at night in the atmospheric boundary layer, but rarely higher in the atmosphere. Why not? (1) The ageostrophic component of wind (wind from the East in this example) moves air mass, and changes the pressure gradient. (2) Friction damps the oscillation toward a steady wind.

If the geopotential Φ = |g|·z is substituted in eqs. (10.29), the resulting geostrophic winds are:

\(\ \begin{align} U_{g}=-\dfrac{1}{f_{c}} \cdot \dfrac{\Delta \Phi}{\Delta y}\tag{10.30a}\end{align}\)

\(\ \begin{align} V_{g}=\dfrac{1}{f_{c}} \cdot \dfrac{\Delta \Phi}{\Delta x}\tag{10.30b}\end{align}\)

10.5.2. Gradient Wind

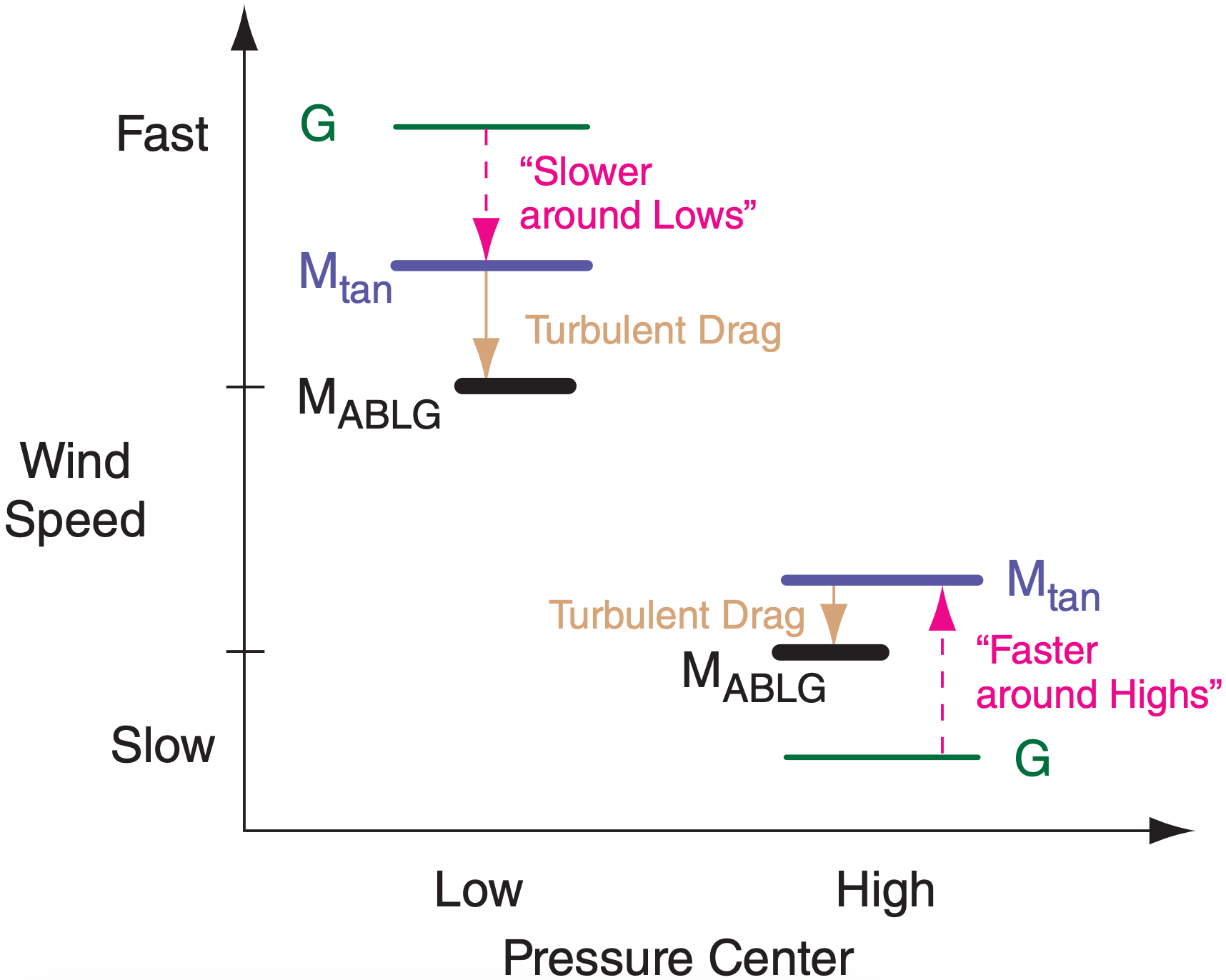
If there is no turbulent drag, then winds tend to blow parallel to isobar lines or height-contour lines even if those lines are curved. However, if the lines curve around a low-pressure center (in either hemisphere), then the wind speeds are subgeostrophic (i.e., slower than the theoretical geostrophic wind speed). For lines curving around high-pressure centers, wind speeds are supergeostrophic (faster than theoretical geostrophic winds). These theoretical winds following curved isobars or height contours are known as gradient winds.

Gradient winds differ from geostrophic winds because Coriolis force F_CF and pressure-gradient force F_PG do not balance, resulting in a non-zero net force F_net. This net force is called centripetal force, and is what causes the wind to continually change direction as it goes around a circle (Figs. 10.11 & 10.12). By describing this change in direction as causing an apparent force (centrifugal), we can find the equations that define a steady-state gradient wind:

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta x}+f_{c} \cdot V+s \cdot \dfrac{V \cdot M}{R} \tag{10.31a}\end{align}\)

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta y}-f_{c} \cdot U-s \cdot \dfrac{U \cdot M}{R}\tag{10.31b}\end{align}\)

Because the gradient wind is for flow around a circle, we can frame the governing equations in radial coordinates, such as for flow around a low:

\(\ \begin{align} \dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta R}=f_{C} \cdot M_{\tan }+\dfrac{M_{\tan }^{2}}{R}\tag{10.32}\end{align}\)

where R is radial distance from the center of the circle, f_c is the Coriolis parameter, ρ is air density, ∆P/∆R is the radial pressure gradient, and M_tan is the magnitude of the tangential velocity; namely, the gradient wind.

Figure 10.11 Forces (brown arrows) that cause the gradient wind (solid grey arrow, M_tan) to be slower than geostrophic (hollow grey arrow) when circling around a low-pressure center (called a cyclone in the N. Hem.). The short white arrow with black outline shows centripetal force (the imbalance between the other two forces). Centripetal force pulls the air parcel (blue sphere) inward to force the wind direction to change as needed for the wind to turn along a circular path.

Figure 10.12 Forces (brown arrows) that cause the gradient wind (solid grey arrow, M_tan) to be faster than geostrophic (hollow grey arrow) for an air parcel (blue sphere) circling around a high-pressure center (called an anticyclone in the N. Hemisphere).

Figure 10.13 Comparison of gradient winds M_tan vs. geostrophic wind G for flows around low (L) and high (H) pressures. N. Hemisphere.

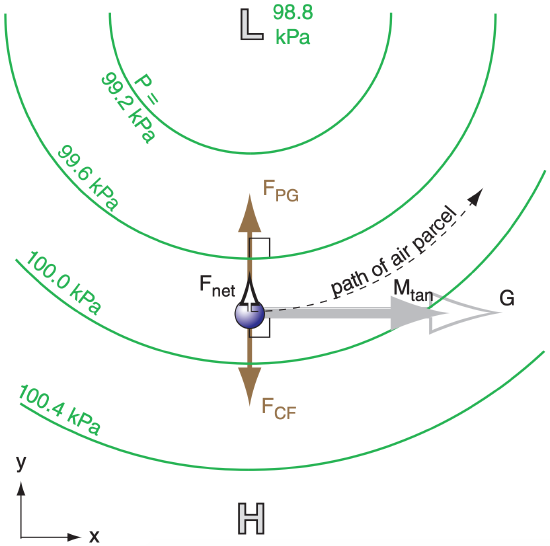
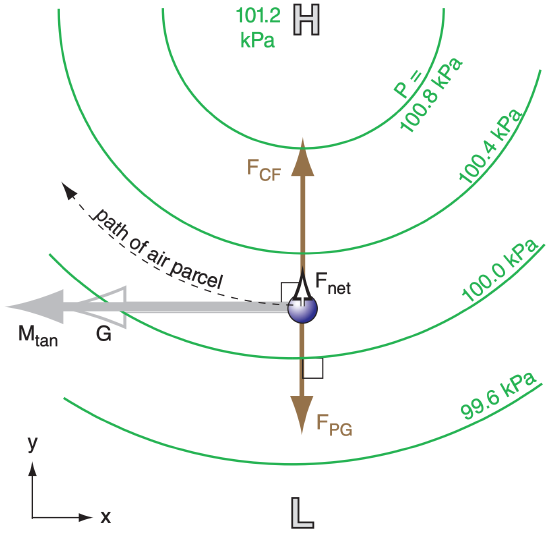
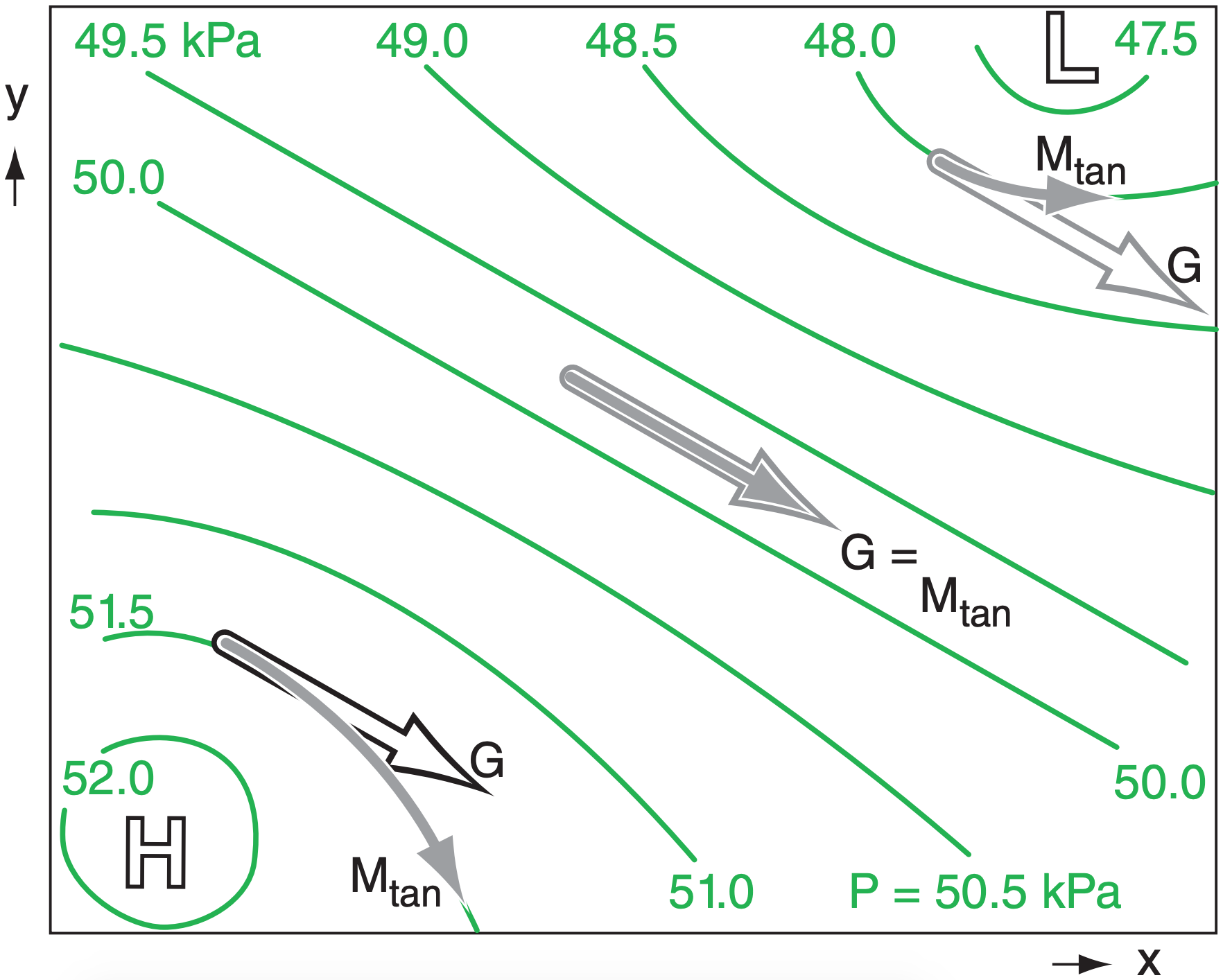
By re-arranging eq. (10.32) and plugging in the definition for geostrophic wind speed G, you can get an implicit solution for the gradient wind M_tan:

\(\ \begin{align} M_{\mathrm{tan}}=G \pm \dfrac{M_{\tan }^{2}}{f_{c} \cdot R}\tag{10.33}\end{align}\)

In this equation, use the + sign for flow around highpressure centers, and the – sign for flow around lows (Fig. 10.13).

Sample Application

What radius of curvature causes the gradient wind to equal the geostrophic wind?

Find the Answer

Given: M_tan = G

Find: R = ? km

Use eq. (10.33), with M_tan = G:

G = G ± G²/( f_c·R)

This is a valid equality G = G only when the last term in eq. (10.33) approaches zero; i.e., in the limit of R = ∞ .

Check: Eq. (10.33) still balances in this limit.

Exposition: Infinite radius of curvature is a straight line, which (in the absence of any other forces such as turbulent drag) is the condition for geostrophic wind.

INFO • The Rossby Number

The Rossby number (R_o) is a dimensionless ratio defined by

\(R o=\dfrac{M}{f_{c} \cdot L} \quad\) or \(\quad R o=\dfrac{M}{f_{c} \cdot R}\)

where M is wind speed, f_c is the Coriolis parameter, L is a characteristic length scale, and R is radius of curvature.

In the equations of motion, suppose that advection terms such as U·∆U/∆x are order of magnitude M²/L, and Coriolis terms are of order f_c·M. Then the Rossby number is like the ratio of advection to Coriolis terms: (M²/L) / (f_c·M) = M/(f_c·L) = Ro. Or, we could consider the Rossby number as the ratio of centrifugal (order of M²/R) to Coriolis terms, yielding M/(f_c·R) = Ro.

Use the Rossby number as follows. If Ro < 1, then Coriolis force is a dominant force, and the flow tends to become geostrophic (or gradient, for curved flow). If Ro > 1, then the flow tends not to be geostrophic.

For example, a midlatitude cyclone (low-pressure system) has approximately M = 10 m s^–1, f_c = 10^–4 s^–1, and R = 1000 km, which gives Ro = 0.1 . Hence, midlatitude cyclones tend to adjust toward geostrophic balance, because Ro < 1. In contrast, a tornado has roughly M = 50 m s^–1, f_c = 10^–4 s^–1, and R = 50 m, which gives Ro = 10,000, which is so much greater than one that geostrophic balance is not relevant.

Figure 10.14 Illustration of how mean sea-level pressure P can vary with distance R from a high-pressure (H) center. The anticyclone (i.e., the high) has zero horizontal pressure gradient and calm winds in its center, with weak pressure gradient (∆P/∆R) and gentle winds in a broad region around it. The cyclone (i.e., the low) can have steep pressure gradients and associated strong winds close to the low center (L), with a pressure cusp right at the low center. In reality (dotted line), turbulent mixing near the low center smooths the cusp, allowing a small region of light winds at the low center surrounded by stronger winds. Although this graph was constructed using eq. (10.37b), it approximates the pressure variation along the cross section shown in the next figure.

Figure 10.15 Illustration of strong pressure gradients (closely-spaced isobars) around the low-pressure center (L) over eastern Canada, and weak pressure gradients (isobars spaced further apart) around the high (H) over the NE Atlantic Ocean. NCEP reanalysis of daily-average mean sea-level pressure (Pa) for 5 Feb 2013. Pressures in the low & high centers were 96.11 & 104.05 kPa. Pressure variation along the dotted line is similar to that plotted in the previous figure. [Courtesy of the NOAA/NCEP Earth Systems Research Laboratory. http://www.esrl.noaa.gov/psd/ data/gridded/data.ncep.reanalysis.html ]

Figure 10.16 Relative wind speeds around low- & high-pressure centers. G = geostrophic wind, M_tan = gradient wind speed, M_ABLG = atmospheric-boundary-layer gradient wind speed. High-pressure centers cannot have strong pressure gradients; thus G is smaller

Eq. (10.33) is a quadratic equation that has two solutions. One solution is for the gradient wind Mtan around a cyclone (i.e., a low):

\(\ \begin{align} M_{\mathrm{tan}}=0.5 \cdot f_{c} \cdot R \cdot[-1+\sqrt{1+\dfrac{4 \cdot G}{f_{c} \cdot R}}]\tag{10.34a}\end{align}\)

The other solution is for flow around an anticyclone (i.e., a high):

\(\ \begin{align} M_{\mathrm{tan}}=0.5 \cdot f_{c} \cdot R \cdot[1-\sqrt{1-\dfrac{4 \cdot G}{f_{c} \cdot R}}]\tag{10.34b}\end{align}\)

To simplify the notation in the equations above, let

\(\ \begin{align} R o_{c}=\dfrac{G}{f_{c} \cdot R}\tag{10.35}\end{align}\)

where we can identify (Ro_c) as a “curvature” Rossby number because its length scale is the radius of curvature (R). When Ro_c is small, the winds are roughly geostrophic; namely, pressure gradient force nearly balances Coriolis force. [CAUTION: In later chapters you will learn about a Rossby radius of deformation, which is distinct from both Ro_c and R.]

For winds blowing around a low, the gradient wind is:

\(\ \begin{align} M_{\mathrm{tan}}=\dfrac{G}{2 \cdot R o_{c}} \cdot\left[-1+\left(1+4 \cdot R o_{c}\right)^{1 / 2}\right]\tag{10.36a}\end{align}\)

and for winds around a high) the gradient wind is:

\(\ \begin{align} M_{\mathrm{tan}}=\dfrac{G}{2 \cdot R o_{c}} \cdot\left[1-\left(1-4 \cdot R o_{c}\right)^{1 / 2}\right]\tag{10.36b}\end{align}\)

where G is the geostrophic wind.

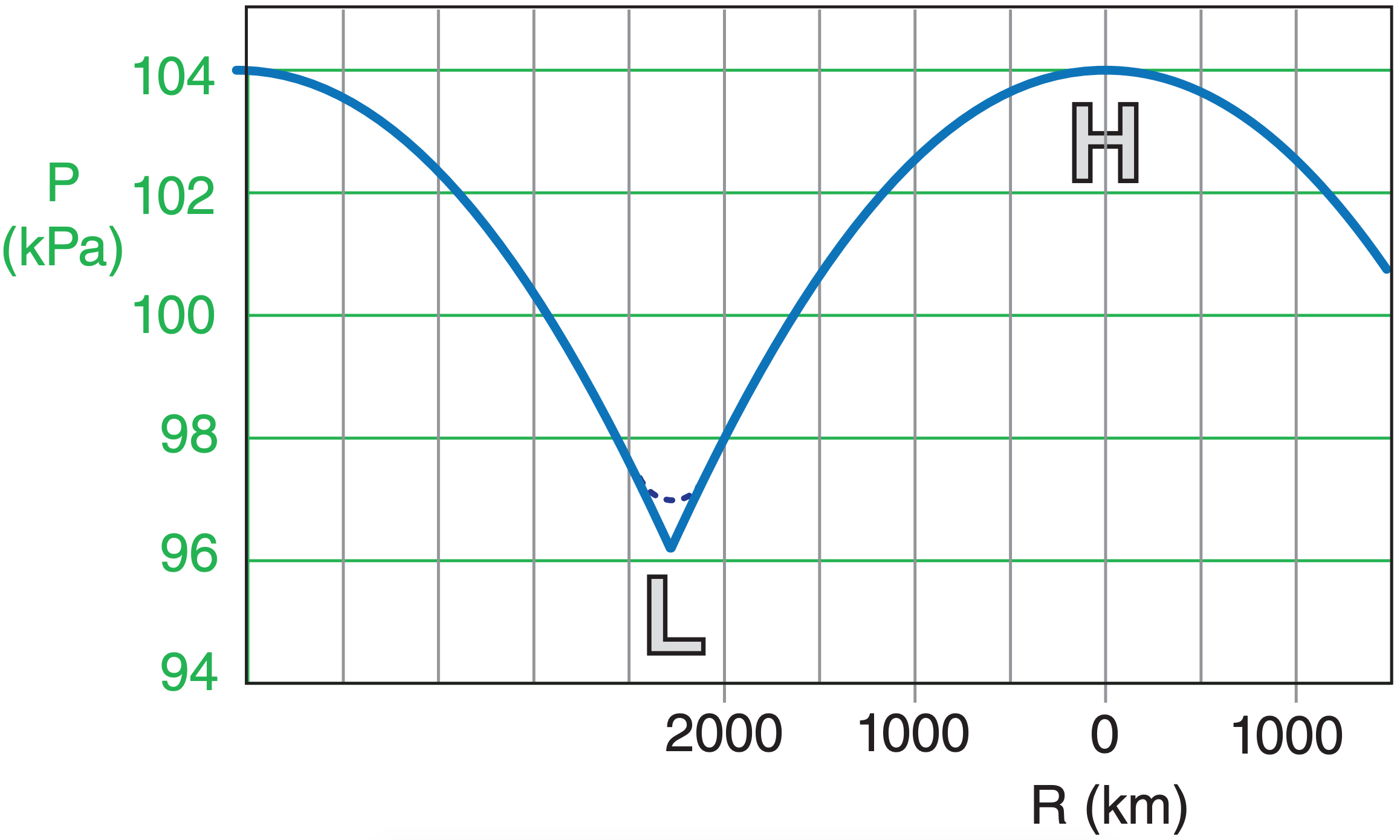
While the differences between solutions (10.36a & b) appear subtle at first glance, these differences have a significant impact on the range of winds that are physically possible. Any value of Ro_c can yield physically reasonable winds around a low-pressure center (eq. 10.36a). But to maintain a positive argument inside the square root of eq. (10.36b), only values of Ro_c ≤ 1/4 are allowed for a high.

Thus, strong radial pressure gradients with small radii of curvature, and strong tangential winds can exist near low center. But only weak pressure gradients with large radii of curvature and light winds are possible near high-pressure centers (Figs. 10.14 and 10.15). To find the maximum allowable horizontal variations of height z or pressure P near anticyclones, use Ro_c = 1/4 in eq. (10.35) with G from (10.29c) or (10.28):

\(\ \begin{align} z=z_{c}-\left(f_{c}^{2} \cdot R^{2}\right) /(8 \cdot|g|)\tag{10.37a}\end{align}\)

or

\(\ \begin{align} P=P_{c}-\left(\rho \cdot f_{c}^{2} \cdot R^{2}\right) / 8\tag{10.37b}\end{align}\)

where the center pressure in the high (anticyclone) is P_c , or for an isobaric surface the center height is z_c, the Coriolis parameter is f_c , |g| is gravitational acceleration magnitude, ρ is air density, and the radius from the center of the high is R (see Fig. 10.14).

Figs. 10.14 and 10.15 show that pressure gradients, and thus the geostrophic wind, can be large near low centers. However, pressure gradients, and thus the geostrophic wind, must be small near high centers. This difference in geostrophic wind speed G between lows and highs is sketched in Fig. 10.16. The slowdown of gradient wind M_tan (relative to geostrophic) around lows, and the speedup of gradient wind (relative to geostrophic) around highs is also plotted in Fig. 10.16. The net result is that gradient winds, and even atmospheric boundarylayer gradient winds M_ABLG (described later in this chapter), are usually stronger (in an absolute sense) around lows than highs. For this reason, low-pressure centers are often windy.

Sample Application

If G = 10 m s^–1, find the gradient wind speed & Ro_c, given f_c = 10^–4 s^–1 and a radius of curvature of 500 km?

Find the Answer

Given: G = 10 m s^–1, R = 500 km, f_c = 10^–4 s^–1

Find: M_tan = ? m s^–1, Ro_c = ? (dimensionless)

Use eq. (10.34a): M_tan = 0.5 · (10^-4s^-1) ·(500000m)·

\([-1+\sqrt{1+\dfrac{4 \cdot(10 m / s)}{\left(10^{-4} s^{-1}\right) \cdot(500000 m)}}]=\underline{8.54 m s^{-1}}\)

Use eq. (10.35):

\(R o_{c}=\dfrac{(10 \mathrm{m} / \mathrm{s})}{\left(10^{-4} \mathrm{s}^{-1}\right) \cdot\left(5 \times 10^{5} \mathrm{m}\right)}=\underline{0.2}\)

Check: Physics & units are reasonable.

Exposition: The gradient wind is slower than geostrophic and is in geostrophic balance.

Figure 10.17 Balance of forces (brown arrows) creating an atmospheric-boundary-layer wind (M_ABL, solid grey arrow) that is slower than geostrophic (G, hollow grey arrow). Thin green lines are isobars. L and H are low and high-pressure centers.

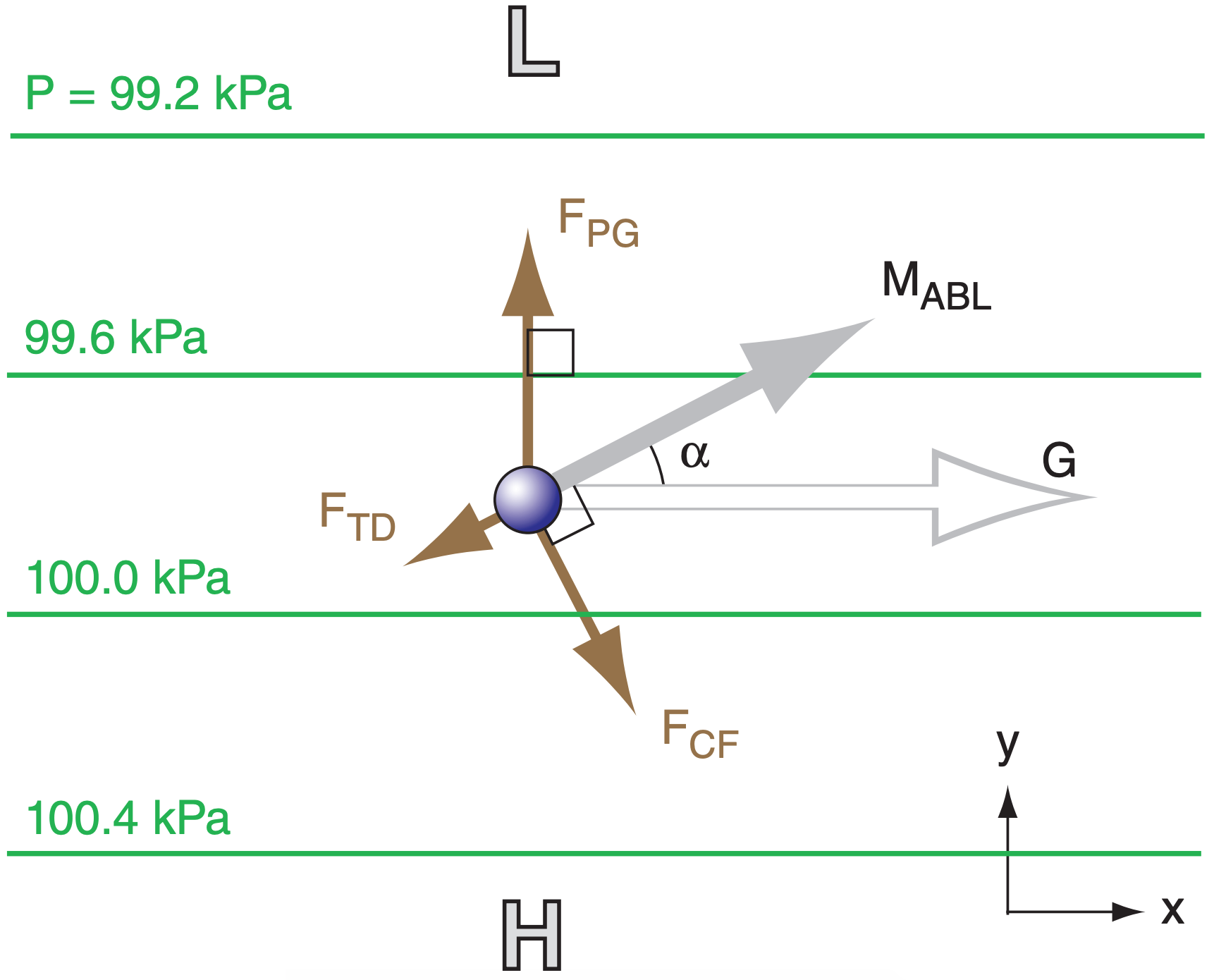
10.5.3. Atmospheric-Boundary-Layer Wind

If you add turbulent drag to winds that would have been geostrophic, the result is a subgeostrophic (slower-than-geostrophic) wind that crosses the isobars at angle (α) (Fig. 10.17). This condition is found in the atmospheric boundary layer (ABL) where the isobars are straight. The force balance at steady state is:

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta x}+f_{c} \cdot V-w_{T} \cdot \dfrac{U}{z_{i}}\tag{10.38a}\end{align}\)

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta y}-f_{c} \cdot U-w_{T} \cdot \dfrac{V}{z_{i}}\tag{10.38b}\end{align}\)

Namely, the only forces acting for this special case are pressure gradient, Coriolis, and turbulent drag (Fig. 10.17).

Replace U with U_ABL and V with V_ABL to indicate these winds are in the ABL. Eqs. (10.38) can be rearranged to solve for the ABL winds, but this solution is implicit (depends on itself):

\(\ \begin{align} U_{A B L}=U_{g}-\dfrac{w_{T} \cdot V_{A B L}}{f_{c} \cdot z_{i}}\tag{10.39a}\end{align}\)

\(\ \begin{align} V_{A B L}=V_{g}+\dfrac{w_{T} \cdot U_{A B L}}{f_{c} \cdot z_{i}}\tag{10.39b}\end{align}\)

where (U_g, V_g) are geostrophic wind components, f_c is Coriolis parameter, z_i is ABL depth, and w_T is the turbulent transport velocity.

You can iterate to solve eqs. (10.39). Namely, first you guess a value for V_ABL to use in the right side of the first eq. Solve eq. (10.39a) for U_ABL and use it in the right side of eq. (10.39b), which you can solve for V_ABL. Plug this back into the right side of eq. (10.39a) and repeat this procedure until the solution converges (stops changing very much). The magnitude of the boundary-layer wind is:

\(\ \begin{align} M_{A B L}=\left[U^{2} A B L+V^{2} A B L\right]^{1 / 2}\tag{10.40}\end{align}\)

For a statically neutral ABL under windy conditions, then w_T = C_D·M_ABL, where C_D is the drag coefficient (eq. 10.21). For most altitudes in the neutral ABL, an approximate but explicit solution is:

\(\ \begin{align} U_{A B L} \approx\left(1-0.35 \cdot a \cdot U_{g}\right) \cdot U_{g}-\left(1-0.5 \cdot a \cdot V_{g}\right) \cdot a \cdot V_{g} \cdot G\tag{10.41a}\end{align}\)

\(\ \begin{align} V_{A B L} \approx\left(1-0.5 \cdot a \cdot u_{g}\right) \cdot a \cdot G \cdot U_{g}+\left(1-0.35 \cdot a \cdot V_{g}\right) \cdot V_{g}\tag{10.41b}\end{align}\)

where the parameter is a = C_D/(f_c·z_i ), G is the geostrophic wind speed and a solution is possible only if a·G < 1. If this condition is not met, or if no reasonable solution can be found using eqs. (10.41), then use the iterative approach described in the next section, but with the centrifugal terms set to zero. Eqs. (10.41) do not apply to the surface layer (bottom 5 to 10% of the neutral boundary layer).

If the ABL is statically unstable (e.g., sunny with slow winds), use w_T = b_D·w_B (see eq. 10.22). Above the surface layer there is an exact solution that is explicit:

\(\ \begin{align} U_{A B L}=c_{2} \cdot\left[U_{g}-c_{1} \cdot V_{g}\right]\tag{10.42a}\end{align}\)

\(\ \begin{align} V_{A B L}=c_{2} \cdot\left[V_{g}+c_{1} \cdot U_{g}\right]\tag{10.42b}\end{align}\)

where \(c_{1}=\dfrac{b_{D} \cdot w_{B}}{f_{c} \cdot z_{i}},\) and \(c_{2}=\dfrac{1}{\left[1+c_{1}^{2}\right]}\)

The factors in c₁ are given in the “Forces” section.

In summary, both wind-shear turbulence and convective turbulence cause drag. Drag makes the ABL wind slower than geostrophic (subgeostrophic), and causes the wind to cross isobars at angle α such that it has a component pointing to low pressure.

Sample Application

For statically neutral conditions, find the winds in the boundary layer given: z_i = 1.5 km, U_g = 15 m s^–1, V_g = 0, f_c = 10^–4 s^–1, and C_D = 0.003. What is the crossisobar wind angle?

Find the Answer

Given: z_i = 1.5 km, U_g = 15 m s^–1, V_g = 0, f_c = 10^–4 s^–1, C_D = 0.003.

Find: V_ABL =? m s^–1, U_ABL =? m s^–1, M_ABL =? m s^–1, α = ? °

First: G =(U_g² + V_g²) 1/2 = 15 m s^–1. Now apply eq.(10.41)

\(a=\dfrac{0.003}{\left(10^{-4} \mathrm{s}^{-1}\right) \cdot(1500 \mathrm{m})}=0.02 \mathrm{s} / \mathrm{m}\)

Check: a·G = (0.02 s m^–1)·(15 m s^–1) =0.3 (is < 1. Good.)

U_ABL=[1–0.35·(0.02s m^–1)·(15m s^–1)]·(15m s^–1)≈13.4m s^–1

V_ABL=[1–0.5·(0.02s m^–1)·(15m s^–1)]· (0.02s m^–1)·(15m s^–1)·(15m s^–1) ≈ 3.8 m s^–1

\(M_{A B L}=\sqrt{U_{A B L}^{2}+V_{A B L}^{2}}=\sqrt{13.4^{2}+3.8^{2}}=13.9 \mathrm{ms}^{-1}\)

Isobars are parallel to the geostrophic wind. Thus, the cross-isobar angle is:

α =tan^–1(V_ABL/U_ABL) = tan^–1(3.8/13.4) = 15.8° .

Check: Physics & units are reasonable.

Exposition: Drag both slows the wind (13.4 m s^–1) in the boundary layer below its geostrophic value (15 m s^–1) and turns it at a small angle (15.8°) towards low pressure. Given N. Hem. (because of the positive Coriolis parameter), the ABL wind direction is 254.2°.

Sample Application

For statically unstable conditions, find winds in the ABL given V_g = 0, U_g = 5 m s^–1, w_B = 50 m s^–1, z_i = 1.5 km, b_D = 1.83x10^–3, and f_c = 10^–4 s^–1. What is the crossisobar wind angle?

Find the Answer

Given: (use convective boundary layer values above)

Find: M_ABL =? m s^–1, V_ABL =? m s^–1, U_ABL =? m s^–1, α =?°

Apply eqs. (10.42):

\(c_{1}=\dfrac{\left(1.83 \times 10^{-3}\right) \cdot(50 \mathrm{m} / \mathrm{s})}{\left(10^{-4} \mathrm{s}^{-1}\right) \cdot(1500 \mathrm{m})}=0.61(\) dimensionless)

c₂ = 1/[1+(0.61)²] = 0.729 (dimensionless)

U_ABL = 0.729·[(5m s^–1) – 0 ] = 3.6 m s^–1

V_ABL = 0.729·[0 + (0.61)·(5m s^–1)] = 2.2 m s^–1

Use eq. (10.40):

M_ABL = [U² _ABL + V² _ABL ]^1/2 = 4.2 m s^–1

α =tan^–1(V_ABL/U_ABL) = tan^–1(2.2/3.6) = 31.4°

Check: Physics & units are reasonable.

Exposition: Again, drag slows the wind and causes it to cross the isobars toward low pressure. The ABL wind direction is 238.6°.

10.5.4. ABL Gradient (ABLG) Wind

For curved isobars in the atmospheric boundary layer (ABL), there is an imbalance of the following forces: Coriolis, pressure-gradient, and drag. This imbalance is a centripetal force that makes ABL air spiral outward from highs and inward toward lows (Fig. 10.18). An example was shown in Fig. 10.1.

Figure 10.18 Imbalance of forces (brown arrows) yield a net centripetal force (F_net) that causes the atmospheric-boundary-layer gradient wind (M_ABLG, solid grey arrow) to be slower than both the gradient wind (M_tan) and geostrophic wind (G). The resulting air-parcel path crosses the isobars (green lines) at a small angle α toward low pressure.

If we devise a centrifugal force equal in magnitude but opposite in direction to the centripetal force, then the equations of motion can be written for spiraling flow that is steady over any point on the Earth’s surface (i.e., NOT following the parcel):

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta x}+f_{C} \cdot V-w_{T} \cdot \dfrac{U}{z_{i}}+s \cdot \dfrac{V \cdot M}{R}\tag{10.43a}\end{align}\)

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta y}-f_{c} \cdot u-w_{T} \cdot \dfrac{V}{z_{i}}-s \cdot \dfrac{U \cdot M}{R}\tag{10.43b}\end{align}\)

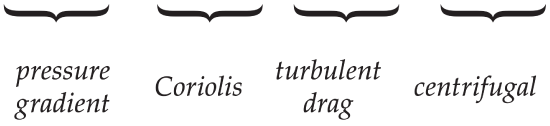
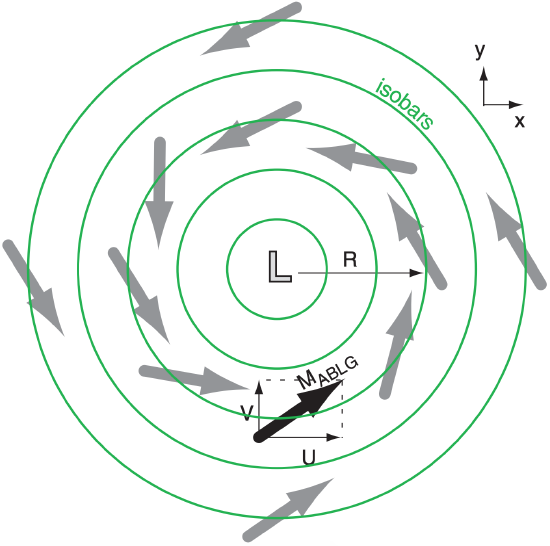
We can anticipate that the ABLG winds should be slower than the corresponding gradient winds, and should cross isobars toward lower pressure at some small angle α (see Fig. 10.19).

Figure 10.19 Tangential ABLG wind component (U) and radial ABLG wind component (V) for the one vector highlighted as the thick black arrow. N. Hemisphere.

Lows are often overcast and windy, implying that the atmospheric boundary layer is statically neutral. For this situation, the transport velocity is given by:

\(\ \begin{align} w_{\mathrm{T}}=C_{D} \cdot M=C_{D} \cdot \sqrt{U^{2}+V^{2}}\tag{10.21 again}\end{align}\)

Because this parameterization is nonlinear, it increases the nonlinearity (and the difficulty to solve), eqs. (10.43).

Highs often have mostly clear skies with light winds, implying that the atmospheric boundary layer is statically unstable during sunny days, and statically stable at night. For daytime, the transport velocity is given by:

\(\ \begin{align} w_{T}=b_{D} \cdot w_{B}\tag{10.22 again}\end{align}\)

This parameterization for w_B is simple, and does not depend on wind speed. For statically stable conditions during fair-weather nighttime, steady state is unlikely, meaning that eqs. (10.43) do not apply.

Nonlinear coupled equations (10.43) are difficult to solve analytically. However, we can rewrite the equations in a way that allows us to iterate numerically toward the answer (see the INFO box below for instructions). The trick is to not assume steady state. Namely, put the tendency terms (∆U/∆t , ∆V/∆t) back in the left hand sides (LHS) of eqs. (10.43). But recall that ∆U/∆t = [U(t+∆t) – U]/∆t, and similar for V.

For this iterative approach, first re-frame eqs. (10.43) in cylindrical coordinates, where (U, V) are the (tangential, radial) components, respectively (see Fig. 10.19). Also, use G, the geostrophic wind definition of eq. (10.28), to quantify the pressure gradient.

For a cyclone in the Northern Hemisphere (for which s = +1 from Table 10-2), the atmospheric boundary layer gradient wind eqs. (10.43) become:

\(\ \begin{align} M=\left(U^{2}+V^{2}\right)^{1 / 2}\tag{1.1 again}\end{align}\)

\(\ \begin{align} U(t+\Delta t)=U+\Delta t \cdot\left[f_{c} \cdot V-\dfrac{C_{D} \cdot M \cdot U}{z_{i}}+s \dfrac{V \cdot M}{R}\right]\tag{10.44a}\end{align}\)

\(\ \begin{align} V(t+\Delta t)=V+\Delta t \cdot\left[f_{c} \cdot(G-U)-\dfrac{C_{D} \cdot M \cdot V}{z_{i}}-s \dfrac{U \cdot M}{R}\right]\tag{10.44b}\end{align}\)

where (U, V) represent (tangential, radial) parts for the wind vector south of the low center. These coupled equations are valid both night and day.

Sample Application

If G = 10 m s^–1 at R = 400 km from the center of a N. Hem. cyclone, C_D = 0.02, z_i = 1 km, and fc = 10^–4 s^–1, then find the ABLG wind speed and components.

Find the Answer

Given: (see the data above)

Find: M_BLG = ? m s^–1, U_BLG = ? m s^–1, V_BLG = ? m s^–1,

Use a spreadsheet to iterate (as discussed in the INFO box) eqs. (10.44) & (1.1) with a time step of ∆t = 1200 s. Use U = V = 0 as a first guess.

G (m/s)=	10		zi (km)=	1
R (km)=	400		fc (s^–1)=	0.0001
CD =	0.02		∆t(s)=	1200
Iteration	UABLG	VABLG	MABLG	∆UABLG	∆ VABLG
Counter	(m s^–1)	(m s^–1)	(m s^–1)	(m s^–1)	(m s^–1)
0	0.00	0.00	0.00	0.000	1.200
1	0.00	1.20	1.20	0.148	1.165
2	0.15	2.37	2.37	0.292	1.047
3	0.44	3.41	3.44	0.408	0.861
4	0.85	4.27	4.36	0.480	0.640
5	1.33	4.91	5.09	0.502	0.420
. . .
29	4.16	4.33	6.01	-0.003	0.001
30	4.16	4.33	6.01	-0.002	0.001

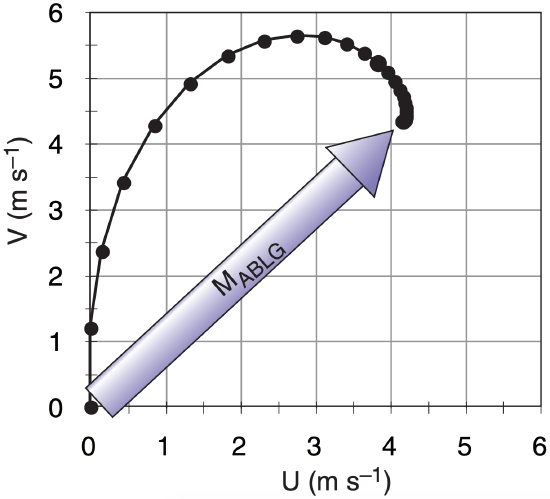The evolution of the iterative solution is plotted at right as it approaches the final answer of U_ABLG = 4.16 m s^–1, V_ABLG = 4.33 m s^–1, M_ABLG= 6.01 m s^–1, where (U_ABLG , V_ABLG) are (tangential, radial) parts.

Check: Physics & units are reasonable. You should do the following “what if” experiments on the spreadsheet to check the validity. I ran experiments using a modified spreadsheet that relaxed the results using a weighted average of new and previous winds.

(a) As R approaches infinity and C_D approaches zero, then M_ABLG should approach the geostrophic wind G. I got U_ABLG = G = 10 m s^–1, V_ABLG = 0.

(b) For finite R and 0 drag, then M_ABLG should equal the gradient wind M_tan. I got U_ABLG = 8.28 m s^–1, V_ABLG = 0.

(c) For finite drag but infinite R, then M_ABLG should equal the atmospheric boundary layer wind M_ABL. I got U_ABLG = 3.91 m s^–1, V_ABLG = 4.87 m s^–1. Because this ABL solution is based on the full equations, it gives a better answer than eqs. (10.41).

Exposition: If you take slightly larger time steps, the solution converges faster. But if ∆t is too large, the iteration method fails (i.e., blows up).

INFO • Find the Answer by Iteration

(1) Make an initial guess for (U, V), such as (0, 0).

(2) Use these (U, V) values in the right sides of eqs. (10.44) and (1.1), and solve for the new values of [U(t+∆t), V(t+∆t)].

(3) In preparation for the next iteration, let U = U(t+∆t) , and V = V(t+∆t) .

(4) Repeat steps 2 and 3 using the new (U, V) on the right hand sides .

(5) Keep iterating. Eventually, the [U(t+∆t), V(t+∆t)] values stop changing (i.e., reach steady state), giving UABLG = U(t+∆t), and VABLG = V(t+∆t).

Because of the repeated, tedious calculations, I recommend you use a spreadsheet (see the Sample Application) or write your own computer program.

As you can see from the Sample Application, the solution spirals toward the final answer as a damped inertial oscillation.

For daytime fair weather conditions in anticyclones, you could derive alternatives to eqs. (10.44) that use convective parameterizations for atmospheric boundary layer drag.

Because eqs. (10.44) include the tendency terms, you can also use them for non-steady-state (time varying) flow. One such case is nighttime during fair weather (anticyclonic) conditions. Near sunset, when vigorous convective turbulence dies, the drag coefficient suddenly decreases, allowing the wind to accelerate toward its geostrophic equilibrium value. However, Coriolis force causes the winds to turn away from that steady-state value, and forces the winds into an inertial oscillation. See a previous INFO box titled Approach to Geostrophy for an example of undamped inertial oscillations.

During a portion of this oscillation the winds can become faster than geostrophic (supergeostrophic), leading to a low-altitude phenomenon called the nocturnal jet. See the Atmospheric Boundary Layer chapter for details.

10.5.5. Cyclostrophic Wind

Winds in tornadoes are about 100 m s^–1, and in waterspouts are about 50 m s^–1. As a tornado first forms and tangential winds increase, centrifugal force increases much more rapidly than Coriolis force. Centrifugal force quickly becomes the dominant force that balances pressure-gradient force (Fig. 10.20). Thus, a steady-state rotating wind is reached at much slower speeds than the gradient wind speed.

Figure 10.20 Around tornadoes, pressure gradient force F_PG is so strong that it greatly exceeds all other forces such as Coriolis force F_CF. The net force (F_net) pulls the air around the tight circle at the cyclostrophic wind speed (M_cs).

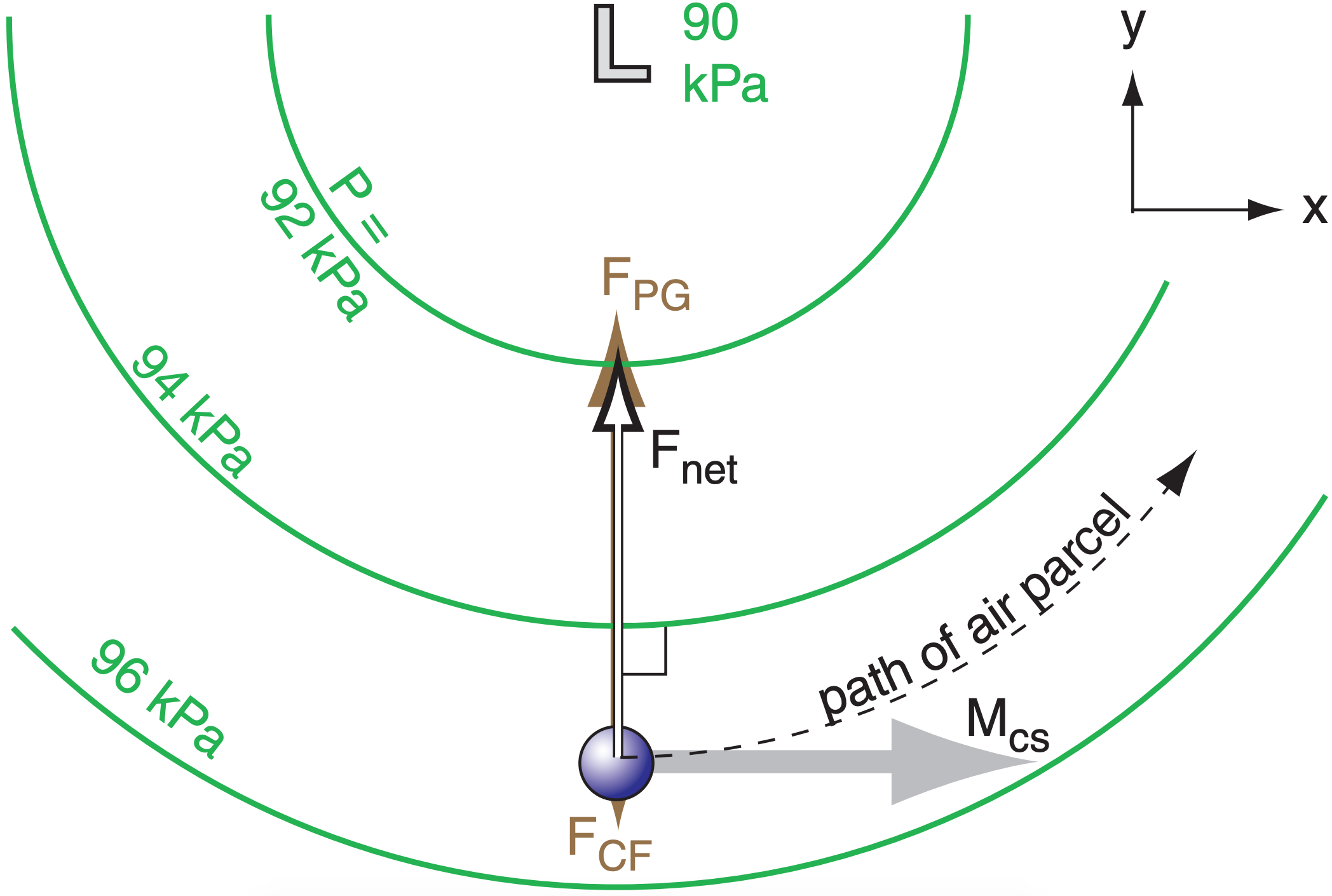
If the tangential velocity around the vortex is steady, then the steady-state force balance is:

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta x}+s \cdot \dfrac{V \cdot M}{R}\tag{10.45a}\end{align}\)

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta y}-s \cdot \dfrac{U \cdot M}{R}\tag{10.45b}\end{align}\)

You can use cylindrical coordinates to simplify solution for the cyclostrophic (tangential) winds M_cs around the vortex. The result is:

\(\ \begin{align} M_{c s}=\sqrt{\dfrac{R}{\rho} \cdot \dfrac{\Delta P}{\Delta R}}\tag{10.46}\end{align}\)

where the velocity M_cs is at distance R from the vortex center, and the radial pressure gradient in the vortex is ∆P/∆R.

Recall from the Gradient Wind section that anticyclones cannot have strong pressure gradients, hence winds around highs are too slow to be cyclostrophic. Around cyclones (lows), cyclostrophic winds can turn either counterclockwise or clockwise in either hemisphere, because Coriolis force is not a factor.

Sample Application

A 10 m radius waterspout has a tangential velocity of 45 m s^–1. What is the radial pressure gradient?

Find the Answer

Given: M_cs = 45 m s^–1, R = 10 m.

Find: ∆P/∆R = ? kPa m^–1.

Assume cyclostrophic wind, and ρ = 1 kg m^–3.

Rearrange eq. (10.46):

\(\dfrac{\Delta P}{\Delta R}=\dfrac{\rho}{R} \cdot M_{c s}^{2}=\dfrac{\left(1 \mathrm{kg} / \mathrm{m}^{3}\right) \cdot(45 \mathrm{m} / \mathrm{s})^{2}}{10 \mathrm{m}}\)

∆P/∆R = 202.5 kg·m^–1·s^–2 / m = 0.2 kPa m^–1.

Check: Physics & units are reasonable.

Exposition: This is 2 kPa across the 10 m waterspout radius, which is 1000 times greater than typical synoptic-scale pressure gradients on weather maps.

10.5.6. Inertial Wind

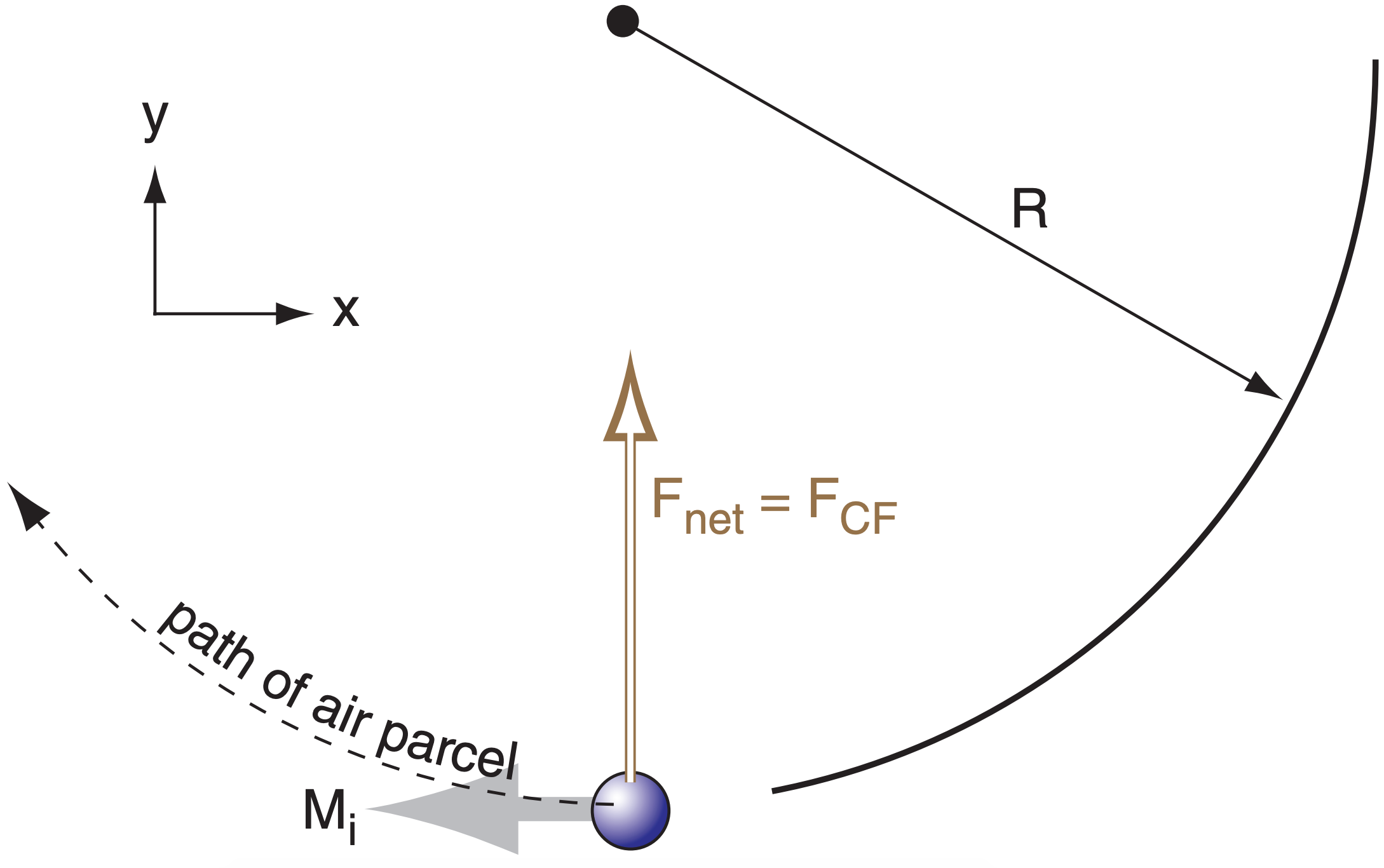
Steady-state inertial motion results from a balance of Coriolis and centrifugal forces in the absence of any pressure gradient:

\(\ \begin{align} 0=f_{c} \cdot M_{i}+\dfrac{M_{i}^{2}}{R}\tag{10.47}\end{align}\)

where M_i is inertial wind speed, f_c is the Coriolis parameter, and R is the radius of curvature. Since both of these forces depend on wind speed, the inertial wind cannot start itself from zero. It can occur only after some other force first causes the wind to blow, and then that other force disappears.

The inertial wind coasts around a circular path of radius R,

\(\ \begin{align} R=-\dfrac{M_{i}}{f_{c}}\tag{10.48}\end{align}\)

where the negative sign implies anticyclonic rotation (Fig. 10.21). The time period needed for this inertial oscillation to complete one circuit is Period = 2π/f_c, which is half of a pendulum day (see Approach to Geostrophy INFO Box earlier in this chapter).

Although rarely observed in the atmosphere, inertial oscillations are frequently observed in the ocean. This can occur where wind stress on the ocean surface creates an ocean current, and then after the wind dies the current coasts in an inertial oscillation.

Figure 10.21 Coriolis force (F_CF, thick brown arrow, behind the white arrow) on an air parcel (blue ball), creating an anticyclonic inertial wind M_i , grey arrow). R is radius of curvature. White arrow is net force F_net.

Sample Application

For an inertial ocean current of 5 m s^–1, find the radius of curvature and time period to complete one circuit. Assume a latitude where fc = 10^–4 s^–1.

Find the Answer

Given: M_i = 5 m s^–1, f_c = 10^–4 s^–1.

Find: R = ? km, Period = ? h

Use eq. (10.48): R = –(5 m s^–1) / (10^–4 s^–1) = –50 km

Use Period = 2π/f_c = 62832 s = 17.45 h

Check: Units & magnitudes are reasonable.

Exposition: The tracks of drifting buoys in the ocean are often cycloidal, which is the superposition of a circular inertial oscillation and a mean current that gradually translates (moves) the whole circle.

10.5.7. Antitriptic Wind

A steady-state antitriptic wind Ma could result from a balance of pressure-gradient force and turbulent drag:

\(\ \begin{align} 0=-\dfrac{1}{\rho} \cdot \dfrac{\Delta P}{\Delta d}-w_{T} \cdot \dfrac{M_{a}}{z_{i}}\tag{10.49}\end{align}\)

where ∆P is the pressure change across a distance ∆d perpendicular to the isobars, w_T is the turbulent transport velocity, and z_i is the atmospheric boundary-layer depth.

Figure 10.22 Balance of forces (F, brown arrows) that create the antitriptic wind M_a (grey arrow). G is the theoretical geostrophic wind. F_TD is turbulent drag, and F_PG is pressure-gradient force.

This theoretical wind blows perpendicular to the isobars (Fig. 10.22), directly from high to low pressure:

\(\ \begin{align} M_{a}=\dfrac{z_{i} \cdot f_{c} \cdot G}{w_{T}}\tag{10.50}\end{align}\)

For free-convective boundary layers, w_T = b_D·w_B is not a function of wind speed, so M_a is proportional to G. However, for windy forced-convection boundary layers, w_T = C_D·M_a, so solving for Ma shows it to be proportional to the square root of G.

This wind would be found in the atmospheric boundary layer, and would occur as an along-valley component of “long gap” winds (see the Regional Winds chapter). It is also sometimes thought to be relevant for thunderstorm cold-air outflow and for steady sea breezes. However, in most other situations, Coriolis force should not be neglected; thus, the atmospheric boundary-layer wind and BL Gradient winds are much better representations of nature than the antitriptic wind.

Sample Application

In a 1 km thick convective boundary layer at a location where f_c = 10^–4s^–1, the geostrophic wind is 5 m s^–1. The turbulent transport velocity is 0.02 m s^–1. Find the antitriptic wind speed.

Find the Answer

Given: G = 5 m s^–1, z_i = 1000 m, f_c = 10^–4 s^–1, w_T = 0.02 m s^–1

Find: M_a = ? m s^–1

Use eq. (10.50):

M_a = (1000m)·(10^–4 s^–1)·(5m s^–1) / (0.02 m s^–1) = 25 m s^–1

Check: Magnitude is too large. Units reasonable.

Exposition: Eq. (10.50) can give winds of M_a > G for many convective conditions, for which case Coriolis force would be expected to be large enough that it should not be neglected. Thus, antitriptic winds are unphysical. However, for forced-convective boundary layers where drag is proportional to wind speed squared, reasonable solutions are possible.

10.5.8. Summary of Horizontal Winds

Table 10-5 summarizes the idealized horizontal winds that were discussed earlier in this chapter.

On real weather maps such as Fig. 10.23, isobars or height contours have complex shapes. In some regions the height contours are straight (suggesting that actual winds should nearly equal geostrophic or boundary-layer winds), while in other regions the height contours are curved (suggesting gradient or boundary-layer gradient winds). Also, as air parcels move between straight and curved regions, they are sometimes not quite in equilibrium. Nonetheless, when studying weather maps you can quickly estimate the winds using the summary table.

Figure 10.23 One-day average geopotential heights z (thick lines in km, thin lines in m) on the 20 kPa isobaric surface for 5 Feb 2013. Close spacing (tight packing) of the height contours indicate faster winds. This upper-level chart is for the same day and location (Atlantic Ocean) as the mean-sea-level pressure chart in Fig. 10.15. [Courtesy of NOAA/NCEP Earth System Research Lab. http://www.esrl.noaa.gov/psd/data/gr...eanalysis.html ]

Table 10-5. Summary of horizontal winds**.
Item	Name of Wind	Forces	Direction	Magnitude	Where Observed
1	geostrophic	pressure-gradient, Coriolis	parallel to straight isobars with Low pressure to the wind’s left*	faster where isobars are closer together. \(G=\left|\dfrac{g}{f_{c}} \cdot \dfrac{\Delta z}{\Delta d}\right|\)	aloft in regions where isobars are nearly straight
2	gradient	pressure-gradient, Coriolis, centrifugal	similar to geostrophic wind, but following curved isobars. Clockwise* around Highs, counterclockwise* around Lows.	slower than geostrophic around Lows, faster than geostrophic around Highs	aloft in regions where isobars are curved
3	atmospheric boundary layer	pressure-gradient, Coriolis, drag	similar to geostrophic wind, but crosses isobars at small angle toward Low pressure	slower than geostrophic (i.e., subgeostrophic)	near the ground in regions where isobars are nearly straight
4	atmospheric boundarylayer gradient	pressure-gradient, Coriolis, drag, centrifugal	similar to gradient wind, but crosses isobars at small angle toward Low pressure	slower than gradient wind speed	near the ground in regions where isobars are curved
5	pressure-gradient, centrifugal	pressure-gradient, centrifugal	either clockwise or counterclockwise around strong vortices of small diameter	stronger for lower pressure in the vortex center	tornadoes, waterspouts (& sometimes in the eye-wall of hurricanes)
6	inertial	Coriolis, centrifugal	anticyclonic circular rotation	coasts at constant speed equal to its initial speed	ocean-surface currents

* For Northern Hemisphere. Direction is opposite in Southern Hemisphere. ** Antitriptic winds are unphysical; not listed here.