10.4: Equations of Horizontal Motion
- Page ID
- 9592
Combining the forces from eqs. (10.7, 10.8, 10.9, 10.17, and 10.19) into Newton’s Second Law of Motion (eq. 10.5) gives simplified equations of horizontal motion:
\(\ \begin{align} \frac{\Delta U}{\Delta t}=-U \frac{\Delta U}{\Delta x}-V \frac{\Delta U}{\Delta y}-W \frac{\Delta U}{\Delta z}-\frac{1}{\rho} \cdot \frac{\Delta P}{\Delta x}+f_{c} \cdot V-w_{T} \cdot \frac{U}{z_{i}}\tag{10.23a}\end{align}\)
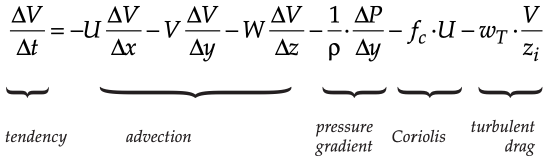 (10.23b)
(10.23b)
These are the forecast equations for wind.
For special conditions where steady winds around a circle are anticipated, centrifugal force can be included.
The terms on the right side of eqs. (10.23) can all be of order 1x10–4 to 10x10–4 m·s–2 (which is equivalent to units of N kg–1, see Appendix A for review). However, some of the terms can be neglected under special conditions where the flow is less complicated. For example, near-zero Coriolis force occurs near the equator. Near-zero turbulent drag exists above the ABL. Near-zero pressure gradient is at low- and high-pressure centers.
Other situations are more complicated, for which additional terms should be added to the equations of horizontal motion. Within a few mm of the ground, molecular friction is large. Above mountains during windy conditions, mountain-wave drag is large. Above the ABL, cumulus clouds and thunderstorms can create strong convective mixing.
For a few idealized situations where many terms in the equations of motion are small, it is possible to solve those equations for the horizontal wind speeds. These theoretical winds are presented in the next section. Later in this chapter, equations to forecast vertical motion (W) will be presented.


