15.2: Modes of Deposition
- Page ID
- 4247
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
This section examines local modes of sediment deposition. Some of these modes may be observable in laboratory experiments or in field studies. Others may be difficult or impossible to observe with present technology, and we can only make deductions or speculations about them. (Keep in mind that deductions can be very dangerous in physical sedimentology, because the physics of the phenomena are so complex that we can easily fool ourselves into thinking that an unimportant process is important or that an important process is unimportant.) The treatment will be entirely qualitative.
Several distinctive modes of deposition, discussed in the sections below, can be recognized. These modes grade into one another; there are no sharp boundaries among the various processes involved. Keep in mind also that the terms used for these modes are only unofficial; you are not likely to find them in the published literature on sediment deposition. See Figure \(\PageIndex{1}\) for cartoons that illustrate the various modes of deposition.
Fallout Without Traction
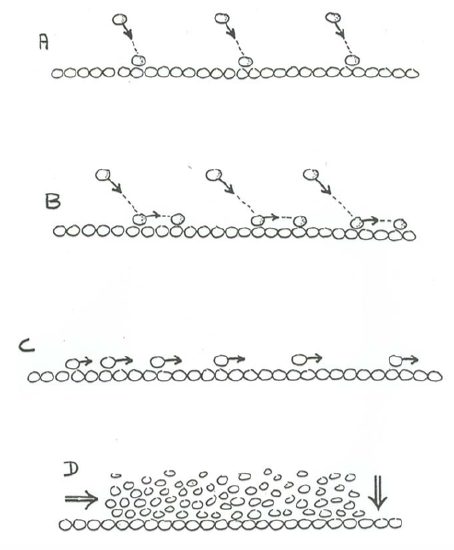
In the simplest of depositional modes, sediment particles suspended in a flow by some earlier process or event settle to the bed and are not transported thereafter, either by traction or by suspension (Figure \(\PageIndex{1}\)A). This might be called fallout without traction.
Flows that deposit sediment by fallout without traction have velocities below the threshold for bed-load transport, which ranges from slightly less than \(0.2\) \(\mathrm{m/s}\) to well over \(0.3\) \(\mathrm{m/s}\), depending on the depth of the flow and the size of the sediment particles. In general, the weaker the flow, the finer the sediment that is being carried and deposited in this mode. The flow may even be nonexistent; in that case, the sediment must be supplied directly from above, as for example by fallout of eolian sediment into a standing body of water.
The size of the sediment deposited by fallout without traction is usually very fine, seldom coarser than very fine sand. The reason is that the flow would need to be much stronger to carry coarser sediment in suspension, and such flows would be strong enough to move the deposited sediment as bed load after the sediment lands on the bed.
In fallout without traction, the thickness of deposit is limited only by the quantity of sediment in suspension above the bed. At first thought this might seem like a severe limitation, but remember that there can be sedimentation systems in which new sediment in suspension is introduced continuously some- where upcurrent in a steady flow (or, if not steady, episodic but long-continued), like an area offshore of the delta of a river carrying abundant suspended sediment. On the other hand, there is a definite spatial constraint: the downcurrent distance over which such deposition takes place is limited by the downstream loss of sediment from the flow. The finer the suspended sediment and the deeper the flow, the greater the distance over which there is deposition.
Fallout Without Traction
Sediment particles may settle onto the sediment bed from suspension and then be moved as bed load, or even be resuspended temporarily, before they eventually come to permanent rest and are buried by other particles as the bed builds up (Figure \(\PageIndex{1}\)B). This might be called fallout with traction.
Flows that deposit sediment by fallout with traction can have a wide range of velocities, from a small fraction of a meter per second to much greater than a few meters per second. Sediment size can range from silts to gravels. The only condition is that the flow is not so overloaded with suspended sediment that a well defined sediment–water interface cannot be maintained. The spatial and temporal constraints on the mode of deposition are largely the same as for fallout without traction.
Differential Transport
To non-geologists (and to some geologists as well!), if you mention deposition, what flashes into their minds is the kind of thing that happens when you suspend some sediment in a vessel of water and let it settle to the bottom. That was called, in the earlier section, fallout without traction. Yes, that is one mode of deposition, and it is important in many natural sedimentary environments. But there is an equally important mode of deposition that is much less intuitive. A sediment deposit can be formed without any fallout from suspension. At first thought this might seem strange, so we need to spend a little more time discussing this mode of deposition. Think about the consequences of a downstream change in sediment transport rate in a steady flow.
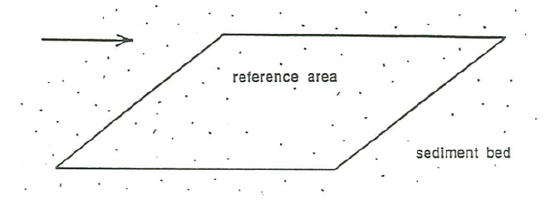
Look at a small rectangular reference area on the sediment bed beneath a flow that is transporting sediment over the bed (Figure \(\PageIndex{2}\)). The edges of the reference area are parallel to and perpendicular to the flow direction. Because volume of sediment is neither created nor destroyed on the short time scales associated with sediment transport by traction or suspension, we can invoke the principle of conservation of sediment volume in accounting for what happens to the sediment.
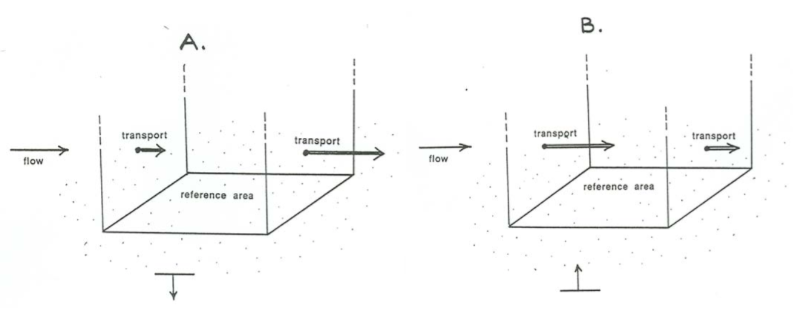
If the total volume of sediment in traction and suspension passing across the plane extending upward from the upstream edge of the reference area is less than the total volume of sediment passing across the plane extending upward from the downstream edge of the reference area (Figure \(\PageIndex{3}\)A), then sediment is somehow being added to the flow in the space above the reference area. The only place where that added sediment can come from is from the bed, and the only place where it can go is into the flow. So there must be net erosion of the bed.
On the other hand, if the total volume of sediment in traction and suspension passing across the upstream plane is greater than the total volume passing across the downstream plane (Figure 15-3B), then sediment is somehow being extracted from the flow in the space over the reference area. The only place where that extracted sediment can go is onto the bed, so there has to be net deposition on the bed. This mode of deposition might be called deposition by differential transport (Figure \(\PageIndex{1}\)C). Figure \(\PageIndex{4}\) shows, in cartoon form, the conditions for deposition by differential transport.
The consequence of the reasoning presented above is that there can be deposition on a sediment bed without any temporal change in the picture of sediment transport: the flow is steady, and the load and the sediment transport rate at every point do not change with time. There can be deposition, however, provided that the sediment transport rate is changing spatially by decreasing in the downstream direction.
Deposition by differential transport can take place entirely by downstream decrease in bed-load transport rate, even without any suspended sediment in the flow. This happens wherever the flow deepens slightly in the downstream direction (for any one or more of several reasons, which I will not discuss here), causing the flow velocity and therefore also the bed-load sediment transport rate to decrease in the downstream direction.
Flows that deposit sediment by differential transport range widely in flow velocity, from a few tenths of a meter per second to well over two meters per second. Sediment size ranges from finer than sand size to well into the gravel size range. Clearly, the coarser the sediment the more likely it is that the process involves differential bed-load transport rather than differential suspended-load transport.
As with deposition by fallout, there are constraints on both the thickness and the downstream extent of deposition by differential transport, but they are not exactly the same as for deposition by fallout. For a given value of “input” transport rate (that is, at the upstream end of the reach of flow that is experiencing downstream-decreasing transport rate), there must be an inverse relationship between the distance along which there is deposition and the rate of deposition at points along the transport path—basically because deposition is everywhere using up the stock of sediment that is in transport. This will have application to the geometry and interpretation of cross-stratification produced by bed forms in unidirectional and combined flows; see Chapter 16.
Keep in mind also that deposition can be by a combination of fallout and differential transport. These two cases are only end members of a continuous spectrum of possibilities, depending upon the particular depositional setting (that is, the nature of the sediment supply and the nature of the current).
Mass Deposition
In many flows, the concentration of sediment is so high that there is no strong distinction, in sediment concentration or particle fabric, between the flow and the underlying immobile bed. In such cases it is common for deposition to take place by sudden or gradual freezing or immobilization of the flow. I will call this mode of deposition mass deposition (Figure \(\PageIndex{1}\)D). This is in contrast to deposition by gradual buildup of the sediment bed when there is a well defined sediment-water interface. Mass deposition, discussed in this section, can therefore be counterposed to what might be called interfacial deposition, discussed in the preceding three sections. Treatment of the various processes involved in mass deposition, and the sedimentary textures and structures of the resulting deposits, are outside the scope of these course notes. The following brief comments will have to suffice.
Conditions during mass deposition are difficult to observe, because sediment concentrations are high and deposition is rapid. Also, the flows from which mass deposition occurs tend to be more powerful and on much larger scales than is the case with the other modes of deposition discussed above. Mass deposition is characteristic of strong sediment gravity flows, especially in their earlier stages.
It is my belief that mass deposition is important in two different but closely related depositional settings, both associated with sediment gravity flows:
- mass deposition at the base of a heavily laden turbidity current
- mass deposition by freezing of a classical debris flow, from the top down
Here are some brief comments about each of these settings.
When the region of the flow near the bed is overloaded with a high concentration of suspended sediment, as near the base of a large and powerful turbidity current carrying a high concentration of sediment both coarse and fine, the sediment settles to the bed with little space between adjacent sediment particles. A layer of the flow with a thickness that's orders of magnitude greater than the particle size becomes immobilized almost simultaneously as the shearing of the highly concentrated sediment-water mixture ceases (Figure \(\PageIndex{5}\)).
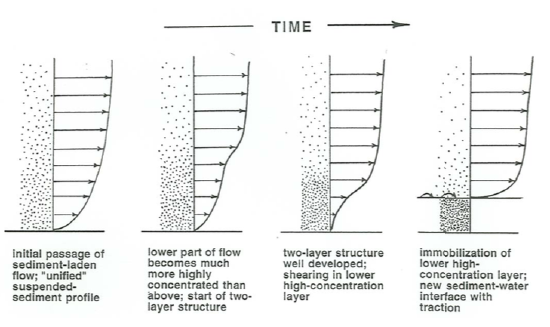
During such mass deposition there is no well defined sediment–water interface; instead there is a gradual transition between the underlying already- deposited bed and the sheared, highly concentrated suspension above. Another way of looking at this is that the pore-water content of the mixture varies continuously upward from the already-deposited sediment bed into the still-moving sediment–water mixture.
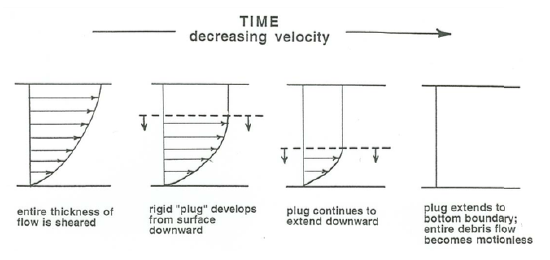
The other setting for mass deposition is that of a high-concentration debris flow, in which the sediment concentration is near the “choke point” (the maximum possible for which the sediment–water mixture can still undergo shearing without the particles locking together). The mechanical properties of a debris flow are very different from those of clear water, but the velocity profile is qualitatively the same, in that the rate of shearing increases from zero at the free surface to a maximum at the base Note that the velocity profile is perpendicular to the bottom boundary at the surface and becomes more and more nearly parallel to the bottom boundary with depth in the flow. This is because at deeper and deeper levels in the flow, there is a greater and greater weight of overlying fluid that drives the fluid overlying the shear plane at that level in the downchannel direction. Also, highly concentrated mixtures of sediment and water are different from clear water also by having shear strength: it takes a certain nonzero shear stress acting across the shear planes for shearing movement to take place. The consequence for thick and highly concentrated debris flows is that as the flow decelerates it freezes from the top down, and when the freezing reaches the base, the flow comes to a halt (Figure \(\PageIndex{6}\)), whereafter it sits motionless and slowly dewaters.