15.3: Why Deposition or Erosion?
- Page ID
- 4248
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
This section provides some background on the basic nature of deposition and erosion. Some of it might seem elementary to you, but a clear understanding of it is fundamental to a productive view of the nature of sediment deposition and erosion. In this section, I will use the terms aggradation for increase in bed-surface elevation during deposition, and degradation for decrease in bed-surface elevation during erosion.
A Broad View of Sediment Deposition
Take as broad a view of sediment deposition as possible (Figure \(\PageIndex{1}\)): sediment is derived from a source, mobilized, transported along a transport path, and deposited somewhere, which you could think of a sink. This is simple and elegant—but there is much more here than you might assume, at first thought.
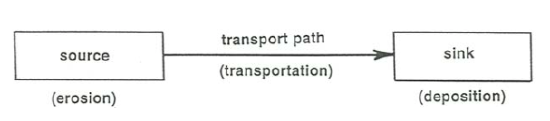
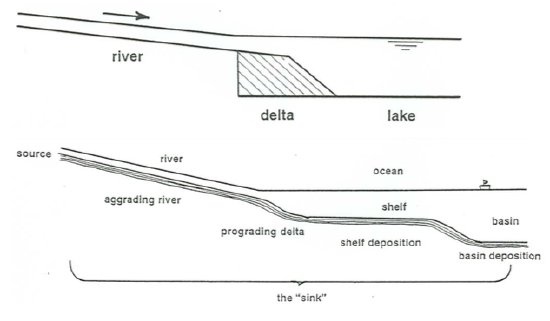
Sometimes the deposition is abrupt, as in the case of a Gilbert-style delta where a stream debouches into a lake Figured \(\PageIndex{2}\)A). More commonly, deposition is gradual, in a spatial sense: it is spread out over a long distance. Figure \(\PageIndex{2}\)B shows a common and important example.
The Relationship Between the Load and the Deposit
This subsection makes some fundamental points about the relationship between the sediment load and the deposit in a depositing flow. In my opinion, this material is fundamental to understanding the texture of a deposit, although it is not likely to tell you anything really practical.
Obviously (but importantly), whenever a deposit is being formed by a sediment-transporting flow, some percentage of the sediment load is being extracted from the flow and added to the bed, by one or more of the various processes discussed in the previous section. The ratio of sediment extraction to sediment passage or throughput can range from nearly zero, in the case of an almost uniform flow carrying fairly high concentrations of sediment in an almost nondepositional regime, to one hundred percent, when a flow dumps all its sediment in one place, as with certain kinds of debris flows. Just for convenience, I will call this ratio—unofficially—the deposition ratio. (Do not worry about how this ratio could be defined quantitatively.) Although you cannot read the value of the deposition ratio directly from beds in an outcrop, I think that it is one more of those things that are useful to think about as an aid in framing your interpretations.
This section deals with the relationship between the characteristics of the sediment load and the characteristics of the deposit left by the flow. As you learned back in Chapter 13, the sediment—whether in the substrate, in the active layer, on the bed surface, or in the sediment load—always has some joint probability distribution of particle size, particle shape, and particle density. You can never really characterize this distribution fully, even when you can obtain a good representative sample of the load, mainly because of the problem of the infinite variations in particle shape, but it is nonetheless real, and important.
When deposition takes place, some subset of the passing particles are selected from the flow to become part of the permanent deposit left behind by the flow. Here is what I consider to be the most fundamental question of sediment deposition: How does the nature of the deposit depend upon the characteristics of the flow and the nature of the load? If sedimentologists are ever going to be able to make interpretations about depositional conditions by examining the texture of the deposit, they are going to have to answer that question first.
The Active Layer
There is more to the selection process than might seem to you at first thought. First I would like to divide the sediment bed into two depth zones (Figure \(\PageIndex{3}\)). The uppermost zone, extending some distance down from the bed surface, is called the active layer. The sediment in the active layer is subjected to repeated re-entrainment by the flow as the bed elevation at any given point rises and falls as a result of local erosion and deposition that is superimposed on the long-term net deposition. A good example of such temporary changes in bed elevation are those associated with the passage of bed forms. All the sediment within the active layer is recycled by the flow at least once by the flow before it is permanently buried. Below the active layer is the substrate, which might be called the permanent deposit. The sediment in the permanent deposit is below the reach of the local erosional processes of the flow, and it will never again be entrained by the flow unless the overall depositional regime changes into an overall erosional regime at some later time. (You thus have to take the word “permanent” to apply to a time that extends into the future only as far as the flow conditions remain fairly constant.)
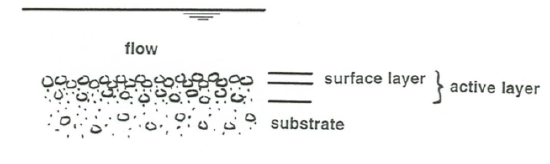
The thickness of the active layer may range from just several grain diameters, on an approximately planar bed undergoing aggradation, to many meters, when the bed is covered with very large bed forms that deposit and re- erode sediment as they move downstream.
When viewed in terms of the active layer, deposition therefore involves the burial of certain particles deeply enough within the active layer so that they are no longer moved by the flow again, whereupon they become part of the permanent deposit. During long-term aggradation at a point on the sediment bed, the active layer rises vertically, relative to some datum buried deeply in the substrate. Sediment particles are added to the active layer from the sediment load, by way of resting at least briefly on the bed surface, and at the same time the base of the active layer rises upward through the deposit, as particles at the base of the active layer pass beyond the reach of the flow (or, in other words, as the probability of eventual re-entrainment by the flow becomes zero).
Fractionation
If we lived in a world of unisize (and “unishape” and “unidensity”) sediment (a boring world, for sedimentationists!), then what has gone before in this section would be all that there is to it. In the real world, however, every sediment contains a range of particle sizes, shapes, and densities, as you have seen earlier in these notes. (Here, for convenience, I will refer to fractions in the three-dimensional joint frequency distribution of size, shape, and density as “SSD fractions”.) This opens up the possibility of fractionation: the spatial segregation of different SSD fractions during transport and deposition.
The simplest kind of fractionation to understand is lateral: different SSD fractions can be deposited, or stored, along the “sides” of the transport path—as, for example, in overbank deposition in a river system. As a consequence, the SSF distribution of the transported sediment, which we might call the “throughput”, evolves in the downstream direction.
Because only a subset of the particles of the load end up becoming part of the permanent deposit, there is the possibility of fractionation of the various SSD fractions between the load and the deposit. Obviously, such fractionation can take place only if there is some range of sizes, shapes, or densities in the load in the first place. But all natural sediments show at least some variation in size and shape.
The fractionation can be viewed as a multi-step process, from the load, to the bed surface, to the active layer, and finally to the permanent deposit. Figure \(\PageIndex{4}\) shows some general things about the course of this fractionation during deposition. The first step is fractionation between the load and the bed surface. As you saw in Chapter 13, most tractional flows the bed surface is coarser than the load, although that effect is most striking at weak transport rates and becomes much less at higher transport rates. The rest of the active layer, below the bed surface, is finer than the bed surface, but it can be either finer or coarser than the load. Although more work needs to be done, it seems clear that in weak flows the active layer as well as the bed surface is coarser than the load, but in strong flows carrying coarse sediment the active layer is actually finer than the load! The relationship between the active layer and the permanent deposit is still not well understood, but it does not represent the major effect in fractionation.
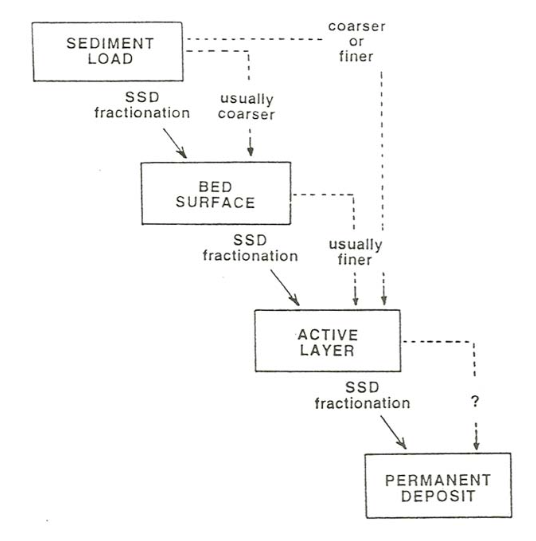
In the strongest flows, with high concentrations of sediment traveling both as bed load and suspended load, the coarser particles less commonly find permanent resting places on the bed, so the deposit is much finer than the load. In weaker flows, on the other hand, under conditions not far above the threshold for particle transport, the mean size of the deposit is greater than the mean size of the load. One’s first reaction is that the stronger the flow, the coarser the deposit. But just the opposite is true! (The qualification here is that we are considering a given supply of sediment that flows with a range of flow strength are constrained to carry.) Here is yet another example of how deduction or intuition can mislead us when it comes to the dynamics of sediment transport by turbulent flows.
A Note on Degradation
Up to now in this chapter the focus has been on aggradation. Degradation is also important to consider, because in a succession of deposited sediment there might be thin intervals that represent periods of temporary degradation, and the nature of the SSD distribution in those intervals can be greatly different from the rest of the succession. In particular, density fractions that are more difficult for the flow to transport might become concentrated to form an economically important placer.
In the context of differential transport (see the earlier section on modes of deposition), if for whatever reason the sediment transport rate increases downstream in a given reach of the flow the bed elevation decreases, causing degradation. If the flow is able to transport all of the sediment that it encounters as it eats into the substrate, then the process can continue indefinitely, for as long as the large-scale changes that cause the degradation—like base-level lowering in a river—continue to operate. If the coarsest of the transported fractions are in the gravel size range, the bed is likely to be paved (see Chapter 13), but the coarser particles that constitute the pavement can be transported by the flow, and so, although the exact nature of the pavement might change with time, degradation can continue. If, however, during degradation the flow encounters size fractions that are so coarse that it cannot transport them, then the pavement evolves into armor, and degradation ceases.


