1.3: Viscosity
- Page ID
- 4150
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Another concept in fluid dynamics, viscosity, is one that is less likely to be within your range of intuition and experience than pressure. Viscosity is a property of fluids that characterizes their resistance to deformation. This section is devoted to making that idea clear to you, and to making a start on exploring its consequences for fluid motions.
Parallel Plate Experiment
For a first look at how fluids behave when they are deformed, here is an experiment you could attempt on your own kitchen table. Arrange two horizontal parallel plates, spaced a distance \(L\) apart, with a fluid at rest between them (Figure \(\PageIndex{1}\)). You could justifiably argue that it would be hard to make such an experiment, because how could you keep the fluid from leaking out at the margins of the plates? Do not worry about such practicalities; just suppose that the plates are very broad relative to their spacing, or that the fluid you have chosen is “thick”, i.e., has a high viscosity (you are likely to have a number of high- viscosity household fluids, like honey, or molasses, or corn syrup, or motor oil, available), which would ooze out from the between the plates only slowly, giving you time to do the experiment described below.
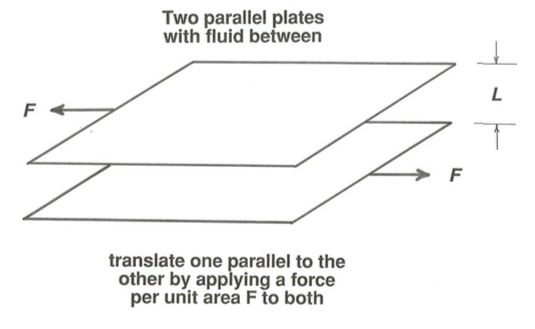
Accelerate the upper plate rapidly to a constant velocity \(V\) parallel to itself by applying a force per unit area, call it \(F\), over its entire surface, while you hold the lower plate fixed by applying to it an equal and opposite force per unit area. You could do that by taping the lower plate to the table and attaching handles with suction cups to the top of the upper plate. The fluid is set in motion by friction from the moving plate.
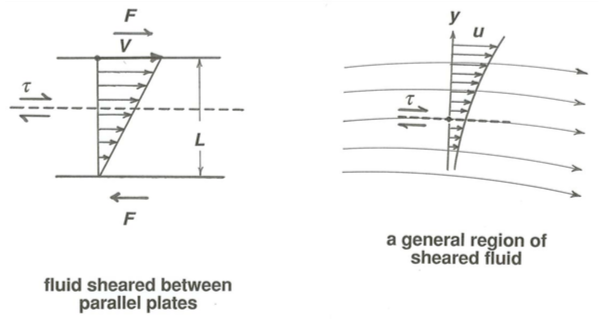
How does the fluid move? You might picture the motion as a series of tabular layers of fluid, parallel to the bounding plates, sliding past one another in a shearing motion, but of course in reality the shearing is continuous rather than as discrete layers. Shear of this kind always acts whenever fluids are in motion relative to solid boundaries—which is just about all the flows we will consider in these notes. If you were somehow able to measure the velocity of the fluid at a large number of points along some imaginary line normal to the plates (Figure \(\PageIndex{2}\)), what would be the distribution of velocity? You would find that after an initial transient period of adjustment during which progressively lower layers of the fluid are brought into motion, the velocity would vary linearly from zero at the stationary plate to \(V\) at the moving plate.
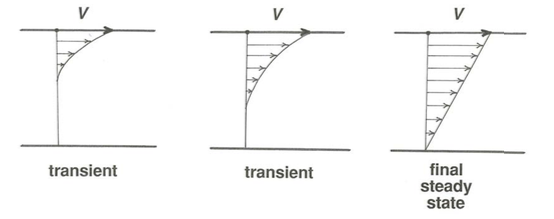
From Figure \(\PageIndex{2}\) you can see that the fluid in contact with each of the plates has exactly the same velocity as the plates themselves. This is a manifestation of what is known as the no-slip condition: fluid in contact with a solid boundary has exactly the same velocity as that boundary. Although this no- slip condition might seem counterintuitive to you, it is a fact of observation, and it can be justified by considerations on intermolecular forces. The flow of the continuously deforming fluid past the solid boundary is not the same as sliding a rigid slab, like a brick, across a table top. Intermolecular forces act between the fluid and the solid at the boundary just as they do across planes of shearing in the interior of the fluid, so there’s no more reason to expect a discontinuity in velocity at the boundary than within the fluid.
Shear Stress
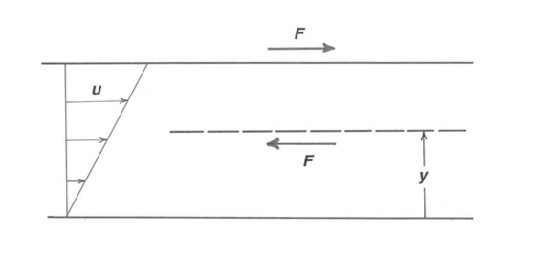
To see why the velocity distribution between the plates is linear, pass an imaginary plane, parallel to the plates, anywhere through the fluid (Figure \(\PageIndex{3}\)). Because the fluid contained between this plane and either the lower plate or the upper plate is not being accelerated after the steady state is attained, the fluid on either side of this plane must be exerting on the fluid on the other side of the plane the same force per unit area \(F\) as that on the plates themselves. Because the imaginary plane can be located anywhere between the two plates, the shearing force per unit area across all such planes in the fluid, called the shear stress, must be the same. (From here on, keep firmly in mind the distinction between shear, an aspect of the geometry of fluid deformation, and shear stress, the shearing force per unit area associated with the shearing.) And because the fluid must be expected to shear or deform at the same rate for the same applied shearing force, the rate of change of velocity normal to the plates must be constant: assuming the \(y\) axis to be normal to the plates, and letting \(u\) be the velocity of the fluid at a point,
\[d u / d y=k \label{dudy} \]
where \(k\) is some constant. So the velocity itself must vary linearly: taking \(y=0\) at the lower plate,
\[u=\int k d y=k y+c\]
Evaluating the constant of integration \(c\) by using the no-slip condition that \(u = 0\) at \(y = 0\), we find \(c = 0\), so
\[u=k y \label{uky} \]
For more on what determines the magnitude of that constant \(k\), see a later paragraph.
Viscosity
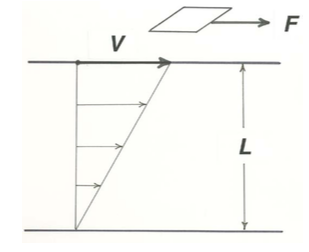
What determines the value of \(F\) needed to produce a given difference in velocity between the two plates (Figure \(\PageIndex{4}\))? For many fluids the ratio of \(F\) to the quantity \(V/L\), which represents the rate of shear in the fluid, would be found to be the same for all values of \(F\):
\[F /(V / L)= \mathrm{const, or } F=\mathrm{const} \cdot(V / L) \label{ratio} \]
This constant ratio, the ratio of applied shear stress to the resulting rate of shear, usually denoted by \(\mu\), is called the viscosity of the fluid. The viscosity is this the fluid property that characterizes the resistance of the fluid to deformation. For fluids like air and water, the viscosity is indeed an intrinsic property of the fluid, in that it does not depend on the state of motion but only on the nature of the fluid itself. Different fluids have different viscosities. Fluids with higher viscosities require a greater shearing force per unit area to produce a given rate of shearing, and fluids with higher viscosities have a greater rate of shearing for a given shearing force per unit area. For a given fluid the viscosity is a function of temperature; for water, viscosity decreases with temperature, but for air, viscosity increases with temperature.
Universal Case
Now we need to generalize beyond the kitchen-table experiment. Here comes a substantial conceptual jump. The parallel-plate experiment is a rather specialized case of shearing in a fluid. In a more general flow, the geometry of the flow is more complicated and the rate of shear and the corresponding shearing force per unit area generally varies from place to place. Even so, the deformation of the fluid in any tiny volume can be visualized in the same way as in the parallel-plate experiment. A relationship like Equation \ref{ratio} holds at every point in a sheared fluid, no matter how much the rate and orientation of the shearing vary from place to place:
\[\frac{\tau}{d u / d y}=\mu\]
or
\[\tau=\mu \frac{d u}{d y} \label{shearstress} \]
where \(\tau\) is the shear stress (i.e., the local shearing force per unit area) exerted across the shearing surfaces at some point in the fluid, and \(d u / d y\) is the rate of change of the local fluid velocity \(u\) in the direction \(y\) normal to the shearing surfaces at the point (Figure \(\PageIndex{5}\)). We will often have occasion to make use of Equation \ref{shearstress} later in the course. I have sidestepped its derivation from first principles; that would necessitate starting from Newton’s second law, written in differential form, for the general fluid motion. I hope that the shortcut I have presented here gives you a good understanding of the significance of Equation \ref{shearstress}.
You can see now the significance of \(k\) in the linear velocity distribution in Equation \ref{uky} for shearing of a fluid between parallel plates. Combine Equation \ref{shearstress}, the general relationship between shear stress and shear rate, with the result, found above for the parallel-plate experiment, that \(d u / d y = k\) (Equation \ref{dudy}), which expresses that the spatial rate of change, in the direction normal to the planes of shearing, of local fluid velocity is the same at all levels between the plates:
\[\frac{d u}{d y}=k=\frac{\tau}{\mu} \label{1.9} \]
So the constant \(k\) reflects the relative magnitude of the applied shearing force per unit area and the viscosity: for given viscosity, a greater applied shearing force per unit area on the upper plate produces a steeper velocity gradient in the fluid, and for given applied force per unit area, a given viscosity produces a less steep velocity gradient.
Why do fluids resist deformation? The shear stress that is mutually exerted across the surfaces of shear in the fluid, like the shear planes in the fluid between the parallel plates on your kitchen table, can be thought of as internal friction. For liquids, to account for the origin of this internal friction you can appeal to the necessity of stretching and breaking the fleeting bonds between the adjacent close-lying molecules of the fluid whose centers lie on one side or other of the imaginary shear plane. For gases, however, the picture is not as straightforward (although ultimately simpler mechanically!) because gases consist of isolated atoms or molecules pursuing their free paths and interacting among themselves only relatively infrequently. In gases, the shear planes pass through mostly empty space, and the constituent particles are for the most part moving freely as they pass across the shear planes in one direction or the other. To present a satisfactory account of the origin of internal friction in sheared gases, we have to deal with the phenomenon of diffusion. Diffusion is an important physical process that will figure in a number of later topics in these notes as well, so this is a good place, in the following section, to address it.


