9.6.1: Complex geometry of tidal basins
- Page ID
- 16407
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The interaction between bottom morphology and tidal motion is the cause of a complex three-dimensional structure of residual circulations, which are both the cause and the result of the morphology of the basins. The residual circulations in meandering channels play an active role in the morphological evolution of channel meanders and of ebb and flood chutes, as will be described below. Sedimentation, erosion and sand and marsh flats are connected with these flow structures.
Section 5.7.6 described the transversal secondary flow induced by the curvature of the tidal current in channel bends and by the Coriolis effect. This secondary flow, though rather weak compared to the maximum tidal current, can have a significant residual effect on the current, and also on the sediment transport and the bed topography. The curvature-induced secondary flow does not change sign as the tide turns: in the upper part of the water column it is always directed away from centre of curvature of the flow, in the lower part always towards. This means that near the bottom the secondary flow is towards the inner bend generating a transport of sediment from the outer bend, which erodes, towards the inner bend, which accretes. Hence, this phenomenon has a positive feedback mechanism (see Sect. 1.5.2). Straight channels are inherently unstable; a small eccentricity in the channel alignment will be inclined to grow. Similarly, curvature-induced secondary flow components contribute to the maintenance of shoals, see Fig. 9.13. Note that Coriolis (as well as density gradients) may substantially alter this simple picture.
As a result of Coriolis, amongst others factors, channels will be inclined to split up in an ebb-dominated and a flood-dominated channel. In areas where the width of the basin is not restricted, two mainly independent channel systems can develop; the ebb current concentrates in one set of channels while the flood current is often strongest in a different set of channels. Flood channels can usually be recognised because they tend to be shallower than ebb channels and they tend to die out; they lead to progressively shallower water and finally spread out on a shoal. Conversely ebb channels are continuous and tend to be deeper. Often the maximum ebb current occurs when the tide level is lower than that corresponding to the maximum flood current (for a velocity leading the surface elevation by less than 90°, see Sect. 5.7.3). Further, in the case of a river discharge, the total discharge during ebb is larger than during flood. The combined effect of higher total ebb flow and the lower tidal level during this flow tends to increase the velocity and enhances erosion in ebb channels.
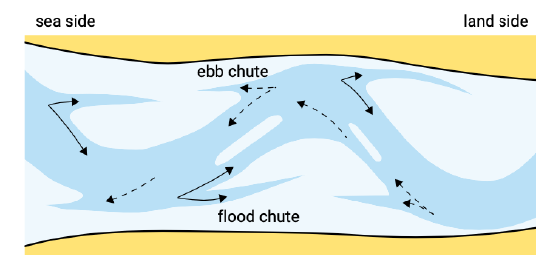
Due to inertia, the tidal current is inclined to go off (overshoot) the bend pathway (or take a wider bend; in Dutch: ‘uit de bocht schieten’), both during ebb and flood. Since the currents try to take a wider bend, ebb and flood chutes occur at the ending of the bends and are directed into the flat areas. Due to the fact that the mean water level during flood (especially near the ending of the flood) is higher than during ebb, the flood chutes are generally better developed than the ebb chutes. During the flood tide, the water spreads over the flats, while the ebb current primarily follows the main channel. Figure 9.24 sketches the characteristic structure of ebb and flood channels in a meandering channel system, with an indication of the depth-mean residual flow pattern.
The flats are especially fed with sand through the ebb and flood chutes. This feeding process causes the existence of sills between the ebb and flood chutes. When a sill breaches, the channel bend is cut-off. A new, straighter channel is formed, while the old main channel accretes. However, in the course of time the new channel will start to increase its curvature. Hence, the morphology of tidal basins is not static but dynamic; cycles of increasing channel curvature and channel cut-off are an important part of these internal dynamics.


