22.2: Liquid-Drop Optics
- Page ID
- 10195
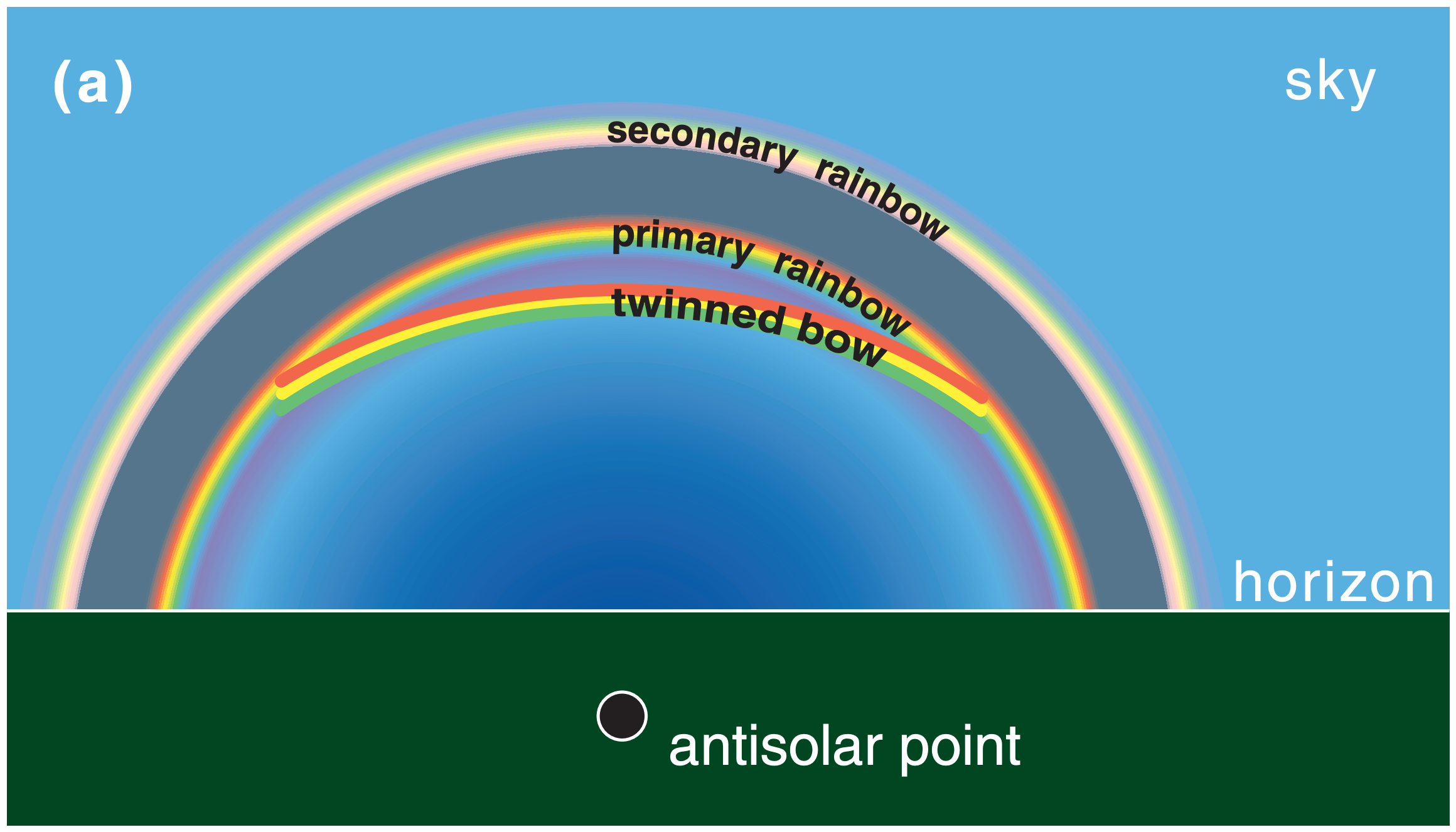
Most raindrop water optics are found by looking away from the sun. Rainbows are circles or portions of circles (Fig. 22.6) that are centered on the antisolar point, which is the point corresponding to the shadow of your head or camera. (As viewed by the observer, the antisolar point is also called the sun’s antipodal point.)

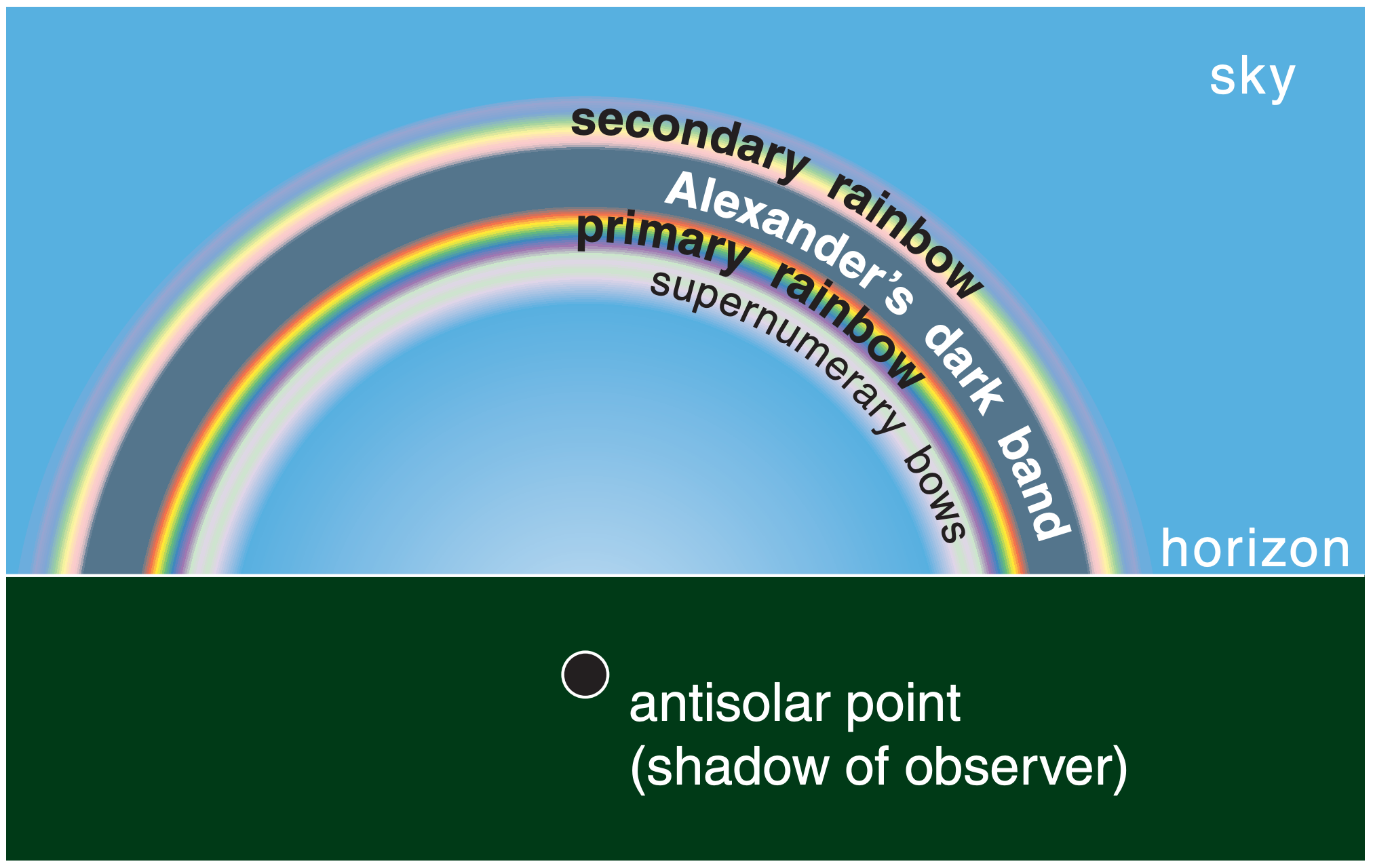
Primary rainbows have red on the outside of the circle, and are the brightest and most easily seen (Fig. 22.7). The viewing angle (θview = angle between two lines: the line from your eye to the rainbow and the line from your eye to the antisolar point) is about 42°. Secondary rainbows have red on the inside at viewing angle of about 50°. Supernumerary bows are very faint, and touch the inside of the primary rainbow — these will be discussed in the Diffraction and Interference section.
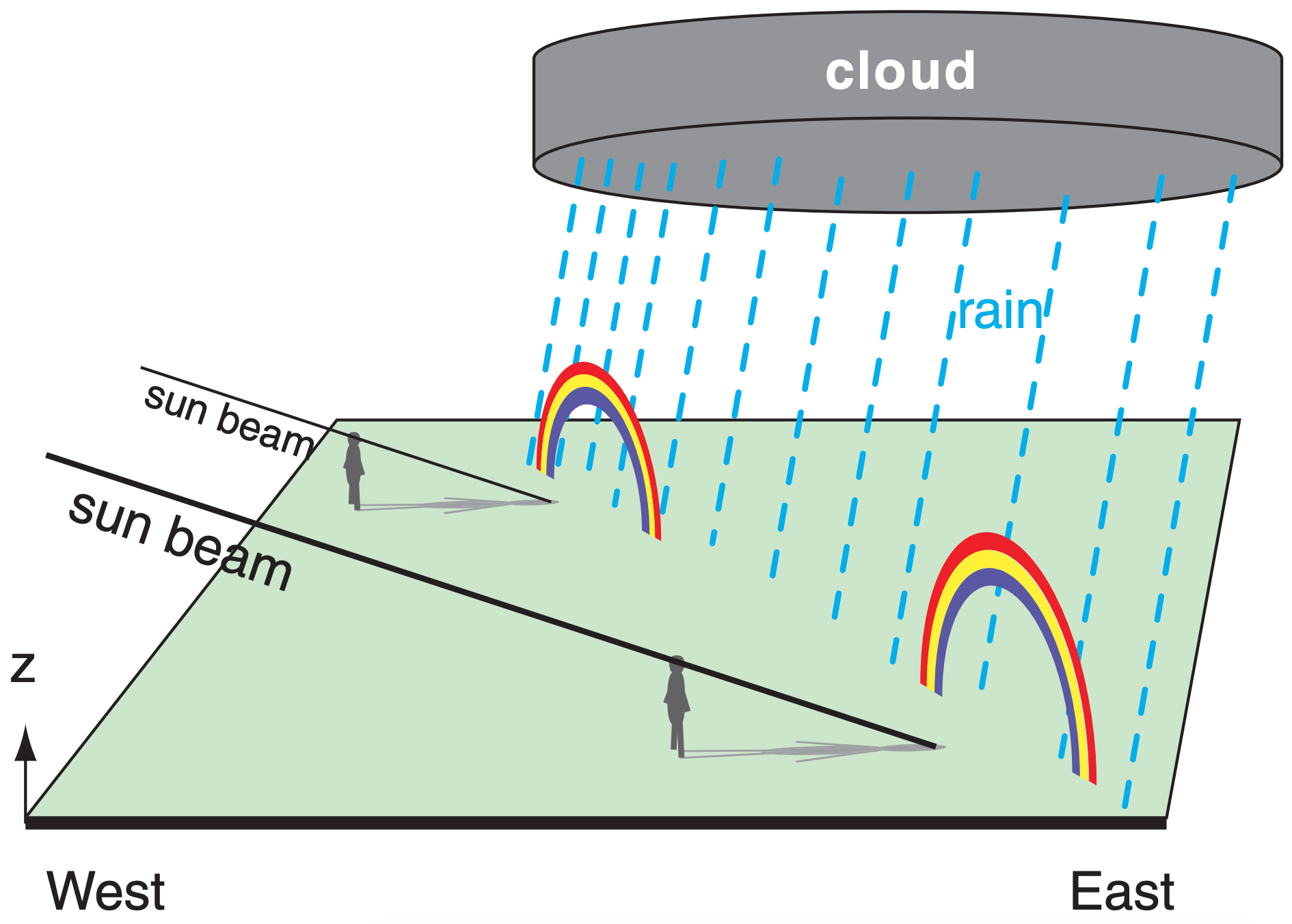
At any one time for any one rain storm, different observers see different rainbows caused by different light rays interacting with different raindrops (Fig. 22.8). Hence, one observer in a region of bright sun and large drops might see a vivid rainbow, while another observer a half kilometer away might see only a weak or partial rainbow in light rain with smaller drops.
We can explain these rainbow phenomena using geometric optics, assuming spherical raindrops. First, we will consider the portion of incident sunlight that is lost due to reflection off the outside of the drop. Then we will look at the remainder that is refracted and reflected in the drop to make the rainbow.
22.2.1. Reflection from Water
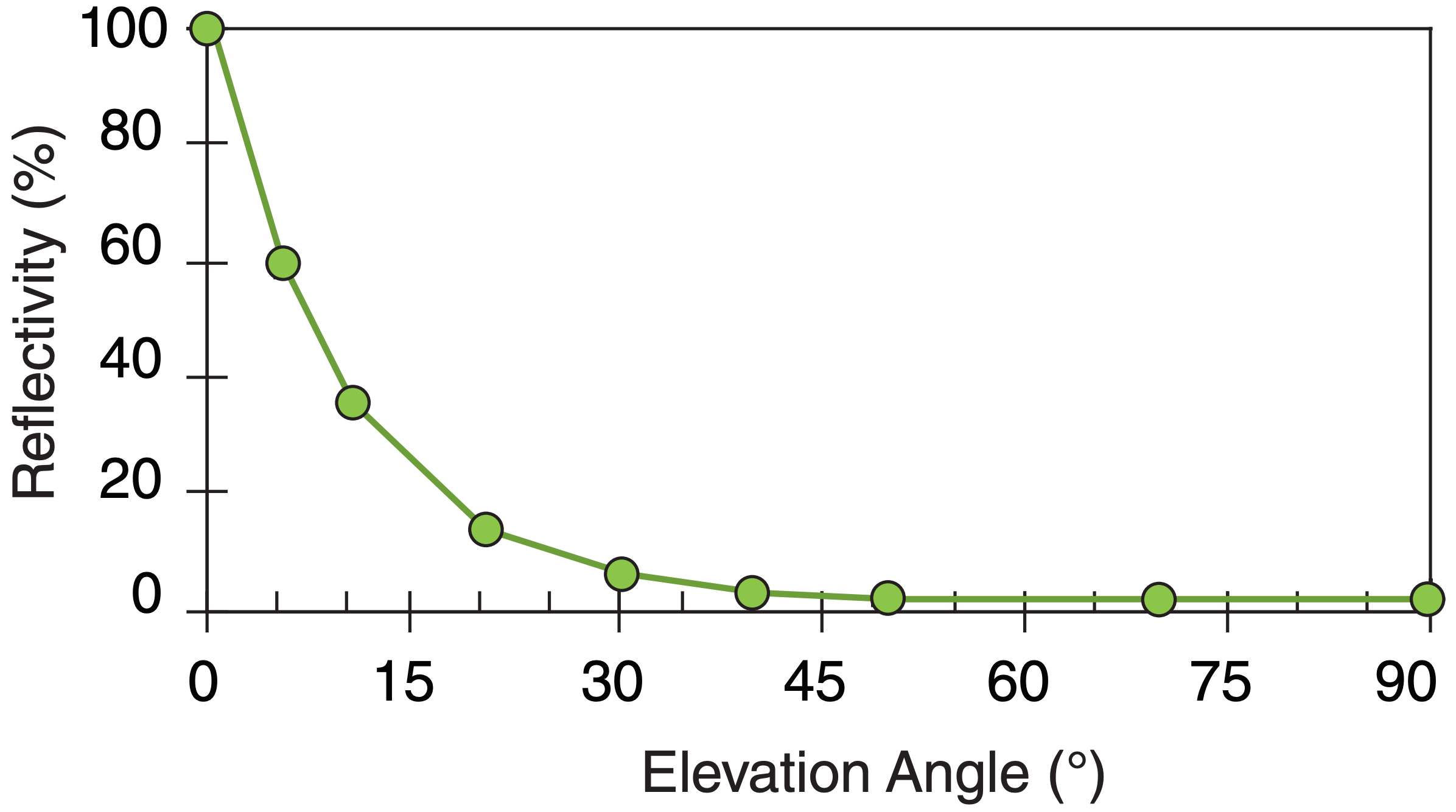
Rays of light that hit a water surface at a shallow angle are reflected more than those hitting straight on. Reflectivity r vs. elevation angle Ψ above the water surface is approximately:
\begin{align}r=r_{o}+r_{1} \cdot \mathbf{e}^{-\Psi / a}\tag{22.11}\end{align}
where ro = 0.02, r1 = 0.98, and a = 9.3°. This is plotted in Fig. 22.9.
Sample Application
Just after sunrise, sunlight hits a smooth lake surface at elevation angle 5°. Find the reflectivity.
Find the Answer
Given: Ψ = 5°
Find: r = ? (dimensionless
Use eq. (22.11): r = 0.02 + 0.98·exp(– 5°/9.3°) = 0.59
Check: Units dimensionless. Magnitude agrees with Fig. 22.9.
Exposition: 59% of incident sunshine in this case is reflected away, and is not available to heat the lake.
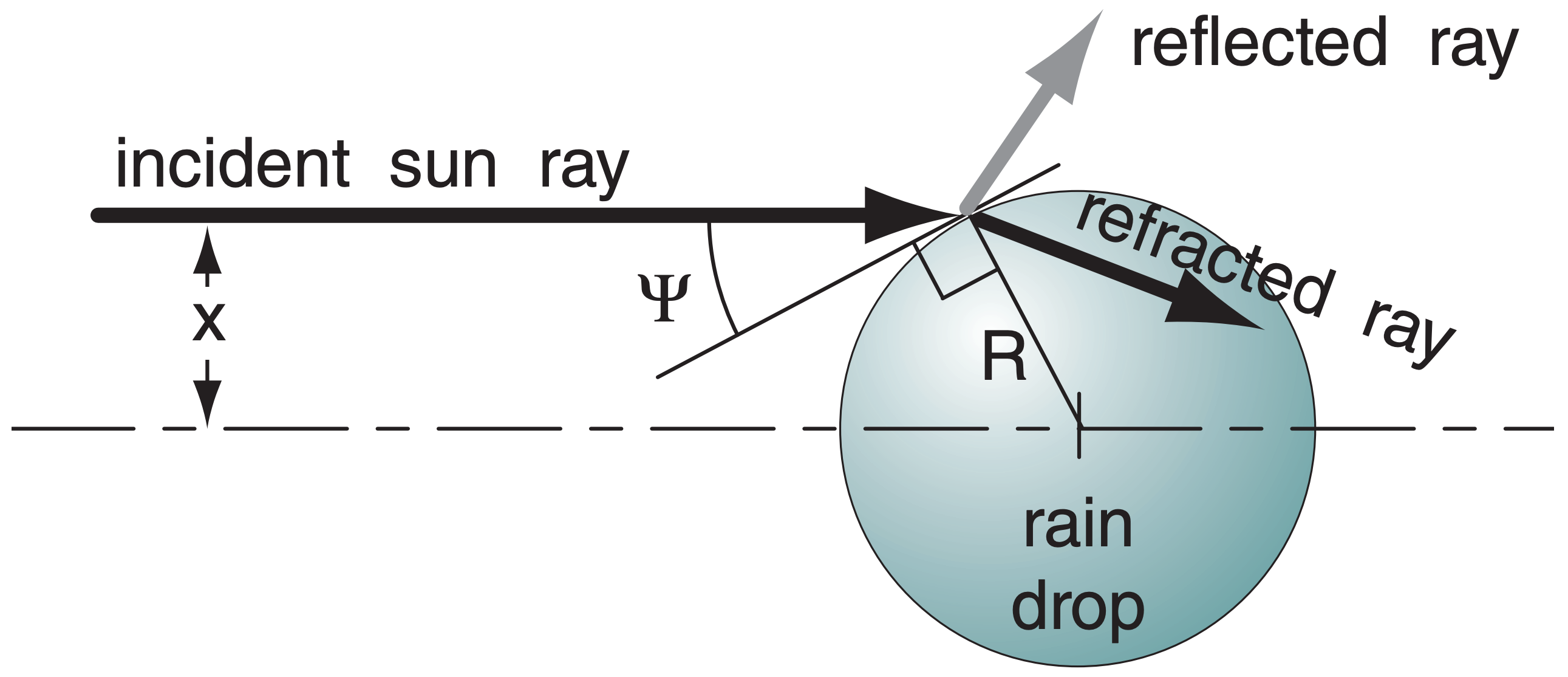
Rays of sunlight can enter a spherical drop at any distance x from the centerline (Fig. 22.10). The ratio of this distance to the drop radius R is called the impact parameter (x/R). Because of curvature of the drop surface, rays arriving at larger impact parameters strike the drop at smaller elevation angles:
\begin{align}\psi=\arccos \left(\frac{x}{R}\right)\tag{22.12}\end{align}
Thus, the amount of reflected light from a drop increases with increasing impact parameter.
22.2.2. Primary Rainbow
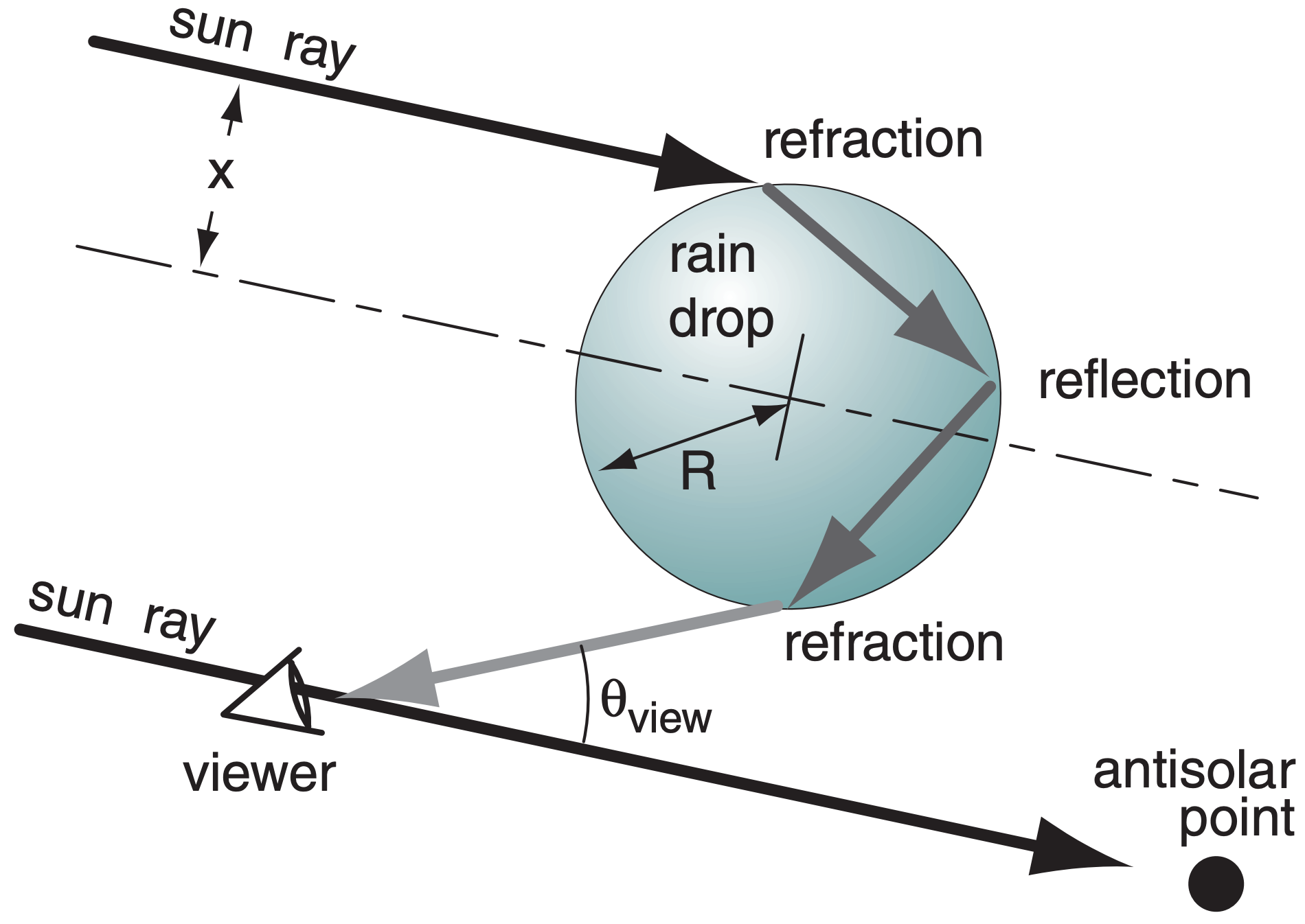
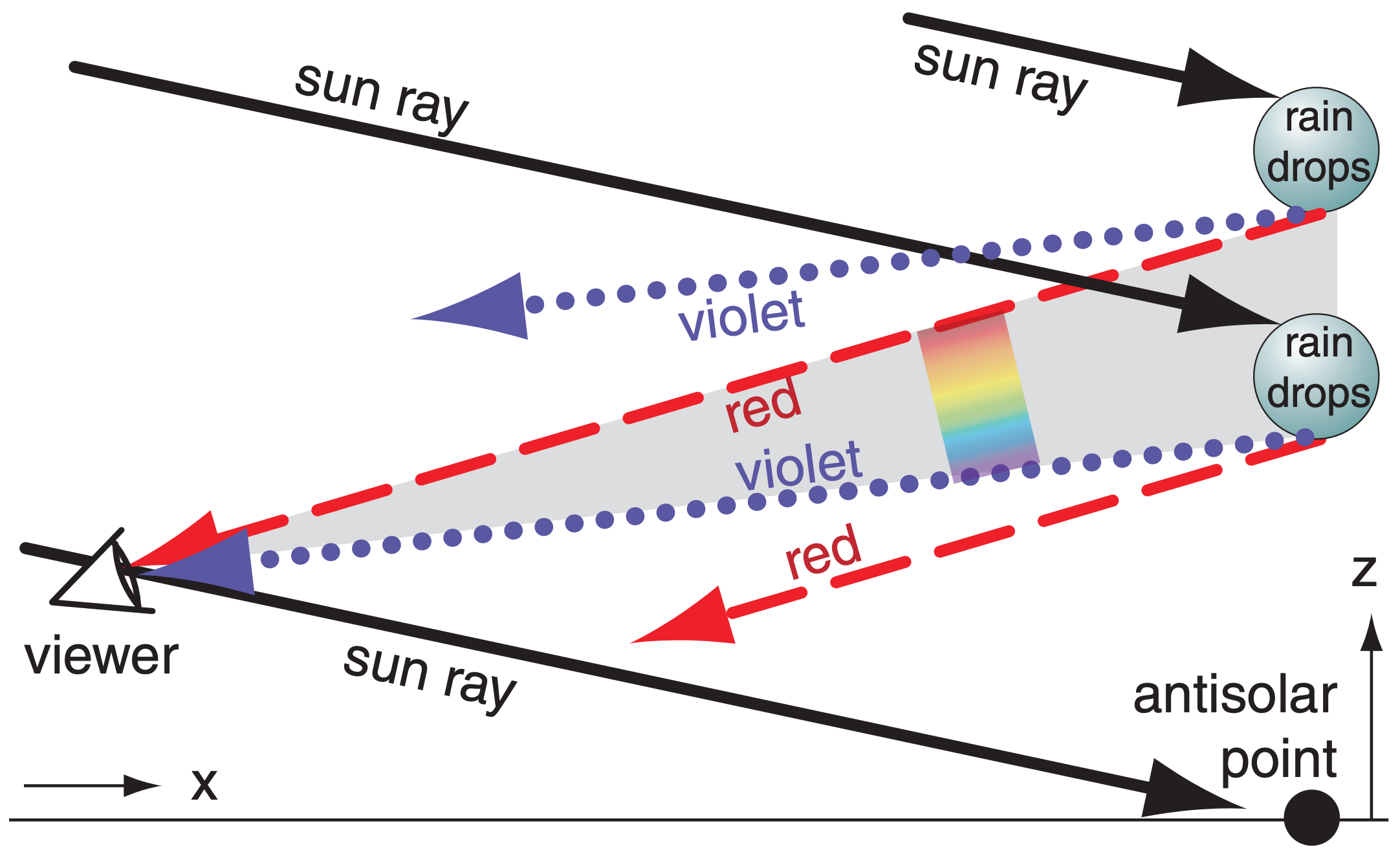
Rays that are not reflected from the outside of the drop can make zero or more reflections inside the drop before leaving. Those entering rays that make one reflection (in addition to the two refractions during entry and exit) cause the primary rainbow (Fig. 22.11). White light is dispersed by the refractions such that reds are bent less and appear on the outside of the rainbow circle, because they come to your eyes from raindrops further from the antisolar point. Violets are bent more and appear on the inside (Fig. 22.12) because the come to your eyes from other drops that are closer to the antisolar point.
Variations of impact parameter cause a range of output viewing angles θview according to:
\begin{align}\theta_{\text {view}}=4 \cdot \arcsin \left(\frac{n_{\text {air}}}{n_{\text {water}}} \cdot \frac{x}{R}\right)-2 \cdot \arcsin \left(\frac{x}{R}\right)\tag{22.13}\end{align}
where x/R is the impact parameter, and n is refractive index. In other words, there is not a single magic angle of 42° for the primary rainbow. Instead, there is a superposition of many rays of different colors with a wide range of viewing angles.
To learn how these rays interact to form the rainbow, we can solve eq. (22.13) on a spreadsheet for a large number of evenly spaced values of the impact parameter, such as intervals of 0.02 for x/R. Output viewing angles, measured from the antisolar point, range between 0° and 42.7°, as plotted in Fig. 22.13a. This is why the sky is brighter inside the primary rainbow (i.e., for viewing angles of 0 to 42.7°), than just outside of it.
Sample Application
For red light calculate the primary-rainbow viewing angle for x/R= 0.70 in air of P= 80 kPa and T= 0°C.
Find the Answer
Given: x/R = 0.70 nair = 1.0002295, nwater = 1.3315 from Table 22-1.
Find: θview = ?°
Use eq. (22.13) for the primary rainbow:
Check: Units OK. Physics OK. Agrees with Fig. 22.13.
Exposition: This lights inside the primary rainbow.
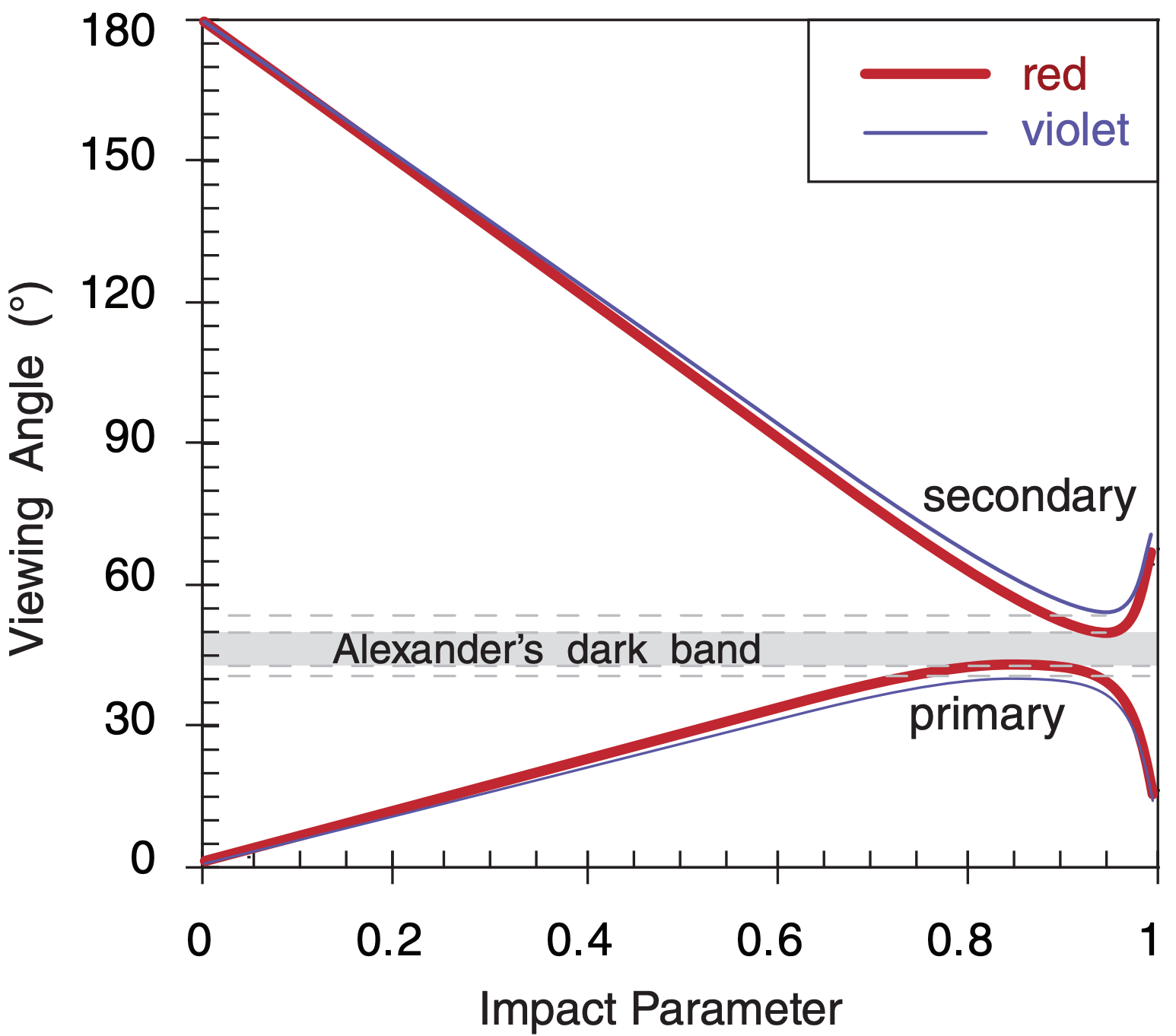
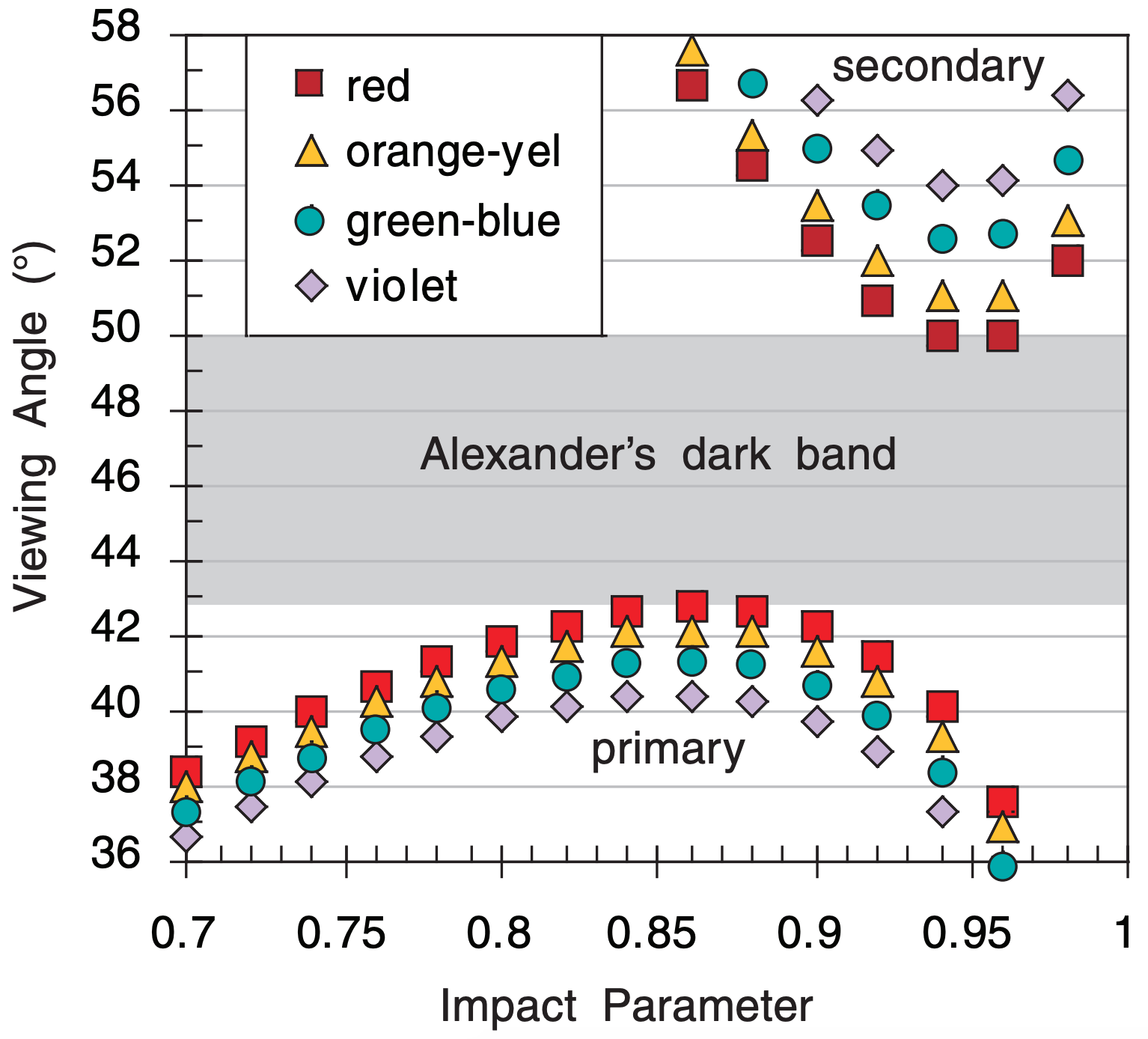
Fig. 22.13b is a blow-up of Fig. 22.13a. Three of the data points have a viewing angle of about 42.5°, and these all correspond to rays of red light. Hence, the primary rainbow looks red at that viewing angle. At 42.0°, there are mostly orange-yellow data points, and just a couple red points. Hence, at this angle the rainbow looks orange. Similar arguments explain the other colors. Inside the primary rainbow the sky looks white, because roughly equal amounts of all colors are returned at each viewing angle.
22.2.3. Secondary Rainbow
Entering light rays can also make two reflections before leaving the raindrop, as sketched in Fig. 22.14. The extra reflection reverses the colors, putting red on the inside of the circle of a secondary rainbow. At each internal reflection some light is lost (refracted) out of the drop. Thus, the secondary rainbow is faint — only 43% as bright as the primary rainbow.
The relationship between impact parameter and viewing angle for a secondary rainbow is:
\begin{align}\theta_{\text {view}}=180^{\circ}+2 \cdot \arcsin \left(\frac{x}{R}\right)-6 \cdot \arcsin \left(\frac{n_{\text {air}}}{n_{\text {water}}} \cdot \frac{x}{R}\right)\tag{22.14}\end{align}
where x/R is the impact parameter, and n is refractive index. Again, a range of output viewing angles occurs because light enters over the full range of impact parameters. In this case, the sky is dark inside of the secondary rainbow (about 50° viewing angle), and bright outside, as sketched in Figs. 22.13a & b, based on spreadsheet calculations.
Higher-order rainbows (having more internal reflections) are theoretically possible, but are rarely seen because they are so faint:
- 3 internal reflections
θview = 137.52°
intensity ≈ 24% as bright as the primary
- 4 internal reflections
θview = 137.24°
intensity ≈ 15% as bright as the primary
- 5 internal reflections
θview = 52.9°
very faint
Viewing angles for tertiary and quaternary rainbows are 43° from the sun (i.e., not from the antisolar point). Hence, their faint presence is washed out by the intense zero-order glow from the sun. Zero-order glow is light from the sun passing through a raindrop with no internal reflections while en route to the observer.
German monk Theodoric von Freiberg created a physical model of rainbow physics in 1304 by filling a glass sphere with water. By carefully shining light through it at different impact parameter values, he could measure the various output angles. However, the physics behind these observations were not explained until the renaissance, after Willebrod Snell van Royen had discovered the law for refraction in the early 1600’s.
Twenty years after Snell’s discovery, Descartes used it to demonstrate the capabilities of his scientific method by mathematically solving the rainbow problem. His calculations were very similar to our spreadsheet calculations, except that he manually performed calculations for a large number of different impact parameters. Through these repetitive “brute-force” calculations he verified the magic number of 42° for the brightest returned light, and 50° for the secondary rainbow.
About 30 years later, Newton applied his knowledge of color dispersion to explain why the rainbow has colors. Also, he was able to use his invention of calculus to elegantly derive the magic angle of 42°.
22.2.4. Alexander’s Dark Band
Neither the primary nor secondary rainbows return light in the viewing-angle range between 42.7° and 50°. Hence, the sky is noticeably darker between these rainbows (Figs. 22.7 & 22.13). This dark region is called Alexander’s dark band, after Greek philosopher Alexander of Aphrodisias who described it during the third century A.D.
22.2.5. Other Rainbow Phenomena
Larger-diameter raindrops cause more vivid, colorful rainbows. But as discussed in the Satellite & Radar chapter, large raindrops are often not spherical. A mixture of large non-spherical drops (oblate spheroids the shape of hamburger buns) and moderate-sized spherical drops causes cause twinned rainbows, where the top of the rainbow circle splits into two rainbows (Fig. 22.15a).
Sea-spray rainbows are about 0.8° smaller radius than normal rainbows, because of greater refraction by salt water. Near sunset, the blue-diminished sunlight illuminates raindrops with reddish light, creating red bows with enhanced red and orange bands. Faint rainbows (moon bows) can also be created by moonlight at night.
Reflection rainbows form when the incident sunlight bounces off a lake before hitting the raindrops (Fig. 22.15b). This bow is centered on the anthelic point, which is as high above the horizon as the antisolar point is below, but at the same azimuth.