18.6: Turbulence
- Page ID
- 9649
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)18.6.1. Mean and Turbulent Parts
Wind can be quite variable. The total wind speed is the superposition of three types of flow:
- mean wind – relatively constant, but varying slowly over the course of hours;
- waves – regular (linear) oscillations of wind, often with periods of ten minutes or longer;
- turbulence – irregular, quasi-random, non- linear variations or gusts, with durations of seconds to minutes.
These flows can occur individually, or in any combination. Waves are discussed in the Regional Winds chapter. Here, we focus on mean wind and turbulence.
Figure 18.23 The instantaneous wind speed U is shown by the zigzag line. The average wind speed \(\ \bar{U}\) is shown by the thin green horizontal dashed line. A gust velocity u’ is the instantaneous deviation of the instantaneous wind from the average.

Let U(t) be the x-direction component of wind at some instant in time, t. Different values of U(t) can occur at different times, if the wind is variable. By averaging the instantaneous wind measurements over a time period, P, we can define a mean wind \(\ \overline{U}\), where the overbar denotes an average. This mean wind can be subtracted from the instantaneous wind to give the turbulence or gust part u’ (Fig. 18.23). Thus, the wind can be considered as a sum of mean and turbulent parts (neglecting waves for now).
Similar definitions exist for the other wind components (U, V, W), temperature (T) and humidity (r):
\( \begin{align}u^{\prime}(t)=U(t)-\bar{U}\tag{18.20a}\end{align}\)
\(\ \begin{align}v^{\prime}(t)=V(t)-\bar{V}\tag{18.20b}\end{align}\)
\(\ \begin{align}w^{\prime}(t)=W(t)-\bar{W}\tag{18.20c}\end{align}\)
\(\ \begin{align}T^{\prime}(t)=T(t)-\bar{T}e\tag{18.20d}\end{align}\)
\(\ \begin{align}r^{\prime}(t)=r(t)-\bar{r}\tag{18.20e}\end{align}\)
The averages in eq. (18.20) are defined over time or over horizontal distance. For example, the mean temperature is the sum of all individual temperature measurements, divided by the total number N of data points:
\(\ \begin{align}\bar{T}=\frac{1}{N} \sum_{k=1}^{N} T_{k}\tag{18.21}\end{align}\)
where k is the data-point index (corresponding to different times or locations). The averaging time in eq. (18.21) is typically about 0.5 h. If you average over space, typical averaging distance is 50 to 100 km.
Sample Application
Given the following measurements of total instantaneous temperature, T, find the average \(\ \bar{T}\). Also, find the T`values.
| t (min) | T (°C) | t (min) | T (°C) |
| 1 | 12 | 6 | 13 |
| 2 | 14 | 7 | 10 |
| 3 | 10 | 8 | 11 |
| 4 | 15 | 9 | 9 |
| 5 | 16 | 10 | 10 |
Find the Answer
As specified by eq. (18.21), adding the ten temperature values and dividing by ten gives the average \(\ \bar{T}\) = 12.0°C. Subtracting this average from each instantaneous temperature gives:
| t (min) | T ‘(°C) | t (min) | T ‘(°C) |
| 1 | 0 | 6 | 1 |
| 2 | 2 | 7 | –2 |
| 3 | –2 | 8 | –1 |
| 4 | 3 | 9 | –3 |
| 5 | 4 | 10 | –2 |
Check: The average of these T’ values should be zero, by definition, useful for checking for mistakes.
Exposition: If a positive T’ corresponds to a positive w’, then warm air is moving up. This contributes positively to the heat flux.
Short term fluctuations (described by the primed quantities) are associated with small-scale swirls of motion called eddies. The superposition of many such eddies of many sizes makes up the turbulence that is embedded in the mean flow.
Molecular viscosity in the air causes friction between the eddies, tending to reduce the turbulence intensity. Thus, turbulence is NOT a conserved quantity, but is dissipative. Turbulence decays and disappears unless there are active processes to generate it. Two such production processes are convection, associated with warm air rising and cool air sinking, and wind shear, the change of wind speed or direction with height.
Normally, weather forecasts are made for mean conditions, not turbulence. Nevertheless, the net effects of turbulence on mean flow must be included. Idealized average turbulence effects are given in the chapters on Thermodynamics, Water Vapor, and Atmos. Forces and Winds.
Meteorologists use statistics to quantify the net effect of turbulence. Some statistics are described next. In this chapter we will continue to use the overbar to denote the mean conditions. However, we drop the overbar in most other chapters in this book to simplify the notation.
18.6.2. Variance and Standard Deviation
The variance σ2 of wind speed is an overall statistic of gustiness. For example, for vertical velocity:
\(\ \begin{align}\begin{aligned}
\sigma_{w}^{2} &=\frac{1}{N} \sum_{k=1}^{N}\left(W_{k}-\bar{W}\right)^{2} \\
&=\frac{1}{N} \sum_{k=1}^{N}\left(w_{k}^{\prime}\right)^{2} \\
&=\frac{w^{\prime} 2}{w^{\prime}}
\end{aligned}\tag{18.22}\end{align}\)
Similar definitions can be made for σu2 , σv2 , σθ2 , etc. Statistically, these are called “biased” variances. Velocity variances can exist in all three directions, even if there is a mean wind in only one direction.
The standard deviation σ is defined as the square-root of the variance, and can be interpreted as an average gust (for velocity), or an average turbulent perturbation (for temperatures and humidities, etc.). For example, standard deviations for vertical velocity, σw, and potential temperature, σθ , are:
\(\ \begin{align}\sigma_{w}=\sqrt{\sigma_{w}^{2}}=(\overline{\left.w^{\prime}\right)^{2}}^{1/2}\tag{18.23a}\end{align}\)
\(\ \begin{align}\sigma_{\theta}=\sqrt{\sigma_{\theta}^{2}}=\overline{\left(\theta^{\prime}\right)^{2}}^{1 / 2}\tag{18.23b}\end{align}\)
Larger variance or standard deviation of velocity means more intense turbulence.
Sample Application (§)
(a) Given the following V-wind measurements.
Find the mean wind speed, and standard deviation.
(b) If the standard deviation of vertical velocity is 1 m s–1, is the flow isotropic?
| t (h) | V (m s–1) |
| 0.1 | 2 |
| 0.2 | –1 |
| 0.3 | 1 |
| 0.4 | 1 |
| 0.5 | –3 |
| 0.6 | –2 |
| 0.7 | 0 |
| 0.8 | 2 |
| 0.9 | –1 |
| 1.0 | 1 |
Find the Answer
Given: Velocities listed at right
σw = 1 ms–1.
Find: \(\ \bar{V}\) = ? m s–1, σv = ? m s–1, isotropy = ?
(a) Use eq. (18.21), except for V instead of T:
\(\ \bar{V}(z)=\frac{1}{n} \sum_{i=1}^{n} V_{i}(z)=\frac{1}{10}(0)=\underline{\bf{0ms^{-1}}}\)
Use eq. (18.22), but for V:
\(\ \sigma_{v}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(V_{i}-\bar{V}\right)^{2}\)
σv2 =(1/10)·(4+1+1+1+9+4+0+4+1+1) = 2.6 m2s–2
Finally, use eq. (18.23), but for v:
\(\\sigma_{v}=\sqrt{2.6 m^{2} \cdot s^{-2}}=\underline{\mathbf{1 .61ms^{-1}}}\)
Check: Units OK. Physics OK.
Exposition: (b) Anisotropic, because σv > σw (see next subsection). This means that an initially spherical smoke puff would become elliptical in cross section as it disperses more in the horizontal than the vertical.
For statically stable air, standard deviations in an ABL of depth h have been empirically found to vary with height z as:
\(\ \begin{align} \sigma_{u}=2.2 \cdot u_{*} \cdot[1-(z / h)]^{3 / 4}\tag{18.24a}\end{align}\)
\(\ \begin{align}\sigma_{v}=2.2 \cdot u_{*} \cdot[1-(z / h)]^{3 / 4}\tag{18.24b}\end{align}\)
\(\ \begin{align}\sigma_{w}=1.73 \cdot u_{*} \cdot[1-(z / h)]^{3 / 4}\tag{18.24c}\end{align}\)
where u* is friction velocity. These equations work when the stability is weak enough that turbulence is not suppressed altogether.
For statically neutral air:
\(\ \begin{align}\sigma_{u}=2.5 \cdot u_{*} \cdot \exp (-1.5 \cdot z / h)\tag{18.25a}\end{align}\)
\(\ \begin{align}\sigma_{v}=1.6 \cdot u_{*} \cdot[1-0.5 \cdot(z / h)]\tag{18.25b}\end{align}\)
\(\ \begin{align}\sigma_{w}=1.25 \cdot u_{*} \cdot[1-0.5 \cdot(z / h)]\tag{18.25c}\end{align}\)
Sample Application (§)
Plot the vertical profiles of standard deviation of vertical velocity for statically stable and neutral situations for which the friction velocity is 0.5 m s–1. The boundary-layer depth is 300 m.
Find the Answer
Given: u* = 0.5 m s–1, h = 300 m
Find: σw = ? vs. z for neutral and stable conditions
Use eqs. (18.24c and 18.25c). For example, for z = 100m:
Stable:
σw = 1.73·(0.5m s–1)·[1–(100m/300m)]0.75 = 0.638 ms–1
Neutral:
σw = 1.25·(0.5m s–1)·[1–0.5·(100m/300m) = 0.521 ms–1
Using a spreadsheet with a range of heights yields:
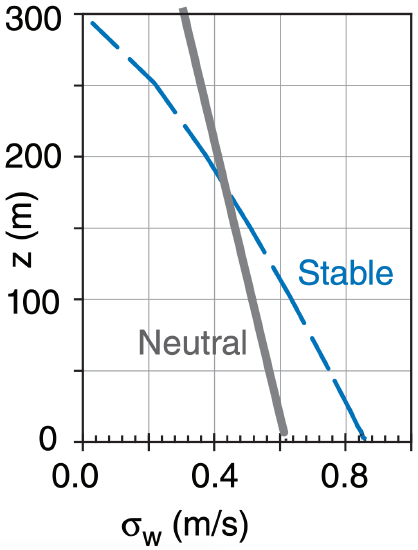
| sigma w (m/s) | ||
|---|---|---|
| z (m) | Stable | Neut. |
| 0.0 | 0.865 | 0.625 |
| 1.0 | 0.863 | 0.624 |
| 10 | 0.843 | 0.615 |
| 100 | 0.638 | 0.521 |
| 150 | 0.514 | 0.469 |
| 200 | 0.379 | 0.417 |
| 250 | 0.266 | 0.365 |
| 300 | 0.0 | 0.313 |
Check: Units OK. Magnitudes OK.
Exposition: Turbulence diminishes rapidly with increasing height for statically stable conditions.
For statically unstable air:
\(\ \begin{align}\sigma_{u}=0.032 \cdot w_{B} \cdot\left(1+\left[1-\left(z / z_{i}\right)\right]^{6}\right)\tag{18.26a}\end{align}\)
\(\ \begin{align}\sigma_{v}=0.032 \cdot w_{B}\tag{18.26b}\end{align}\)
\(\ \begin{align}\sigma_{w}=0.11 \cdot w_{B} \cdot\left(z / z_{i}\right)^{1 / 3} \cdot\left[1-0.8 \cdot\left(z / z_{i}\right)\right]\tag{18.26c}\end{align}\)
where zi is the mixed-layer depth, wB is buoyancy velocity (eq. 3.38 or 18.19b). These relationships are important for air-pollution dispersion, and are used in the Air Pollution chapter. These equations are valid only within the boundary layer (i.e., from z = 0 up to h or zi ).
Sample Application (§)
For a 1 km thick unstable ABL, compare the vertical profiles of σu & σw. Assume wB = 30 m s–1.
Find the Answer
Given: zi = 1000 m , wB = 30 m s–1
Find: σu & σw vs. z .
Use eqs. (18.26a and 18.26c) in a spreadsheet, and plot.
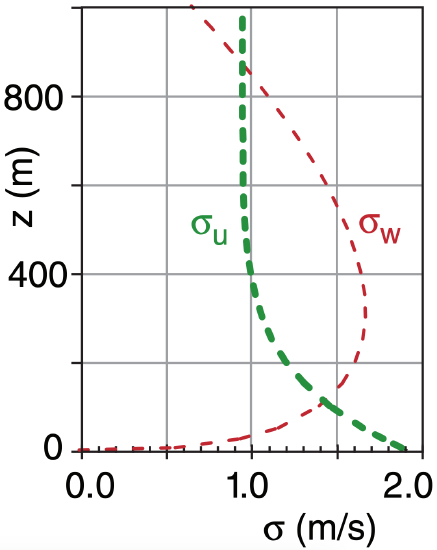
| sigma (m/s) | ||
|---|---|---|
| z (m) | σu | σw. |
| 0 | 1.920 | 0.0 |
| 50 | 1.666 | 1.167 |
| 100 | 1.470 | 1.409 |
| 200 | 1.212 | 1.621 |
| 300 | 0.514 | 1.679 |
| 500 | 0.975 | 1.572 |
| 800 | 0.960 | 1.103 |
| 1000 | 0.960 | 0.660 |
Check: Units OK. Magnitude reasonable.
Exposition: The flow is anisotropic at most heights. Near both the surface and zi , horizontal turbulence is greater than vertical. But in the middle of the mixed layer, vertical turbulence is greater than horizontal.
18.6.3. Isotropy
If turbulence has nearly the same variance in all three directions, then turbulence is said to be isotropic. Namely:
\(\ \begin{align}\sigma_{u}^{2} \approx \sigma_{v}^{2} \approx \sigma_{w}^{2}\tag{18.27}\end{align}\)
[CAUTION: Do not confuse this word with “isentropic”, which means adiabatic or of constant entropy.]
Turbulence is anisotropic (not isotropic) in many situations. During the daytime over bare land, rising thermals create stronger vertical motions than horizontal. Hence, a smoke puff becomes dispersed (i.e., spread out) in the vertical faster than in the horizontal. At night, vertical motions are very weak, while horizontal motions can be larger. This causes smoke puffs to fan out horizontally with only little vertical dispersion in statically stable air.
18.6.4. Turbulence Kinetic Energy
An overall measure of the intensity of turbulence is the turbulence kinetic energy per unit mass (TKE):
\(\ \begin{align}T K E=0.5 \cdot[\overline{\left(u^{\prime}\right)^{2}}+\overline{\left(v^{\prime}\right)^{2}}+\overline{\left(w^{\prime}\right)^{2}}]\tag{18.28a}\end{align}\)
\(\ \begin{align}T K E=0.5 \cdot\left[\sigma_{u}^{2}+\sigma_{v}^{2}+\sigma_{w}^{2}\right]\tag{18.28b}\end{align}\)
TKE is usually produced at eddy sizes that scale to the boundary-layer depth. The production is done mechanically by wind shear and buoyantly by thermals.
Sample Application
Find u* , the velocity standard deviations, and TKE in statically stable air at height 50 m in an ABL that is 200 m thick. Assume CD = 0.002, and the winds at height 10 m are 5 m s–1.
Find the Answer
Given: z = 50 m, h = 200 m, CD = 0.002, M = 5 m s–1. Statically stable.
Find: u* , σu , σv , σw = ? m s–1. TKE = ? m2 s–2.
Use eq. (18.11):
u*2 = 0.002·(5m s–1)2 = 0.05 m2 s–2. u* = 0.22 ms–1
Use eqs. (18.24a-c):
σu = 2·(0.22m s–1)·[1–(50m/200m)]3/4 = 0.35 ms–1
σv = 2.2·(0.22m s–1)·[1–(50m/200m)]3/4 = 0.39 ms–1
σw = 1.73·(0.22m s–1)·[1–(50m/200m)]3/4 = 0.31 ms–1
Use eq. (18.28b):
TKE = 0.5·[0.352 + 0.392 + 0.312] = 0.185 m2 s–2.
Check: Units OK. Physics OK.
Exposition: In statically stable air, vertical turbulence is generally less than horizontal turbulence. Also, turbulence intensity increases with wind speed. If the atmosphere is too stable, then there will be no turbulence (see “dynamic stability” in the Atmospheric Stability chapter).
Turbulent energy cascades through the inertial subrange, where the large-size eddies drive medium ones, which in turn drive smaller eddies. Molecular viscosity continuously damps the tiniest (microscale) eddies, dissipating TKE into heat. TKE is not conserved.
The tendency of TKE to increase or decrease is given by the following TKE budget equation:
\(\ \begin{align}\frac{\Delta T K E}{\Delta t}=A+S+B+T r-\varepsilon\tag{18.29}\end{align}\)
where A is advection of TKE by the mean wind, S is shear generation, B is buoyant production or consumption, Tr is transport by turbulent motions and pressure, and ε is viscous dissipation rate. For stationary (steady-state) turbulence, the tendency term on the left side of eq. (18.29) is zero.
Mean wind blows TKE from one location to another. The advection term is given by:
\(\ \begin{align}A=-U \cdot \frac{\Delta T K E}{\Delta x}-V \cdot \frac{\Delta T K E}{\Delta y}-W \cdot \frac{\Delta T K E}{\Delta z}\tag{18.30}\end{align}\)
Thus, turbulence can increase (or decrease) at any location if the wind is blowing in greater (or lesser) values of TKE from somewhere else.
“Big whirls have little whirls that feed on their velocity, and little whirls have lesser whirls and so on to viscosity – in the molecular sense.”
– L.F. Richardson, 1922: “Weather Prediction by Numerical Process”. Cambridge Univ. Press. p66.
Wind shear generates turbulence near the ground according to:
\(\ \begin{align}S=u_{*}^{2} \cdot \frac{\Delta M}{\Delta z}\tag{18.31a}\end{align}\)
in the surface layer, where u* is the friction velocity, and ∆M/∆z is the wind shear. To good approximation for near-neutral static stability:
\(\ \begin{align}S \approx a \cdot M^{3}\tag{18.31b}\end{align}\)
where a = 2x10–4 m–1 for wind speed M measured at a standard height of z = 10 m. Greater wind speeds near the ground cause greater wind shear, and generate more turbulence.
To get TKE shear-generation eq. (18.31b), start with eq. (18.31a):
\(\ \begin{align}S=u_{*}^{2} \cdot(\partial M / \partial z)\tag{18.31a}\end{align}\)
But
\(\ \begin{align}(\partial M / \partial z)=u_{*} /(k \cdot z)\tag{ from e.q 18.11}\end{align}\)
which gives
\(\ u_{*}^{3}=C_{D}^{3 / 2} \cdot M^{3}\)
Thus:
\(\ S=\left[C_{D}^{3 / 2} /(k \cdot z)\right] \cdot M^{3}\)
or
\(\ \begin{align}S=a \cdot M^{3}\tag{18.31}\end{align}\)
where
\(\ a=\left[C_{D}^{3 / 2} /(k \cdot z)\right]\)
For CD ≈ 0.01, k = 0.4 (von Kármáns constant), and z = 10 m, the result is a = 2.5x10–4 m–1. For any wind speed, shear generation can vary by an order of magnitude depending on the drag coefficient and height.
Buoyancy can either increase or decrease turbulence. When thermals are rising from a warm surface, they generate TKE. Conversely, when the ground is cold and the ABL is statically stable, buoyancy opposes vertical motion and consumes TKE.
The rate of buoyant production or consumption of TKE is:
\(\ \begin{align}B=\frac{|g|}{T_{v}} \cdot F_{H s f c}\tag{18.32}\end{align}\)
where |g|= 9.8 m·s–2 is gravitational acceleration magnitude, Tv is the absolute virtual air temperature near the ground, and FH sfc is the kinematic effective surface heat flux (positive when the ground is warmer than the air). Over land, FH sfc and B are usually positive during the daytime, and negative at night.
Turbulence can advect or transport itself. For example, if turbulence is produced by shear near the ground (in the surface layer), then turbulence motions will tend to move the excess TKE from the surface layer to locations higher in the ABL. Pressure fluctuations can have a similar effect, because turbulent pressure forces can generate turbulence motions. This pressure term is difficult to simplify, and will be grouped with the turbulent transport term, Tr, here.
\(\ \begin{align}\varepsilon \approx \frac{(T K E)^{3 / 2}}{L_{\varepsilon}}\tag{18.33}\end{align}\)
where Lε ≈ 50 m is a dissipation length scale.
The ratio of buoyancy to shear terms of the TKE equation is called the flux Richardson number, Rf :
\(\ \begin{align}R_{f}=\frac{-B}{S} \approx \frac{-\left(|g| / T_{v}\right) \cdot F_{H\ s f c}}{u_{*}^{2} \cdot \frac{\Delta M}{\Delta z}} \tag{18.34a}\end{align}\)
\(\ \begin{align}R_{f} \approx \frac{-\left(|g| / T_{v}\right) \cdot F_{H\ s f c}}{a \cdot M^{3}}\tag{18.34b}\end{align}\)
with a ≈ 2x10–4 m–1. Rf is approximately equal to the gradient or bulk Richardson number, discussed in the Stability chapter. Generally, turbulence dies if Rf > 1.
Sample Application
Assume steady state, and neglect advection and transport. What equilibrium TKE is expected in the surface layer with a mean wind of 5 m s–1 and surface heat flux of –0.02 K·m s–1? The ambient temperature is 25°C, and the air is dry.
Find the Answer
Given: M = 5 m s–1, FH sfc = –0.02 K·m s–1, A = 0, Tr = 0, ∆TKE/∆t = 0 for steady state, Tv = 298 K.
Find: TKE = ? m2 s–2 .
Rearrange eq. (18.29).
ε = S + B
But ε depends on TKE, thus, we can rearrange eq. (18.33) to solve for TKE = ( Lε · [ε] )2/3 and then plug in the eq. above:
TKE = { Lε · [S + B] }2/3
Use eqs. (18.31b and 18.32) to find S and B, and plug into the equation above:
\(\ T K E=\left\{L_{\varepsilon} \cdot\left[a \cdot M^{3}+\left(|g| / T_{v}\right) \cdot F_{H s f c}\right]\right\}^{2 / 3}=\{(50 \mathrm{m})\)
\(\left.\left[\left(2 \times 10^{-4} \mathrm{m}^{-1}\right)\left(5 \frac{\mathrm{m}}{\mathrm{s}}\right)^{3}+\frac{9.8 \mathrm{ms}^{-2}}{298 \mathrm{K}}(-0.02 \mathrm{Km} / \mathrm{s})\right]\right\}^{2 / 3}\)
= {1.25 – 0.033 m3 s–3 } 2/3 = 1.14 m2 s–2
Check: Units OK. Physics OK.
Exposition: This turbulence intensity is weak, as is typical at night when heat fluxes are negative. Also, eq. (18.31b) for S is not accurate for statically stable conditions.
18.6.5. Free and Forced Convection
The nature of turbulence, and therefore the nature of pollutant dispersion, changes with the relative magnitudes of terms in the TKE budget. Two terms of interest are the shear (S) and buoyancy (B) terms.

When |B| < |S/3|, the atmosphere is said to be in a state of forced convection (Fig. 18.24). These conditions are typical of windy overcast days, and are associated with near neutral static stability. Turbulence is nearly isotropic. Smoke plumes disperse at nearly equal rates in the vertical and lateral, which is called coning. The sign of B is not important here — only the magnitude.
When B is positive and |B| > |3·S|, the atmosphere is said to be in a state of free convection. Thermals of warm rising air are typical in this situation, and the ABL is statically unstable (in the nonlocal sense; see the Stability chapter). These conditions often happen in the daytime over land, and during periods of cold-air advection over warmer surfaces. Turbulence is anisotropic, with more energy in the vertical, and smoke plumes loop up and down in a pattern called looping.
When B is negative and |B| > |S|, static stability is so strong that turbulence cannot exist. During these conditions, there is virtually no dispersion while the smoke blows downwind. Buoyancy waves (gravity waves) are possible, and appear as waves in the smoke plumes. For values of |B| ≈ |S|, breaking Kelvin-Helmholtz waves can occur (see the Stability chapter), which cause some dispersion.
When B is negative but |B| < |S|, weak turbulence is possible. These conditions can occur at night. This is sometimes called stably-stratified turbulence (SST). Vertical dispersion is much weaker than lateral, causing an anisotropic condition where smoke spreads horizontally more than vertically, in a process called fanning.
Fig. 18.24 shows the relationship between different types of convection and the terms of the TKE equation. While the ratio of B/S determines the nature of convection, the sum S + B determines the intensity of turbulence. A Pasquill-Gifford turbulence type (Fig. 18.24) can also be defined from the relative magnitudes of S and B, and is used in the Air Pollution chapter to help estimate pollution dispersion rates.
Sample Application
For the previous Sample Application, determine the nature of convection (free, forced, etc.), the Pasquill-Gifford (PG) turbulence type, and the flux Richardson number. Assume no clouds.
Find the Answer
Given: (see previous Sample Application)
Find: S = ? m2 s–3 , B = ? m2 s–3 , Rf = ? , PG = ?
Use eq. (18.31b):
\(\ S \approx\left(2 \times 10^{-4} \mathrm{m}^{-1}\right)\left(5 \frac{\mathrm{m}}{\mathrm{s}}\right)^{3}=0.025 \mathrm{m}^{2} \mathrm{s}^{-3}\)
Use eq. (18.32):
\( B=\frac{9.8 \mathrm{ms}^{-2}}{298 \mathrm{K}}(-0.02 \mathrm{Km} / \mathrm{s})=-0.00066 \mathrm{m}^{2} \mathrm{s}^{-3}\)
Because the magnitude of B is less than a third of that of S, we conclude convection is forced.
Use eq. (18.34): Rf = –(–0.00066) / 0.025 = 0.0264 and is dimensionless.
Use Fig. 18.24. Pasquill-Gifford Type = D (but on the borderline near E).
Check: Units OK. Physics OK.
Exposition: The type of turbulence is independent of the intensity. Intensity is proportional to S+B.
18.6.6. Turbulent Fluxes and Covariances
Seen on a bumper sticker:
“Lottery: A tax on people who are bad at math.”
Rewrite eq. (18.22) for variance of w as
\(\ \operatorname{var}(w)=\frac{1}{N} \sum_{k=1}^{N}\left(W_{k}-\bar{W}\right) \cdot\left(W_{k}-\bar{W}\right)\)
By analogy, a covariance between vertical velocity w and potential temperature θ can be defined as:
\(\ \begin{align}\begin{array}{l}
\operatorname{covar}(w, \theta)=\frac{1}{N} \sum_{k=1}^{N}\left(W_{k}-\bar{W}\right) \cdot\left(\theta_{k}-\bar{\theta}\right) \\
\quad=\frac{1}{N} \sum_{k=1}^{N}\left(w_{k}^{\prime}\right) \cdot\left(\theta_{k}^{\prime}\right) \\
\quad=\overline{w^{\prime} \theta^{\prime}}
\end{array}\tag{18.36}\end{align}\)
where the overbar still denotes an average. Namely, one over N times the sum of N terms (see middle line of eq. 18.36) is the average of those items. Comparing eqs. (18.35) with (18.36), we see that variance is just the covariance between a variable and itself.
Covariance indicates the amount of common variation between two variables. It is positive where both variables increase and/or decrease together. Covariance is negative for opposite variation, such as when one variable increases while the other decreases. Covariance is zero if one variable is unrelated to the variation of the other.
The correlation coefficient ra,b is defined as the covariance between a and b, normalized by the standard deviations of those two variables. By normalized, we mean that –1 ≤ ra,b ≤ 1. Using vertical velocity and potential temperature for illustration:
\(\ \begin{align} r_{w, \theta}=\frac{\overline{w^{\prime} \theta^{\prime}}}{\sigma_{w} \cdot \sigma_{\theta}}\tag{18.37}\end{align}\)
A correlation coefficient of +1 indicates a perfect correlation (both variables increase or decrease together proportionally), –1 indicates perfect opposite correlation, and zero indicates no correlation. Because it is normalized, ra,b gives no information on the absolute magnitudes of the variations.
In the ABL, many turbulent variables are correlated. For example, in the statically unstable ABL (Fig. 18.25a), parcels of warm air rise and while other cool parcels sink in convective circulations. Warm air (θ’ = +) going up (w’ = +) gives a positive product [ (w’θ’)up = + ]. Cool air (θ’ = –) going down (w’ = –) also gives a positive product [ (w’θ’)down = + ].
The average of those two products is also positive \left[\overline{w^{\prime} \theta^{\prime}}=0.5 \cdot\left(\left(w^{\prime} \theta^{\prime}\right)_{u p}+\left(w^{\prime} \theta^{\prime}\right)_{d o w n}\right)=+\right]. The result gives positive correlation coefficients rw,θ during free convection, which is typical during daytime.

Sample Application (§ )
Fast-response measurements of potential temperature θ, water-vapor mixing ratio r, and u and w components of wind are given below as a function of time t. For θ and w, find their means, variances, and standard deviations. Also find the covariance, correlation coefficient, kinematic heat flux, and the heat flux (W m–2).
Columns C and D are not used in this example, but will be used in some of the homeworks.
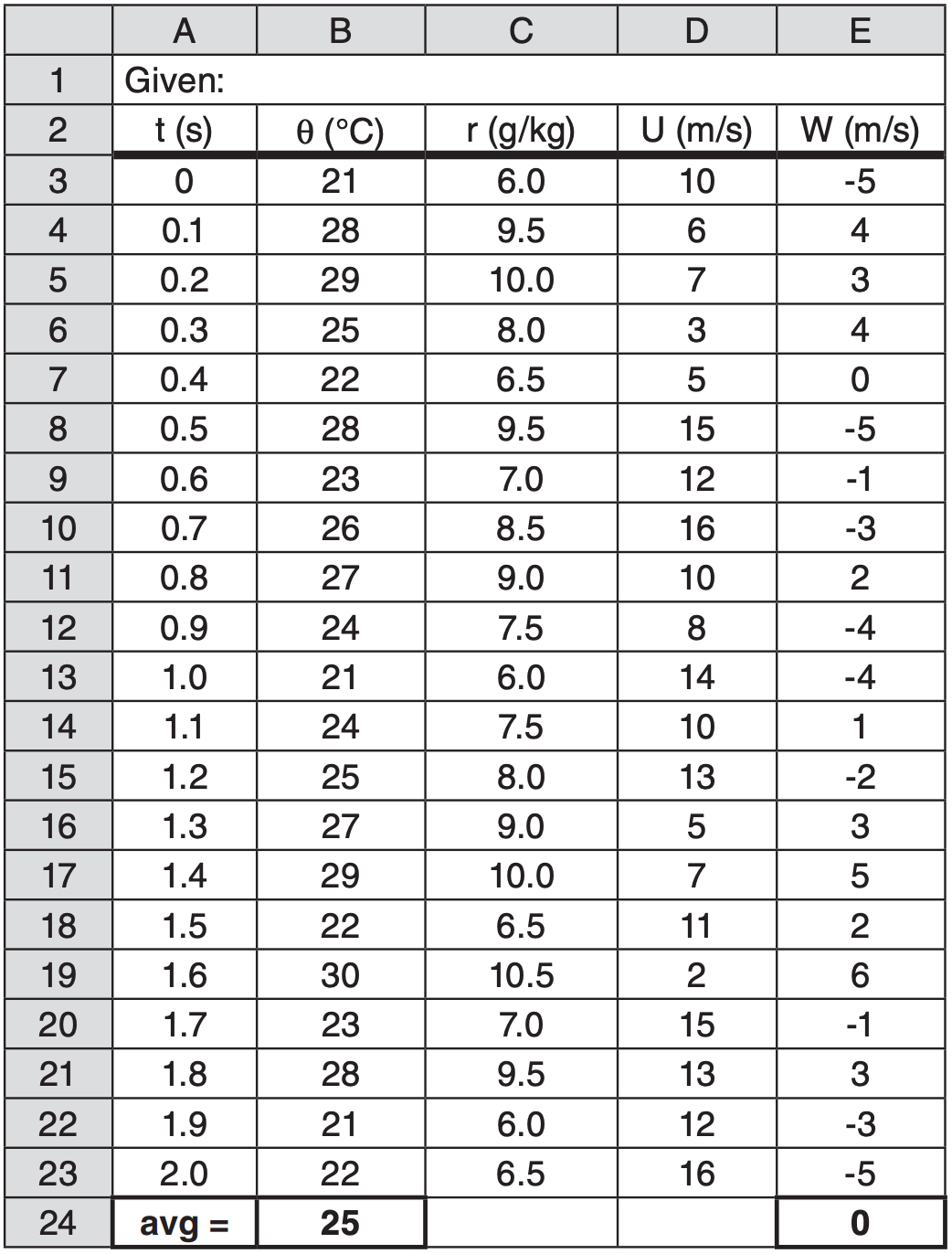
Find the Answer:
Given: Data above in rows 2 through 23.
\(\ \begin{aligned}
&\text { Find: } \bar{W}=? \mathrm{m} \mathrm{s}^{-1}, \quad \bar{\theta}=?^{\circ} \mathrm{C}, \quad \sigma_{w}^{2}=? \mathrm{m}^{2} \mathrm{s}^{-2}\\
&\sigma_{\theta}^{2}=?^{\circ} \mathrm{C}^{2}, \quad \sigma_{w}=? \mathrm{m} \mathrm{s}^{-1}, \quad \sigma_{\theta}=?^{\circ} \mathrm{C}\\
&\overline{w^{\prime} \theta^{\prime}}=? \mathrm{K} \cdot \mathrm{m} \mathrm{s}^{-1}, \quad r_{w, \theta}=? \text { (dimensionless) }\\
&F_{H}=? \mathrm{K} \cdot \mathrm{m} \mathrm{s}^{-1}, \quad \mathbb{F}_{H}=? \mathrm{W} \mathrm{m}^{-2}
\end{aligned}\)
First, use eq. (18.21) to find the mean values. These answers are already shown in row 24 above.
\(\ \bar{\theta}=\underline{\bf{25^{\circ} \mathrm{C}}}, \quad \bar{W}=\underline{\bf{0 \mathrm{m} \mathrm{s}^{-1}}}\)
Next, use eqs. (18.20) to find the deviation from the mean, for each of the observations. The results are tabulated in columns G and H on the next page. Then square each of those perturbation (primed) values, as tabulated in columns I and J on the next page.
Use eq. (18.22), averaging the squared perturbations to give the variances (row 24, columns I and J):
\( \sigma_{\theta}^{2}=\underline{\mathbf{8.48}^{\circ} \mathbf{C}^{2}}, \quad \sigma_{w}^{2}=\underline{\mathbf{12.38} \mathrm{m}^{2} \mathrm{s}^{-2}}\)
The square root of those answers (eq. 18.23) gives the standard deviations in row 25, columns I and J:
\( \sigma_{\theta}=\underline{\mathbf{2.91}^{\circ} \mathbf{C}}, \quad \sigma_{w}=\underline{\mathbf{3 . 5 2} \mathbf{m} \mathrm{s}^{-1}}\)
Use eq. (18.36) and multiply each \(\ w^{\prime}\) with \(\ \theta^{\prime}\) to give in column K the values of \(\ w^{\prime} \theta^{\prime}\). Average those to get the covariance: \(\ \overline{w^{\prime} \theta^{\prime}}=F_{H}=\underline{\bf{6.62 \mathrm{K} \cdot \mathrm{m} \mathrm{s}^{-1}}}\), which is the kinematic heat flux by definition.
Use eq. (18.37) and divide the covariance by the standard deviations to give the correlation coef: \(\ r_{w, \theta}=\underline{\mathbf{0 .65}}\) (dimensionless).
Use eq. (2.11) to give heat flux, with ρ·Cp =1231 (W m–2)/(°C·m s–1) from Appendix B, yielding FH = ρ·Cp·FH = 8150 W m–2.
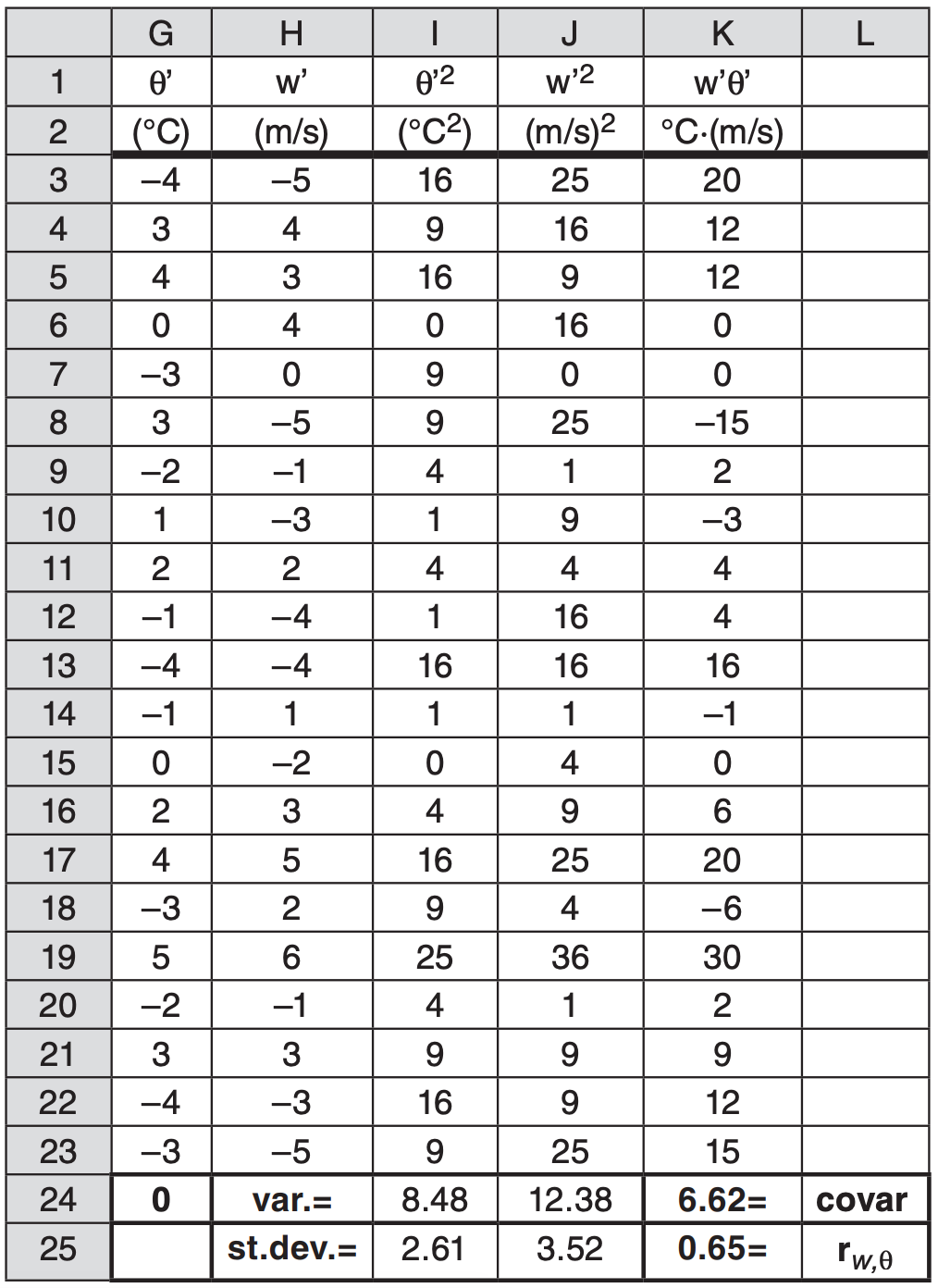
Check: The average is zero of the singled primed values, as they always should be. Units OK.
Exposition: The magnitude of FH is unrealistically big for this contrived data set.
Conversely, for statically stable conditions (Fig. 18.25b) where wind-shear-induced turbulence drives vertical motions against the restoring buoyant forces (see the Stability chapter), one finds cold air moving up, and warm air moving down. (Parcel warmth or coldness is measured relative to the ambient mean potential temperature \(\ \bar{θ}\) at the same ending height as the parcel.) This gives \(\ \overline{ w' θ'}\) < 0 (i.e., \(\ \overline{ w' θ'}\) = – ), which is often the case during night.
More important than the statistics are the physical processes they represent. Covariances represent fluxes. Look at the air parcels crossing the horizontal dashed line in Fig. 18.25a. Pretend that the dashed line is an edge view of a horizontal area of 1 m2.
During time interval ∆t, the warm (light-grey shaded) air parcel moves warm air upward through that area in Fig. 18.25a. Heat flux is defined as heat moved per area per time. Thus this rising warm air parcel contributes to a positive heat flux. Similarly, the cold sinking air parcel (shaded dark grey) contributes to a positive heat flux through that area (because negative w’ times negative θ’ is positive). Both parcels contribute to a positive heat flux.
This implies that covariance between vertical velocity and potential temperature is a turbulent kinematic heat flux, FH [ = Fz turb(θ) in the notation of the Heat chapter]:
\(\ \begin{align}\overline{w^{\prime} \theta^{\prime}}=F_{H}\tag{18.38a}\end{align}\)
Similarly, the covariance between vertical velocity w and water vapor mixing ratio, r (see the Water Vapor chapter), is a kinematic moisture flux, Fz turb(r) :
\(\ \begin{align}\overline{w^{\prime} r^{\prime}}=F_{z\ turb}(r)\tag{ 18.38b}\end{align}\)
Momentum flux is even more interesting. Recall from physics that momentum is mass times velocity. Units would be kg·m·s–1. Therefore, momentum flux (momentum per area per time) would have units of (kg·m·s–1)·m–2·s–1 = (kg·m·s–2)·m–2 = N·m–2. [see Appendix A to relate a force of 1 Newton (N) to other units]. But N·m–2 is a force per unit area, which is the definition of stress, \(\ \tau\). Thus, stress and momentum flux are physically the same in a fluid such as air.
A kinematic momentum flux is the momentum flux divided by air density ρ, which from the paragraph above is equal to \(\ \tau\)/ρ. But this is just the definition of friction velocity squared u*2 (eq. 18.10).
As in Fig. 18.25, if vertically moving air parcels (w’) transport air with different horizontal velocities (u’) across a horizontal area per unit time, then the covariance between vertical velocity and horizontal velocity is a kinematic momentum flux. From the paragraph above, the magnitude is also equal to the friction velocity squared. Thus:
\(\ \begin{align}|\overline{w^{\prime} u^{\prime}}|=| F_{z\ turb }(\text { momentum })|=| \tau / \rho |=u_{*}^{2}\tag{18.38c}\end{align}\)
where \(\overline{w^{\prime} u^{\prime}}\) is called a Reynolds stress.
In Fig. 18.25, air mass is conserved. Namely, each rising air parcel is compensated by a descending air parcel with the same air mass. Thus, as seen from the discussion above, turbulence can cause a net vertical transport of heat, moisture, and momentum, even though there is no net transport of air mass.
Turbulent fluxes given by eqs. (18.38) are called eddy-correlation fluxes. They can be measured with fast response velocity, humidity, and temperature sensors, sampling at about 10 Hz for 30 minutes. Turbulent fluxes can also be parameterized, as discussed next.
18.6.7. Turbulence Closure
To forecast the weather (see the NWP chapter), we need to solve the Eulerian conservation equations for temperature, humidity, and wind:
- temperature forecasts ← heat conservation eq. ← First Law of Thermodynamics (see the Thermodynamics chapter)
- humidity forecasts ← water conservation eq. ← Eulerian water-budget equation (see the Water Vapor chapter)
- wind forecasts ← momentum conservation eq. ← Newton’s Second Law (see the Atmos. Forces & Winds chapter)
For example, the Eulerian net heat-budget equation from the Thermodynamics chapter (eq. 3.51) is:
\(\ \begin{align}\frac{\Delta T}{\Delta t}=\text { Advection + Radiation + LatentHeat - } \frac{\Delta F_{z\ turb }(\theta)}{\Delta z} \tag{18.39a}\end{align}\)
where the last term is the turbulence term. But from eq. (18.38a), we recognize the turbulent heat flux as a covariance. Thus, eq. (18.39a) can be rewritten as:
\(\ \begin{align}\frac{\Delta \bar{T}}{\Delta t}=(\text {otherPhysics})-\frac{\Delta \overline{w^{\prime} \theta^{\prime}}}{\Delta z}\tag{18.39b}\end{align}\)
Sample Application
If \(\ \overline{w^{\prime} \theta^{\prime}}\) = 0.2 K·m s–1 at the surface, and is 0 at the top of a 1 km thick layer, find the warming rate.
Find the Answer
Given: \(\ \overline{w^{\prime} \theta^{\prime}}\) = 0.2 K·m s–1 at z = 0, \(\ \overline{w^{\prime} \theta^{\prime}}\) =0 at z = 1km
Find: \(\ \Delta \bar{T} / \Delta t=? \mathrm{K} \mathrm{h}^{-1}\)
Use eq. (18.39b):
\(\ \Delta \bar{T} / \Delta t=-\left(0-0.2 \mathrm{Km} \mathrm{s}^{-1}\right) /(1000 \mathrm{m}-0)\)
= 2x10–4 K s–1 = 0.72 K h–1.
Check: Units OK. Magnitude small.
Exposition: Over 12 hours of daylight, this surface flux would warm the thick layer of air by 8.6°C.
The derivation of this equation is shown in the HIGHER MATH box on the next page.
Because the heat flux \(\ \overline{w^{\prime} \theta^{\prime}}\) is needed in eq. (18.39b), we need to get a forecast equation for it:
\(\ \begin{align}\frac{\Delta \overline{w^{\prime} \theta^{\prime}}}{\Delta t}=(\text {otherPhysics})-\frac{\Delta \overline{w^{\prime} w^{\prime} \theta^{\prime}}}{\Delta z}\tag{18.40}\end{align}\)
But this contains yet another unknown \(\ \overline{w^{\prime} w^{\prime} \theta^{\prime}}\). A forecast equation for \(\ \overline{w^{\prime} w^{\prime} \theta^{\prime}}\) would yield yet another unknown. Hence, we need an infinite number of equations just to forecast air temperature. Or, if we use only a finite number of equations, then we have more unknowns than equations.
Hence, this set of equations is mathematically not closed, which means they cannot be solved. To be a closed system of equations, the number of unknowns must equal the number of equations.
One reason for this closure problem is that it is impossible to accurately forecast each swirl and eddy in the wind. To work around this problem, meteorologists parameterize the net effect of all the eddies; namely, they use a finite number of equations, and approximate the unknowns as a function of known variables. Such an approximation is called turbulence closure, because it mathematically closes the governing equations, allowing useful weather forecasts and engineering designs.
Why does a turbulence covariance term appear in the forecast equation for average temperature, \(\ \bar{T}\)? To answer, consider the vertical advection term (3.31) in the heat-budget equation (3.17) as an example:
\(\ \frac{\partial T}{\partial t}=\cdots-W \frac{\partial \theta}{\partial z}\)
For each dependent variable (T, W, θ), describe them by their mean plus turbulent parts:
\(\ \frac{\partial\left(\bar{T}+T^{\prime}\right)}{\partial t}=\cdots-\left(\overline{W}+w^{\prime}\right) \frac{\partial\left(\bar{\theta}+\theta^{\prime}\right)}{\partial z}\)
or
\(\ \frac{\partial \bar{T}}{\partial t}+\frac{\partial T^{\prime}}{\partial t}=\cdots-\overline{W} \frac{\partial \bar{\theta}}{\partial z}-\overline{W} \frac{\partial \theta^{\prime}}{\partial z}-w^{\prime} \frac{\partial \bar{\theta}}{\partial z}-w^{\prime} \frac{\partial \theta^{\prime}}{\partial z}\)
Next, average the whole equation. But the average of a sum is the same as the sum of the averages:
\(\ \frac{\overline{\partial \bar{T}}}{\partial t}+\frac{\overline{\partial T^{\prime}}}{\partial t}=\cdots-\overline{\overline{W} \frac{\partial \bar{\theta}}{\partial z}}-\overline{\overline{W} \frac{\partial \theta^{\prime}}{\partial z}}-w^{\prime} \frac{\partial \bar{\theta}}{\partial z}-w^{\prime} \frac{\partial \theta^{\prime}}{\partial z}\)
[Aside: Let A be any variable. Expand into mean and turbulent parts: \(\ A=\bar{A}+a^{\prime}\), then average the whole eq: \(\ \bar{A}=\overline{\bar{A}}+\bar{a}^{\prime}\). But the average of an average is just the original average: \(\ \bar{A}=\bar{A}+\bar{a}\). This equation can be valid only if \(\ \overline{a^{\prime}}=0\). Thus, the average of any term containing a single primed variable (along with any number of unprimed variables) is zero. ]
Thus the heat budget becomes:
\(\ \frac{\overline{\partial \bar{T}}}{\partial t}=\dots-\overline{\overline{W} \frac{\partial \bar{\theta}}{\partial z}}-w^{\prime} \frac{\partial \theta^{\prime}}{\partial z}\)
The term on the left and the first term on the right are averages of averages, and can be rewritten as just the original averages. The last term can be transformed into flux form using the turbulent continuity equation (which works if you apply it to the turbulent advection in all 3 directions, but which is not shown here). The end result is:
\(\ \frac{\partial \bar{T}}{\partial t}=\dots-\overline{W} \frac{\partial \bar{\theta}}{\partial z}-\frac{\partial \overline{w^{\prime} \theta^{\prime}}}{\partial z}\)
This says that to forecast the average temperature, you need to consider not only the average advection by the mean wind (first term on the right), but you also need to consider the turbulence flux divergence (last term on the right).
Similar terms appear for advection in the x and y directions. Also, similar terms appear in the forecast equations for moisture and wind. Thus, the effects of turbulence cannot be neglected.
To simplify the notation in almost all of this book, the overbar is left off of the terms for mean temperature, mean wind, etc. Also, earlier in this chapter, and in other chapters, the turbulence flux divergence term was parameterized directly as a function of non-turbulent (average) wind, temperature, humidity, etc. Such parameterizations are turbulence closure approximations.
18.6.7.1. Turbulence Closure Types
For common weather situations with mean temperature, wind and humidity that are nearly horizontally uniform, turbulent transport in any horizontal direction nearly cancels transport in the opposite direction, and thus can be neglected. But vertical transport is significant. Medium- and largesized turbulent eddies can transport air parcels from many different source heights to any destination height within the turbulent domain, where the smaller eddies mix the parcels together.
Different approximations of turbulent transport consider the role of small and large eddies differently. Local closures, which neglect the large eddies, are most common. This gives turbulent heat fluxes that flow down the local gradient of potential temperature, analogous to molecular diffusion or conduction (see the Heat and Air Pollution chapters). One such turbulence closure is called K-theory.
A nonlocal closure alternative that accounts for the superposition of both large and small eddies is called transilient turbulence theory (T3). While this is more accurate, it is also more complicated. There are many other closures that have been proposed. K-theory is reviewed here.
18.6.7.2. K-Theory
One approximation to turbulent transport considers only small eddies. This approach, called K-theory, gradient transport theory, or eddy-diffusion theory, models turbulent mixing analogously to molecular diffusion For example, heat flux FH can be modeled as:
\(\ \begin{align} F_{H}=\overline{w^{\prime} \theta^{\prime}}=-K \cdot \frac{\Delta \bar{\theta}}{\Delta z}\tag{18.41a}\end{align}\)
This parameterization says that heat flows down the gradient of potential temperature, from warm to cold. The rate of this turbulent transfer is proportional to the parameter K, called the eddy viscosity or eddy diffusivity, with units m2·s–1.
Similar expressions can be made for moisture flux as a function of the mean mixing-ratio (r) gradient, or momentum flux as a function of the shear in horizontal wind components (U, V):
\(\ \begin{align}\overline{w^{\prime} r^{\prime}}=-K \frac{\Delta \bar{r}}{\Delta z} \tag{18.41b}\end{align}\)
\(\ \begin{align}\overline{w^{\prime} u^{\prime}}=-K \frac{\Delta \bar{U}}{\Delta z}\tag{18.41c}\end{align}\)
\(\ \begin{align}\overline{w^{\prime} v^{\prime}}=-K \frac{\Delta \bar{V}}{\Delta z}\tag{18.41d}\end{align}\)
K is expected to be larger for more intense turbulence. In the surface layer, turbulence is generated by wind shear. Prandtl made a mixing-length suggestion that:
\(\ \begin{align}K=k^{2} \cdot z^{2} \cdot\left|\frac{\Delta \bar{M}}{\Delta z}\right|\tag{18.42}\end{align}\)
where k = 0.4 is von Kármán’s constant (dimensionless), z is height above ground, and ∆M/∆z is mean shear of the horizontal wind M.
When K-theory is used in the Eulerian heat budget equation, neglecting all other terms except turbulence, the result gives the heating rate of air at height z due to turbulent flux divergence (i.e., change of flux with height):
\(\ \begin{align}\frac{\Delta \bar{\theta}(z)}{\Delta t}=K \cdot\left[\frac{\bar{\theta}(z+\Delta z)-2 \bar{\theta}(z)+\bar{\theta}(z-\Delta z)}{(\Delta z)^{2}}\right]\tag{18.43}\end{align}\)
{For those of you who like calculus, the ratio in square brackets is an approximation to the second derivative \(\ \left[\partial^{2} \bar{\theta} / \partial z^{2}\right]\). Namely, it is equal to the curvature of the potential temperature vertical profile.} Although the example above was for heat flux, you can also use it for moisture or momentum flux by substituting \(\ \bar{r}, \bar{U}, \text { or } \bar{V}\) in place of \(\ \bar{\theta}\).
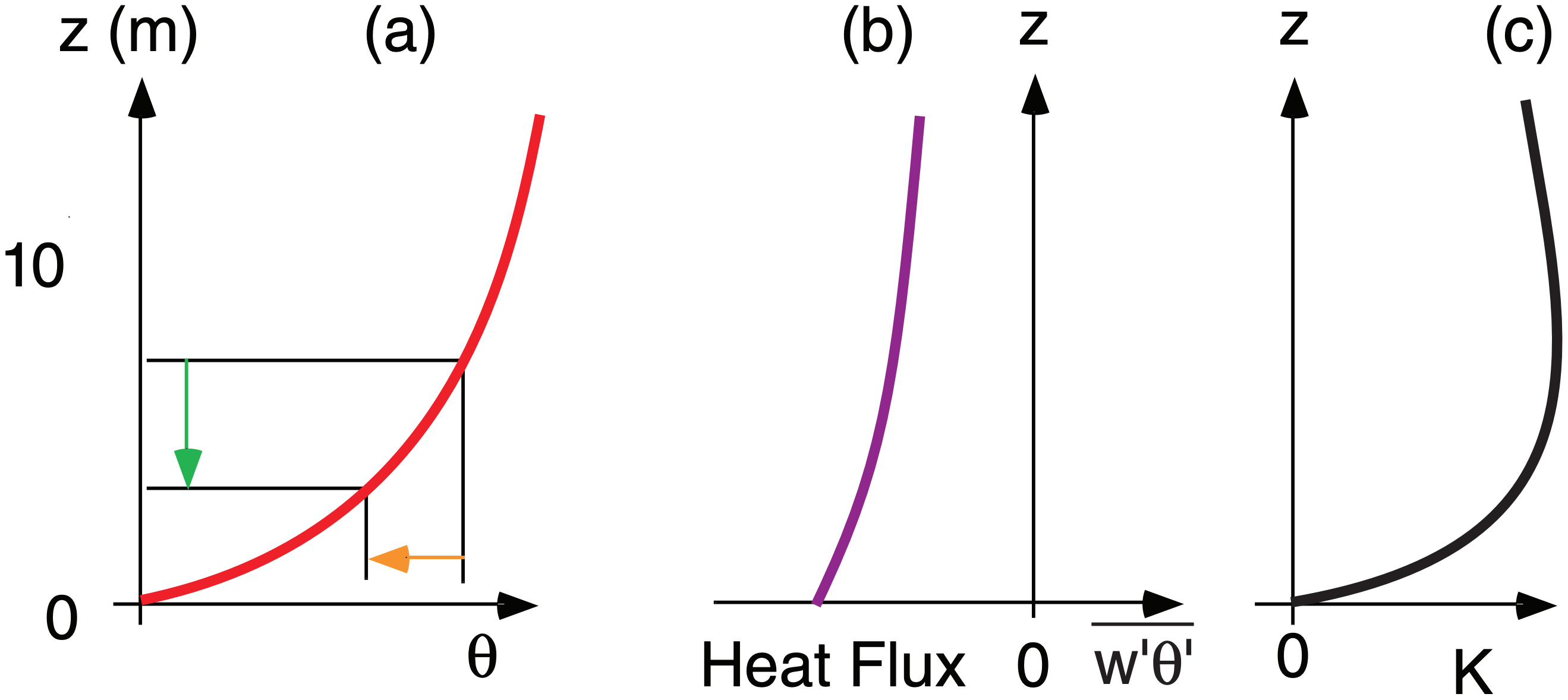
K-theory works best for windy surface layers, where turbulent eddy sizes are relatively small. The green arrow in Fig. 18.26a shows that heat flux flows “down” the temperature gradient from warmer to colder potential temperature (orange arrow), which gives a negative (downward) heat flux (Fig 18.26b) in the statically stable surface layer. Fig. 18.25 is also a small-eddy (K-theory-like) illustration.
K-theory does not apply at the solid ground, but only within the air where turbulence exists. For heat fluxes at the surface, use approximations given in earlier in this chapter, and in the Heat chapter.
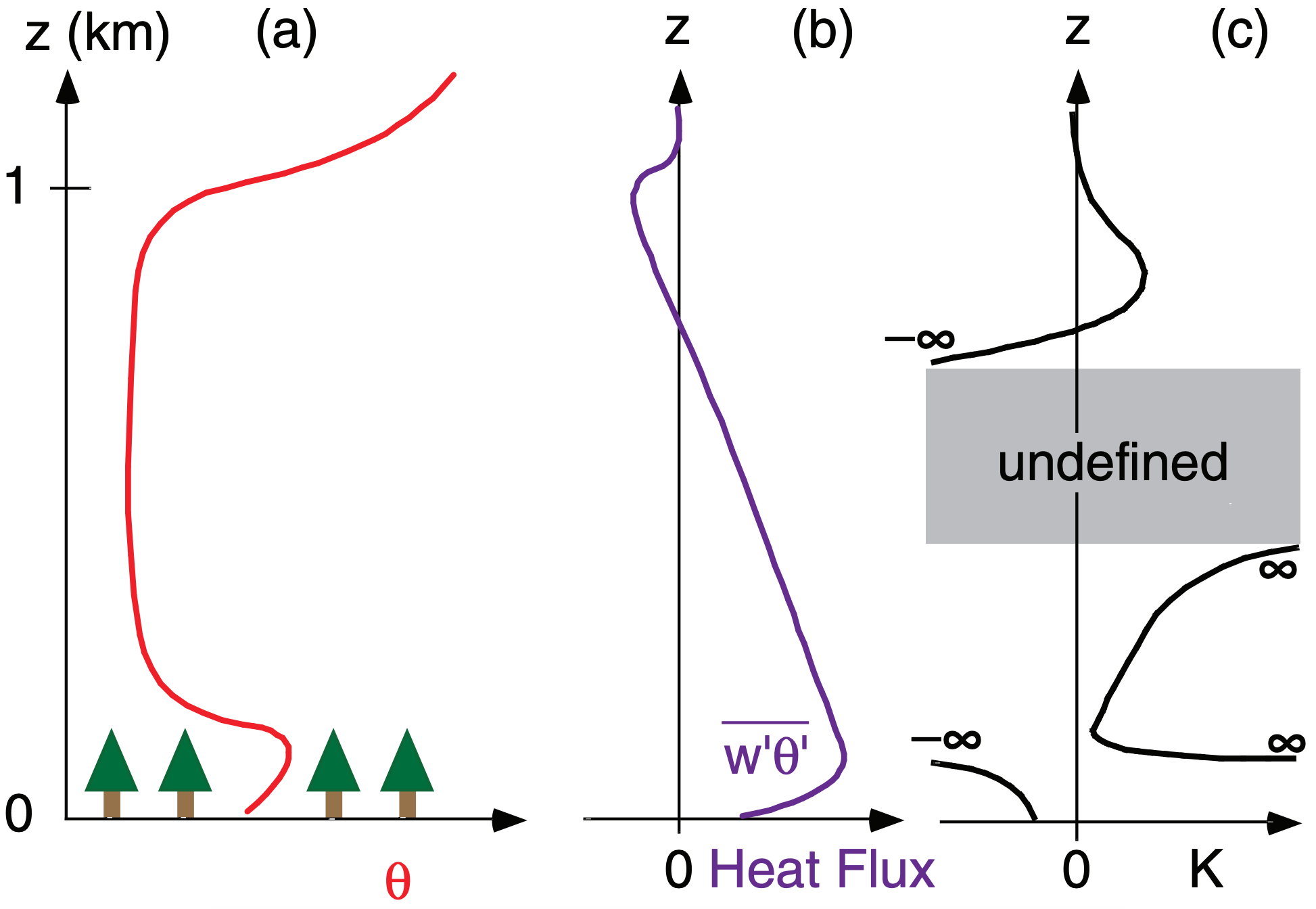
K-theory has difficulty with convective ABLs and should not be used there. Figs. 18.27a & b illustrate these difficulties, giving typical values in the atmosphere, and the resulting K values computed from eq. (18.42). Negative and infinite K values are unphysical.
18.6.7.3. Nonlocal Closure
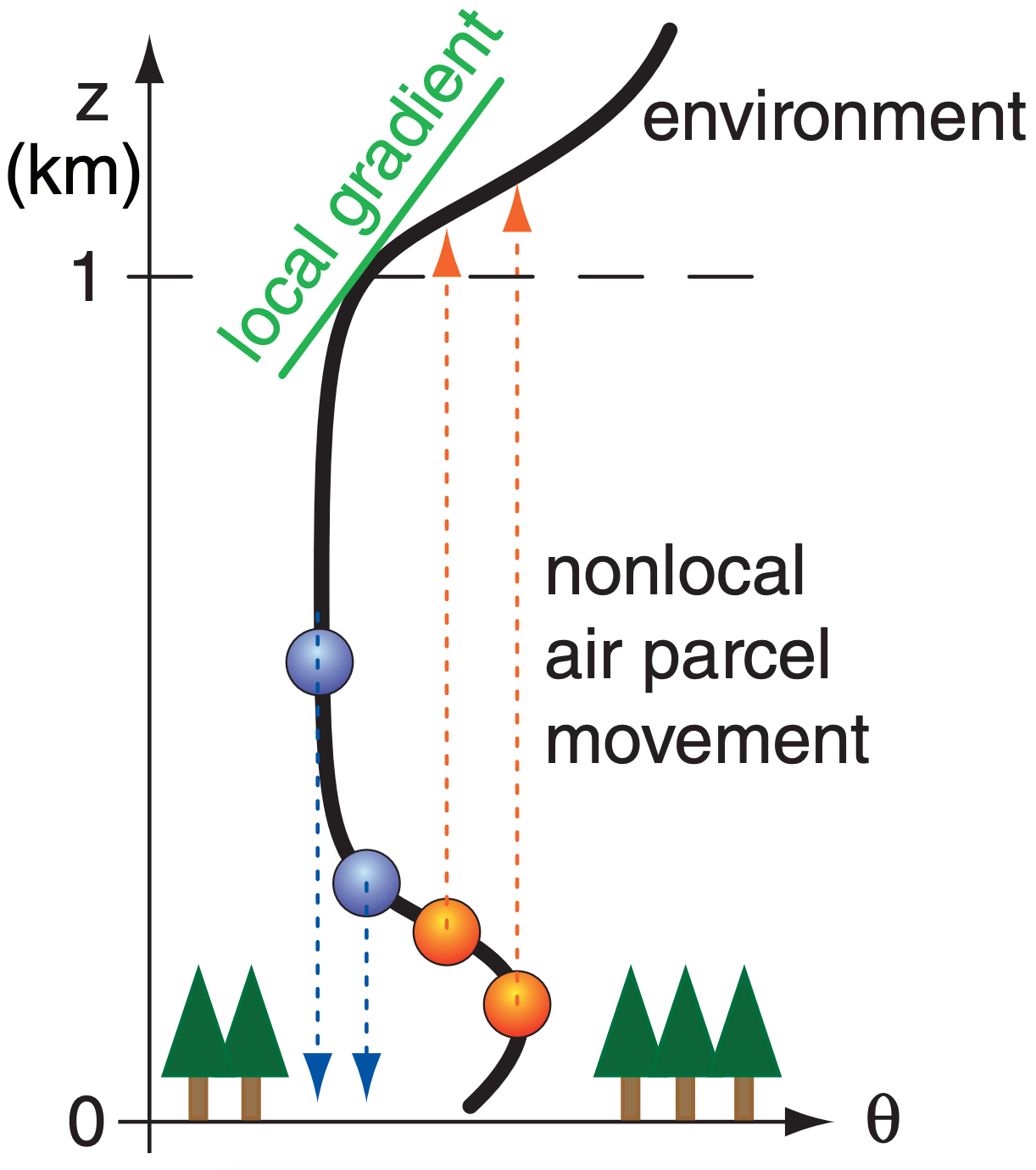
Instead of looking at local down-gradient transport as was done in K-theory, you can look at the full range of distances across that air parcels move in turbulent conditions (Fig. 18.28). This is an approach called nonlocal closure, and is useful for a statically unstable ABL having free convection. [You might want to review the “parcel (apex) method” in Chapter 5 for determining nonlocal static stability.]
For heat flux at the altitude of the dashed line in Fig. 18.28, K-theory (small-eddy theory) would utilize the local gradient of θ at that altitude, and conclude that the heat flux should be downward and of a certain magnitude. However, if the larger-size eddies are also included (as in nonlocal closure), such as the parcel rising from tree-top level, we see that it is bringing warm air upward (a positive contribution to heat flux). This could partially or completely counteract the negative contribution to flux caused by the local small eddies.
As you can probably anticipate, a better approach would be to consider eddies of all sizes and the associated nonlocal air-parcel movements. One such approach is called transilient turbulence theory (T3). This approach uses arrays to account for eddies of each different size, and combines them to find the average effect of all eddy sizes. It is more complex, and will not be described here.
Sample Application
Instruments on a tower measure θ = 15°C and M = 5 m s–1 at z = 4 m, and θ = 16°C and M = 8 m s–1 at z = 10 m. What is the vertical heat flux?
Find the Answer
Given:
| z (m) | θ (°C) | M (m s–1) |
| 10 | 16 | 8 |
| 4 | 15 | 5 |
Find: FH = ? K·m s–1
First, use eq. (18.42), at average z = (10+4)/2 = 7 m
\(\ K=k^{2} \cdot z^{2} \cdot\left|\frac{\Delta M}{\Delta z}\right|=[0.4 \cdot(7 \mathrm{m})]^{2}\left|\frac{(8-5) \mathrm{m} / \mathrm{s}}{(10-4) \mathrm{m}}\right|=3.92 \mathrm{m}^{2} \mathrm{s}^{-1}\)
Next, use eq. (18.41):
FH = –K(∆θ/∆z) = –(3.92 m2 s–1)·(16–15°C)/(10–4m) = –0.65 K·ms–1
Check: Units OK. Physics OK.
Exposition: The negative sign means a downward heat flux, from hot to cold. This is typical for statically stable ABL.


