15.3: Lightning and Thunder
- Page ID
- 9626
Lightning (Fig. 15.21) is an electrical discharge (spark) between one part of a cloud and either:
- another part of the same cloud [intracloud (IC) lightning],
- a different cloud [cloud-to-cloud (CC) lightning, or intercloud lightning],
- the ground or objects touching the ground [cloud-to-ground (CG) lightning], or
- the air [cloud-to-air discharge (CA)].
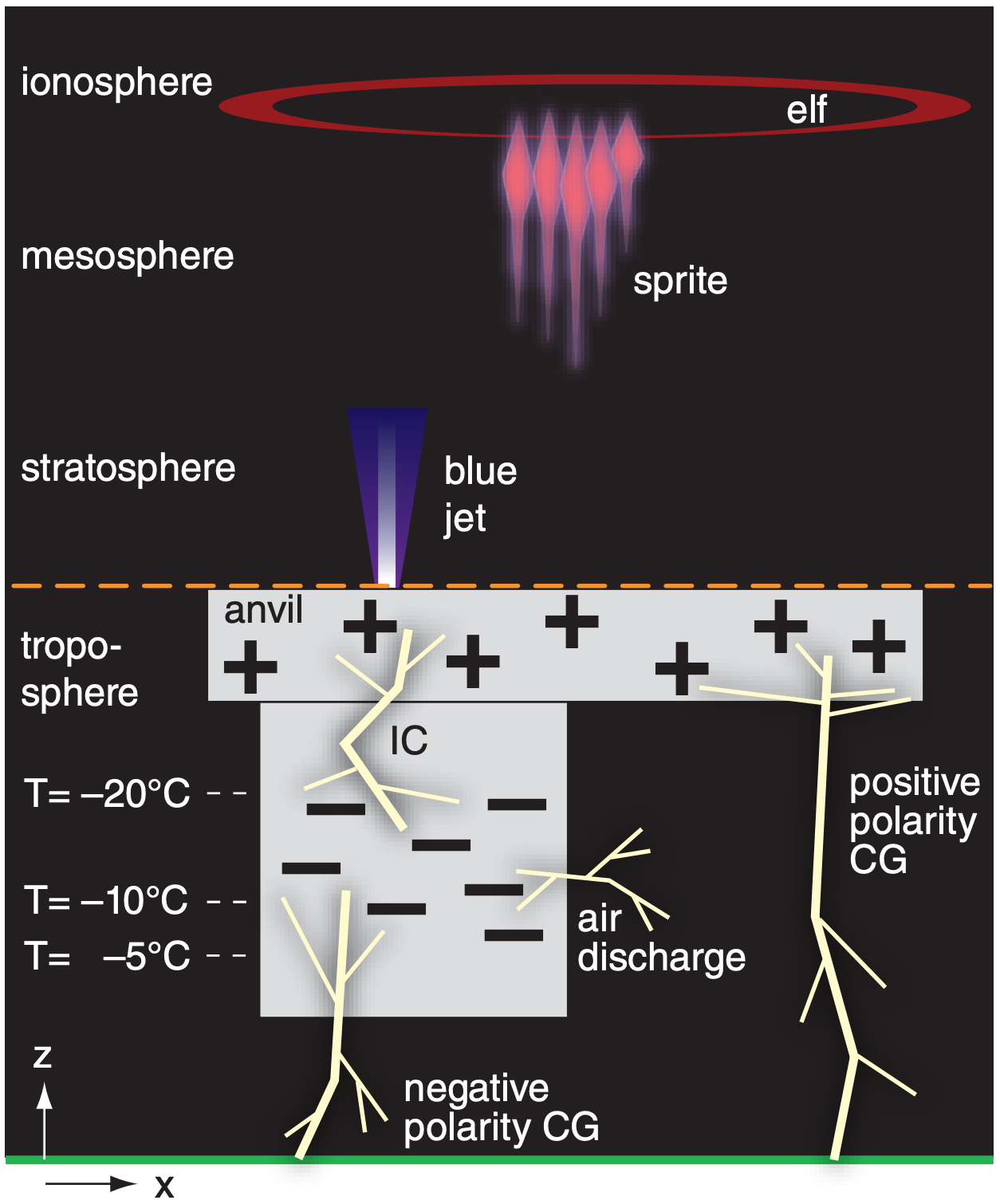
Other weak high-altitude electrical discharges (blue jets, sprites and elves) are discussed later.
The lightning discharge heats the air almost instantly to temperatures of 15,000 to 30,000 K in a lightning channel of small diameter (2 to 3 cm) but long path (0.1 to 10 km). This heating causes:
- incandescence of the air, which you see as a bright flash, and
- a pressure increase to values in the range of 1000 to 10,000 kPa in the channel, which you hear as thunder.
On average, there are about 2000 thunderstorms active at any time in the world, resulting in about 45 flashes per second. Worldwide, there are roughly 1.4x109 lightning flashes (IC + CG) per year, as detected by optical transient detectors on satellites. Africa has the greatest amount of lightning, with 50 to 80 flashes km–2 yr–1 over the Congo Basin. In North America, the region having greatest lightning frequency is the Southeast, having 20 to 30 flashes km–2 yr–1, compared to only 2 to 5 flashes km–2 yr–1 across most of southern Canada.
113 people died in 1975 when a commercial jet flew through a downburst while trying to land at J. F. Kennedy airport near New York City.
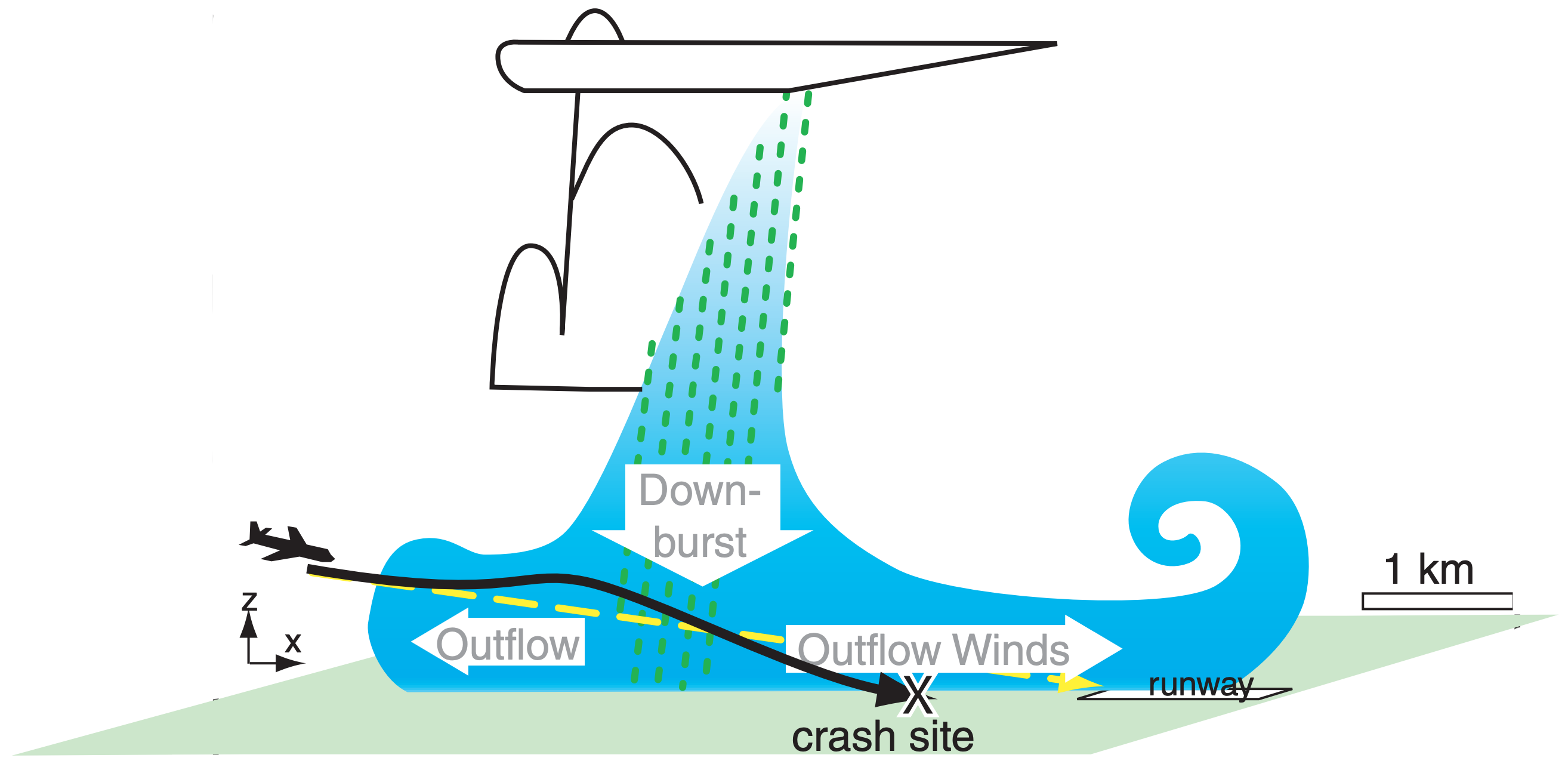
The airliner first encountered outflow headwinds while trying to gradually descend along the normal glideslope (dashed line) toward the runway. Due to the aircraft’s forward inertia, the headwinds caused more air to blow over wings, generating more lift. This extra lift caused the aircraft to unintentionally climb (or not descend as fast), as shown by the solid line representing the actual aircraft path.
To compensate, the pilot slowed the engines and pointed the aircraft more downward, to try to get back down to the desired glideslope. But then the plane flew through the downburst, pushing the aircraft downward below the glideslope. So the pilot had to compensate in the opposite direction, by throttling up the engines to full power and raising the nose of the aircraft to try to climb back up to the glideslope.
By this time, the aircraft had reached the other side of the downburst, where the outflow winds were moving in the same direction as the aircraft. Relative to the aircraft, there was less air flowing over the wings and less lift, allowing gravity to pull the aircraft down even faster. The pilot increased pitch and engine power, but the turbine engines took a few seconds to reach full power. The inertia of the heavy aircraft caused its speed to increase too slowly. The slow airspeed and downward force of the downburst caused the aircraft to crash short of the runway.
That crash motivated many meteorological field experiments to enable better detection and forecasts of downbursts and gust fronts. Airports have special equipment (anemometers and Doppler radar) to detect dangerous wind shears; air-traffic controllers have a protocol to alert pilots and direct them to safety; and pilots are trained to carry extra speed and make earlier missed-approach decisions.
On average, only 20% of all lightning strokes are CG, as measured using ground-based lightning detection networks, but the percentage varies with cloud depth and location. The fraction of lightning that is CG is less than 10% over Kansas, Nebraska, the Dakotas, Oregon, and NW California, and is about 50% over the Midwest states, the central and southern Rocky Mountains, and eastern California.
CG lightning causes the most deaths, and causes power surges or disruptions to electrical transmission lines. In North America, the southeastern states have the greatest density of CG lightning [4 to 10 flashes km–2 yr–1 ]. Tampa, Florida, has the greatest CG flash density of 14.5 flashes km–2 yr–1.
Most CG lightning causes the transfer of electrons (i.e., negative charge) from cloud to ground, and is called negative-polarity lightning. About 9% of CG lightning is positive-polarity, and usually is attached to the thunderstorm anvil (Fig. 15.21) or to the extensive stratiform region of a mesoscale convective system. Because positive-polarity lightning has a longer path (to reach between anvil and ground), it requires a greater voltage gradient. Thus, positive CG lightning often transfers more charge with greater current to the ground, with a greater chance of causing deaths and forest fires.
Electricity is associated with the movement of electrons and ions (charged particles). In metal channels such as electrical wires, it is usually only the electrons (negative charges) that move. In the atmospheric channels such as lightning, both negative and positive ions can move, although electrons can move faster because they are smaller, and carry most of the current. Lightning forms when static electricity in clouds discharges as direct current (DC).
Each electron carries one elementary negative charge. One coulomb (C) is an amount of charge (Q) equal to 6.24x1018 elementary charges. [Don’t confuse C (coulombs) with °C (degrees Celsius).] The main charging zone of a thunderstorm is between altitudes where –20 ≤ T ≤ –5°C (Fig. 15.21), where typical thunderstorms hold 10 to 100 coulombs of static charge.
The movement of 1 C of charge per 1 second (s) is a current (I) of 1 A (ampere).
\(\ \begin{align} I=\Delta Q / \Delta t\tag{ec1}\end{align}\)
The median current in lightning is 25 kA.
Most substances offer some resistance (R) to the movement of electrical charges. Resistance between two points along a wire or other conductive channel is measured in ohms (Ω).
An electromotive force (V, better known as the electrical potential difference) of 1 V (volt) is needed to push 1 A of electricity through 1 ohm of resistance.
\(\ \begin{align} V=I \cdot R\tag{ec2}\end{align}\)
[We use italicized V to represent the variable (electrical potential), and non-italicized V for its units (volts).]
The power Pe (in watts W) spent to push a current I with voltage V is
\(\ \begin{align} P_{e}=I \cdot V\tag{ec3}\end{align}\)
where 1 W = 1 V · 1 A. For example, lightning of voltage 1x109 V and current 25 kA dissipates 2.5x1013 W.
A lightning stroke might exist for ∆t = 30 µs, so the energy moved is Pe ·∆t = (2.5x1013 W)·(0.00003 s) = 7.5x108 J; namely, about 0.75 billion Joules.
15.3.1. Origin of Electric Charge
Large-scale (macroscale) cloud electrification occurs due to small scale (microphysical) interactions between individual cloud particles. Three types of particles are needed in the same volume of cloud:
- small ice crystals formed directly by deposition of vapor onto ice nuclei;
- small supercooled liquid water (cloud) droplets;
- slightly larger graupel ice particles.
An updraft is also needed to blow the small particles upward relative to the larger ones falling down.
These three conditions can occur in cumulonimbus clouds at altitudes where temperature is between 0°C and –40°C. However, most of the electrical charge generation is observed to occur at heights where the temperature ranges between –5 and –20°C (Fig. 15.21).
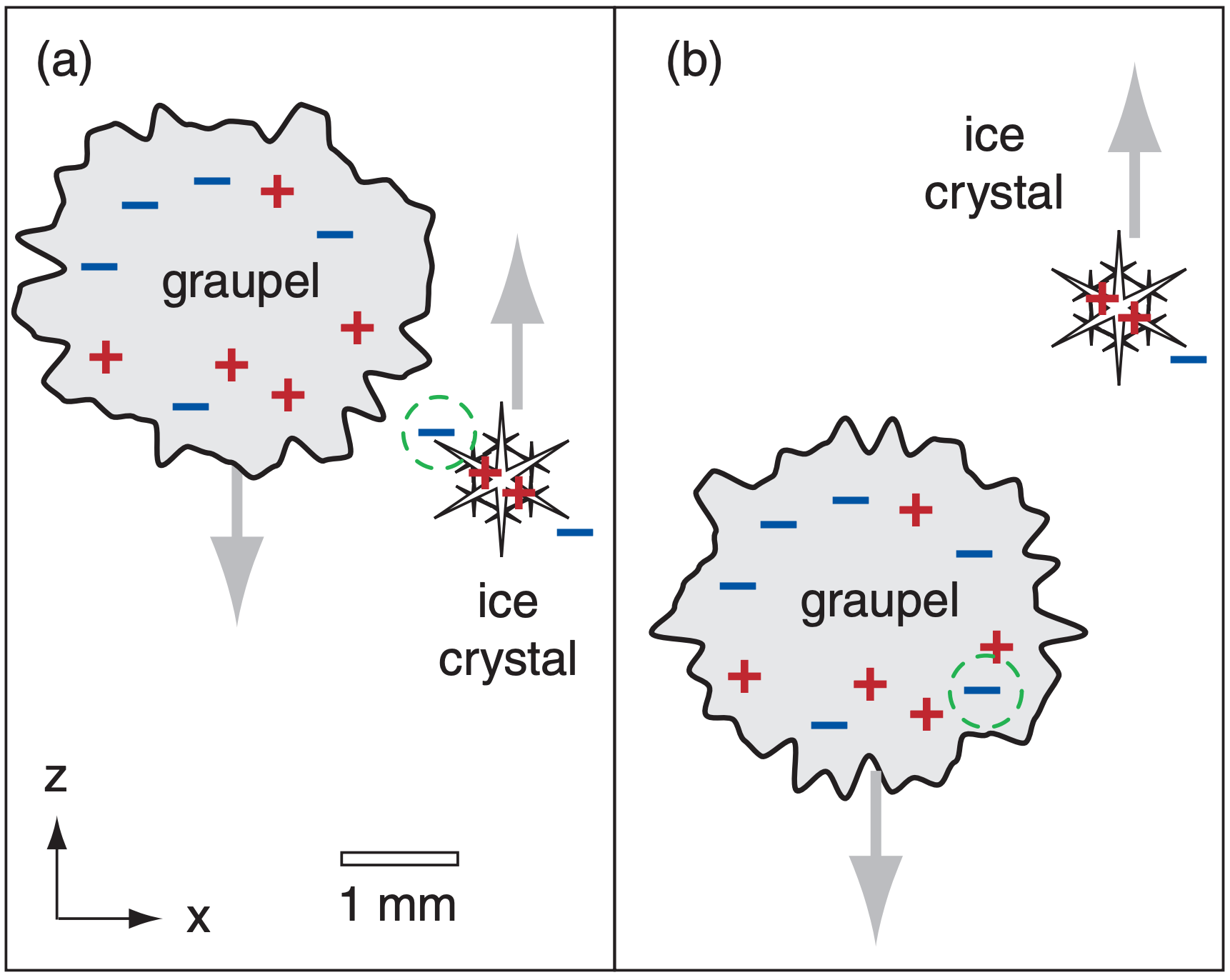
The details of how charges form are not known with certainty, but one theory is that the falling graupel particles intercept lots of supercooled cloud droplets that freeze relatively quickly as a glass. [Definitions: A glass is a state of solid material in which the molecules have random arrangement. A crystal has an ordered lattice of molecules.] Meanwhile, separate ice nuclei allow the growth of ice crystals by direct deposition of vapor. The alignment of water molecules on these two types of surfaces (glass vs. crystal) are different, causing different arrangement of electrons near the surface. Ice crystals tend to have negative charges at the tips of the crystal arms.
If one of the small ice crystals (being blown upward in the updraft because of its small terminal velocity) hits a larger graupel particle (heavier and falling downward relative to the updraft air), then about 100,000 electrons (a charge of about 1.5x10–14 C) will transfer from the small ice crystal (leaving the ice crystal positively charged) to the larger glass-surfaced graupel particle (leaving it negatively charged) during this one collision (Fig. 15.22). This is the microphysical electrification process.
In 1 km3 of thunderstorm air, there can be on the order of 5x1013 collisions of graupel and ice crystals per minute. The lighter-weight ice crystals carry their positive charge with them as they are blown in the updraft to the top of the thunderstorm, leading to the net positive charge in the anvil. Similarly, the heavier graupel carry their negative charges to the middle and bottom of the storm. The result is a macroscale (Fig. 15.21) charging rate of the thunderstorm cloud of order 1 C km–3 min–1. As these charges continue to accumulate, the electric field (i.e., voltage difference) increases between the cloud and the ground, and between the cloud and its anvil.
The electric field strength (E, which is the magnitude of the electric field or the gradient of the electric potential) measures the electromotive force (voltage V) across a distance (d), and has units of V m–1 or V km–1.
\(\ \begin{align} E=V / d\tag{ev1}\end{align}\)
Averaged over the whole atmosphere, |E| ≈ 1.3x105 V km–1 in the vertical. A device that measures electric field strength is called a field mill.
Near thunderstorms, the electric field can increase because of the charge build-up in clouds and on the ground surface, yielding electric-potential gradients (E = 1x109 to 3x109 V km–1) large enough to ionize air along a narrow channel, causing lightning. When air is ionized, electrons are pulled off of the originally neutral molecules, creating a plasma of charged positive and negative particles that is a good conductor (i.e., low resistivity).
Electrical resistivity (ρe) is the resistance (R) times the cross-section area (Area) of the substance (or other conductive path) through which electricity flows, divided by the distance (d) across which it flows, and has units of Ω·m.
\(\ \begin{align} \rho_{e}=R \cdot Area/ d\tag{ev2}\end{align}\)
Air near sea level is not a good electrical conductor, and has a resistivity of about ρe = 5x1013 Ω·m. One reason why its resistivity is not infinite is that very energetic protons (cosmic rays) enter the atmosphere from space and can cause a sparse array of paths of ionized particles that are better conductors. Above an altitude of about 30 km, the resistivity is very low due to ionization of the air by sunlight; this conductive layer (called the electrosphere) extends into the ionosphere.
Pure water has ρe = 2.5x105 Ω·m, while seawater is an even better conductor with ρe = 0.2 Ω·m due to dissolved salts.
Vertical current density (J) is the amount of electric current that flows vertically through a unit horizontal area, and has units A m–2.
\(\ \begin{align} J=I / Area\tag{ev3}\end{align}\)
In clear air, typical background current densities are 2x10–12 to 4x10–12 A m–2.
Within a volume, the electric field strength, current density, and resistivity are related by
\(\ \begin{align} E=J \cdot \rho_{e}\tag{ev4}\end{align}\)
Air is normally a good insulator in the bottom half of the troposphere. For dry air, a voltage gradient of Bdry = 3x109 V km–1 (where V is volts) is needed to ionize the air to make it conductive. For cloudy air, this breakdown potential is Bcloud = 1x109 V km–1. Ionization adds/removes electrons to/from the air molecules. If lightning (or any spark) of known length ∆z occurs, then you can use the breakdown potential to calculate the voltage difference ∆Vlightning across the lightning path:
\(\ \begin{align} \Delta V_{\text {lightning}}=B \cdot \Delta z\tag{15.16}\end{align}\)
where B is the dry-air or cloudy-air breakdown potential, depending on the path of the lightning.
Sample Application
What voltage difference is necessary to create a lightning bolt across the dry air between cloud base (at 2 km altitude) and the ground?
Find the Answer
Given: ∆z = 2 km, B = 3x109 V km–1
Find: ∆Vlightning = ? V
Use eq. (15.16): ∆Vlightning = (3x109 V km–1)·(2 km) = 6x109 V
Check: Units OK. Physics OK.
Exposition: Six billion volts can cause cardiac arrest, so it is wise to avoid being struck by lightning. High-voltage electrical transmission lines are often about 3.5x105 V. Lightning is nearly tied with floods as being the most fatal weather hazard in North America.
15.3.2. Lightning Behavior & Appearance
When sufficient charge builds up in the cloud to reach the breakdown potential, an ionized channel called a stepped leader starts to form. It steps downward from the cloud in roughly 50 m increments, each of which takes about 1 µs to form, with a pause of about 50 µs between subsequent steps (Fig. 15.23). While propagating down, it may branch into several paths. To reach from the cloud to the ground might take hundreds of steps, and take 50 ms duration. For the most common (negative polarity) lightning from the middle of the thunderstorm, this stepped leader carries about 5 C of negative charge downward.
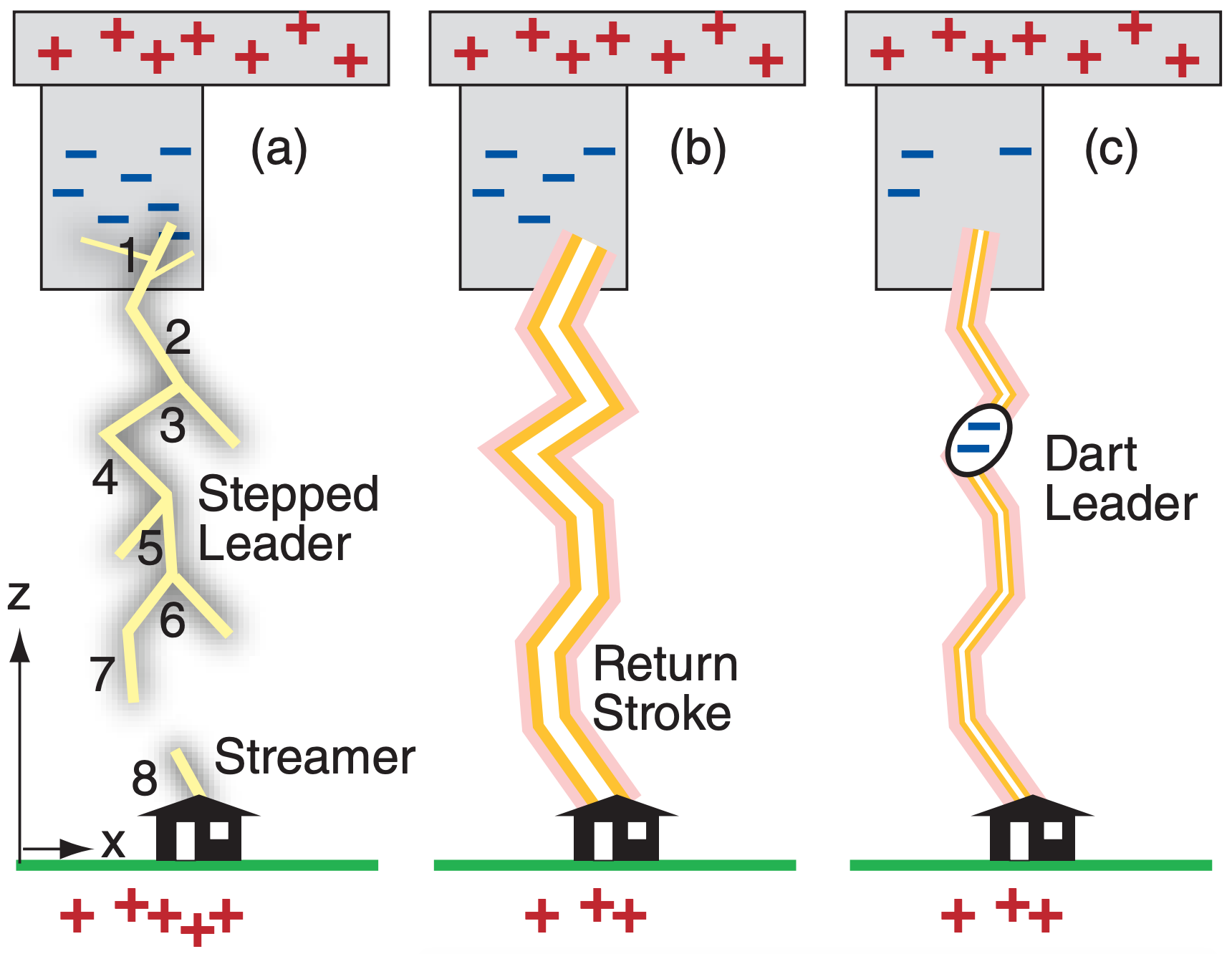
When it is within about 30 to 100 m of the ground or from the top of an object on the ground, its strong negative charge repels free electrons on the ground under it, leaving the ground strongly positively charged. This positive charge causes ground-to-air discharges called streamers, that propagate upward as very brief, faintly glowing, ionized paths from the tops of trees, poles, and tall buildings. When the top of a streamer meets the bottom of a stepped leader, the conducting path between the cloud and ground is complete, and there is a very strong (bright) return stroke from the ground to the cloud. During this return stroke, electrons drain downward first from the bottom of the stepped leader, and then drain downward from successively higher portions of the channel, producing the flash of light that you see. The stepped leader with return stroke are called a lightning stroke. A lightning strike is where a stroke hits an object.
Although thunderstorm winds and turbulence tend to rip apart the ionized channel, if the remaining negative charges in the cloud can recollect within about 20 to 50 ms, then another stroke can happen down the same conducting path. This second stroke (and subsequent strokes) forms as a dart leader carrying about 1 C of charge that moves smoothly (not in steps) down the existing channel (with no branches) to the ground, triggering another return stroke. Ten strokes can easily happen along that one ionized channel, and taken together are called a lightning flash. The multiple return strokes are what makes a lightning flash appear to flicker.
In Canada, 99% of CG strokes have currents less than 100 kA. Summer large-current flashes with negative polarity can have 10 or more strokes, and occur mostly in western Canada. First-stroke peak currents are strongest in winter and in northern Canada.
Positive polarity is observed in about 11% of the CG flashes in E. Canada, and about 17% of the CG flashes in W. Canada. In British Columbia and Yukon about 25% of the CG flashes have positive polarity.
In W. Canada, 89% of the positive CG lightning flashes had only one stroke, while 48% of the negative CG lightning had only one stroke. The average number of strokes per CG flash is 2 to 2.4 for negative polarity CG flashes, and about 1 stroke for positive CG.
IC and CG lightning can have different appearances that are sometimes given colloquial names. Anvil crawlers or spider lightning is IC lightning that propagates with many paths (like spider legs) along the underside of anvils or along the bottom of the stratiform portion of mesoscale convective systems. Some spider lightning is exceptionally long, exceeding 100 km path lengths.
If an IC lightning channel is completely hidden inside a cloud, then often observers on the ground see the whole cloud illuminated as the interior light scatters off the cloud drops (similar to the light emitted from a frosted incandescent light bulb where you cannot see the filament). This is called sheet lightning. Lightning from distant thunderstorms may illuminate hazy cloud-free sky overhead, causing dim flashing sky glow called heat lightning in the warm, prestorm environment.
A bolt from the blue is a form of CG anvil lightning that comes out laterally from the side of a storm, and can travel up to 16 km horizontally into clear air before descending to the ground. To people near where this lightning strikes, it looks like it comes from clear blue sky (if they cannot see the thunderstorm that caused it).
Ball lightning is difficult to study, but has been observed frequently enough to be recognized as a real phenomenon. It is rare, but seems to be caused by a normal CG strike that creates a longer lasting (many seconds to minutes) glowing, hissing plasma sphere that floats in the air and moves.
After the last return stroke of CG lightning, the rapidly dimming lightning channel sometimes exhibits a string of bright spots that don’t dim as fast as the rest of the channel, and thus appear as a string of glowing beads, called bead lightning.
When CG multiple return strokes happen along a lightning channel that is blowing horizontally in the wind, the human eye might perceive the flash as a single broad ribbon of light called ribbon lightning. Lightning with a very brief, single return stroke is called staccato lightning.
Above the top of strong thunderstorms can be very brief, faint, electrical discharges that are difficult to see from the ground, but easier to see from space or a high-flying aircraft (Fig. 15.21). A blue jet is a vertical anvil-to-air discharge into the stratosphere. Red sprites can spread between cloud top and about 90 km altitude (in the mesosphere), and have diameters of order 40 km. Elves are extremely faint glowing horizontal rings of light at 90 km altitude with radii that increase at the speed of light, centered above strong lightning strokes in thunderstorms. Most people never see these.
More chase guidelines from Charles Doswell III (continued from the previous chapter):
The #2 Threat: Lightning
- Stay inside your car if cloud-to-ground (CG) lightning is less than 1 mile away.
- CG threat is high when rain first reaches you.
- CG can strike well away from the storm. Move to safety. If you can’t, then:
- Avoid being the tallest object around.
- Don’t stand close to fences or power poles that are connected to wires going closer to the storm.
- Make yourself low (i.e., squat), but don’t lay, sit, or kneel on the ground, and don’t have your hands touching anything connected to the ground.
- You might not have any warning signs (hear thunder, hear hissing or crackling discharges of electricity nearby, or feel your hair stand on end) before you are struck.
- You and your chase-team members should be trained on how to do CPR (cardiopulmonary resuscitation), and should not be afraid to use it immediately if appropriate.
- Non-metalic camera tripods and insulated shoes don’t reduce your threat of being struck by lightning.
(continues later in this chapter)
The initial high temperature and pressure inside the lightning channel cause the oxygen in the air to react with the other gases.
Nitrogen, which makes up 78% of the atmosphere (see Chapter 1), oxidizes inside the ionized lightning path to become various oxides of nitrogen (NOx). During rainout, the NOx can fall as acid rain (nitric acid), which hurts the plants and acidifies streams and lakes on the short term. But over the long term, the NOx rained out can help fertilize the soil to encourage plant growth.
Even the oxygen molecules (O2) can be oxidized within the lightning channel to become ozone (O3), which we smell in the air as a sharp or fresh odor. Sometimes this odor is carried down and out from the thunderstorm by the downburst and outflow winds, which we can smell when the gust front passes just before the thunderstorm arrives.
Because of all this oxidation, we can say that lightning causes the air to burn.
15.3.3. Lightning Detection
During a lightning stroke, the changing flow of electricity along the lightning channel creates and broadcasts electromagnetic waves called sferics. A broad range of frequencies is transmitted, including radio waves that you hear as static or snaps on AM radio. Detectors on the ground receive these radio signals and accurately measure their strength and time of arrival. Other types of lightning sensors are based on magnetic direction finders.
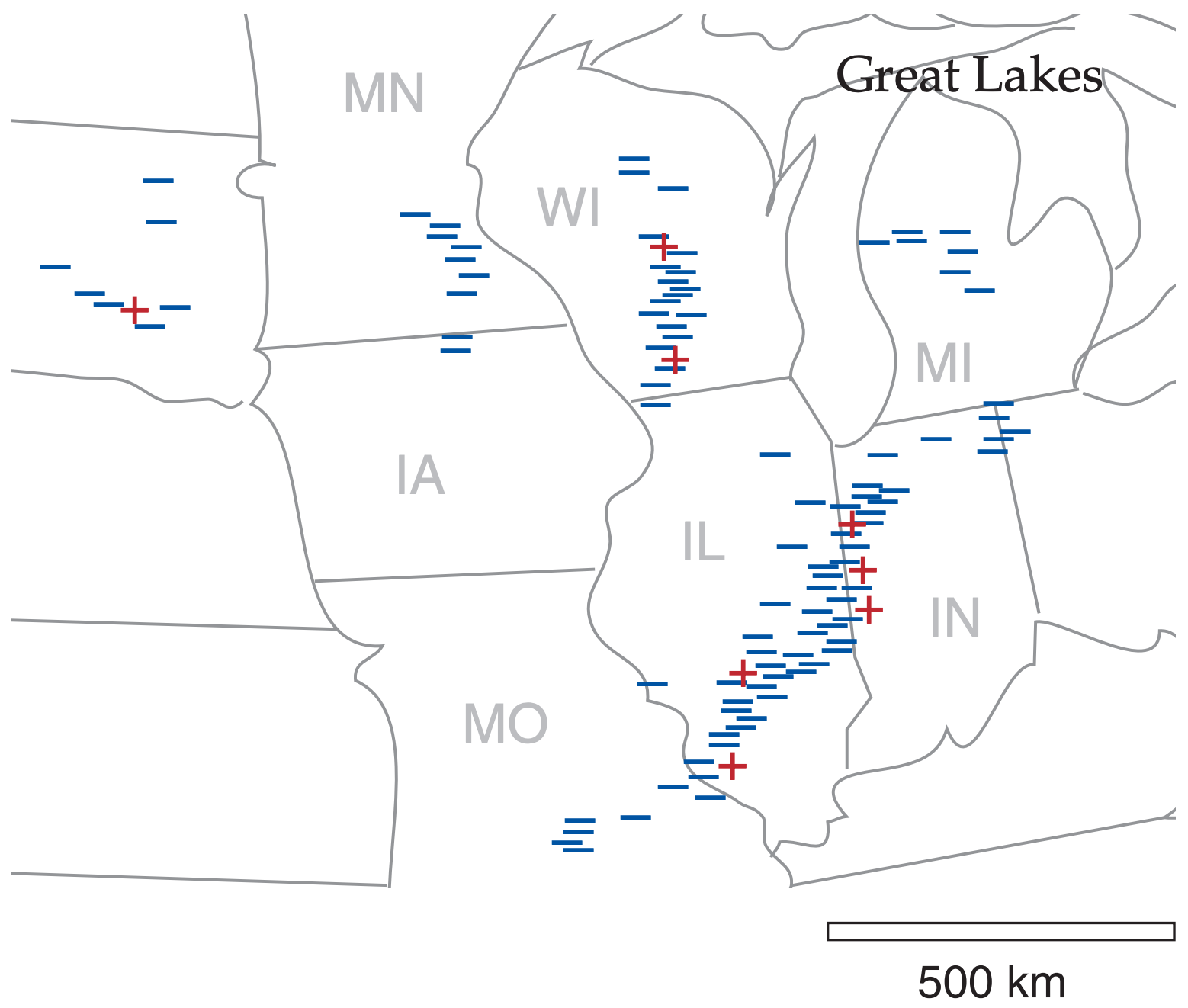
To pinpoint the location of each lightning strike, a continent-wide array of ground stations observe signals from the same lightning discharge. These ground stations either have direction-finding capability or relative time-of-arrival capability (to infer the range of the strike from the station). Regardless of the station capabilities, the strike is located by triangulating directions or ranges from all the stations that received the signal. All the strike locations during a time interval (5 minutes to a hour) are then plotted on a map (Fig. 15.24). Such an array of detectors on the Earth’s surface and associated communication and computer equipment is called a lightning detection network (LDN).
Sample Application
A lightning stroke of max intensity 10 kA occurs 100 km from a detection station. The station would likely measure what electric field value?
Find the Answer
Given: D = 100 km, Imax = 10 kA,
Find: E = ? V m–1
Assume: vL = 1.5 x 108 m s–1
Rearrange eq. (15.17) to solve for E:
\(E=\left[-v_{L} /\left(2 \pi \cdot \varepsilon_{o} c^{2}\right)\right] \cdot\left(I_{\max } / D\right)\)
E =[ (– 1.5 x 108 m s–1) / (2π· (8.854 x 10–12 A·s·(V·m)–1 )· (3.00986 x 108 m s–1)2)] · [(10 kA)/100 km)] · = – 2.98 V m–1
Check: Physics and units are OK.
Lightning current flows from high to low voltage (i.e., it flows opposite to the voltage gradient), which is why the answer has a negative sign.
Exposition: Lightning can have positive or negative polarity (i.e., the charge that goes down to the ground). LDN detectors can measure this as well as the waveform of the lightning signal, and are thus able to discriminate between CG and cloud-to-cloud lightning. The net result is that LDNs can provide much valuable information to utility companies and forest fire fighters, including lightning intensity, location, polarity, and type (CG or other).
Some of the sferics are generated at very low frequencies (VLF). Some LDN systems measure these VLF at a frequency of about 10 kHz (wavelength ≈ 30 km). The advantage of these VLF waves is that they can travel large distances — trapped in a waveguide between the ionosphere and the ground.
When a VLF wave from lightning passes over an LDN ground station, it modulates the electric field near the station (see the INFO on “Electricity in a Volume”). When multiple stations measure the same wave, the distance D (m) between the lightning and the stations can be estimated, and the peak electric field E (V m–1) measured at any one station can be used to find the approximate peak current Imax (A) flowing in the lightning return stroke:
\(\ \begin{align} I_{\max }=-2 \pi \cdot \varepsilon_{o} \cdot c^{2} \cdot E \cdot D / v_{L}\tag{15.17}\end{align}\)
where εo = 8.854 x 10–12 A·s·(V·m)–1 is the permittivity of free space, c = 3.00986 x 108 m s–1 is the speed of light, and vL = 1.0 to 2.2 x 108 m s–1 is the return-stroke current velocity.
The USA has a National Lightning Detection Network (NLDN) that typically detects more than 20 million CG flashes per year. Peak electrical currents as high as 400 kA have been rarely observed, but the median peak current is about 25 kA. The average duration of a lightning stroke is about 30 µs, and the average peak power per stroke is about 1012 W. One to ten return strokes (with 50 - 300 ms pauses between strokes) can occur in the same ionized path before winds break the path apart.
Satellite systems also detect lightning. Low-lightlevel video and digital cameras have been on board some satellites and manned space vehicles, and have observed lightning at night from the flashes of light produced. An optical transient detector (OTD) has also been deployed that measures the changes in light leaving the portion of atmosphere viewed.
15.3.4. Lightning Forecasting
A dimensionless Cloud Physics Thunder Parameter (CPTP) is defined as:
\(\ \begin{align} \mathrm{CPTP}=\left(T_{o}-T_{E I}\right) \cdot\left(C_{-20}-C_{r}\right) /\left(T_{r} \cdot C_{r}\right)\tag{15.18}\end{align}\)
where To = –19°C is an offset temperature, TEL is environmental temperature (°C) at the thunderstorm equilibrium level, Tr = 1°C is a reference temperature, C–20 is the portion of MUCAPE between altitudes where environmental temperatures are 0 and –20°C, and Cr = 100 J kg–1 is a reference CAPE value. But CPTP is set to 0 if TLCL ≤ –10°C. Lightning in thunderstorms is likely when CPTP ≥ 1.
Sample Application
Suppose the environmental sounding is the same as shown in Fig. 15.7, but where C–20 = 1100 J kg–1 is the portion of MUCAPE between altitudes where the environmental sounding is between 0 and –20°C. Is lightning likely?
Find the Answer
Given: C–20 = 1100 J kg–1
Find: CPTP = ? °C to determine lightning likelihood.
Inspection of Fig. 15.7 gives TEL ≈ –40°C and TLCL = 11°C.
Since TLCL > –10°C, CPTP is not set to zero. Therefore we must compute it using eq. (15.18):
CPTP = [–19 –(–40)]°C · [(1100 – 100)J/kg)] / [1°C · 100 J/kg] = 210 (dimensionless)
Since CPTP ≥ 1, we conclude that lightning is likely if thunderstorms occur.
Check: Physics and units are OK.
Exposition: Caution: if no thunderstorm occurs, then CPTP is irrelevant. So prediction of lightning also requires prediction of deep convection (CB clouds).
The definition of CPTP is based on the basic ingredients for CB electrification: supercooled liquid water (ensured by TLCL > –10°C); vertical motion in the 0 to –20°C storm region where charge separation occurs (ensured by sufficiently large MUCAPE); and cloud top above the charge-separation region (ensured by TEL ≤ –20°C).
15.3.5. Lightning Hazards and Safety
When lightning strikes electric power lines it can cause power surges (transient spikes in voltage and current in the line). Power surges can ignite electric transformers on power poles, trip circuit breakers and fuses, fry electronics, and electrocute people touching wired appliances.
Based on observations of many such surges, the probability Prob that surge current will be greater than I (kA) in the power line is:
\(\ \begin{align} \operatorname{Prob}=\exp \left\{-0.5 \cdot\left[\frac{\ln \left(\left(I+I_{0}\right) / I_{1}\right)}{s_{1}}\right]^{2}\right\}\tag{15.19}\end{align}\)
for I ≥ ( I1 – Io ), where the empirical probability-distribution parameters are Io = 2 kA, I1 = 3.5 kA, and s1 = 1.5. This curve is plotted in Fig. 15.25 — showing that 50% of the these surges exceed about 20 kA.
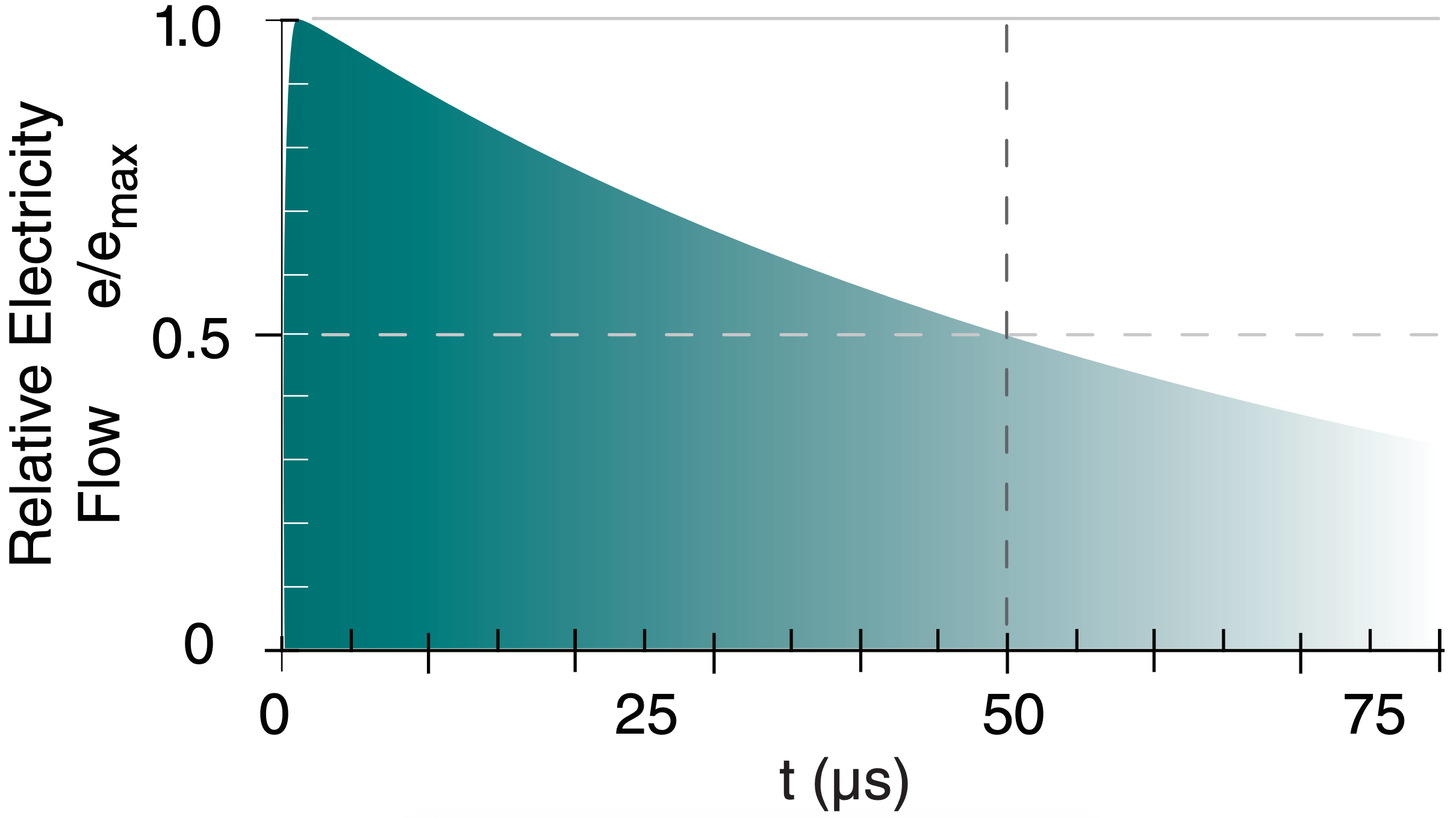
When a lightning-created surge travels down an electric power line, the voltage (and current) e at any point rapidly increases to its peak value emax and then slowly decays. Electrical engineers approximate this by:
\(\ \begin{align} e=e_{\max } \cdot a \cdot\left[\exp \left(-\frac{t}{\tau_{1}}\right)-\exp \left(-\frac{t}{\tau_{2}}\right)\right]\tag{15.20}\end{align}\)
The nominal constants are: \(\ \tau_1\) = 70 µs, \(\ \tau_2\) = 0.15 µs, and a = 1.014. Fig. 15.26 shows a surge that reaches its peak in 1 µs, and by 50 µs has decayed to half.

When lightning strikes sandy ground, it can melt and fuse the sand along its path into a long narrow glassy tube called a fulgurite. When it strikes trees and flows down the trunk to the ground, it can cause the moisture and sap in the tree to instantly boil, causing the bark to splinter and explode outward as lethal wooden shrapnel. Sometimes the tree trunk will split, or the tree will ignite.
The electrons flowing in lightning all have a negative charge and try to repel each other. While moving along the narrow lightning channel, the electrons are constrained to be close together. However, if the lightning hits a metal-skinned airplane, the electrons push away from each other so as to flow along the outside surfaces of the airplane, thus protecting the people inside. Such a Faraday cage effect also applies to metal-skinned cars. Other than the surprisingly loud noise and bright lightning flash, you are well protected if you don’t touch any metal. Where the lightning attaches to the car or aircraft, a pinhole can be burned through the metal.
Dangerous activities/locations associated with lightning strikes are:
- Open fields including sports fields.
- Boating, fishing, and swimming.
- Using heavy farm or road equipment.
- Playing golf.
- Holding a hard-wired telephone.
- Repairing or using electrical appliances.
You should take precautions to avoid being struck by lightning. Avoid water and metal objects. Get off of high ground. Avoid open fields. Stay away from solitary trees or poles or towers (which might attract lightning). Go indoors or inside a metal-skinned car, van or truck if lightning is within 10 km (i.e., 30 seconds or less between when you see a lightning flash and when you hear its thunder). Even if you don’t see lightning or hear thunder, if the hair on your head, neck or arms stands on end, immediately go inside a building or car. If indoors, avoid using hard-wired phones, hair driers, or other appliances, and avoid touching metal plumbing or water in your sink, shower, or tub.
If you are outside and no shelter is available, crouch down immediately in the lowest possible spot with your feet together and your hands over your ears. Do not lie down, because once lightning strikes the ground or a tree, it often spreads out along the surface of the ground and can still hit you. To prevent lightning from going through your heart, do not put your hands on the ground.
If people near you are struck by lightning and fall down, do not assume they are dead. Lighting can cause a person to stop breathing or stop their heart, but they can often be revived. If a person isn’t breathing, try performing mouth-to-mouth resuscitation. If a person has no pulse, and if you have the training, do cardiopulmonary resuscitation (CPR).
Sample Application
If lightning strikes a power line, what is the probability that the surge current will be 60 kA or greater? When will this surge decay to 5 kA?
Find the Answer
Given: I = 60 kA and I/Imax = 5/60 = 0.0833
Find: Prob = ? %, t = ? µs after the surge starts
Use eq. (15.18):
\(\begin{aligned} \text {Prob} &=\exp \left\{-0.5 \cdot\left[\frac{\ln ((60+2 \mathrm{kA}) /(3.5 \mathrm{kA}))}{1.5}\right]^{2}\right\} =\exp (-1.8)=\underline{\mathbf{1 6} \%} \end{aligned}\)
Use I/Imax in place of e/emax in eq. (15.20). As time increases, the last exponential becomes small relative to the first exponential, and can be neglected. Use eq. (15.20) without the last exponential and solve it for time:
\(t=-\tau_{1} \cdot \ln \left[(1 / a) \cdot e / e_{\max }\right]=-\tau_{1} \cdot \ln \left[(1 / a) \cdot I / I_{\max }\right]\)
\(=-(70 \mu \mathrm{s}) \cdot \ln [(1 / 1.014) \cdot 0.0833]=\underline{\mathbf{175 . \mu s}}\)
Check: Agrees with Figs 15.25 & 15.26. Physics & units OK.
Exposition: The brief intense power surge can open circuit breakers, blow fuses, and melt electric power transformers. The resulting disruption of power distribution to businesses and homes can cause computers to malfunction, files to be lost, and peripherals to be destroyed.
For the non-storm-chaser, use the 30-30 Rule of lightning safety: If you are outdoors and the time between the lightning flash and thunder is 30 s or less, then seek shelter immediately. Wait 30 minutes after hearing the last thunder clap before going outdoors.
Cardiac arrest (stopped heart) is the main cause of death from a lightning strike. Surprisingly, there is usually very little burning of the skin. Other immediate effects include tinnitus (ringing in the ears due to the loud thunder), blindness, amnesia, confusion, cardiac arrhythmias, and vascular instability. Later problems include sleep disturbances, anxiety attacks, peripheral nerve damage, pain syndromes, fear of storms, personality changes, irritability, short-term memory difficulties, and depression. Lightning injures 800 to 1000 people per year in the USA, and kills 75 to 150 people per year. Support groups exist for lightning survivors.
15.3.6. Thunder
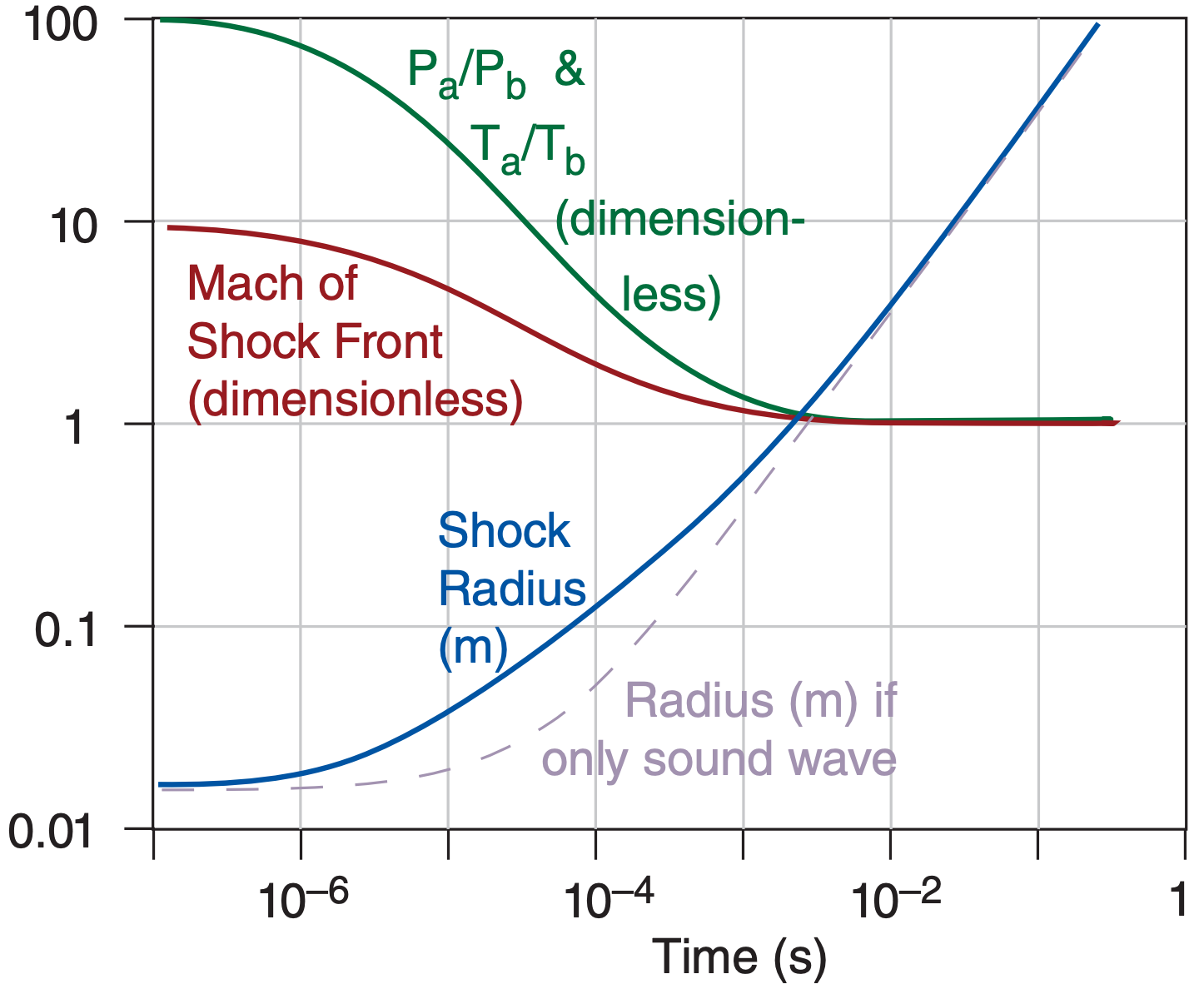
When lightning heats the air to T = 15,000 to 30,000 K, it instantly increases the air pressure to P = 1,000 to 10,000 kPa along the ionized lightning path, creating a shock front that moves at supersonic speeds up to ten times the speed of sound (i.e., Ma = 10, where Ma is Mach number). By 7 µs later, the supersonic shock-front speed has decreased to Mach 5, and has spread only about 1.5 cm from the edge of the lightning channel (Fig. 15.27). By 0.01 s after the lightning, the shock front has spread about 4 m in all directions around the lightning, and has a speed (Ma = 1.008) that is almost equal to the speed of sound (Ma = 1). Namely, it becomes a sound wave that continues to spread at the speed of sound, which you hear as thunder. So to understand thunder, we will study shock fronts first, and then sound.
One time when I was driving, lightning struck immediately next to my car. The shock wave instantly pushed the car into the next lane, without breaking any windows or causing damage. I was amazed at the power of the shock wave, and happy to be alive. - R. Stull
15.3.6.1. Shock Front
A shock front in air is created by a pressure discontinuity or pressure step. The thickness of this pressure step is only a few micrometers. This shock front advances supersonically at speed C through the air toward the lower pressure. It is NOT like a piston that pushes against the ambient air in front of it. Instead it moves THROUGH the background low-pressure air, modifies the thermodynamic and dynamic state of the air molecules it overtakes, and leaves them behind as the front continues on. This modification of the air is irreversible, and causes entropy to increase.
To analyze the shock, picture an idealized vertical lightning channel (Fig. 15.28) of radius ro. Assume the background air is calm (relative to the speed of the shock) and of uniform thermodynamic state. For simplicity, assume that air is an ideal gas, which is a bad assumption for the temperatures and pressures inside the lightning channel.
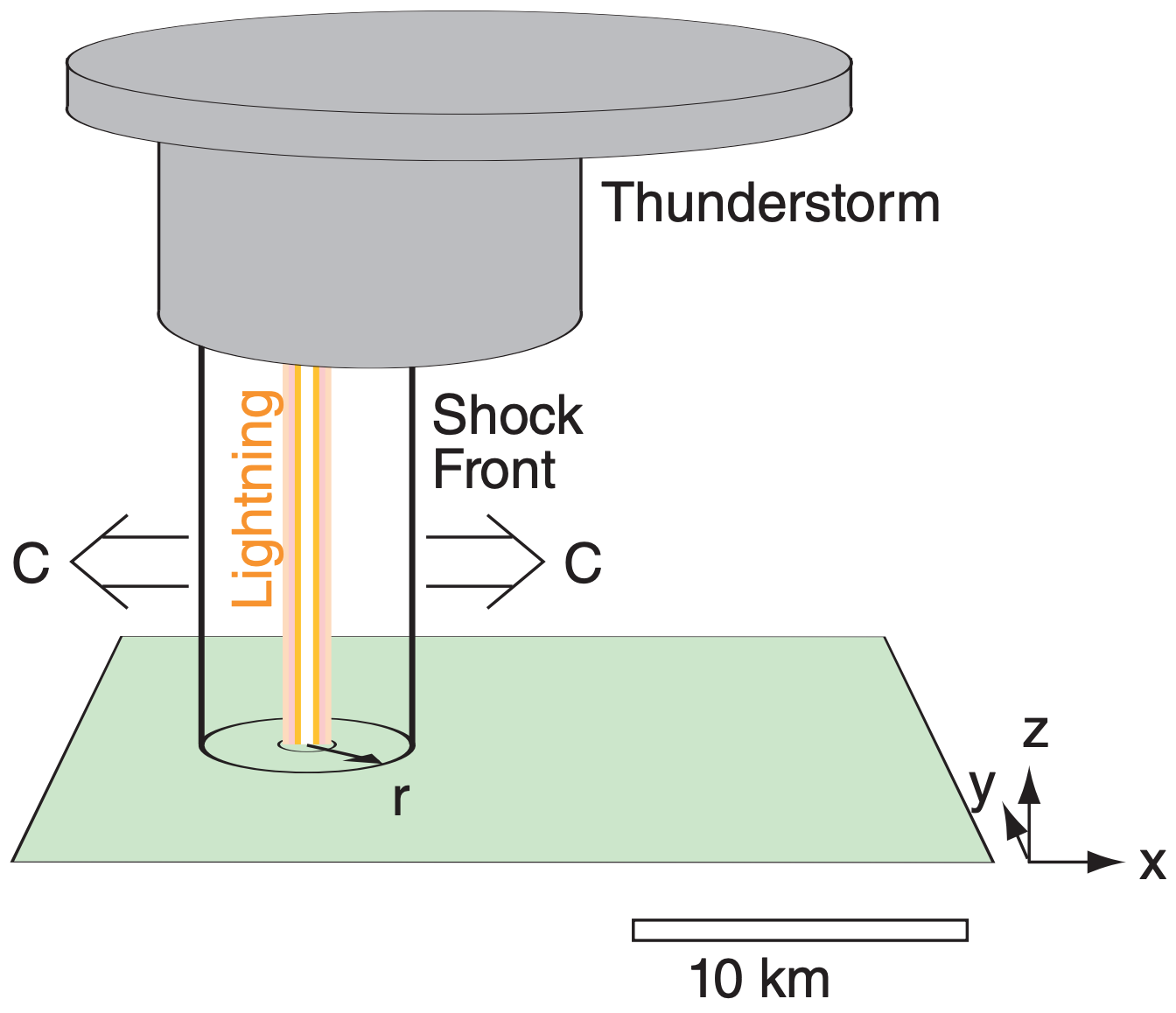
Because the shock front will expand as a cylinder of radius r around the axis of the lightning channel, ignore the vertical (because there is no net change in the vertical), and use the circular symmetry to treat this as a 1-D normal-shock problem in the horizontal. Namely, the movement of the shock front across the air molecules is perpendicular to the face of the shock front.
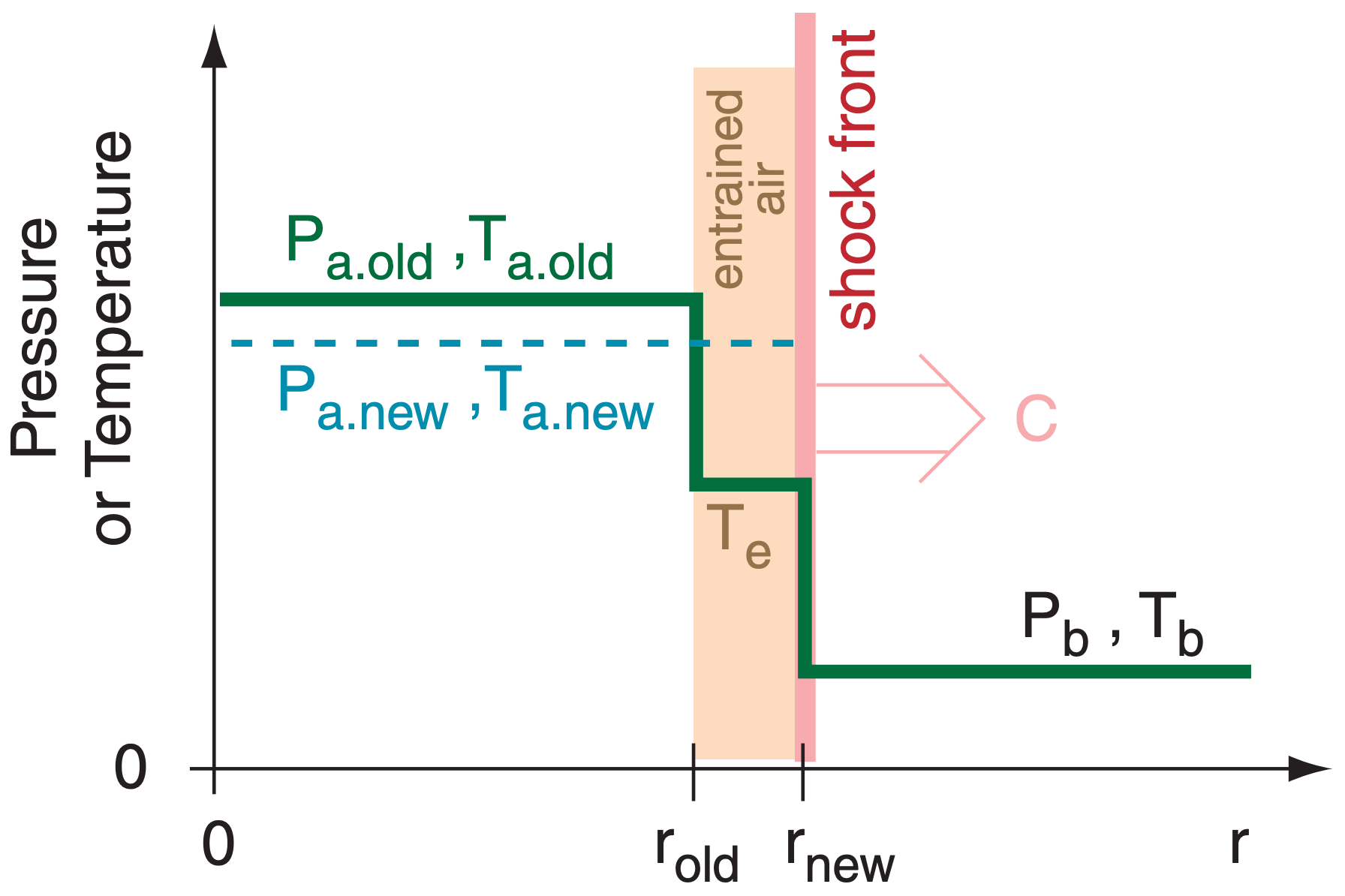
Use subscript b to indicate background air (not yet reached by the shock), and subscript e to indicate entrained air (namely, background air that has been modified by the shock-front passage). For simplicity, assume that the entrained air instantly mixes with the rest of the air inside the shock-front circle, and use subscript a to indicate the resulting average conditions inside that circle (Fig. 15.29).
For a normal-shock, the Mach number (dimensionless) of the shock wave expanding into the background air is
\(\ \begin{align} M a=\left[\frac{\left(P_{a} / P_{b}\right) \cdot(k-1)+k-1}{2 k}\right]^{1 / 2}\tag{15.21a}\end{align}\)
where P is pressure, and k = Cp/Cv . For air, k = 1.40, allowing the previous equation to be simplified to:
\(\ \begin{align} M a=\left[\frac{\left(P_{a} / P_{b}\right) \cdot 6+1}{7}\right]^{1 / 2}\tag{15.21b}\end{align}\)
One equation for the speed of sound (s) in air is
\(\ \begin{align} s=(k \cdot \Re \cdot T)^{1 / 2}\tag{15.22}\end{align}\)
where ℜ = Cp – Cv = 287 m2 s–2 K–1 is the gas constant, and T is absolute air temperature. For background air, this simplifies to
\(\ \begin{align} s_{b}=a_{s} \cdot\left(T_{b}\right)^{1 / 2}\tag{15.23}\end{align}\)
where as = 20 (m s–1)·K–1/2 is a constant for air, and Tb is background air temperature (in Kelvin). For example, if the background air has temperature 27°C (= 300 K), then the speed of sound is sb = 346.41 m s–1.
By definition, the Mach number is the speed of the object (or the shock) divided by sound speed. Thus the speed C of the shock front through the calm background air is
\(\ \begin{align} C=M a \cdot s_{b}\tag{15.24}\end{align}\)
During a small time interval ∆t, the radius r of the shock circle expands as:
\(\ \begin{align} r_{n e w}=r_{o l d}+C \cdot \Delta t\tag{15.25}\end{align}\)
The thin layer of air immediately behind the shock front is warmed (due to compression) to:
\(\ \begin{align} T_{e}=T_{b} \cdot \frac{\left[2+(k-1) \cdot M a^{2}\right]\left[2 k \cdot M a^{2}-k+1\right]}{(k+1)^{2} M a^{2}}\tag{15.26}\end{align}\)
or
\(\ \begin{align} T_{e}=T_{b} \cdot \frac{\left[5+M a^{2}\right]\left[7 M a^{2}-1\right]}{36 M a^{2}}\tag{15.27}\end{align}\)
where Tb is background air temperature and Ma is the Mach number of the shock front. Te is the temperature of the air entrained inside the shock circle.
By keeping track of the average temperature Ta of all air enclosed by the shock circle, you can use geometry to find how that average changes as the entrained air is added
\(\ \begin{align} T_{\text {a.new}}=T_{e}+\frac{\left(T_{\text {a.old}}-T_{e}\right)}{\left(r_{\text {new}} / r_{\text {old}}\right)^{2}}\tag{15.28}\end{align}\)
Lightning-formed shocks are quite different from shocks caused by chemical explosives (i.e., bombs). Conventional bombs explosively release large amounts of gas via chemical reactions, which increases the pressure, temperature, and density of the atmosphere by quickly adding gas molecules that were not there before. As the resulting shock front expands, there is a net out-rush of gas behind the shock as the gas density decreases toward background values.
Lightning, however, is a constant density (isopycnal) process, because no extra air molecules are added to the lightning channel. Namely, lightning starts with existing background air molecules and energizes whichever ones happen to be within the ionized channel. Furthermore, just outside the shock front nothing has changed in the background air (i.e., no density changes, and no movement of molecules toward or away from the shock front).
Therefore, by mass conservation, the average density ρa of air enclosed by the shock front is also constant and equal to the original (pre-lightning) background value ρb:
\(\ \begin{align} \rho_{a}=\rho_{b}= constant =P_{b} / \Re \cdot T_{b}\tag{15.29}\end{align}\)
using the ideal gas law with Pb as background air pressure, and Tb as background air temperature (in Kelvin). Immediately behind the shock front, the entrained air has higher density and pressure, but this is compensated by lower-density lower-pressure air closer to the lightning axis, resulting in constant average density as shown above.
Finally, the average pressure Pa of all air enclosed by the shock circle is found using the ideal gas law with constant density:
\(\ \begin{align} P_{a} / P_{b}=T_{a} / T_{b}\tag{15.30}\end{align}\)
where Ta = Ta.new . Equations (15.21) through (15.30) can be solved iteratively to find how conditions change as the shock evolves. Namely, Pa can be used back in eq. (15.21), and the calculations repeated. This assumes that the background thermodynamic state Tb and Pb of the undisturbed air is known.
To iterate, you need the initial conditions. Start with rold = radius of the ionized lightning channel, although there is evidence that the incandescent region of air is about 10 to 20 times larger radius than this (so you could try starting with this larger value). Because of the isopycnal nature of lightning, if you know the initial lightning temperature Ta in Kelvin, you can use eq. (15.30) to find the initial pressure ratio Pa/Pb, as sketched in Fig. 15.30.
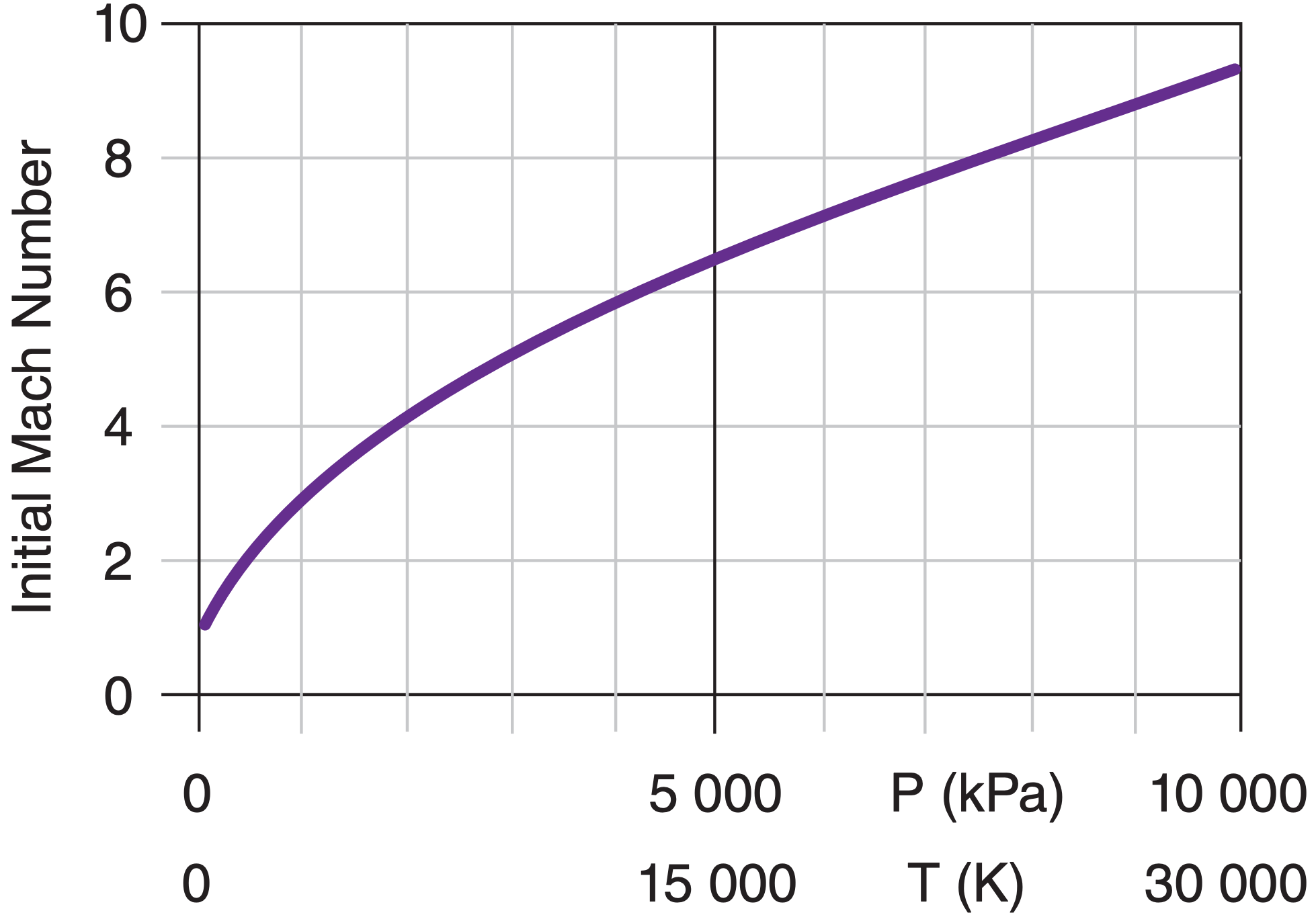
An iterative approach is demonstrated in a Sample Application, the results from which were used to create Fig. 15.27. The background air state was Tb = 300K and Pb = 100 kPa, giving ρb = 1.1614 kg m–3. For the lightning, I used initial conditions of rold = 1.5 cm = 0.015 m, Ta.old = 30,000 K, Pa = 10,000 kPa.
Anyone who has been very close (within 1 m or less) of a lightning strike (but not actually hit by the lightning itself) feels a tremendous force that can instantly throw your body (or your car if you are driving) many meters horizontally (as well as rupturing your ear drums). This is the combined effect of the pressure difference across the shock front as it passes your body or your car, and the dynamic effect of a supersonic wind in the thin layer of entrained air immediately behind the shock front.
Assuming a normal shock, the extremely brief, outward-directed wind Me in the entrained air immediately behind the shock is:
\(\ \begin{align} M_{e}=C-\left[C^{2}-2 \cdot C_{p} \cdot\left(T_{e}-T_{b}\right)\right]^{1 / 2}\tag{15.31}\end{align}\)
where Cp = 1005 m2 s–2 K–1 is the specific heat of air at constant pressure. Although initially very fast, these winds are slower than the speed of the shock front. Initial supersonic post-shock winds are about 2500 m s–1 while the shock radius is still small (1.5 cm), but they quickly diminish to subsonic values of about 10 m s–1 as the shock front expands past 2 m radius.
The resulting sequence of winds at any point not on the lightning axis is: (1) no lightning-created winds prior to shock front passage; (2) near instantaneous increase in outward-directed winds Me immediately after the shock front passes; which is quickly followed by (3) weaker inward-directed winds (never supersonic) drawn back toward the lower pressure along the lightning axis in order to conserve mass. A similar sequence of events has been observed with shock fronts from atmospheric nuclear-bomb explosions just above ground.
Sample Application
Background atmospheric conditions are Pb = 100 kPa, Tb = 300 K, and calm winds. If lightning heats the air in the lightning channel to 15,000 K, what is the initial speed of the shock front, and the initial speed of the air behind the shock front?
Find the Answer
Given: Pb = 100 kPa, Tb = 300 K, Mb = 0 m s–1. Ta = 15,000 K
Find: C = ? m s–1 , Me = ? m s–1
The shock speed equation requires the Mach speed and the speed of sound, which must be calculated first. Mach speed, in turn, depends on the initial pressure ratio. Use eq. (15.30) to find the pressure ratio:
Pa/Pb = Ta/Tb = (15000 K)/(300 K) = 50
Next, use eq (15.21) to find the Mach speed of the shock front through the background air:
Ma = {[(50)·6 + 1 ]/ 7}1/2 = 6.56
The background speed of sound from eq. (15.23) is:
sb = [20 (m s–1)·K–1/2] · (300 K)1/2 = 346.4 m s–1
Thus, using eq. (15.24):
C = 6.56 · (346.4 m s–1) = 2,271.6 m s–1
The equation for wind speed behind the shock requires the temperature behind the shock. Use eq. (15.27):
Te = (300 K)· { [5 + 6.562]·[7· 6.562 – 1] / (36 · 6.562) } = (300 K)·{ 48 · 300 / 1548 } = 2791 K
Finally, using eq. (15.31):
Me = (2,271.6 m s–1) – [ (2,271.6 m s–1)2 – 2·(1005 m2 s–2 K–1)·( 2791K – 300 K) ]1/2 = 2,271.6 – 392.3 m s–1 = 1,879.3 m s–1
Check: Units OK. Physics OK.
Exposition: Both the initial shock front and the initial wind behind the shock are supersonic, but the wind is slower than the shock front.
Nonetheless, the initial shock-front speed (about 2.3x103 m s–1) is still much slower than the speed of light (3x108 m s–1). Hence, we will see the lightning before we hear the thunder (except if lightning strikes you).
Sample Application (§)
Background air is calm, with temperature 300 K and pressure 100 kPa. If lightning heats the air to 30,000 K within a vertical lightning channel of radius 1.5 cm, then find and plot the evolution of average temperature inside the shock circle (relative to background temperature), average relative pressure, Mach of the shock front, and shock radius. (Namely, produce the data that was plotted in Fig. 15.27.)
Find the Answer
Given: Pb = 100 kPa, Tb = 300 K, Mb = 0 m s–1. Ta = 30,000 K initially
Find: Ta/Tb = ? , Pa/Pb = ? , Ma = ? , r = ? m and how they vary with time.
This is easily done with a spreadsheet. Because conditions vary extremely rapidly initially, and vary slower later, I will not use a constant time step for the iterations. Instead, I will use a constant ratio of
\(\ \begin{align} r_{n e w} / r_{o l d}=1.05\tag{a}\end{align}\)
Namely, I will redo the calculation for every 5% increase in shock radius. Thus,
\(\ \begin{align} t_{\text {new}}=t_{\text {old}}+\left(r_{\text {new}}-r_{\text {old}}\right) / C_{\text {old}}\tag{b}\end{align}\)
Procedure: First, enter the given background air values in cells on the spreadsheet, and compute the speed of sound in the background air.
Next, create a table in the spreadsheet that holds the following columns: r, t, Ta, Pa/Pb, Ma, C, and Te.
In the first row, start with rold = 0.015 m at told = 0, and initialize with Ta = 30,000 K. Then compute the ratio Ta/Tb, and use that ratio in eq. (15.30) to find Pa/ Pb. Use this pressure ratio to find Ma (using eq. 15.21) and C (using eq. 15.24 and knowing background sound speed). Finally, the last column in the first row is Te found using eq. (15.27).
The second row is similar to the first, except estimate the new r using eq. (a), and the new t using eq. (b). The new Ta can be found using eq. (15.28). The other columns can then be filled down into this second row. Finally, the whole second row can be filled down to as many rows as you want (be careful: do not complete the table by filling down from the first row). Some results from that spreadsheet are shown in the table in the next column.
Fig. 15.27 shows a plot of these results.
Check: Units OK. Physics OK. Some decimal places have been dropped to fit in the table on this page.
Exposition: To check for accuracy, I repeated these calculations using smaller steps (1% increase in shock radius), and found essentially the same answer.
The equations in this section for shock-front propagation are not exact. My assumption of constant density, while correct when averaged over large scales, is probably not correct at the very small scale at the shock front. Thus, my equations are an oversimplification.
| r (m) | t (s) | Ta (K) | Pa / Pb | Ma | C (m s–1) | Te (K) |
|---|---|---|---|---|---|---|
| 0.0150 | 0 | 30000 | 100.0 | 9.27 | 3210 | 5291 |
| 0.0158 | 2.34E-07 | 27703 | 92.3 | 8.90 | 3085 | 4908 |
| 0.0165 | 4.89E-07 | 25584 | 85.3 | 8.56 | 2965 | 4555 |
| 0.0174 | 7.68E-07 | 23629 | 78.8 | 8.23 | 2849 | 4229 |
| 0.0182 | 1.07E-06 | 21825 | 72.7 | 7.91 | 2739 | 3928 |
| 0.0191 | 1.41E-06 | 20161 | 67.2 | 7.60 | 2632 | 3651 |
| 0.0201 | 1.77E-06 | 18626 | 62.1 | 7.30 | 2530 | 3395 |
| 0.0211 | 2.17E-06 | 17210 | 57.4 | 7.02 | 2433 | 3159 |
| 0.0222 | 2.60E-06 | 15904 | 53.0 | 6.75 | 2339 | 2941 |
| 0.0233 | 3.07E-06 | 14699 | 49.0 | 6.49 | 2249 | 2740 |
| 0.0244 | 3.59E-06 | 13587 | 45.3 | 6.24 | 2162 | 2555 |
| 0.0257 | 4.16E-06 | 12561 | 41.9 | 6.00 | 2079 | 2384 |
| 0.0269 | 4.77E-06 | 11615 | 38.7 | 5.77 | 2000 | 2226 |
| 0.0283 | 5.45E-06 | 10742 | 35.8 | 5.55 | 1924 | 2081 |
| 0.0297 | 6.18E-06 | 9937 | 33.1 | 5.34 | 1850 | 1946 |
| 0.0312 | 6.98E-06 | 9194 | 30.6 | 5.14 | 1780 | 1822 |
| • • • | ||||||
| 0.0958 | 6.73E-05 | 1729 | 5.8 | 2.25 | 781 | 572 |
| 0.1006 | 7.35E-05 | 1621 | 5.4 | 2.19 | 757 | 553 |
| 0.1056 | 8.01E-05 | 1522 | 5.1 | 2.12 | 734 | 536 |
| 0.1109 | 8.73E-05 | 1430 | 4.8 | 2.06 | 712 | 520 |
| 0.1164 | 9.51E-05 | 1346 | 4.5 | 2.00 | 692 | 506 |
| 0.1222 | 1.03E-04 | 1268 | 4.2 | 1.94 | 672 | 492 |
| • • • | ||||||
| 3.5424 | 0.0094 | 307 | 1.02 | 1.01 | 350 | 302 |
| 3.7195 | 0.0099 | 306 | 1.02 | 1.01 | 350 | 302 |
| 3.9055 | 0.0105 | 306 | 1.02 | 1.01 | 349 | 302 |
| 4.1007 | 0.0110 | 306 | 1.02 | 1.01 | 349 | 302 |
| 4.3058 | 0.0116 | 305 | 1.02 | 1.01 | 349 | 301 |
| 4.5210 | 0.0122 | 305 | 1.02 | 1.01 | 349 | 301 |
| • • • | ||||||
| 35.091 | 0.100 | 300 | 1.00 | 1.00 | 347 | 300 |
| 36.845 | 0.105 | 300 | 1.00 | 1.00 | 347 | 300 |
| 38.687 | 0.111 | 300 | 1.00 | 1.00 | 347 | 300 |
| • • • |
15.3.6.2. Sound
By about 0.1 s after the lightning stroke, the shock wave has radius 35 m, and has almost completely slowed into a sound wave. Because this happens so quickly, and so close to the lightning channel, ignore the initial shock aspects of thunder in this subsection, and for simplicity assume that the sound waves are coming directly from the lightning channel.
The speed of sound relative to the air depends on air temperature T — sound travels faster in warmer air. But if the air also moves at wind speed M, then the total speed of sound s relative to the ground is
\(\ \begin{align} s=s_{o} \cdot\left(\frac{T}{T_{o}}\right)^{1 / 2}+M \cdot \cos (\phi)\tag{15.32}\end{align}\)
where so = 343.15 m s–1 is a reference sound speed at To = 293 K (i.e., at 20°C), and ϕ is the angle between the direction of the sound and the direction of the wind. Namely, a head-wind causes slower propagation of sound waves.
Because light travels much fasterthan sound, you can estimate the range to a lightning stroke by timing the interval ∆t between when you see lightning and hear thunder. Because sound travels roughly 1/3 km/s, divide the time interval in seconds by 3 to estimate the range in km. For range in statute miles, divide the time interval by 5 instead. These approximations are crude but useful.
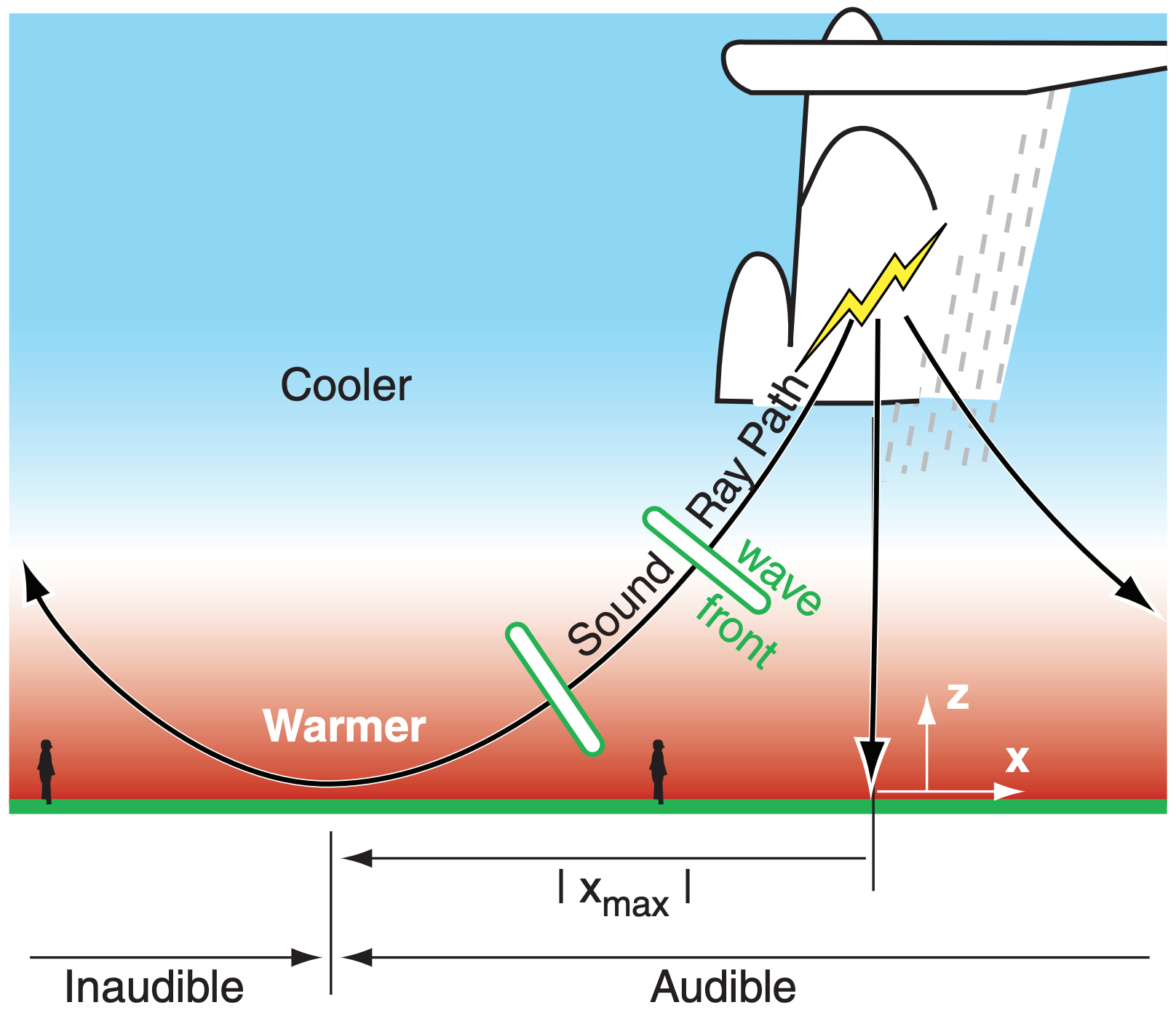
Because sound wave speed depends on temperature, the portion of a wave front in warmer air will move faster than the portion in cooler air. This causes the wave front to change its direction of advance. Thus, its propagation path (called a ray path) will bend (refract).
Consider horizontal layers of the atmosphere having different temperatures T1 and T2. If a sound wave is moving through layer one at elevation angle α1, then after passing into layer two the new ray elevation angle will be α2.
To quantify this effect, define an index of refraction for sound in calm air as:
\(\ \begin{align} n=\sqrt{T_{o} / T}\tag{15.33}\end{align}\)
where the reference temperature is To = 293 K. Snell’s law states that
\(\ \begin{align} n \cdot \cos (\alpha)= constant\tag{15.34}\end{align}\)
When applied to a sound ray moving from one layer to another, Snell’s law can be rewritten as:
\(\ \begin{align} \cos \left(\alpha_{2}\right)=\sqrt{T_{2} / T_{1}} \cdot \cos \left(\alpha_{1}\right)\tag{15.35}\end{align}\)
See the Atmospheric Optics chapter for more info.
Sample Application
You see a thunderstorm approaching from the southwest. It is warm out (T = 35°C). Facing toward the storm, you see a lightning flash and hear the thunder 12 s later, and you feel a 10 m s–1 wind on your back. What is the distance to the lightning stroke?
Find the Answer
Given: With the wind at your back, this means that the wind blowing opposite to the direction that sound must travel to reach you; hence, ϕ = 180°.
Also, ∆t = 12 s, T = 35°C = 308 K, M = 10 m s–1.
Find: ∆x = ? km
Light speed is so fast that it is effectively instantaneous. So the time interval between “flash” and “bang” depends on sound speed:
Use eq. (15.32):
s = (343.15 m s–1)·[308K/293K]1/2 + (10 m s–1)·cos(180°) = 351.8 – 10.0 = 341.8 m s–1
But speed is distance per time (s = ∆x/∆t). Rearrange:
∆x = s·∆t = (341.8 m s–1)·(12 s) = 4.102 km
Check: Physics and units OK.
Exposition: Typical wind speeds are much smaller than the speed of sound; hence, the distance calculation is only slightly affected by wind speed.
The approximate method of dividing the time interval by 3 is sometimes called the 3 second rule. This rule is simple enough to do in your head while watching the storm, and would have allowed you to estimate ∆x ≈ (12 s) / (3 s km–1) = 4 km. Close enough.
If the time interval is 30 s or less, this means the storm is 10 km or closer to you, so you should immediately seek shelter. See the lighting safety INFO boxes.
The previous expressions for Snell’s law assumed a finite step change in temperature between layers that caused a sharp kink in the ray path. But if there is a gradual temperature change with distance along the ray path, then Snell’s law for calm winds says there is a gradual bending of the ray path:
\(\ \begin{align} \Delta \alpha=\frac{\gamma}{2 \cdot T} \cdot \Delta x\tag{15.36}\end{align}\)
where ∆α is a small incremental change in ray elevation angle (radians) for each small increment of horizontal distance ∆x traveled by the light. The vertical temperature variation is expressed as a lapse rate γ = –∆T/∆z, where T is the absolute temperature of background air. As a case study, we can assume γ is constant with height, for which case the ratio in eq. (15.36) is also nearly constant because T typically varies by only a small fraction of its magnitude.
You can solve eq (15.36) iteratively. Start with a known ray angle α at a known (x, z) location, and set a small fixed ∆x value for your horizontal increment. Then, solve the following equations sequentially:
\(x_{n e w}=x_{o l d}+\Delta x\)
\(\ \begin{align} \alpha_{n e w}=\alpha_{o l d}+\Delta \alpha\tag{15.37}\end{align}\)
\(\Delta z=\Delta x \cdot \tan (\alpha)\)
\(z_{n e w}=z_{o l d}+\Delta z\)
Continue solving eqs. (15.36 & 15.37) for more steps of ∆x, using the “new” values output from the previous step as the “old” values to input for the next step. Save all the xnew and znew values, because you can plot these to see the curved ray path (Fig. 15.31).
Thunderstorms usually happen on days when the sun has heated the ground, which in turn heated the bottom of the atmosphere. Thus, temperature often decreases with increasing height on thunderstorm days. Since sound waves bend toward air that is cooler, it means the thunder ray paths tend to be concave up (Fig 15.31).
This curvature can be significant enough that there is a max distance xmax beyond which you cannot hear thunder (i.e., it is inaudible):
\(\ \begin{align} x_{\max } \cong 2 \cdot \sqrt{T \cdot z / \gamma}\tag{15.38}\end{align}\)
where the sound has originated at height z, calm winds were assumed, and T is in Kelvins.
With wind, Snell’s equation for the ray path is:
\(\ \begin{align} \frac{n \cdot(\cos \alpha)\left[1-(M a \cdot n \cdot \sin \alpha)^{2}\right]-M a \cdot(n \cdot \sin \alpha)^{2}}{1+M a \cdot n \cdot(\cos \alpha)\left[1-(M a \cdot n \cdot \sin \alpha)^{2}\right]^{1 / 2}-(M a \cdot n \cdot \sin \alpha)^{2}}=\text{constant}\tag{15.39}\end{align}\)
where Ma = M/so is the Mach number of the wind.
Sample Application (§)
Suppose lightning occurs at 4 km altitude in a thunderstorm. Assume ∆T/∆z = – 8 K/km = constant. (a) How far horizontally from the lightning can you hear the thunder? (b) For the ray path that is tangent to the ground at that xmax point, plot the ray path backwards up to the lightning. T = 308 K near the ground.
Find the Answer
Given: z = 4 km, T = 308 K, γ = 8 K km–1
Find: xmax = ? km, and plot (x, z) from z = 0 to 4 km
Use eq. (15.38): xmax = 2 · [(308 K)·(4 km) / (8 K km–1)]1/2 = 24.8 km
Pick a small ∆x = 0.5 km, and use eq. (15.36):
∆α = (8K km–1)·(0.5 km) / [2· (308K)] = 0.00649 radians
Use a spreadsheet to solve eqs. (15.37) with the constant value of ∆α calculated above. We know the sound ray is tangent to the ground (α = 0 radians) at the inaudibility point. Define x = 0 km and z = 0 km at this starting point. Then iterate eqs. (15.37) up to the altitude of the lightning.
| x (km) | α (rad) | ∆z (km) | z (km) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0.5 | 0.00649 | 0.00325 | 0.00325 |
| 1.0 | 0.01299 | 0.00649 | 0.00974 |
| 1..5 | 0.01948 | 0.00974 | 0.00195 |
| 2.0 | 0.02597 | 0.01299 | 0.03247 |
| . . . | . . . | . . . | . . . |
| 24.5 | 0.31818 | 0.16469 | 4.0477 |
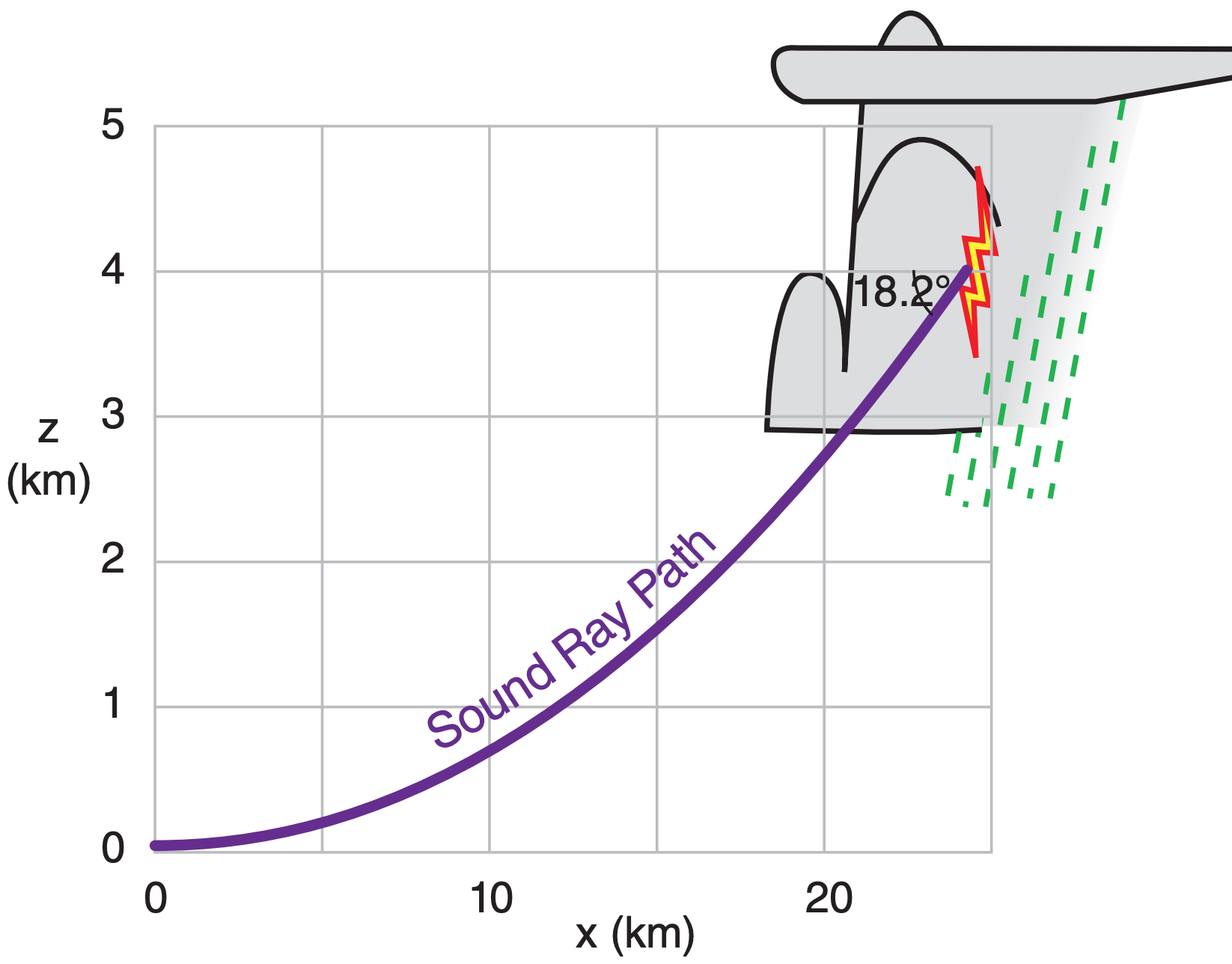
Check: Physics and units OK.
Exposition: x = 0 in the graph above is distance xmax from the lightning, where xmax was well approximated by eq. (15.38). For these weather conditions, of all the sound rays that radiated outward from the lightning origin, the one that became tangent to the ground was the one that left the storm with elevation angle 18.2° (= 0.31818 radians) downward from horizontal.


