15.1: Precipitation and Hail
- Page ID
- 9624
15.1.1. Heavy Rain
Thunderstorms are deep clouds that can create:
- large raindrops (2 - 8 mm diameter), in
- scattered showers (order of 5 to 10 km diameter rain shafts moving across the ground, resulting in brief-duration rain [1 - 20 min] over any point), of
- heavy rainfall rate (10 to over 1000 mm h–1 rainfall rates).
The Precipitation Processes chapter lists worldrecord rainfall rates, some of which were caused by thunderstorms. Compare this to nimbostratus clouds, that create smaller-size drizzle drops (0.2 - 0.5 mm) and small rain drops (0.5 - 2 mm diameter) in widespread regions (namely, regions hundreds by thousands of kilometers in size, ahead of warm and occluded fronts) of light to moderate rainfall rate that can last for many hours over any point on the ground.
Why do thunderstorms have large-size drops? Thunderstorms are so tall that their tops are in very cold air in the upper troposphere, allowing coldcloud microphysics even in mid summer. Once a spectrum of different hydrometeor sizes exists, the heavier ice particles fall faster than the smaller ones and collide with them. If the heavier ice particles are falling through regions of supercooled liquid cloud droplets, they can grow by riming (as the liquid water instantly freezes on contact to the outside of ice crystals) to form dense, conical-shaped snow pellets called graupel (< 5 mm diameter). Alternately, if smaller ice crystals fall below the 0°C level, their outer surface partially melts, causing them to stick to other partially-melted ice crystals and grow into miniature fluffy snowballs by a process called aggregation to sizes as large as 1 cm in diameter.
The snow aggregates and graupel can reach the ground still frozen or partially frozen, even in summer. This occurs if they are protected within the cool, saturated downdraft of air descending from thunderstorms (downbursts will be discussed later). At other times, these large ice particles falling through the warmer boundary layer will melt completely into large raindrops just before reaching the ground. These rain drops can make a big splat on your car windshield or in puddles on the ground.
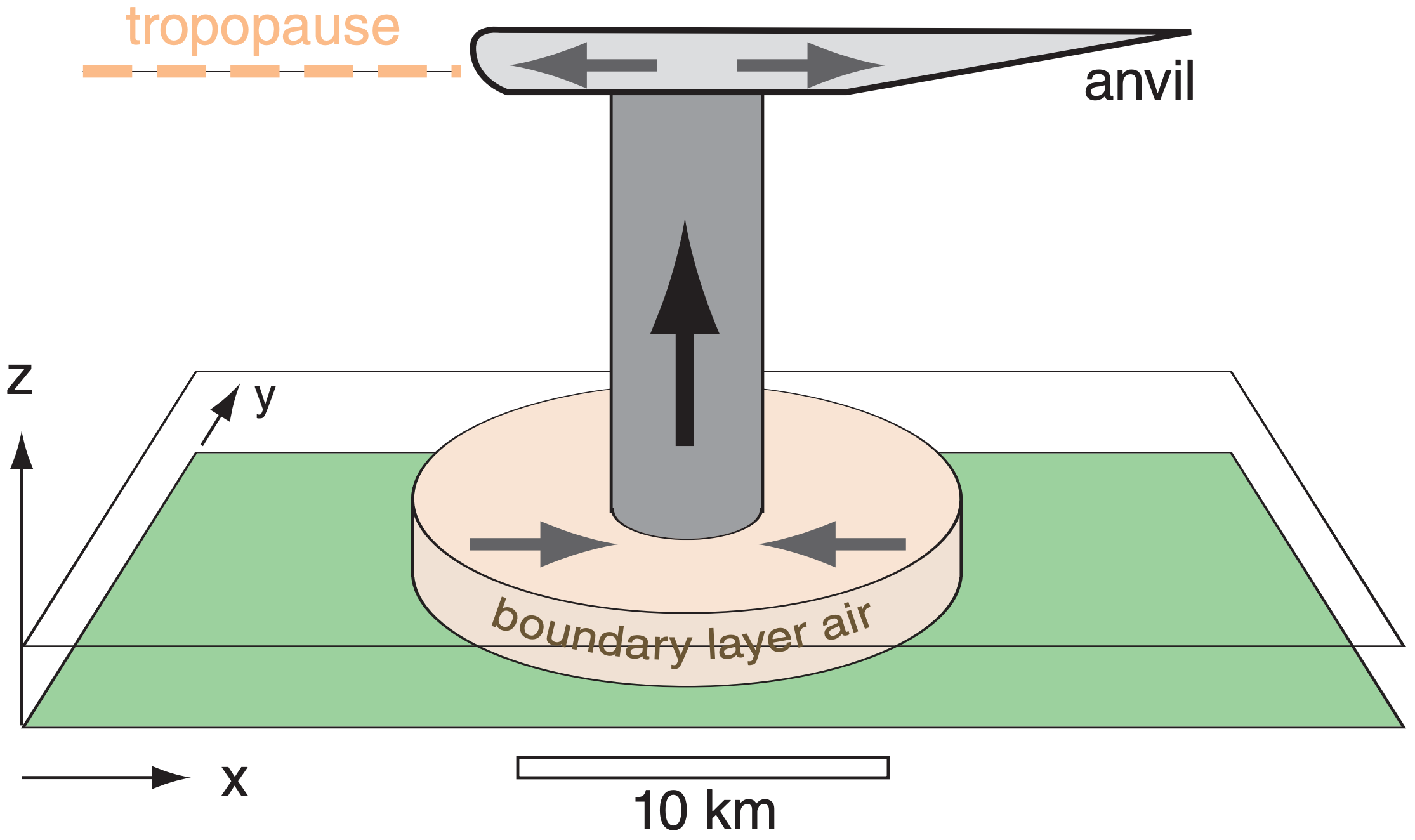
Why do thunderstorms have scattered showers? Often large-size, cloud-free, rain-free subsidence regions form around and adjacent to thunderstorms due to air-mass continuity. Namely, more air mass is pumped into the upper troposphere by thunderstorm updrafts than can be removed by in-storm precipitation-laden downdrafts. Much of the remaining excess air descends more gently outside the storm. This subsidence (Fig. 15.1) tends to suppress other incipient thunderstorms, resulting in cumulonimbus clouds that are either isolated (surrounded by relatively cloud-free air), or are in a thunderstorm line with subsidence ahead and behind the line.
Why do thunderstorms often have heavy rain?
- First, the upper portions of the cumulonimbus cloud are so high that the rising air parcels become so cold (due to the moist-adiabatic cooling rate) that virtually all of the water vapor carried by the air is forced to condense, deposit, or freeze out.
- Second, the vertical stacking of the deep cloud allows precipitation forming in the top of the storm to grow by collision and coalescence or accretion as it falls through the middle and lower parts of the cloud, as already mentioned, thus sweeping out a lot of water in a short time.
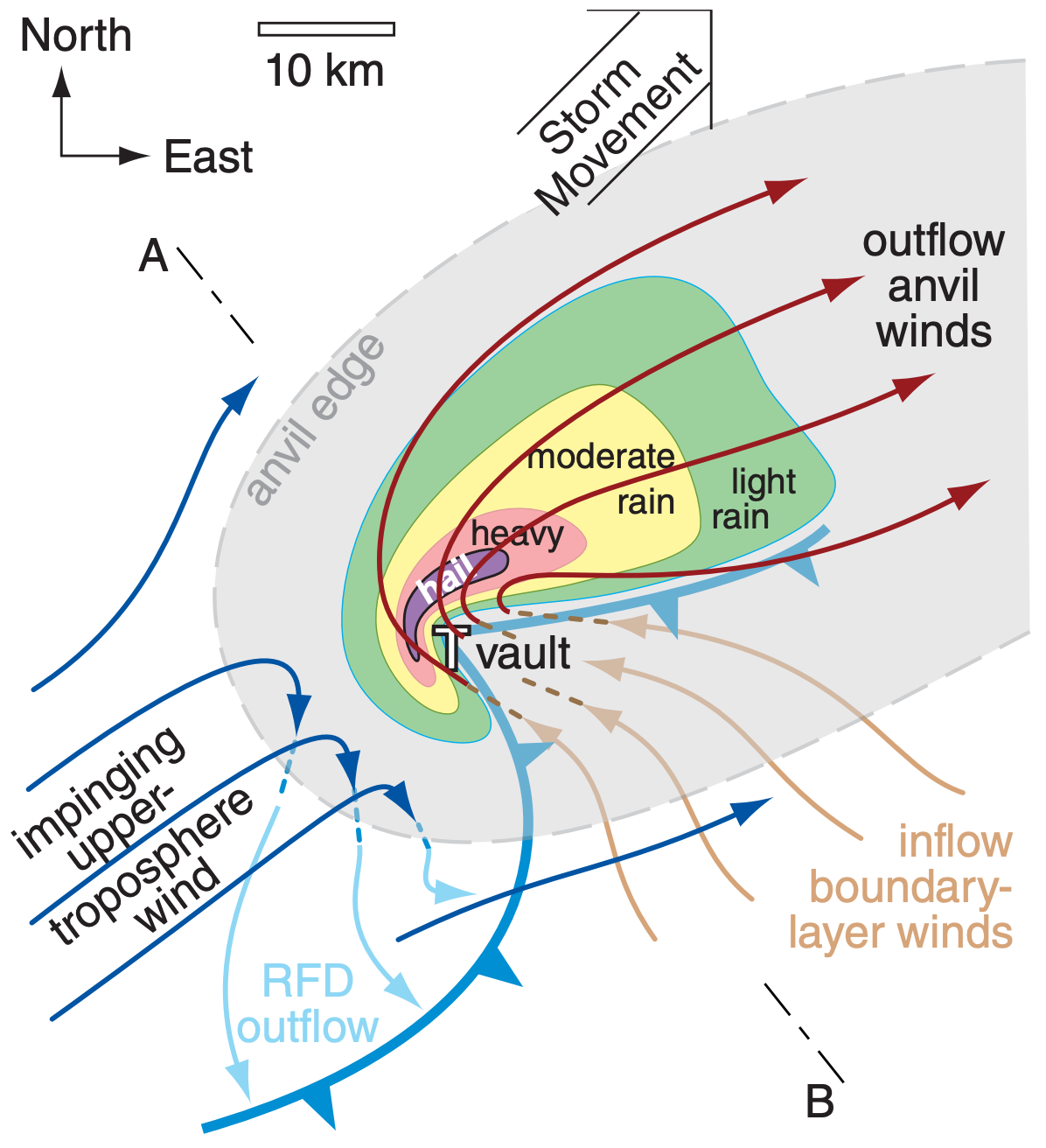
- Third, long-lasting storms such as supercells or orographic storms can have continual inflow of humid boundary-layer air to add moisture as fast as it rains out, thereby allowing the heavy rainfall to persist. As was discussed in the previous chapter, the heaviest precipitation often falls closest to the main updraft in supercells (see Fig. 15.5).
Rainbows are a by-product of having large numbers of large-diameter drops in a localized region surrounded by clear air (Fig. 15.1). Because thunderstorms are more likely to form in late afternoon and early evening when the sun angle is relatively low in the western sky, the sunlight can shine under cloud base and reach the falling raindrops. In North America, where thunderstorms generally move from the southwest toward the northeast, this means that rainbows are generally visible just after the thundershowers have passed, so you can find the rainbow looking toward the east (i.e., look toward your shadow). Rainbow optics are explained in more detail in the last chapter.
Any rain that reached the ground is from water vapor that condensed and did not re-evaporate. Thus, rainfall rate (RR) can be a surrogate measure of the rate of latent heat release:
\(\ \begin{align} H_{R R}=\rho_{L} \cdot L_{v} \cdot R R\tag{15.1}\end{align}\)
where HRR = rate of energy release in the storm over unit area of the Earth’s surface (J·s–1·m–2), ρL is the density of pure liquid water, Lv is the latent heat of vaporization (assuming for simplicity that all of the precipitation falls out in liquid form), and RR = rainfall rate. Ignoring variations in the values of water density and latent heat of vaporization, this equation reduces to:
\(\ \begin{align} H_{R R}=a \cdot R R\tag{15.2}\end{align}\)
where a = 694 (J·s–1·m–2) / (mm·h–1) , for rainfall rates in mm h–1.
The corresponding warming rate averaged over the tropospheric depth (assuming the thunderstorm fills the troposphere) was shown in the Heat chapter to be:
\(\ \begin{align} \Delta T / \Delta \mathrm{t}=b \cdot R R\tag{15.3}\end{align}\)
where b = 0.33 K (mm of rain)–1.
From the Water Vapor chapter recall that precipitable water, dw, is the depth of water in a rain gauge if all of the moisture in a column of air were to precipitate out. As an extension of this concept, suppose that pre-storm boundary-layer air of mixing ratio 20 g kg–1 was drawn up into a column filling the troposphere by the action of convective updrafts (Fig. 15.2). If cloud base was at a pressure altitude of 90 kPa and cloud top was at 30 kPa, and if half of the water in the cloudy domain were to condense and precipitate out, then eq. (4.33) says that the depth of water in a rain gauge is expected to be dw = 61 mm.
The ratio of amount of rain falling out of a thunderstorm to the inflow of water vapor is called precipitation efficiency, and ranges from 5 to 25% for storms in an environment with strong wind shear to 80 to 100% in weakly-sheared environments. The average efficiency of thunderstorms is roughly 50%. Processes that account for the non-precipitating water include anvil outflow of ice crystals that evaporate, evaporation of hydrometeors with entrained air from outside the storm, and evaporation of some of the precipitation before reaching the ground (i.e., virga).
Extreme precipitation producing rainfall rates over 100 mm h–1 are unofficially called cloudbursts. A few cloudbursts or rain gushes have been observed with rainfall rates of 1000 mm h–1, but they usually last for only a few minutes. The greater-intensity rainfall events occur less frequently, and have return periods (average time between occurrence) of order hundreds of years (see the Rainfall Rates subsection in the Precipitation chapter).
For example, a stationary orographic thunderstorm over the eastern Rocky Mountains in Colorado produced an average rainfall rate of 76 mm h–1 for 4 hours during 31 July 1976 over an area of about 11 x 11 km. A total of about 305 mm of rain fell into the catchment of the Big Thompson River, producing a flash flood that killed 139 people in the Big Thompson Canyon. This amount of rain is equivalent to a tropospheric warming rate of 25°C h–1, causing a total latent heat release of about 9.1x1016 J. This thunderstorm energy (based only on latent heat release) was equivalent to the energy from 23 one-megaton nuclear bomb explosions (given about 4x1015 J of heat per one-megaton nuclear bomb).
Sample Application
A thunderstorm near Holt, Missouri, dropped 305 mm of rain during 0.7 hour. How much net latent heat energy was released into the atmosphere over each square meter of Earth’s surface, and how much did it warm the air in the troposphere?
Find the Answer
Given: RR = 305 mm / 0.7 h = 436 mm h–1.
Duration ∆t = 0.7 h.
Find: HRR ·∆t = ? (J·m–2) ; ∆T = ? (°C)
First, multiply HRR in eq. (15.2) by ∆t:
HRR·∆t = [694 (J·s–1·m–2)/(mm·h–1)]·[436 mm h–1]·[0.7 h]· [3600s/h] = 762.5 MJ·m–2
Next, use eq. (15.3): ∆T = b·RR·∆t = (0.33 K mm–1)·(305 mm) = 101 °C
Check: Units OK, but values seem too large???
Exposition: After the thunderstorm has finished raining itself out and dissipating, why don’t we observe air that is 101°C warmer where the storm used to be? One reason is that in order to get 305 mm of rain out of the storm, there had to be a continual inflow of humid air bringing in moisture. This same air then carries away the heat as the air is exhausted out of the anvil of the storm.
Thus, the warming is spread over a much larger volume of air than just the air column containing the thunderstorm. Using the factor of 5 as estimated by the needed moisture supply, we get a much more reasonable estimate of (101°C)/5 ≈ 20°C of warming. This is still a bit too large, because we have neglected the mixing of the updraft air with additional environmental air as part of the cloud dynamics, and have neglected heat losses by radiation to space. Also, the Holt storm, like the Big Thompson Canyon storm, was an extreme event — many thunderstorms are smaller or shorter lived.
The net result of the latent heating is that the upper troposphere (anvil level) has warmed because of the storm, while the lower troposphere has cooled as a result of the rain-induced cold-air downburst. Namely, the thunderstorm did its job of removing static instability from the atmosphere, and leaving the atmosphere in a more stable state. This is a third reason why the first thunderstorms reduce the likelihood of subsequent storms.
In summary, the three reasons why a thunderstorm suppresses neighboring storms are: (1) the surrounding environment becomes stabilized (smaller CAPE, larger CIN), (2) sources of nearby boundary-layer fuel are exhausted, and (3) subsidence around the storm suppresses other incipient storm updrafts. But don’t forget about other thunderstorm processes such as gust fronts that tend to trigger new storms. Thus, competing processes work in thunderstorms, making them difficult to forecast.
This amount of rain was possible for two reasons: (1) the continual inflow of humid air from the boundary layer into a well-organized (long lasting) orographic thunderstorm (Fig 14.11), and (2) the weakly sheared environment allowed a precipitation efficiency of about 85%. Comparing 305 mm observed with 61 mm expected from a single troposphere-tall column of humid air, we conclude that the equivalent of about 5 troposphere-thick columns of thunderstorm air were consumed by the storm.
Since the thunderstorm is about 6 times as tall as the boundary layer is thick (in pressure coordinates, Fig. 15.2), conservation of air mass suggests that the Big Thompson Canyon storm drew boundary-layer air from an area about 5·6 = 30 times the cross-sectional area of the storm updraft (or 12 times the updraft radius). Namely, a thunderstorm updraft core of 5 km radius would ingest the fuel supply of boundary-layer air from within a radius of 60 km. This is another reason why subsequent storms are less likely in the neighborhood of the first thunderstorm. Namely, the “fuel tank” is empty after the first thunderstorm, until the fuel supply can be re-generated locally via solar heating and evaporation of surface water, or until fresh fuel of warm humid air is blown in by the wind. (See the Sample Application on the previous page for other reasons why a first thunderstorm can suppress later ones.)
15.1.2. Hail
Hailstones are irregularly shaped balls of ice larger than 0.5 cm diameter that fall from severe thunderstorms. The event or process of hailstones falling out of the sky is called hail. The damage path on the ground due to a moving hail storm is called a hail swath.

Most hailstones are in the 0.5 to 1.5 cm diameter range, with about 25% of the stones greater than 1.5 cm. Hailstones are called giant hail (or large or severe hail) if their diameters are between 1.9 and 5 cm. Hailstones with diameters ≥ 5 cm are called significant hail or enormous hail (Fig. 15.3). Giant and enormous hail are rare. One stone of diameter 17.8 cm was found in Nebraska, USA, in June 2003. The largest recorded hailstone had diameter 20.3 cm and weighed 878.8 g — it fell in Vivian, South Dakota, USA, on 23 July 2010.
Hailstone diameters are sometimes compared to standard size balls (ping-pong ball = 4 cm; tennis ball ≈ 6.5 cm). They are also compared to nonstandard sizes of fruit, nuts, and vegetables. One such classification is the TORRO Hailstone Diameter relationship (Table 15-1).
| Table 15-1. TORRO Hailstone Size Classification. | ||
| Size Code | Max. Diameter (cm) | Description |
| 0 | 0.5 - 0.9 | Pea |
| 1 | 1.0 - 1.5 | Mothball |
| 2 | 1.6 - 2.0 | Marble, grape |
| 3 | 2.1 - 3.0 | Walnut |
| 4 | 3.1 - 4.0 | Pigeon egg to golf ball |
| 5 | 4.1 - 5.0 | Pullet egg |
| 6 | 5.1 - 6.0 | Hen egg |
| 7 | 6.1 - 7.5 | Tennis ball to cricket ball |
| 8 | 7.6 - 9.0 | Large orange to soft ball |
| 9 | 9.1 - 10.0 | Grapefruit |
| 10 | > 10.0 | Melon |
15.1.2.1. Hail Damage
Large diameter hailstones can cause severe damage to crops, tree foliage, cars, aircraft, and sometimes buildings (roofs and windows). Damage is often greater if strong winds cause the hailstones to move horizontally as they fall. Most humans are smart enough not to be outside during a hail storm, so deaths due to hail in North America are rare, but animals can be killed. Indoors is the safest place for people in a hail storm, although inside a metal-roofed vehicle is also relatively safe. Stay away from windows, which can break.
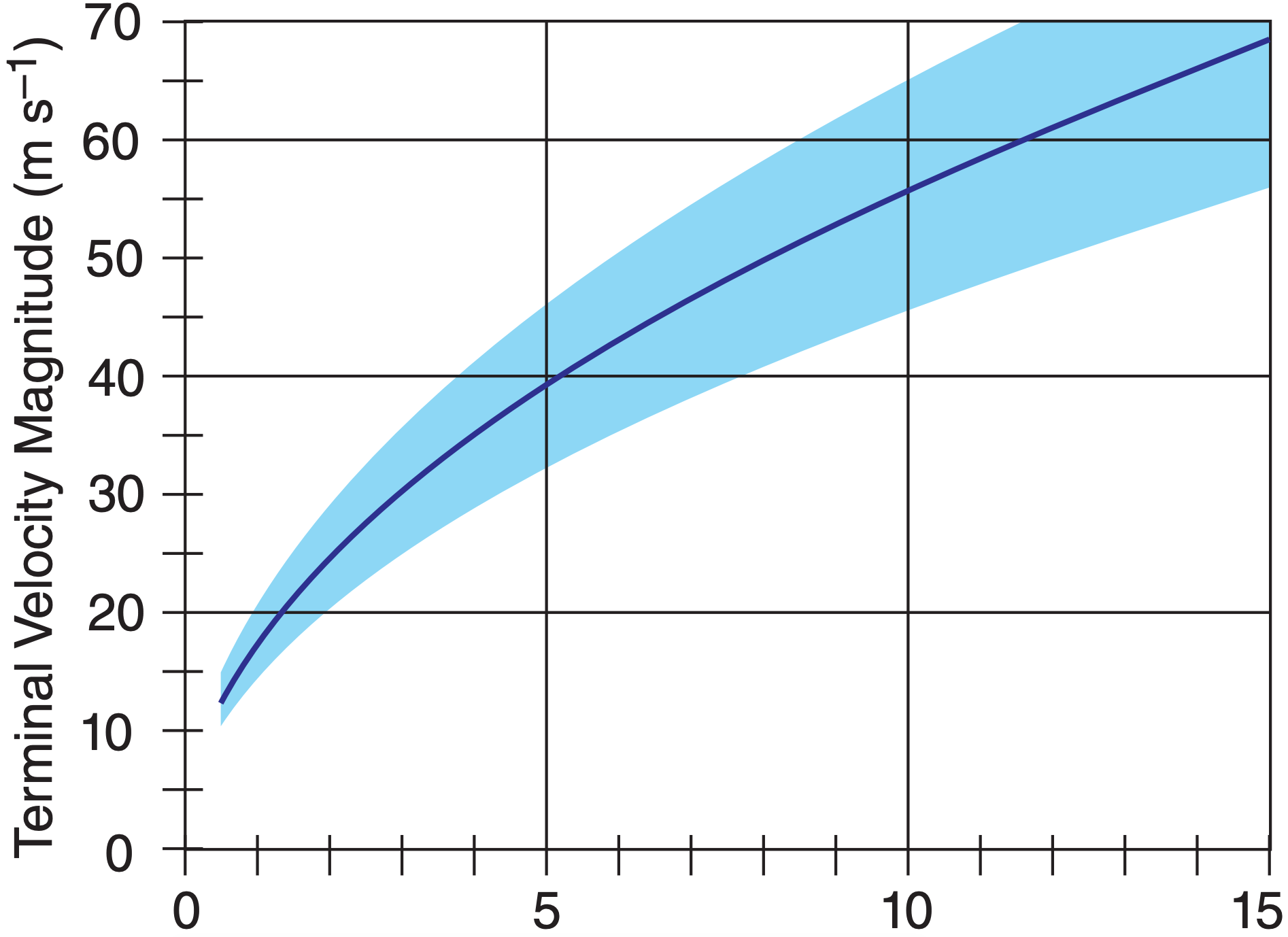
The terminal fall velocity of hail increases with hailstone size, and can reach magnitudes greater than 50 m s–1 for large hailstones. An equation for hailstone terminal velocity was given in the Precipitation chapter, and a graph of it is shown here in Fig. 15.4. Hailstones have different shapes (smooth and round vs. irregular shaped with protuberances) and densities (average ρice is 900 kg m–3, but this varies depending on the amount of air bubbles). This causes a range of air drags (0.4 to 0.8, with average 0.55) and a corresponding range of terminal fall speeds. Hailstones that form in the updraft vault region of a supercell thunderstorm are so heavy that most fall immediately adjacent to the vault (Fig. 15.5).
15.1.2.2. Hail Formation
Two stages of hail development are embryo formation, and then hailstone growth. A hail embryo is a large frozen raindrop or graupel particle (< 5 mm diameter) that is heavy enough to fall at a different speed than the surrounding smaller cloud droplets. It serves as the nucleus of hailstones. Like all normal (non-hail) precipitation, the embryo first rises in the updraft as a growing cloud droplet or ice crystal that eventually becomes large enough (via collision and accretion, as discussed in the Precipitation chapter) to begin falling back toward Earth.
While an embryo is being formed, it is still so small that it is easily carried up into the anvil and out of the thunderstorm, given typical severe thunderstorm updrafts of 10 to 50 m s–1. Most potential embryos are removed from the thunderstorm this way, and thus cannot then grow into hailstones.
The few embryos that do initiate hail growth are formed in regions where they are not ejected from the storm, such as: (1) outside of the main updraft in the flanking line of cumulus congestus clouds or in other smaller updrafts, called feeder cells; (2) in a side eddy of the main updraft; (3) in a portion of the main updraft that tilts upshear; or (4) earlier in the evolution of the thunderstorm while the main updraft is still weak. Regardless of how they are formed, it is believed that the embryos then move or fall into the main updraft of the severe thunderstorm a second time.
The hailstone grows during this second trip through the updraft. Even though the embryo is initially rising in the updraft, the smaller surrounding supercooled cloud droplets are rising faster (because their terminal fall velocity is slower), and collide with the embryo. Because of this requirement for abundant supercooled cloud droplets, hail forms at altitudes where the air temperature is between –10 and –30°C. Most growth occurs while the hailstones are floating in the updraft while drifting horizontally across the updraft in a narrow altitude range having temperatures of –15 to –20°C.
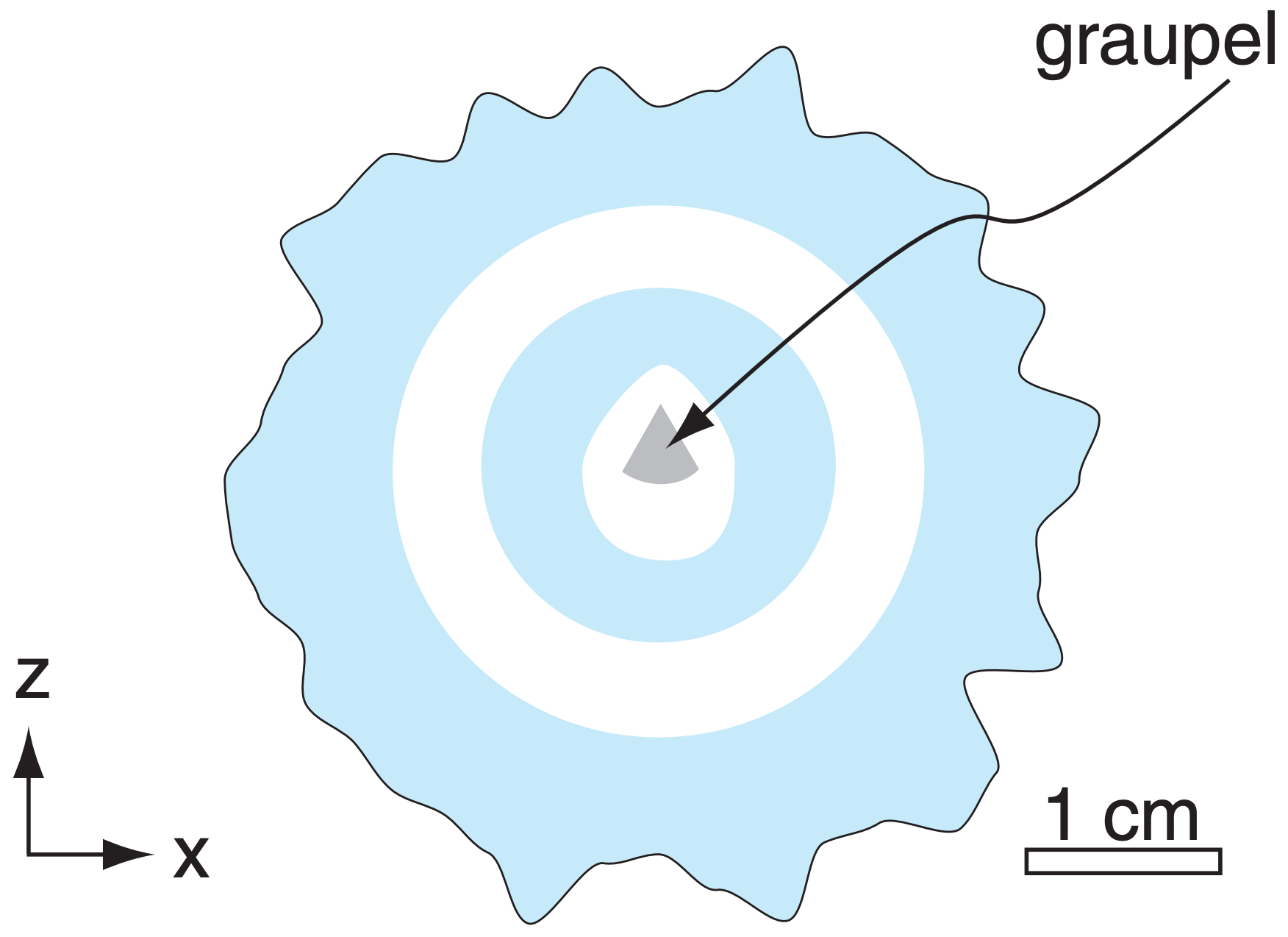
In pockets of the updraft happening to have relatively low liquid water content, the supercooled cloud droplets can freeze almost instantly when they hit the hailstone, trapping air in the interstices between the frozen droplets. This results in a porous, brittle, white layer around the hailstone. In other portions of the updraft having greater liquid water content, the water flows around the hail and freezes more slowly, resulting in a hard clear layer of ice. The result is a hailstone with 2 to 4 visible layers around the embryo (when the hailstone is sliced in half, as sketched in Fig. 15.6), although most hailstones are small and have only one layer. Giant hail can have more than 4 layers.
As the hailstone grows and becomes heavier, its terminal velocity increases and eventually surpasses the updraft velocity in the thunderstorm. At this point, it begins falling relative to the ground, still growing on the way down through the supercooled cloud droplets. After it falls into the warmer air at low altitude, it begins to melt. Almost all strong thunderstorms have some small hailstones, but most melt into large rain drops before reaching the ground. Only the larger hailstones (with more frozen mass and quicker descent through the warm air) reach the ground still frozen as hail (with diameters > 5 mm).
Sample Application
If a supercooled cloud droplet of radius 50 µm and temperature –20°C hits a hailstone, will it freeze instantly? If not, how much heat must be conducted out of the droplet (to the hailstone and the air) for the droplet to freeze?
Find the Answer
Given: r = 50 µm = 5x10–5 m, T = –20°C
Find: ∆QE = ? J , ∆QH = ? J, Is ∆QE < ∆QH ? If no, then find ∆QE – ∆QH .
Use latent heat and specific heat for liquid water, from Appendix B.
Assume a spherical droplet of mass
mliq = ρliq·Vol = ρliq·(4/3)·π·r3 = (1000 kg m–3)·(4/3)·π·(5x10–5 m)3 = 5.2x10–10 kg
Use eq. (3.3) to determine how much heat must be removed to freeze the whole droplet (∆m = mliq):
∆QE = Lf ·∆m = (3.34x105 J kg–1)·(5.2x10–10 kg) = 1.75x10–4 J .
Use eq. (3.1) to find how much can be taken up by allowing the droplet to warm from –20°C to 0°C:
∆QH = mliq·Cliq ·∆T = (5.2x10–10 kg)·[4217.6 J (kg·K)–1]·[0°C–(–20°C)] = 0.44x10–4 J .
Thus ∆QE > ∆QH , so the sensible-heat deficit associated with –20°C is not enough to compensate for the latent heat of fusion needed to freeze the drop. The droplet will NOT freeze instantly.
The amount of heat remaining to be conducted away to the air or the hailstone to allow freezing is:
∆Q = ∆QE – ∆QH = (1.75x10–4 J) – (0.44x10–4 J) = 1.31x10–4 J .
Check: Units OK. Physics OK.
Exposition: During the several minutes needed to conduct away this heat, the liquid can flow over the hailstone before freezing, and some air can escape. This creates a layer of clear ice.
15.1.2.3. Hail Forecasting
Forecasting large-hail potential later in the day is directly tied to forecasting the maximum updraft velocity in thunderstorms, because only in the stronger updrafts can the heavier hailstones be kept aloft against their terminal fall velocities (Fig. 15.4). CAPE is an important parameter in forecasting updraft strength, as was given in eqs. (14.7) and (14.8) of the Thunderstorm chapter. Furthermore, since it takes about 40 to 60 minutes to create hail (including both embryo and hail formation), large hail would be possible only from long-lived thunderstorms, such as supercells that have relatively steady organized updrafts (which can exist only in an environment with appropriate wind shear).
However, even if all these conditions are satisfied, hail is not guaranteed. So national forecast centers in North America do not issue specific hail watches, but include hail as a possibility in severe thunderstorm watches and warnings.
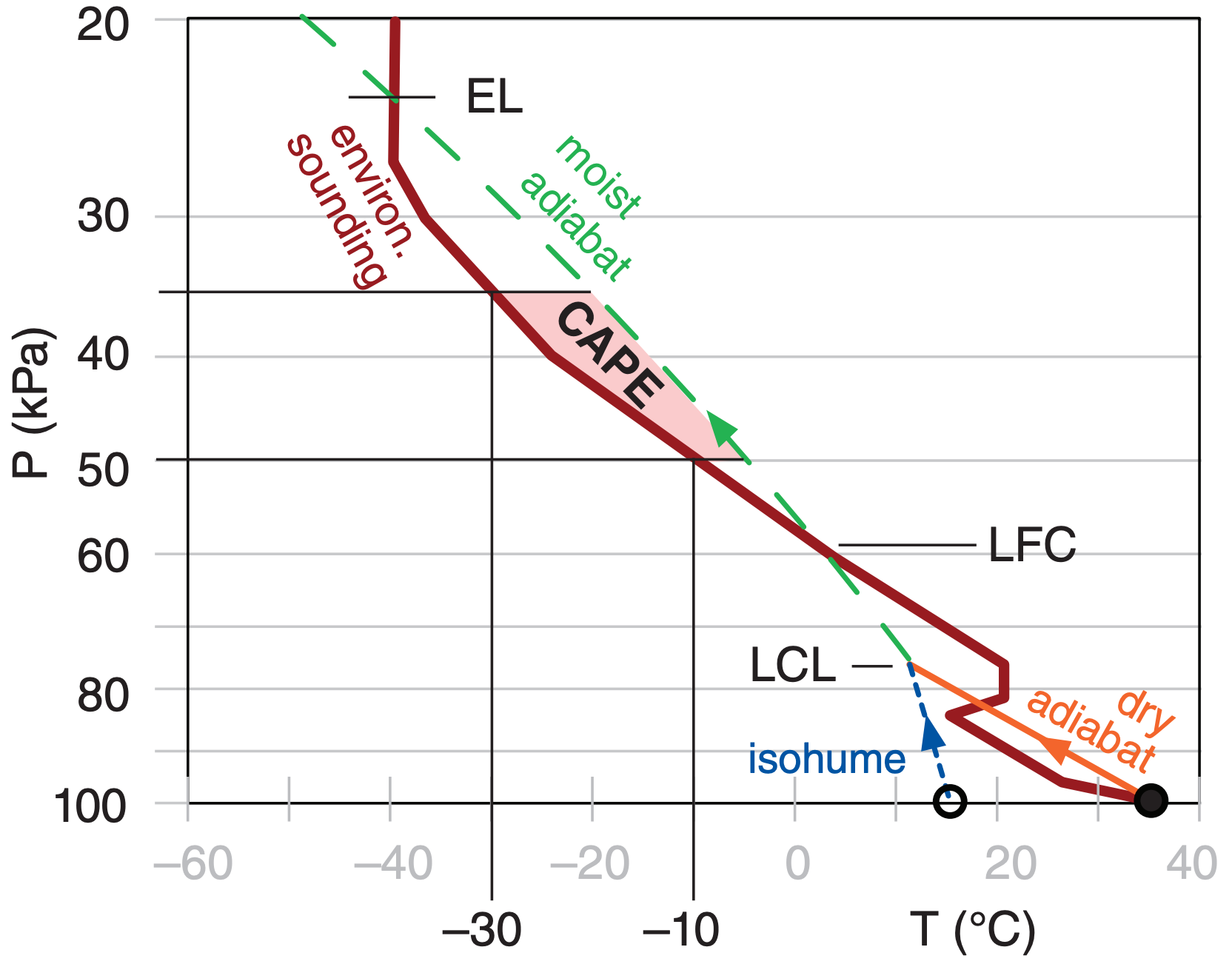
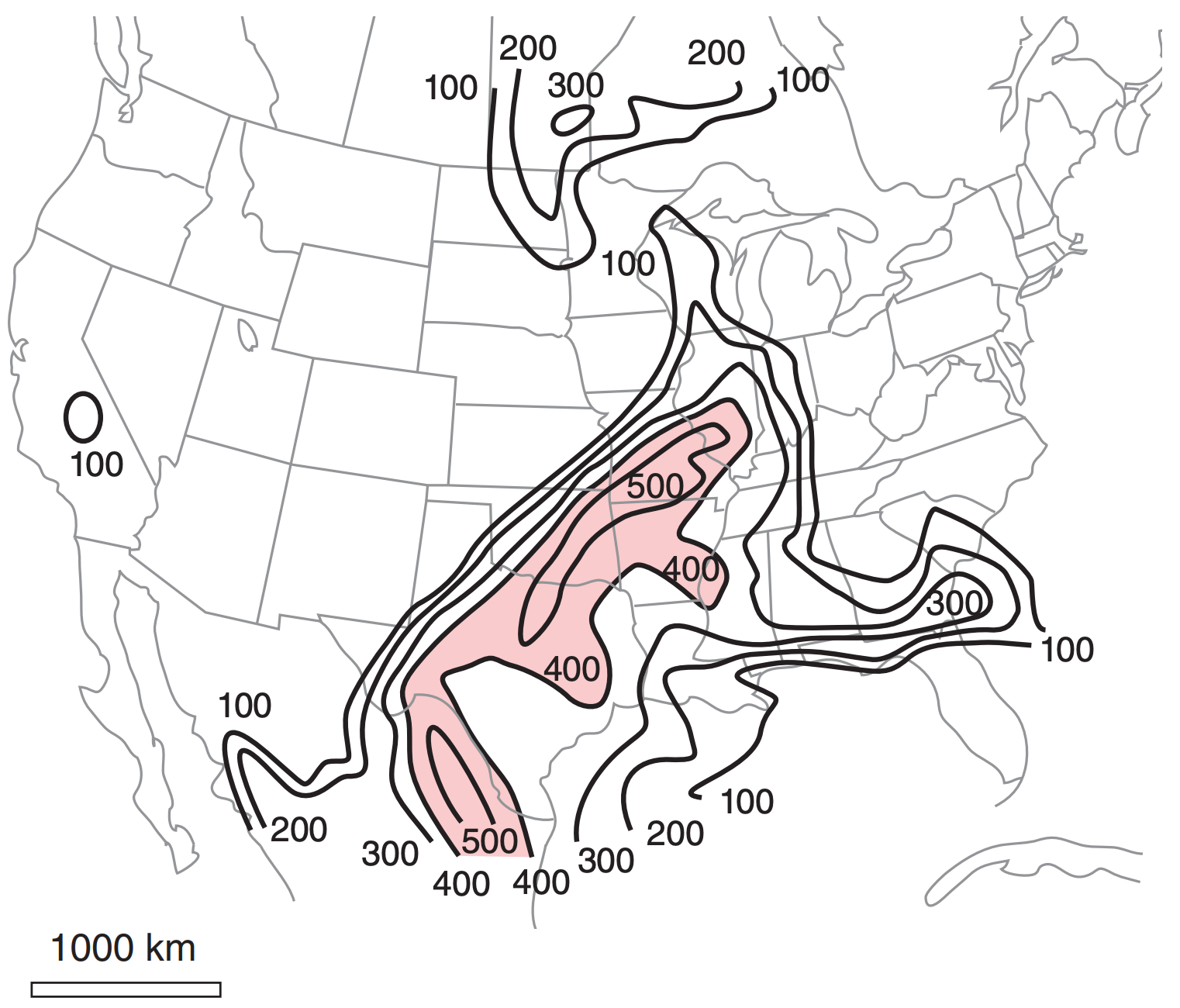
To aid in hail forecasting, meteorologists sometimes look at forecast maps of the portion of CAPE between altitudes where the environmental air temperature is –30 ≤ T ≤ –10°C, such as sketched in Fig. 15.7. Larger values (on the order of 400 J kg–1 or greater) of this portion of CAPE are associated with more rapid hail growth. Computers can easily calculate this portion of CAPE from soundings produced by numerical forecast models, such as for the case shown in Fig. 15.8. Within the shaded region of large CAPE on this figure, hail would be forecast at only those subsets of locations where thunderstorms actually form.
Weather maps of freezing-level altitude and wind shear between 0 to 6 km are also used by hail forecasters. More of the hail will reach the ground without melting if the freezing level is at a lower altitude. Environmental wind shear enables longer-duration supercell updrafts, which favor hail growth.
Research is being done to try to create a single forecast parameter that combines many of the factors favorable for hail. One example is the Significant Hail Parameter (SHIP):
\(\begin{align} S H I P &=\left\{\operatorname{MUCAPE}\left(\mathrm{J} \mathrm{kg}^{-1}\right) \cdot r_{\operatorname{MUP}}\left(\mathrm{g} \mathrm{kg}^{-1}\right)\right.\cdot \gamma_{70-50 k P a}\left(^{\circ} \mathrm{Ckm}^{-1}\right) \cdot\left[-T_{50 k P a}\left(^{\circ} \mathrm{C}\right)\right] \cdot\left.T S M_{0-6 k m}\left(\mathrm{m} \mathrm{s}^{-1}\right)\right\} / a \tag{15.4}\end{align}\)
where rMUP is the water vapor mixing ratio for the most-unstable air parcel, γ70-50kPa is the average environmental lapse rate between pressure heights 70 and 50 kPa, T50kPa is the temperature at a pressure height of 50 kPa, TSM0-6km is the total shear magnitude between the surface and 6 km altitude, and empirical parameter a = 44x106 (with dimensions equal to those shown in the numerator of the equation above, so as to leave SHIP dimensionless).
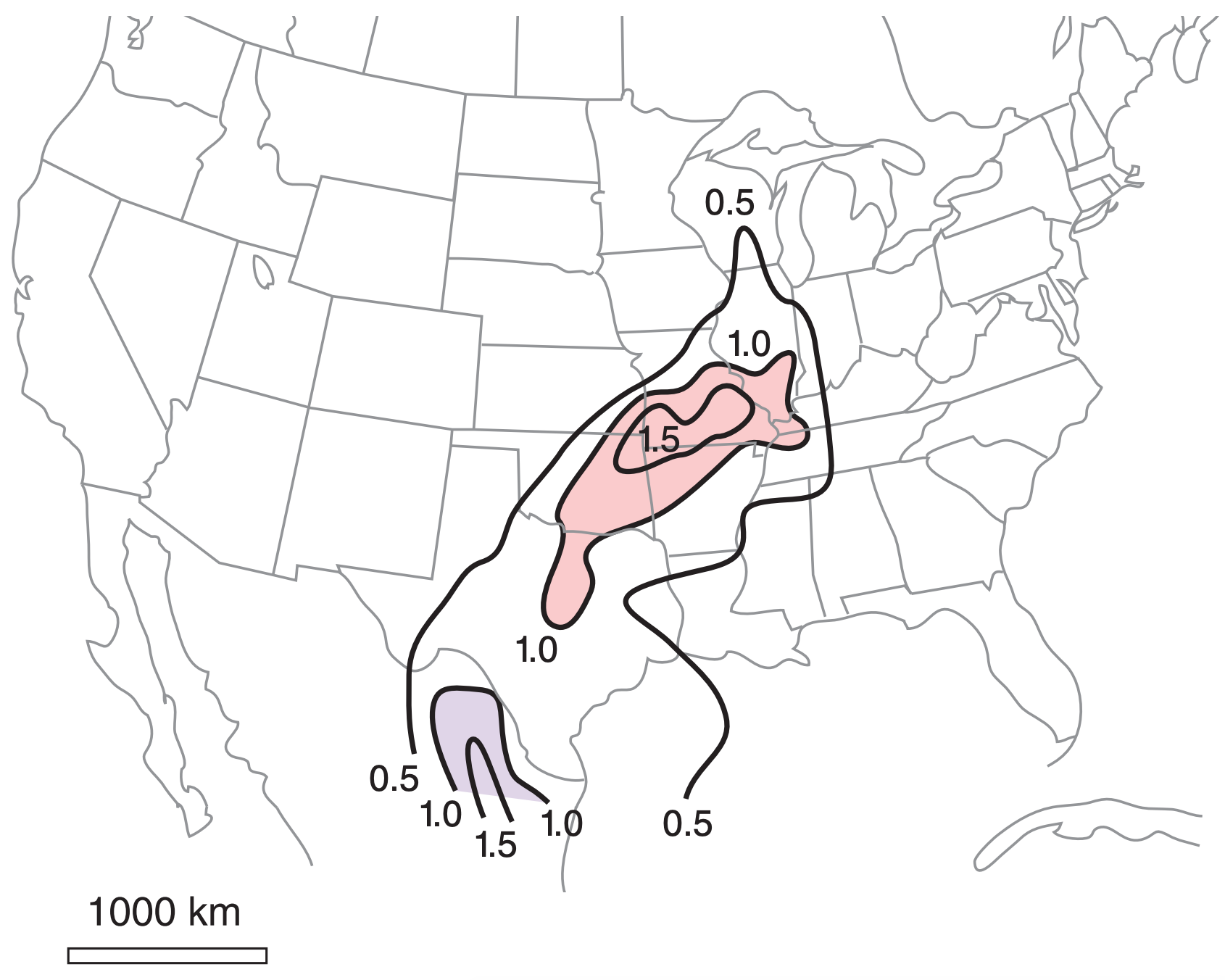
This parameter typically ranges from 0 to 4 or so. If SHIP > 1, then the prestorm environment is favorable for significant hail (i.e., hail diameters ≥ 5 cm). Significant hail is frequently observed when SHIP ≥ 1.5. Fig. 15.9 shows a weather map of SHIP for the 22 UTC 24 May 2006 case study.
Nowcasting (forecasting 1 to 30 minutes ahead) large hail is aided with weather radar:
- Large hailstones cause very large radar reflectivity (order of 60 to 70 dBZ) compared to the maximum possible from very heavy rain (up to 50 dBZ). Some radar algorithms diagnose hail when it finds reflectivities ≥ 40 dBZ at altitudes where temperatures are below freezing, with greater chance of hail for ≥ 50 dBZ at altitudes above the –20°C level.
- Doppler velocities can show if a storm is organized as a supercell, which is statistically more likely to support hail.
- Polarimetric methods (see the Satellites & Radar chapter) allow radar echoes from hail to be distinguished from echoes from rain or smaller ice particles.
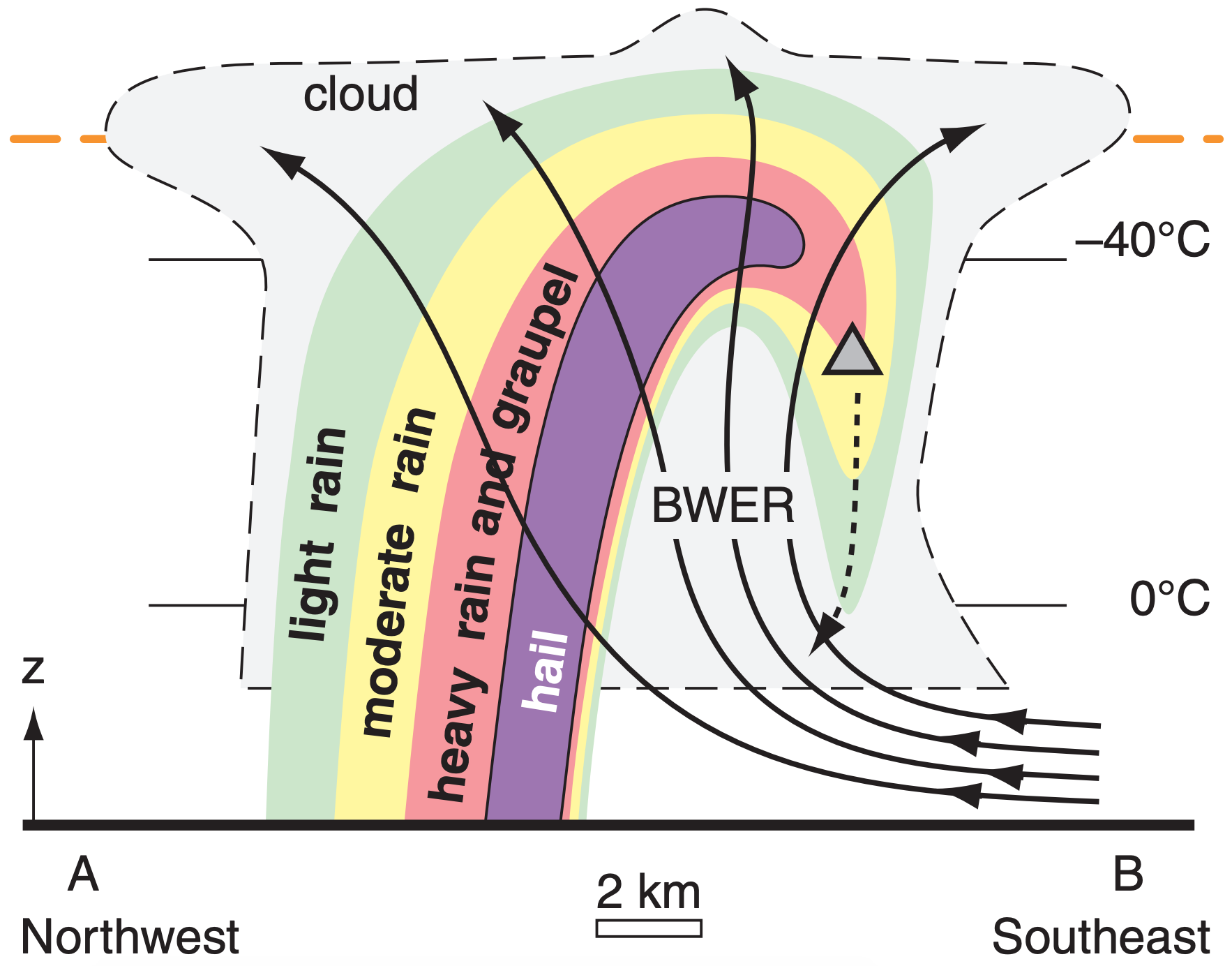
- The updrafts in some supercell thunderstorms are so strong that only small cloud droplets exist, causing weak (<25 dBZ) radar reflectivity, and resulting in a weak-echo region (WER) on the radar display. Sometimes the WER is surrounded on the top and sides by strong precipitation echoes, causing a bounded weak-echo region (BWER), also known as an echo-free vault. This enables very large hail, because embryos falling from the upshear side of the bounding precipitation can re-enter the updraft, thereby efficiently creating hail (Fig. 15.10).
Sample Application
Suppose a pre-storm environmental sounding has the following characteristics over a corn field:
MUCAPE = 3000 J kg–1,
rMUP = 14 g kg–1,
γ70-50kPa = 5 °C km–1,
T50kPa = –10°C
TSM0-6km = 45 m s–1
If a thunderstorm forms in this environment, would significant hail (with diameters ≥ 5 cm) be likely?
Find the Answer
Given: values listed above
Find: SHIP = ? .
Use eq. (15.4):
SHIP = [ (3000 J kg–1) · (14 g kg–1) · (5 °C km–1) · (10°C) · (45 m s–1) ] / (44x106) = 99.5x106 / (44x106) = 2.15
Check: Units are dimensionless. Value reasonable.
Exposition: Because SHIP is much greater than 1.0, significant (tennis ball size or larger) hail is indeed likely. This would likely totally destroy the corn crop. Because hail forecasting has so many uncertainties and often short lead times, the farmers don’t have time to take action to protect or harvest their crops. Thus, their only recourse is to purchase crop insurance.
15.1.2.4. Hail Locations
The hail that does fall often falls closest to the main updraft (Figs. 15.5 & 15.10), and the resulting hail shaft (the column of falling hailstones below cloud base) often looks white or invisible to observers on the ground. Most hail falls are relatively short lived, causing small (10 to 20 km long, 0.5 to 3 km wide) damage tracks called hailstreaks. Sometimes long-lived supercell thunderstorms can create longer hailswaths of damage 8 to 24 km wide and 160 to 320 km long. Even though large hail can be extremely damaging, the mass of water in hail at the ground is typically only 2 to 3% of the mass of rain from the same thunderstorm.
In the USA, most giant hail reaching the ground is found in the central and southern plains, centered in Oklahoma (averaging 6 to 9 giant-hail days yr–1), and extending from Texas north through Kansas and Nebraska (3 or more giant-hail days yr–1). Hail is also observed less frequently (1 to 3 giant-hail days yr–1) eastward across the Mississippi valley and into the southern and mid-Atlantic states.
Although hail is less frequent in Canada than in the USA, significant hail falls are found in Alberta between the cities of Calgary and Edmonton, particularly near the town of Red Deer. Hail is also found in central British Columbia, and in the southern prairies of Saskatchewan and Manitoba.
In the S. Hemisphere, hail falls often occur over eastern Australia. The 14 April 1999 hailstorm over Sydney caused an estimated AUS$ 2.2 billion in damage, the second largest weather-related damage total on record for Australia. Hailstorms have been observed over North and South America, Europe, Australia, Asia, and Africa.
15.1.2.5. Hail Mitigation
Attempts at hail suppression (mitigation) have generally been unsuccessful, but active hail-suppression efforts still continue in most continents to try to reduce crop damage. Five approaches have been suggested for suppressing hail, all of which involve cloud seeding (adding particles into clouds to serve as additional or specialized hydrometeor nuclei), which is difficult to do with precision:
- beneficial competition - to create larger numbers of embryos that compete for supercooled cloud water, thereby producing larger numbers of smaller hailstones (that melt before reaching the ground). The methods are cloud seeding with hygroscopic (attracts water; e.g., salt particles) cloud nuclei (to make larger rain drops that then freeze into embryos), or seeding with glaciogenic (makes ice; e.g., silver iodide particles) ice nuclei to make more graupel.
- early rainout - to cause precipitation in the cumulus congestus clouds of the flanking line, thereby reducing the amount of cloud water available before the updraft becomes strong enough to support large hail. The method is seeding with ice nuclei.
- trajectory altering - to cause the embryos to grow to greater size earlier, thereby following a lower trajectory through the updraft where the temperature or supercooled liquid water content is not optimum for large hail growth. This method attempts to increase rainfall (in drought regions) while reducing hail falls.
- dynamic effects - to consume more CAPE earlier in the life cycle of the updraft (i.e., in the cumulus congestus stage), thereby leaving less energy for the main updraft, causing it to be weaker (and supporting only smaller hail).
- glaciation of supercooled cloud water - to more quickly convert the small supercooled cloud droplets into small ice crystals that are less likely to stick to hail embryos and are more likely to be blown to the top of the storm and out via the anvil. This was the goal of most of the early attempts at hail suppression, but has lost favor as most hail suppression attempts have failed.
For many years there has been a very active cloud seeding effort near the town of Red Deer, Alberta, Canada, in the hopes of suppressing hail. These activities were funded by some of the crop-insurance companies, because their clients, the farmers, demanded that something be done.
Although the insurance companies knew that there is little solid evidence that hail suppression actually works, they funded the cloud seeding anyway as a public-relations effort. The farmers appreciated the efforts aimed at reducing their losses, and the insurance companies didn’t mind because the cloudseeding costs were ultimately borne by the farmers via increased insurance premiums.
Sample Application
During cloud seeding, how many silver iodide particles need to be introduced into a thunderstorm to double the number of ice nuclei? Assume the number density of natural ice nuclei is 10,000 per cubic meter.
Find the Answer
Given: nice nuclei/Volume = 10,000 m–3
Find: Ntotal = ? total count of introduced nuclei
To double ice nuclei, the count of introduced nuclei must equal the count of natural nuclei:
Ntotal = ( nice nuclei/Volume) · Volume
Estimate the volume of a thunderstorm above the freezing level. Assume freezing level is at 3 km altitude, and the anvil top is at 12 km. Approximate the thunderstorm by a box of bottom surface area 12 x 12 km, and height 9 km (= 12 – 3).
Volume ≈ 1300 km3 = 1.3x1012 m3
Thus:
Ntotal = ( nice nuclei/Volume) · Volume = (10,000 m–3) · (1.3x1012 m3) = 1.3x1016
Check: Units OK. Physics OK.
Exposition: Cloud seeding is often done by an aircraft. For safety reasons, the aircraft doesn’t usually fly into the violent heart of the thunderstorm. Instead, it flies under the rain-free portion of cloud base, releasing the silver iodide particles into the updraft in the hopes that the nuclei get to the right part of the storm at the right time. It is not easy to do this correctly, and even more difficult to confirm if the seeding caused the desired change. Seeding thunderstorms is an uncontrolled experiment, and one never knows how the thunderstorm would have changed without the seeding.


