13.3: Lee Cyclogenesis
- Page ID
- 9612
Recall from the General Circulation chapter that the west-to-east jet stream can meander poleward and equatorward as Rossby waves, due to barotropic and baroclinic instability. Such waves in the upper-air (jet-stream) flow can create mid-latitude cyclones at the surface, as shown in Figs. 13.6 & 13.7.
One trigger mechanism for this instability is flow over high mountain ranges. The Rossby wave triggered by such a mountain often has a trough just downwind of (i.e.., to the “lee” of) mountain ranges. East of this trough is a favored location for cyclogenesis; hence, it is known as lee cyclogenesis. Because the mountain location is fixed, the resulting Rossby-wave trough and ridge locations are stationary with respect to the mountain-range location.
Synoptic meteorology is the study and analysis of weather maps, often with the aim to forecast the weather on horizontal scales of 400 to 4000 km. Syn- optic weather maps describe an instantaneous state of the atmosphere over a wide area, as created from weather observations made nearly simultaneously.
Typical weather phenomena at these synoptic scales include cyclones (Lows), anticyclones (Highs), and airmasses. Fronts are also included in synoptics because of their length, even though frontal zones are so narrow that they can also be classified as mesoscale. See Table 10-6 and Fig. 10.24 in the Atmospheric Forces & Winds chapter for a list of different atmospheric scales.
The material in this chapter and in the previous one fall solidly in the field of synoptics. People who specialize in synoptic meteorology are called synopticians.
The word “synoptics” is from the Greek “synoptikos”, and literally means “seeing everything together”. It is the big picture.
13.3.1. Stationary Rossby Waves
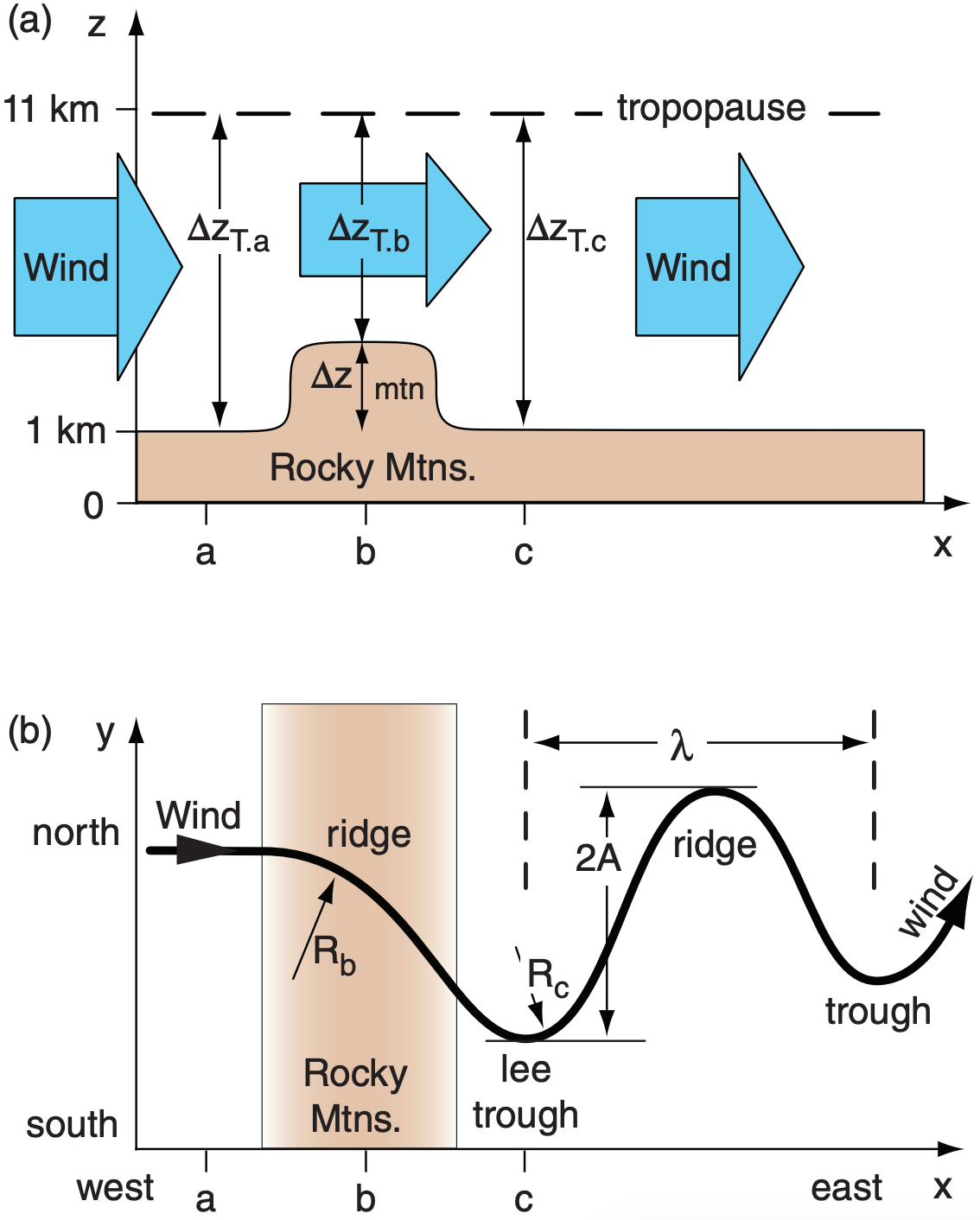
Consider a wind that causes air in the troposphere to blow over the Rocky mountains (Fig. 13.20). Convective clouds (e.g., thunderstorms) and turbulence can cause the Rossby wave amplitude to decrease further east, so the first wave after the mountain (at location c in Fig. 13.20) is the one you should focus on.
These Rossby waves have a dominant wavelength (λ) of roughly
\(\ \begin{align} \lambda \approx 2 \cdot \pi \cdot\left[\frac{M}{\beta}\right]^{1 / 2}\tag{13.1}\end{align}\)
where the mean wind speed is M. As you have seen in an earlier chapter, β is the northward gradient of the Coriolis parameter (fc):
\(\ \begin{align} \beta=\frac{\Delta f_{C}}{\Delta y}=\frac{2 \cdot \Omega}{R_{\text {earth }}} \cdot \cos \phi\tag{13.2}\end{align}\)
Factor 2·Ω = 1.458x10–4 s–1 is twice the angular rotation rate of the Earth. At North-American latitudes, β is roughly 1.5 to 2x10–11 m–1 s–1.
Knowing the mountain-range height (∆zmtn) relative to the surrounding plains, and knowing the initial depth of the troposphere (∆zT), the Rossby-wave amplitude A is:
\(\ \begin{align} A \approx \frac{f_{c}}{\beta} \cdot \frac{\Delta z_{m t n}}{\Delta z_{T}}\tag{13.3}\end{align}\)
Because β is related to fc, we can analytically find their ratio as fc/β = REarth·tan(ϕ), where the average radius (REarth) of the Earth is 6371 km. Over North America the tangent of the latitude ϕ is tan(ϕ) ≈ 1. Thus:
\(\ \begin{align} A \approx \frac{\Delta z_{m t n}}{\Delta z_{T}} \cdot R_{e a r t h}\tag{13.4}\end{align}\)
where 2A is the ∆y distance between the wave trough and crest.
In summary, the equations above show that north-south Rossby-wave amplitude depends on the height of the mountains, but does not depend on wind speed. Conversely, wind speed is important in determining Rossby wavelength, while mountain height is irrelevant.
Sample Application
What amplitude & wavelength of terrain-triggered Rossby wave would you expect for a mountain range at 48°N that is 1.2 km high? The upstream depth of the troposphere is 11 km, with upstream wind is 19 m s–1.
Find the Answer
Given: ϕ = 48°N, ∆zmtn = 1.2 km, ∆zT = 11 km, M = 19 m s–1.
Find: A = ? km , λ = ? km
Use eq. (13.4):
A = [ (1.2 km) / (11 km) ] · (6371 km) = 695 km
Next, use eq. (13.2) to find β at 48°N:
β = (2.294x10–11 m–1·s–1) · cos(48°) = 1.53x10–11 m–1·s–1
Finally, use eq. (13.1):
\(\lambda \approx 2 \cdot \pi \cdot\left[\frac{19 \mathrm{m} \cdot \mathrm{s}^{-1}}{1.53 \times 10^{-11} \mathrm{m}^{-1} \cdot \mathrm{s}^{-1}}\right]^{1 / 2}=\underline{6990} \mathrm{km}\)
Check: Physics and units are reasonable.
Exposition: Is this wave truly a planetary wave? Yes, because its wavelength (6,990 km) would fit 3.8 times around the Earth at 48°N (circumference = 2·π·REarth·cos(48°) = 26,785 km). Also, the north-south meander of the wave spans 2A = 12.5° of latitude.
13.3.2. Potential-vorticity Conservation
Use conservation of potential vorticity as a tool to understand such mountain lee-side Rossby-wave triggering (Fig. 13.20). Create a “toy model” by assuming wind speed is constant in the Rossby wave, and that there is no wind shear affecting vorticity. For this situation, the conservation of potential vorticity ζp is given by eq. (11.25) as:
\(\ \begin{align} \zeta_{p}=\frac{(M / R)+f_{c}}{\Delta z}= constant\tag{13.5}\end{align}\)
For this toy model, consider the initial winds to be blowing straight toward the Rocky Mountains from the west. These initial winds have no curvature at location “a”, thus R = ∞ and eq. (13.5) becomes:
\(\ \begin{align} \zeta_{p}=\frac{f_{c . a}}{\Delta z_{T, a}}\tag{13.6}\end{align}\)
where ∆zT.a is the average depth of troposphere at point “a”. Because potential vorticity is conserved, we can use this fixed value of ζp to see how the Rossby wave is generated.
Let ∆zmtn be the relative mountain height above the surrounding land (Fig. 13.20a). As the air blows over the mountain range, the troposphere becomes thinner as it is squeezed between mountain top and the tropopause at location “b”: ∆zT.b = ∆zT.a – ∆zmtn. But the latitude of the air hasn’t changed much yet, so fc.b ≈ fc.a. Because ∆z has changed, we can solve eq. (13.5) for the radius of curvature needed to maintain ζp.b = ζp.a.
\(\ \begin{align} R_{b}=\frac{-M}{f_{c . a} \cdot\left(\Delta z_{m t n} / \Delta z_{T, a}\right)}\tag{13.7}\end{align}\)
Namely, in eq. (13.5), when ∆z became smaller while fc was constant, M/R had to also become smaller to keep the ratio constant. But since M/R was initially zero, the new M/R had to become negative. Negative R means anticyclonic curvature.
As sketched in Fig. 13.20, such curvature turns the wind toward the equator. But equatorward-moving air experiences smaller Coriolis parameter, requiring that Rb become larger (less curved) to conserve ζp . Near the east side of the Rocky Mountains the terrain elevation decreases at point “c”, allowing the air thickness ∆z to increase back to its original value.
But now the air is closer to the equator where Coriolis parameter is smaller, so the radius of curvature Rc at location “c” becomes positive in order to keep potential vorticity constant. This positive vorticity gives that cyclonic curvature that defines the lee trough of the Rossby wave. As was sketched in Fig. 13.7, surface cyclogenesis could be supported just east of the lee trough.
Sample Application
Picture a scenario as plotted in Fig. 13.20, with 25 m s–1 wind at location “a”, mountain height of 1.2 km, troposphere thickness of 11 km, and latitude 45°N. What is the value of the initial potential vorticity, and what is the radius of curvature at point “b”?
Find the Answer
Given: M = 25 m s–1, ∆zmtn = 1.2 km, Rinitial = ∞, ∆zT = 11 km, ϕ = 45°N.
Find: ζp.a = ? m–1·s–1, Rb = ? km
Assumption: Neglect wind shear in the vorticity calculation.
Eq. (10.16) can be applied to get the Coriolis parameter fc = (1.458x10–4 s–1)·sin(45°) = 1.031x10–4 s–1
Use eq. (13.6):
\(\zeta_{p}=\frac{1.031 \times 10^{-4} \mathrm{s}^{-1}}{11 \mathrm{km}}=9.37 \times 10^{-9} \mathrm{m}^{-1} \mathrm{s}^{-1}\)
Next, apply eq. (13.7) to get the radius of curvature:
\(R_{b}=\frac{-(25 \mathrm{m} / \mathrm{s})}{\left(1.031 \times 10^{-4} \mathrm{s}^{-1}\right) \cdot(1.2 \mathrm{km} / 11 \mathrm{km})}=-2223 . \mathrm{km}\)
Check: Physics and units are reasonable.
Exposition: The negative sign for the radius of curvature means that the turn is anticyclonic (clockwise in the N. Hemisphere). Typically, the cyclonic trough curvature is the same order of magnitude as the anticyclonic ridge curvature. East of the first trough and west of the next ridge is where cyclogenesis is supported.
13.3.3. Lee-side Translation Equatorward
Suppose an extratropical cyclone (low center) is positioned over the east side of a north-south oriented mountain range in the Northern Hemisphere, as sketched in Fig. 13.21. An example is the Rocky Mountains. In this diagram, the green circle and the air above it are the cyclone. Air within this cyclone has positive (cyclonic) vorticity, as represented by the rotating blue air columns in the figure. The locations of these columns are also moving counterclockwise around the common low center (L) — driven by the synoptic-scale circulation around the low.
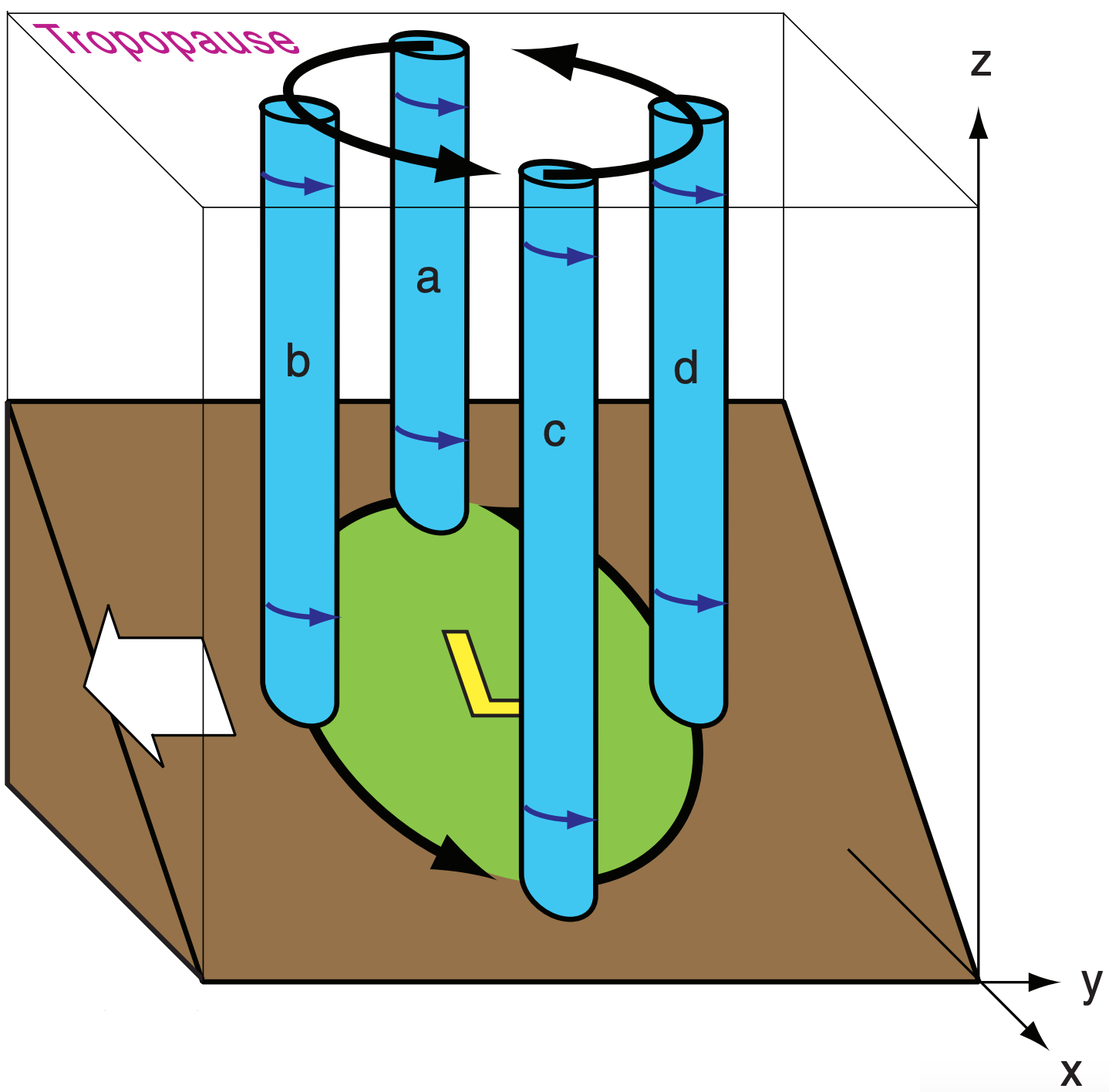
As column “a” moves to position “b” and then “c”, its vertical extent ∆z stretches. This assumes that the top of the air columns is at the tropopause, while the bottom follows the sloping terrain. Due to conservation of potential vorticity ζp, this stretching must be accompanied by an increase in relative vorticity ∆ζ r :
\(\ \begin{align} \Delta \zeta_{r}=2 \cdot R \cdot \alpha \cdot \zeta_{p}\tag{13.8}\end{align}\)
R is cyclone radius and α = ∆z/∆x is terrain slope.
Conversely, as column “c” moves to position “d” and then “a”, its vertical extent shrinks, forcing its relative vorticity to decrease to maintain constant potential vorticity. Hence, the center of action of the low center shifts (translates) equatorward (white arrow in Fig. 13.21) and downslope (eastward, in this example), following the region of increasing ζr .
A similar conclusion can be reached by considering conservation of isentropic potential vorticity (IPV). Air in the bottom of column “a” descends and warms adiabatically en route to position “c”, while there is no descent warming at the column top. Hence, the static stability of the column decreases at its equatorward and downslope sides. This drives an increase in relative vorticity on the equatorward and east flanks of the cyclone to conserve IPV. Again, the cyclone moves equatorward and eastward toward the region of greater ζ r .
Sample Application
The cyclone of Fig. 13.21 has ζp = 1x10–8 m–1·s–1 and R = 600 km. The mountain slope is 1:500. Find the relative-vorticity change on the equatorward side.
Find the Answer
Given: ζp = 1x10–8 m–1·s–1, R = 600 km, α = 0.002
Find: ∆ζr = ? s–1 .
Assume constant latitude in Northern Hemisphere.
Use eq. (13.8):
∆ζr = 2 · (600,000 m) · (0.002) · (1x10–8 m–1·s–1) = 2.4x10–5 s–1 .
Check: Physics and units are reasonable
Exposition: A similar decrease is likely on the poleward side. The combined effect causes the cyclone to translate equatorward to where vorticity is greatest.


