11.12: Three-band Global Circulation
- Page ID
- 10213
In the chapter introduction, it was stated that Coriolis force causes the thermally-driven planetary circulation to break down into 3 latitude-bands (Fig. 11.58) in each hemisphere. These bands are: (1) a strong, direct, asymmetric, vertical-circulation Hadley cell in low latitudes (0° - 30°); (2) a band of mostly horizontal Rossby waves at mid-latitudes (30° - 60°); and a weak direct vertical circulation cell at high latitudes (60° to 90°). Fig. 11.58 includes more (but not all) of the details and asymmetries explained in this chapter.
The circulation bands work together to globally transport atmospheric heat (Fig. 11.14), helping undo the differential heating that was caused by solar and IR radiation. The Earth-atmosphere-ocean system is in near equilibrium thermally, with only extremely small trends over time related to global warming.
The circulation bands also work together in the meridional transport of zonal momentum. The trade winds, blowing opposite to the Earth’s rotation, exert a torque (force times radius) that tends to slow the Earth’s spin due to frictional drag against the land and ocean surface. However, in mid-latitudes, the westerlies dragging against the Earth’s surface and against mountains apply an opposite torque, tending to accelerate the Earth’s spin. On the long term, the opposite torques nearly cancel each other. Thus, the whole Earth-atmosphere-ocean system maintains a near-equilibrium spin rate.
During high-wind episodes in one of the circulation bands, temporary changes in wind-drag torques are large enough to make measurable changes in the Earth’s rotation rate — causing the length of a day to increase or decrease 1 - 3 µs over periods of months. In addition, external influences (lunar and solar tides, solar wind, geomagnetic effects, space dust) cause the Earth to spin ever more slowly, causing the length of a day to increase 1.4 ms/century at present.
11.12.1. A Metric for Vertical Circulation
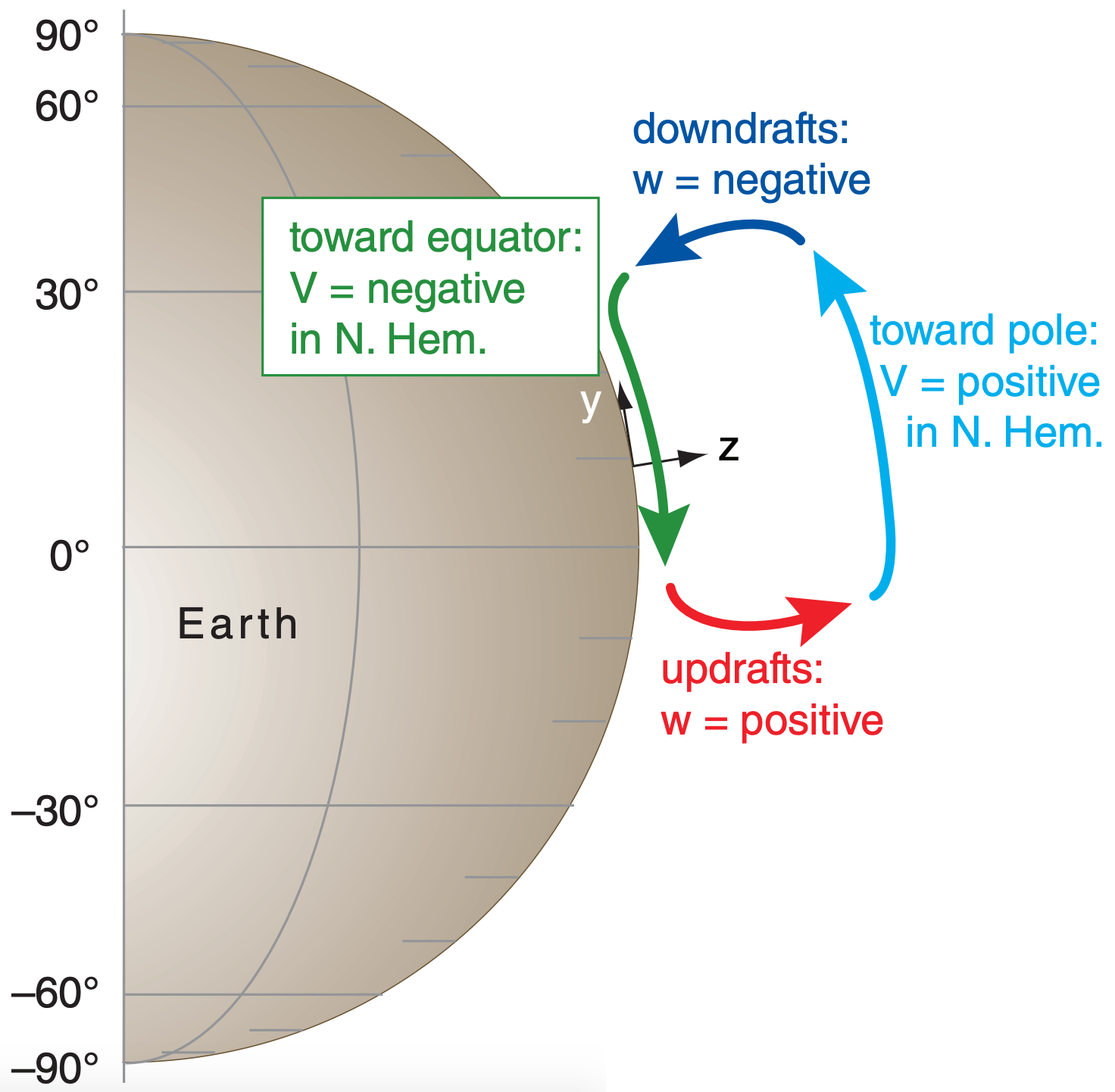
Getting back to atmospheric circulations, one can define the strength CC of a vertical circulation cell as:
\(\ \begin{align} C C=\left[\frac{f_{c}^{2}}{N_{B V}^{2}} \frac{\Delta V}{\Delta z}\right]-\frac{\Delta w}{\Delta y}\tag{11.50}\end{align}\)
Direct circulation cells are ones with a vertical circulation in the direction you would expect if there were no Coriolis force. The units for circulation are s–1.
Using the major Hadley cell as an example of a direct circulation (Fig. 11.59), note that w decreases as y increases; hence, ∆w/∆y is negative. Similarly, ∆V/∆z is positive. Thus, eq. (11.50) gives a positive CC value for direct circulations, and a negative value for indirect circulations (having an opposite rotation direction).
11.12.2. Effective Vertical Circulation
When the forecast equations for momentum and heat are applied to eq. (11.50), the result allows you to anticipate the value of CC for a variety of situations— even situations where vertical cells are not dominant:
\(\ \begin{align} C C \propto-\frac{\Delta E_{n e t}}{\Delta y}+\operatorname{Curv}\left(F_{y} w a v e\right)+\frac{\Delta M G}{\Delta z}\tag{11.51}\end{align}\)
circulation radiation \(\quad\) wave-heat \(\quad\) wave-momentum
In this equation are factors and terms that were discussed earlier in this chapter. For example, you can use Fig. 11.10 to estimate Enet, the differential heating due to radiation, and how it varies with y. The sign of the curvature (Curv) of the Rossby-wave heat flux Fy wave was shown in Fig. 11.55. If we assume that the meridional gradient of zonal momentum MG ≈ 0 near the ground, then ∆MG/∆z has the same sign as MG, as was sketched in Fig. 11.57.
With this information, you can estimate the sign of CC in different latitude bands. Namely, you can anticipate direct and indirect circulations. For the Northern Hemisphere, the results are:
circulation ∝ radiation + wave-heat + wave-momentum = total
CCpolar ∝ positive + positive + positive = positive
CCmidlat ∝ positive + negative +negative = negative
CCtropics∝ positive + positive + positive = positive
Sample Application
Suppose the Hadley cell updraft and downdraft velocities are 6 and –4 mm s–1, respectively, and the meridional wind speeds are 3 m s–1 at the top and bottom of the cell. The major Hadley cell is about 17 km high by 3900 km wide, and is centered at about 10° latitude. Temperature in the tropical atmosphere decreases from about 25°C near the surface to –77°C at 17 km altitude. Find the vertical cell circulation.
Find the Answer
Given: ∆w = –10 mm s–1 = –0.01 m s–1 , ∆y = 3.9x103 km
∆V = 6 m s–1, ∆z = 17 km, ϕ = 10°, ∆T = –102°C.
Find: CC = ? s–1.
First, use eq. (10.16):
fc = (1.458x10–4 s–1)·sin(10°) = 2.53x10–5 s–1
Next, for the Brunt-Väisälä frequency, we first need:
Tavg = 0.5*(25 – 77)°C = –26°C = 247 K
In the tropics ∆T/∆z = –6 °C km–1 = –0.006 K m–1
Then use eq. (5.4), and assume Tv = T:
\(N_{B V}=\sqrt{\frac{9.8 \mathrm{m} / \mathrm{s}^{2}}{247 \mathrm{K}}(-0.006+0.0098) \frac{\mathrm{K}}{\mathrm{m}}}=0.0123 \mathrm{s}^{-1}\)
Finally, use eq. (11.50):
\(C C=\left[\left(\frac{2.53 \times 10^{-5} \mathrm{s}^{-1}}{0.0123 \mathrm{s}^{-1}}\right)^{2} \cdot \frac{6 \mathrm{m} / \mathrm{s}}{17000 \mathrm{m}}\right]-\frac{-0.01 \mathrm{m} / \mathrm{s}}{3.9 \times 10^{6} \mathrm{m}}\)
CC = 1.493x10–9 + 2.564x10–9 s–1 = 4.06x10–9 s–1
Check: Physics & units are reasonable.
Exposition: Both terms contribute positively to the circulation of the major Hadley cell during Northern Hemisphere winter.
Rossby waves so efficiently transport heat and momentum at midlatitudes that the effective vertical circulation is negative. This indirect circulation is called the Ferrel cell.
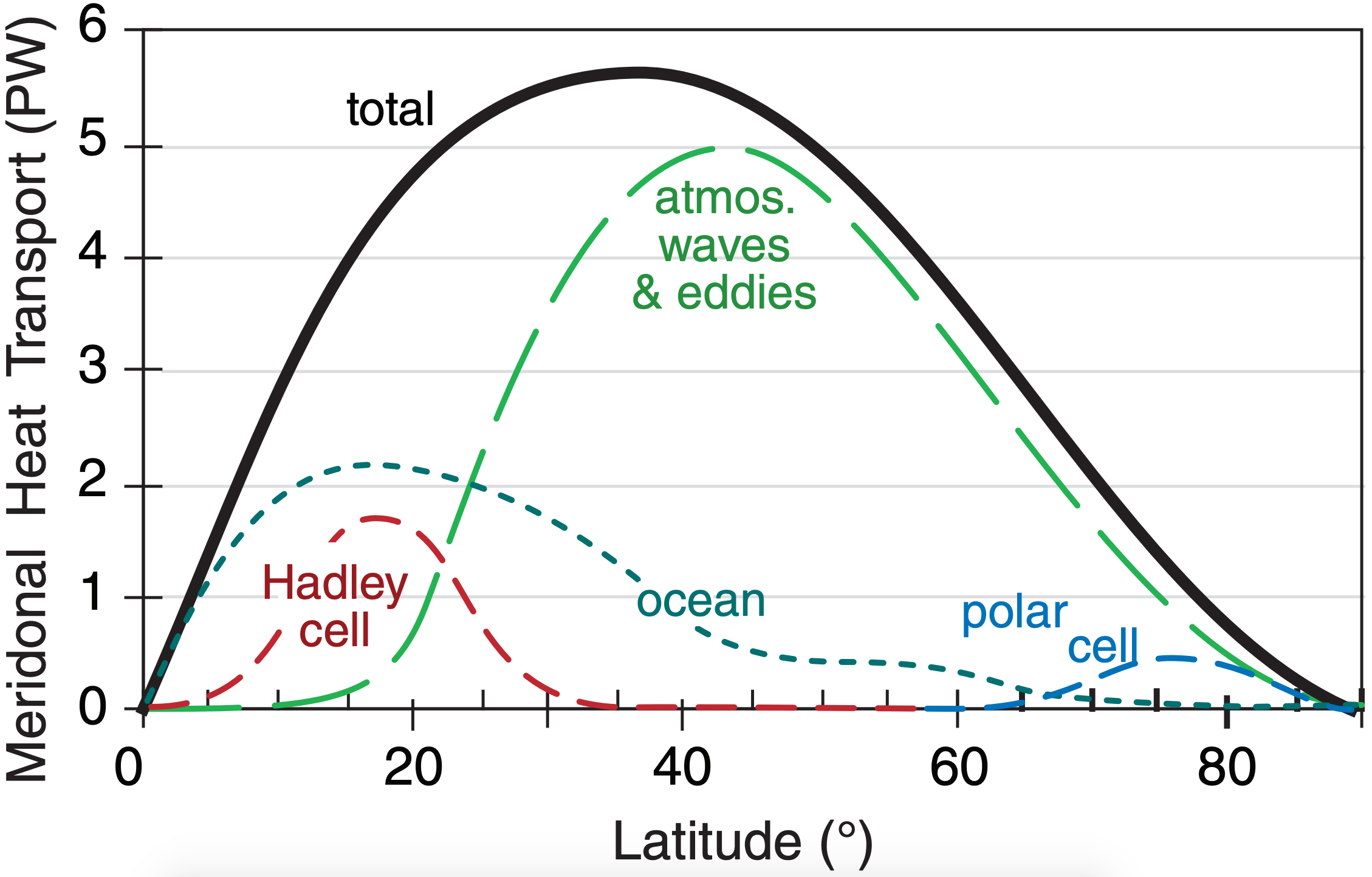
Fig. 11.60 redraws the N. Hemisphere portion of Fig. 11.14, qualitatively highlighting the relative contributions of the direct (Hadley and polar cells) and indirect (Ferrel cell/Rossby waves) atmospheric circulations to the total meridional heat transport. At mid-latitudes, the main circulation feature is the Rossby-wave meanders of the jet stream near the tropopause, and the associated low- and high-pressure centers near the surface. High- and low-latitudes are dominated by direct vertical circulations.
Ocean currents also contribute to global heat redistribution. Although ocean-circulation details are not within the scope of this book, we will introduce one ocean topic here — the Ekman spiral. This describes how wind drag can drive some ocean currents, including hurricane storm surges.


