7.5: Ice Growth by Diffusion
- Page ID
- 9572
7.5.1. Ice Crystal Habits
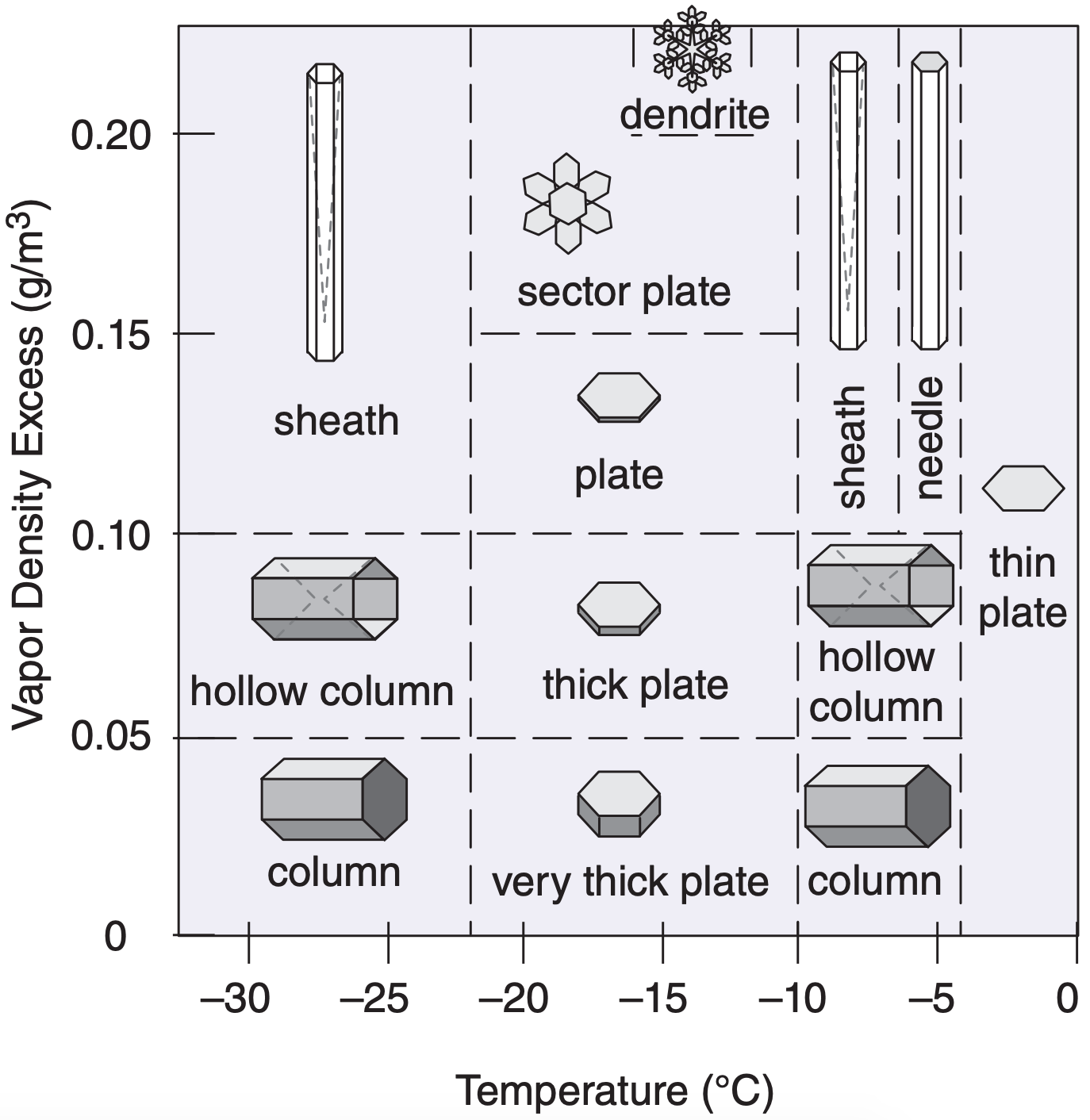
In the troposphere, the normal ice crystal shape that forms from direct deposition of water vapor is hexagonal (see INFO Box at left). The particular hexagonal shape that grows depends on temperature and supersaturation (Fig. 7.12). These shapes are called habits. Supersaturation is sometimes given as water-vapor density excess ρve = ρv – ρvs, where ρv is absolute humidity and ρvs is the saturation value of absolute humidity.
As ice crystals fall and move by wind and turbulence, they pass through regions of different temperature and vapor-density excess in the cloud. This allows individual crystals to grow into complex combinations of habits (Fig. 7.13). For example, a crystal that starts growth as a column might later be capped on each end by large plates. Because each crystal travels through a slightly different path through the cloud, each snowflake has a unique shape.

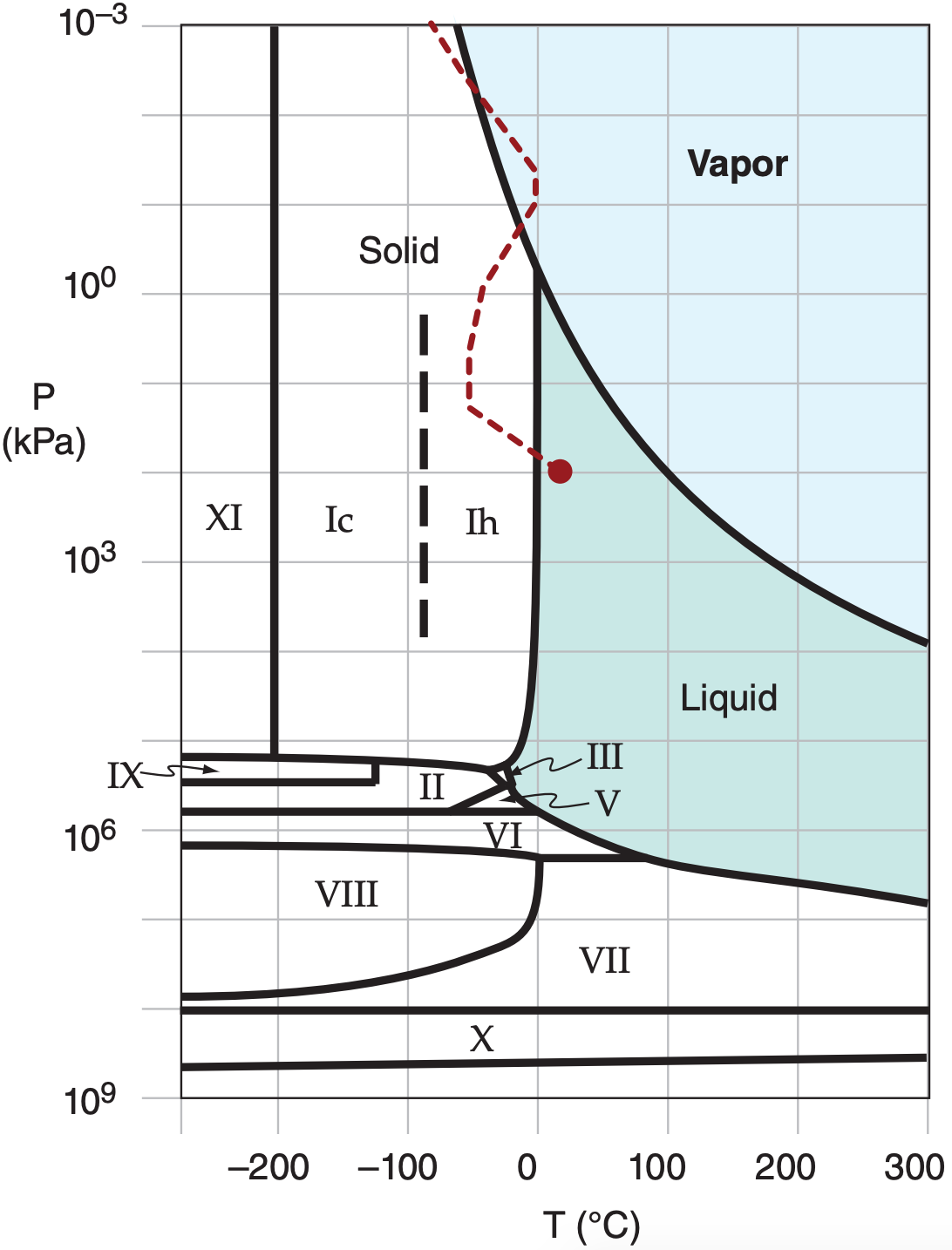
Fourteen phases of ice have been identified, and are labeled using Roman numerals I–XIV (see Fig. 7.b). More phases might be discovered in the future. Each phase is a preferred arrangement of molecules having uniform chemical composition and physical state.
At normal atmospheric temperatures and pressures, ice I is most prevalent. However, it comes in two variants: hexagonal ice (Ih), and cubic ice (Ic). Ice Ih is the form that is thermodynamically stable in the troposphere. Both forms of ice I have a tetrahedral arrangement of water molecules.
Hexagonal ice Ih forms crystals that are hexagonal plates, hexagonal columns with flat ends, hexagonal columns with pyramidal ends, and dendrites (snowflakes with 6 arms). Samples of these crystal shapes have been collected in the atmosphere, and are frequently observed. This is the normal ice that we see.
Cubic ice Ic is believed to be able to form as cubes, square columns capped by pyramids, and octahedrons (equal to two pyramids with their bases merged). Natural crystals of ice Ic have been detected in the lower stratosphere, but never been successfully captured in the lower troposphere partly because it is metastable with respect to ice Ih, and at warmer temperatures ice Ic rapidly converts to Ih. Cubic ice has been created in the lab under atmospheric conditions, and its existence in the atmosphere has been inferred from certain halos observed around the sun (because ice crystals act like prisms; see the Optics chapter).
Snow avalanches are often associated with weak snow layers buried under stronger layers of snow. Field observations of snow crystal shape and size are important for detecting the different snow layers. The International Commission on Snow and Ice (ICSI) developed in 1990 a standard symbology (Table 7-A & Table 7-B) to use when logging snow data.
|
Table 7-A. Morphological (shape-based) classification of precipitation particles. T = temperature, ρve = excess water vapor density. [Colbeck et al, 1990: The International Classification for Seasonal Snow on the Ground, ICSI. 37pp. Available from http://www.crrel.usace.army.mil/techpub/ CRREL_Reports/reports/Seasonal_Snow.pdf ] |
|||
| Name | Symbol | Shape & Formation | |
|---|---|---|---|
| 1a | Columns |  |
Short, prismatic crystal, solid or hollow. See Fig. 7.12 for T & ρve conditions. |
| 1b | Needles |  |
Needle-like, approximately cylindrical. See Fig. 7.12 for T & ρve conditions. |
| 1c | Plates |  |
Plate-like, mostly hexagonal. See Fig. 7.12 for T & ρve conditions. |
| 1d | Stellars, Dendrites |  |
Six-fold star-like, planar or spatial. See Fig. 7.12 for T & ρve conditions. |
| 1e | Irregular Crystals | 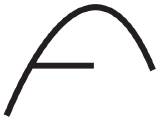 |
Clusters of very small crystals. Polycrystals growing at varying environmental conditions. |
| 1f | Graupel | 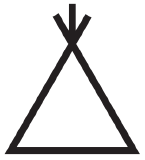 |
Heavily rimed particles. Caused by accretion of supercooled water. |
| 1g | Hail |  |
Laminar internal structure, translucent or milky, glazed surface. Growth by accretion of supercooled water. |
| 1h | Ice Pellets |  |
Transparent, mostly small spheroids. Frozen rain. |
| Table 7-B. Snow-grain classification (ICSI). | |
| Term | Size (mm) |
|---|---|
| Very fine | < 0.2 |
| Fine | 0.2 to 0.5 |
| Medium | 0.5 to 1.0 |
| Coarse | 1.0 to 2.0 |
| Very coarse | 2.0 to 5.0 |
| Extreme | > 5.0 |
7.5.2. Growth Rates
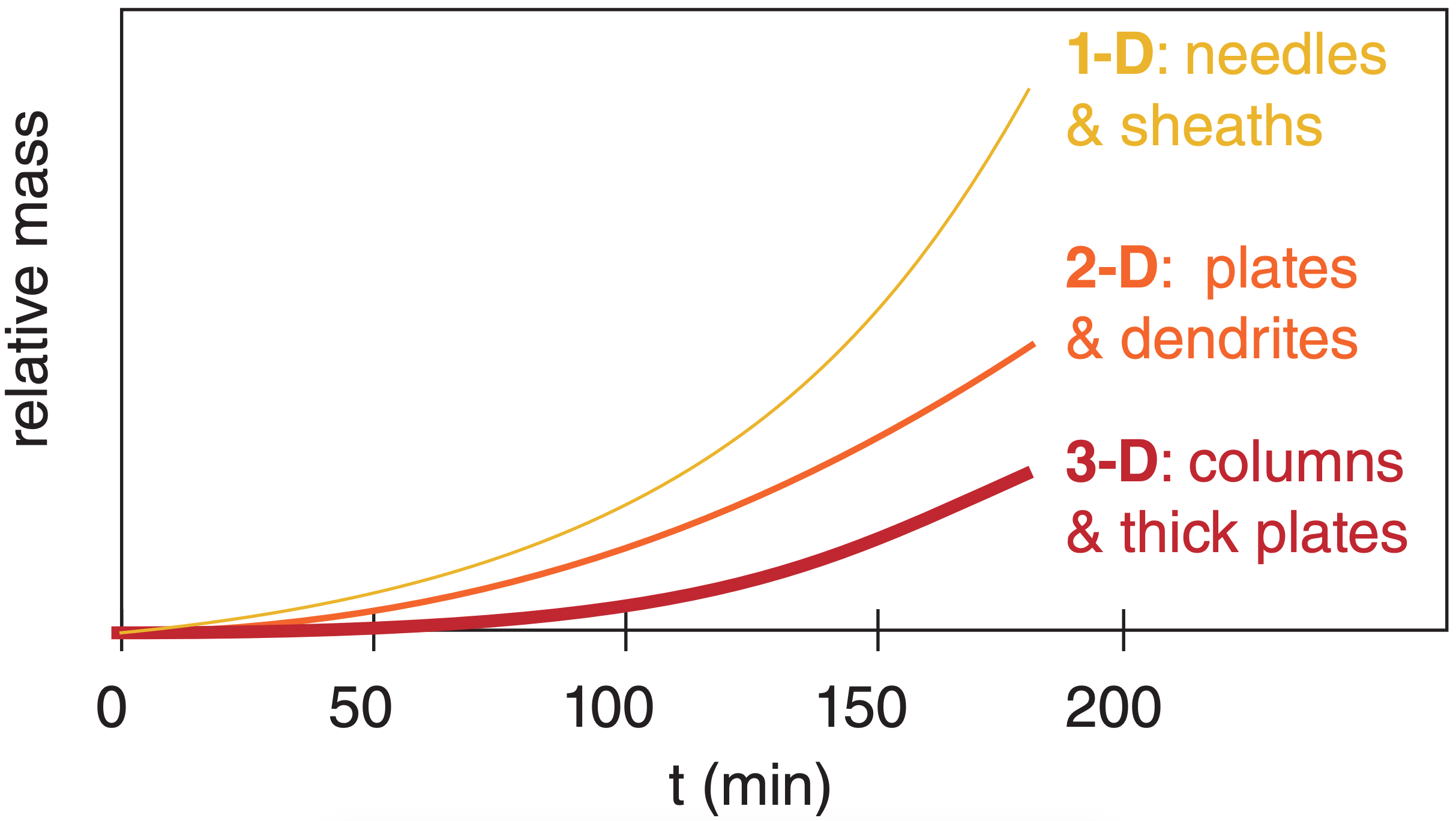
Because of the diversity of shapes, it is better to measure crystal size by its mass m rather than by some not-so-representative radius. Rate of growth by diffusion depends on crystal habit.
Columns and very thick plates have an aspect ratio (height-to-width ratio) of roughly 1. If the aspect ratio remains constant during growth, then the growth equation is:
\(\ \begin{align} m \approx c_{3} \cdot\left(\rho_{v}^{3} / \rho_{i}\right)^{1 / 2} \cdot[D \cdot S \cdot t]^{3 / 2}\tag{7.26}\end{align}\)
where c3 = 11.85 (dimensionless), ρv is the density of water vapor (=absolute humidity, see eq. 4.10), ρi is ice density (= 916.8 kg m–3 at 0°C), D is diffusivity, S is supersaturation fraction, and t is time. If the crystal were spherical with radius R, then its mass would be m = ρliq.water · (4·π/3)·R3. Taking the cube root of both sides of eq. (7.26) gives an equation similar to eq. (7.24). Thus growth rate of a 3-D crystal is very similar to growth of a liquid droplet.
For 2-D growth, such as dendrites or plates of constant thickness d, the growth equation changes to
\(\ \begin{align} m \approx \frac{c_{2}}{d} \cdot\left(\frac{\rho_{v}^{2}}{\rho_{i}}\right) \cdot[D \cdot S \cdot t]^{2}\tag{7.27}\end{align}\)
where c2 = 5.09 (dimensionless). For 1-D growth of needles and sheaths of constant diameter, the growth equation is
\(\ \begin{align} m \propto \exp \left[(D \cdot S \cdot t)^{1 / 2}\right]\tag{7.28}\end{align}\)
These three growth rates are sketched in Fig. 7.14.
Evidently 2-D crystals increase mass faster than 3-D ones, and 1-D crystals increase mass faster still. Those crystals that gain the mass fastest are the ones that will precipitate first.
Sample Application
Given a mixed-phase cloud (i.e., having both ice crystals and supercooled liquid water droplets) at –14°C that is saturated with respect to water (and thus supersaturated with respect to ice; see Fig. 4.2 in the Water Vapor chapter). If the water vapor diffusivity is 1.5x10–5 m2 s–1, then what is the relative mass of ice crystals after 1 hour of growth, for (a) a 3-D crystal and (b) a 2-D crystal that is 15 µm thick?
Find the Answer
Given: D = 1.5x10–5 m2 s–1, t = 1 h = 3600 s, T = 259K
d = 15 µm = 1.5x10–5 m.
Find: m = ? kg
Assume: initial mass m is negligible
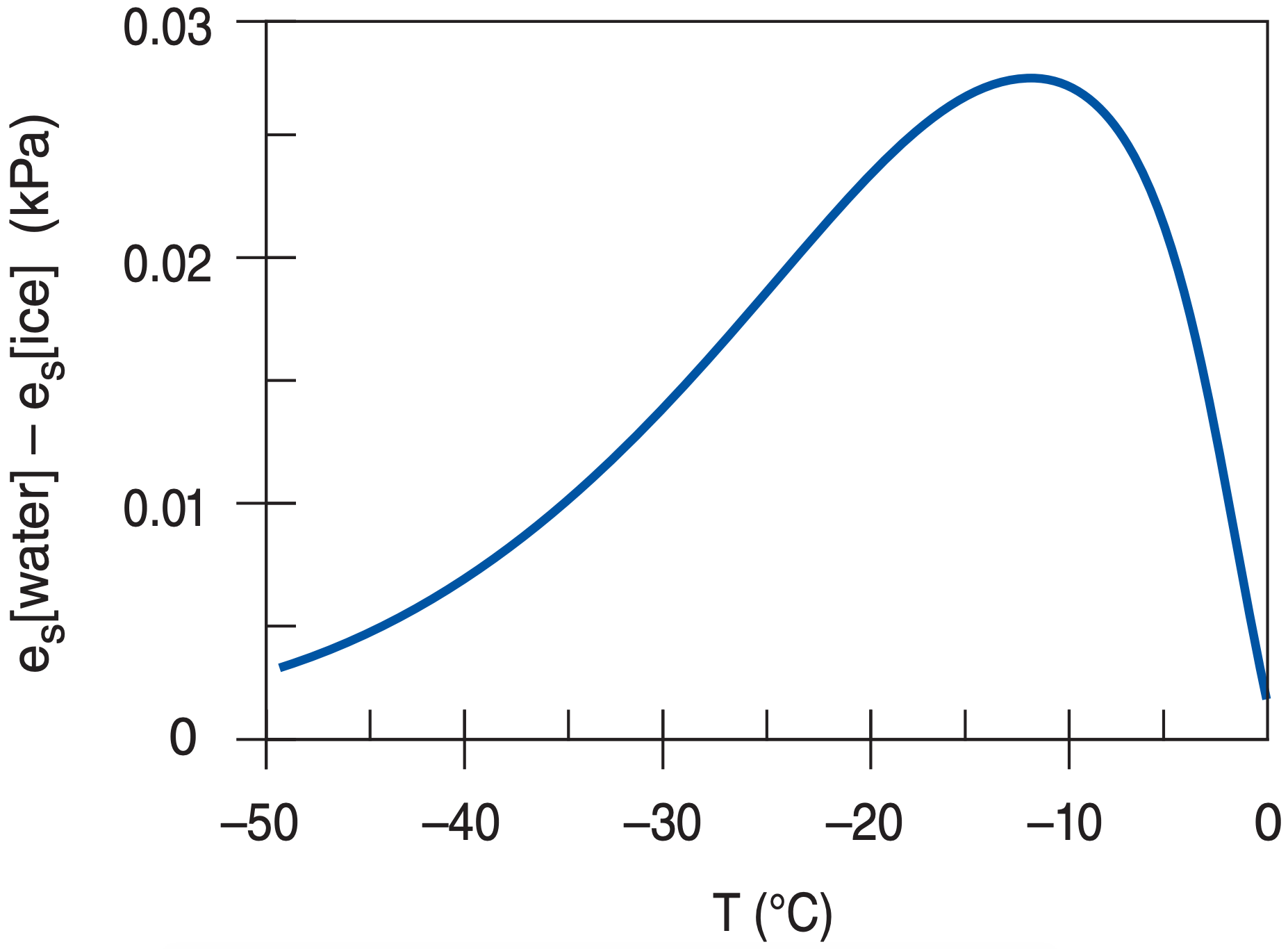
First, use Fig. 4.2 in the Water Vapor chapter to estimate the supersaturation. The insert in that fig. shows that (ewater – eice ) ≈ 0.0275 kPa at T = –14°C, and eice ≈ 0.175 kPa. The supersaturation is:
S = (ewater – eice ) / eice = (0.0275 kPa)/(0.175 kPa)
S = 0.157 (dimensionless)
Use the ideal gas law for water vapor (eq. 4.10) to estimate vapor density from vapor pressure (which for this case equals ewater ≈ 0.20 kPa, from previous paragraph):
ρv = ewater/(ℜv·T) = = (0.2 kPa) /[(0.461 kPa·K–1·m3·kg–1)·(259 K)] = 1.68 x 10–3 kg m–3
(a) Use eq. (7.26). The factor in parenthesis is
(ρv3/ρi )1/2 = [(1.68x10–3 kg m–3)3/(916.8 kg m–3)]1/2 = 2.27x10–6 kg m–3
and the term in square brackets of eq. (7.26) is
[ ] = [(1.5x10–5 m2 s–1)·(0.157)·(3600s)]3/2
[ ] = (8.478x10–3 m2)3/2 = 7.8x10–4 m3
Thus, solving eq. (7.26):
m = 11.85·(2.27x10–6 kg m–3)·(7.8x10–4 m3)
= 2.1x10–8 kg = 2.1x10–5 g
(b) Use eq. (7.27):
\(\begin{aligned} m &=\frac{5.09}{1.5 \times 10^{-5} \mathrm{m}} \cdot\left(\frac{\left(0.00168 \mathrm{kg} / \mathrm{m}^{3}\right)^{2}}{916.8 \mathrm{kg} / \mathrm{m}^{3}}\right) \cdot\left[8.478 \times 10^{-3} \mathrm{m}^{2}\right]^{2} =7.51 \times 10^{-8} \mathrm{kg}=7.51 \times 10^{-5} \mathrm{g} \end{aligned}\)
Check: Units OK. Physics OK. Agrees with Fig. 7.14.
Exposition: Typically observed ice-crystal mass is about 3x10–5 g. Typical snowflakes that fall to Earth are often aggregates of hundreds of ice crystals stuck together, with a total mass of about 3 mg snowflake–1.
7.5.3. The Wegener-Bergeron-Findeisen (WBF) Process
Recall from the Water Vapor chapter that ice has a lower saturation vapor pressure than liquid water at the same temperature. Fig. 7.15 shows an enlargement of the saturation vapor-pressure curves for liquid water and ice.
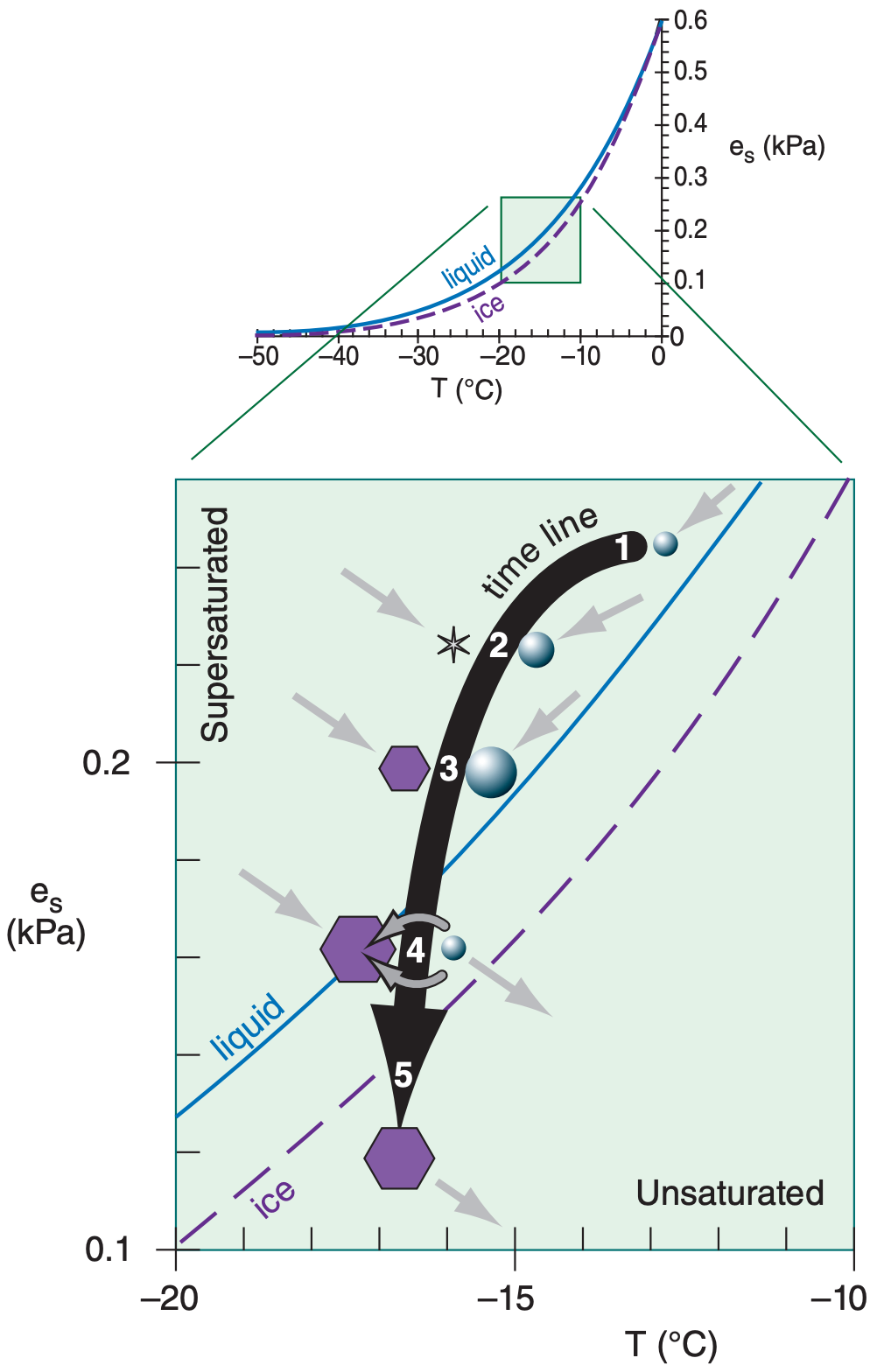
Suppose that initially (time 1, on the time line in Fig. 7.15) there are only supercooled liquid water droplets in a cloudy air parcel. These droplets exist in a supersaturated environment and therefore grow as the excess water vapor diffuses toward the droplets. As the air parcel rises and cools within the cloud, some ice nuclei might become activated at time 2, causing ice crystals to form and grow. The excess water vapor now deposits on both the liquid and solid hydrometeors.
Both the ice crystals and liquid droplets continue to grow, because both are in a supersaturated environment (time 3). However, the ice crystal grows a bit faster because it is further from its ice saturation line (i.e., more supersaturated) than the liquid droplet is from liquid saturation line.
As both hydrometeors grow, water vapor is removed from the air, reducing the supersaturation. Eventually, near point 4 on the time line, so much vapor has been consumed that the relative humidity has dropped below 100% with respect to liquid water. Hence, the liquid droplet begins to evaporate into the unsaturated air. However, at point 4 the ice crystal continues to grow because the air is still supersaturated with respect to ice.
The net result is that the ice crystals grow at the expense of the evaporating liquid droplets, until the liquid droplets disappear (point 5). This is called the Wegener-Bergeron-Findeisen (WBF) process.
The difference between ice and liquid saturation vapor pressures is greatest in the range –8°C to –16°C, as shown in Fig. 7.16 (from the insert in Fig. 4.2). This is the temperature range where we expect the maximum effect from the WBF growth process, also known as the cold-cloud process because temperatures below freezing are needed.
If a large number of ice nuclei exist in the air, then a large number of ice crystals will form that are each too small to precipitate. For a very small number of ice nuclei, those few ice crystals will rapidly grow and precipitate out, leaving behind many small liquid cloud droplets in the cloud. Both of these scenarios lead to relatively little precipitation.
Only with a medium concentration (1 to 10) ice nuclei per liter (compared to about a million liquid droplets in the same volume) will the ice nuclei be able to scavenge most of the condensed water before precipitating out. This scenario causes the maximum precipitation for the WBF processes. But a restriction on this precipitation formation process is that it happens only in cold clouds (clouds colder than 0°C).
As was discussed in the nucleation sections, there are indeed fewer ice nuclei than CCN, hence the cold-cloud process can be an important first step in getting hydrometeors large enough to begin to fall out of the cloud as precipitation.
The cold-cloud process can occur even in summer, but higher in the troposphere where the air is colder. As these ice particles fall into warmer air at lower altitude, they melt into raindrops to create summer convective rain showers (see Fig. 7.21 later in this chapter).


