7.2: Nucleation of Liquid Droplets
- Page ID
- 9569
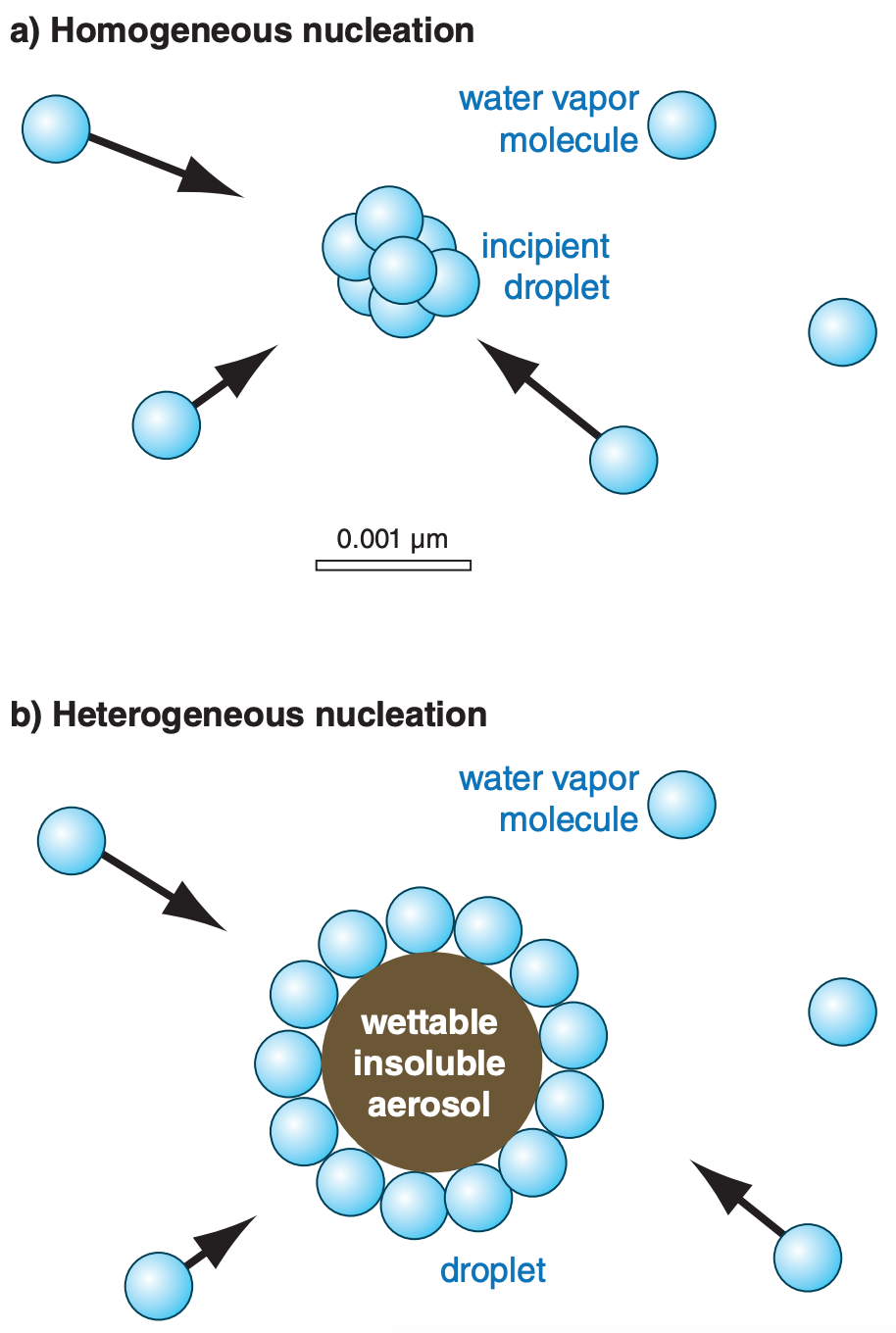
Nucleation (the creation of new droplets) in clean air is called homogeneous nucleation (Fig. 7.4a). We will show that homogeneous nucleation is virtually impossible in the real atmosphere and can be neglected. Nucleation of cloud droplets by water vapor condensing on tiny dust particles in the air is called heterogeneous nucleation (Fig. 7.4b). Even with heterogeneous nucleation, there is a barrier to droplet formation that must first be overcome.
7.2.1. Cloud Condensation Nuclei (CCN)
An aerosol is any tiny solid or liquid particle suspended in the air. The subset of aerosol particles that can nucleate cloud droplets are called cloud condensation nuclei (CCN). To nucleate a droplet, a solid aerosol either must be soluble in water (such as various salt particles), or be sufficiently large in diameter (radius > 0.1 µm) and have a wettable surface (i.e., be hydrophilic).
Boundary-layer air over oceans has smaller concentrations of aerosols than continental air. Over oceans, of the 150 to 1000 total aerosol particles cm–3 of air, only about 90 to 200 particles cm–3 are CCN at normal values of relative humidity (RH ≈ 101%) inside clouds. Over continents, of the 2,000 to 70,000 total aerosol particles cm–3 of air, only about 200 to 700 particles cm–3 are CCN. At higher relative humidities, larger percentages of aerosols act as CCN. Exceptionally clean air over the Arctic can have only 30 CCN particles cm–3, while over industrial cities the CCN count can approach 106 particles cm–3.
CCN particles can form when pollutant gases (of molecular size: 10–4 to 10–3 µm) in the air cluster to form ultrafine aerosols (size 10–3 to 10–2 µm) or are oxidized in the presence of sunlight. Over the oceans, sulfate and sulfuric acid CCN can form this way from gases such as dimethyl sulfide and methane sulfonic acid, produced by phytoplankton (microscopic drifting plant life in the ocean).
Further condensation of more pollutant gases and coagulation (sticking together) cause the aerosols to quickly grow to 0.01 to 1 µm size, called fine aerosols. Beyond this size range they grow more slowly. As a result, aerosols in this size range tend to accumulate — a process called accumulation mode. At larger 1 to 10 µm sizes, coarse mode CCN can form by other processes, such as strong winds that pick up fine dirt from the ground.
Small nuclei are much more abundant than larger ones (thin wiggly line in Fig. 7.5). Instead of a smooth decrease in number of particles as their size increases, the aerosol curve often has two or three peaks corresponding to the ultrafine, accumulation, and coarse modes.
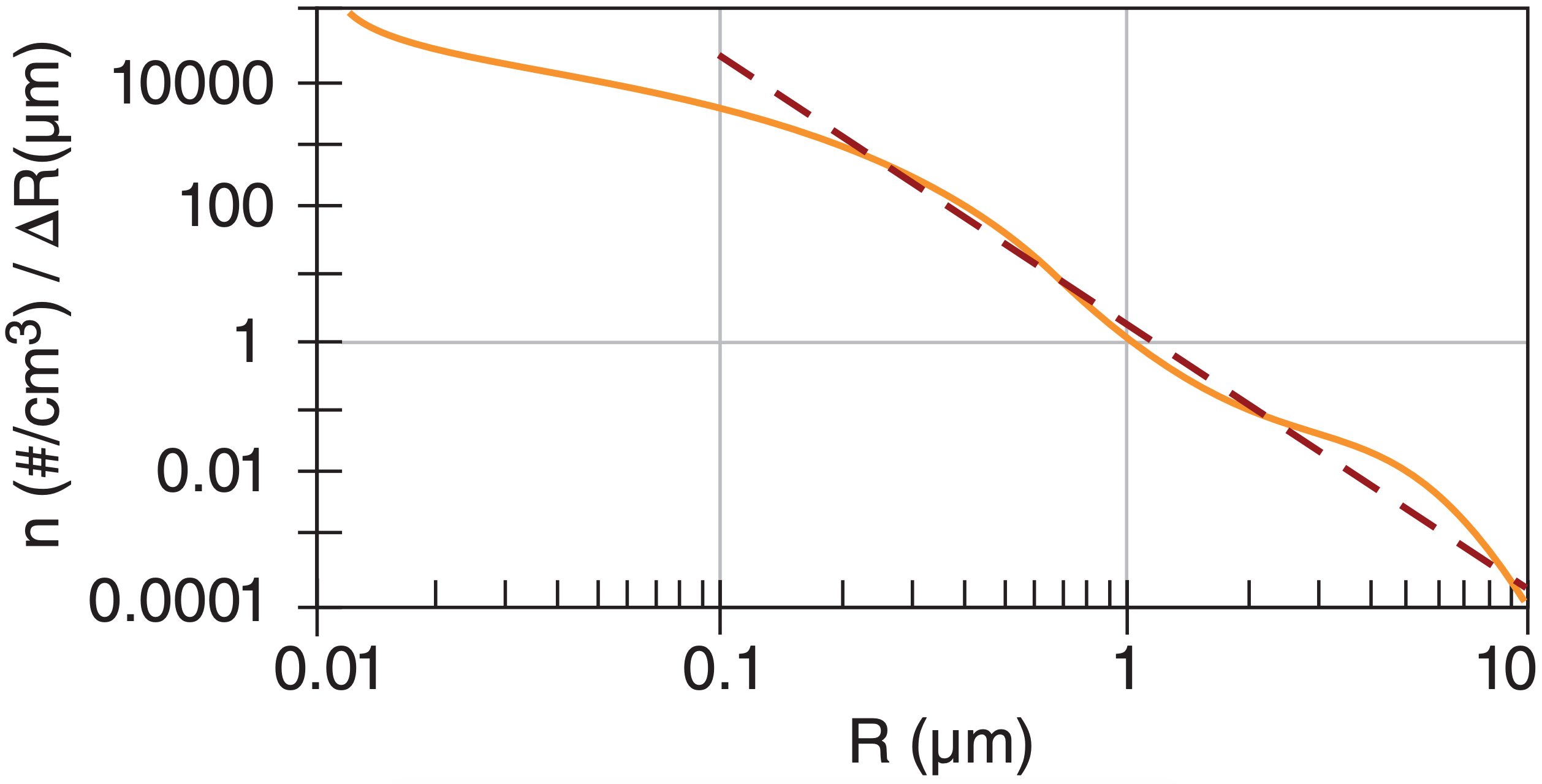
Over continental regions, the number density (n = count of particles per volume of air) of particles with radius between R – 0.5·∆R and R + 0.5·∆R can be approximated by:
\(\ \begin{align} n(R)=c \cdot R^{-4} \cdot \Delta R\tag{7.9}\end{align}\)
for particles larger than 0.2 µm, and for small ∆R. Constant c depends on the total concentration of particles. This distribution, called the Junge distribution, is the dashed straight line in Fig. 7.5.
Sample Application
If c = 5x107 µm3·m–3 for the Junge distribution, then how many CCN are expected within radii ranges of (a) 0.45 - 0.55 µm and (b) 0.95 - 1.05 µm?
Find the Answer
Given: R = 0.5 µm & 1.0 µm, ∆R= 0.1 µm for both ranges, and c = 5x107 µm3·m–3
Find: n = ? # m–3
Use eq. (7.9):
a) n = (5x107µm3·m–3)·(0.5 µm)–4 ·(0.1µm) = 8 x 107 m–3.
(b) n = (5x107 µm3·m–3)·(1 µm)–4 ·(0.1 µm) = 5 x 106 m–3.
Check: Units OK. Physics OK.
Exposition: Doubling the particle radius reduces the number density by more than tenfold. If each CCN nucleates a cloud droplet, then each m3 of cloudy air contain tens of millions of cloud droplets. Concentrations in real clouds can be 10s to 1000s of times greater.
7.2.2. Curvature and Solute Effects
Both droplet curvature and chemical composition affect the evaporation rate, which affect the fate of the droplet.
7.2.2.1. Curvature Effect
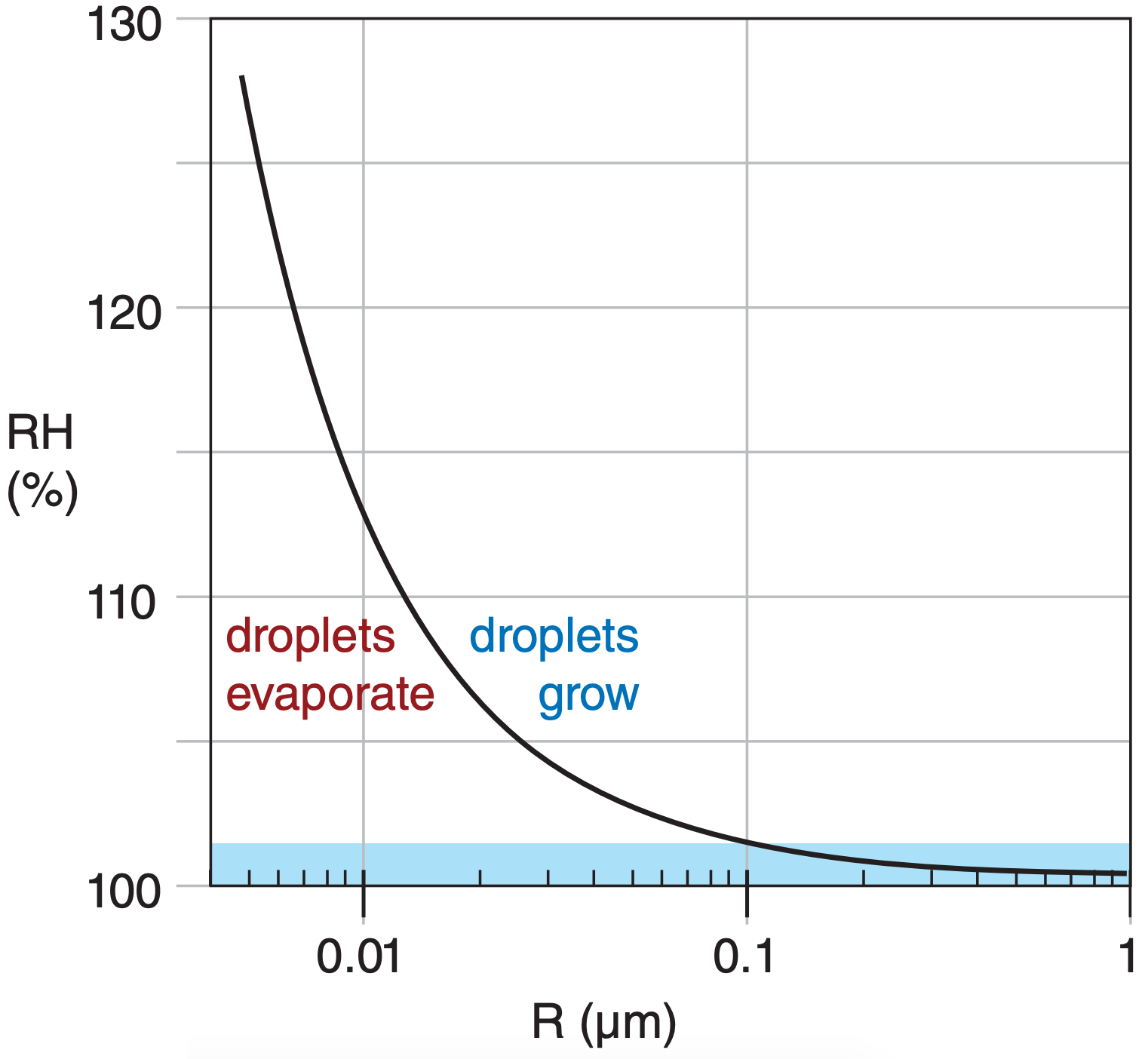
The evaporation rate from the curved surface of a droplet is greater than that from a flat water surface, due to surface tension. But droplet growth requires condensation to exceed evaporation. Thus, to be able to grow, smaller droplets need greater RH in the air than larger drops. The resulting equilibrium RH in the air as a function of droplet radius R is described by Kelvin’s equation
\(\ \begin{align} R H \%=100 \% \cdot \exp \left[\frac{2 \cdot \sigma}{\rho_{m} \cdot k_{B} \cdot T \cdot R}\right]\tag{7.10a}\end{align}\)
where σ = 0.076 N m–1 is surface tension of pure water at 0°C, ρm = 3.3x1028 molecules m–3 is the number density of water molecules in liquid at 0°C, kB = 1.38x10–23 J·K–1·molecule–1 is Boltzmann’s constant, and T is absolute temperature (in Kelvin) of the droplet. Kelvin’s equation can be abbreviated as
\(\ \begin{align} R H \%=100 \% \cdot \exp \left[\frac{c_{1}}{T \cdot R}\right]\tag{7.10b}\end{align}\)
where c1 = 0.3338 µm·K = 2σ/(ρm·kB).
Fig. 7.6 illustrates the curvature effect described by Kelvin’s equation, where conditions above the line allow droplets to grow. For example, droplets of radius smaller than 0.005 µm need an environment having RH > 128% to grow. But larger droplets of radius 0.1 µm need only RH > 101% to grow.
Sample Application
What humidity in a cloud at 0°C is needed to allow a droplet of radius 0.03 µm to grow?
Find the Answer
Given: R = 0.03 µm. T = 273 K
Find: RH = ? %
Use eq. (7.10b) RH% = 100% · exp[(0.334 µm·K) / (273K · 0.03 µm)] = 104.16%
Check: Units OK. Magnitude OK.
Exposition: A stable droplet this small is unlikely in a real cloud, where typically RH ≈ 101% or less.
For homogeneous nucleation in clean air (no aerosols), incipient droplets form when several water-vapor molecules merge (Fig. 7.4a). The resulting droplet has extremely small radius (≈0.001 µm), causing it to evaporate quickly, given the typical humidities in clouds of ≈101% (grey shaded band in Fig. 7.6). How ever, for heterogeneous nucleation the small number of water molecules can coat the outside of the aerosol particle (Fig. 7.4b), with a resulting radius that is relatively large. Droplets formed by heterogeneous nucleation grow and remove water-vapor molecules from the air, thereby lowering the RH and eliminating the chance for homogeneous nucleation.
7.2.2.2. Solute Effect
Solutions (i.e., water containing dissolved chemicals) evaporate water molecules at a slower rate than does pure water. Solutions occur when condensation occurs on impurities such as certain cloud condensation nuclei (CCN) that dissolve in the nascent water droplet. This can partially compensate the curvature effect.
Recall that the saturation vapor pressure es over a flat surface of pure water was given in the Water Vapor chapter by the Clausius-Clapeyron equation. The two opposing effects of curvature and solute can be combined into one equation (Köhler equation) for the ratio of actual saturation vapor pressure es* in equilibrium over a solution with a curved surface, to vapor pressure over a flat surface of pure water es:
\(\ \begin{align} R H=\frac{e_{S}^{*}}{e_{S}} \approx \frac{\exp \left(\frac{c_{1}}{T \cdot R}\right)}{1+\frac{c_{2} \cdot i \cdot m_{S}}{M_{s} \cdot R^{3}}}\tag{7.11}\end{align}\)
where RH is the relative humidity fraction, T is absolute temperature, R is drop radius, i is number of ions per molecule in solution (called the van’t Hoff factor), ms is mass of solute in the droplet, and Ms is molecular weight of solute. The two parameters are: c1 = 0.3338 K·µm, and c2 = 4.3x1012 µm3·g–1. Table 7-1 gives properties for common atmospheric solutes.
In eq. (7.11) the relative humidity RH can be greater than 1, corresponding to a relative-humidity percentage (RH% = 100%·es*/es) that is greater than 100%. Similar to eq. (7.3), supersaturation relative to the hydrometeor can be defined as a fraction:
\(\ \begin{align} S=\left(e_{s}^{*} / e_{s}\right)-1\tag{7.12}\end{align}\)
or as a percentage, S% = 100% · S :
\(\ \begin{align} S \%=100 \% \cdot\left[\left(e_{S}^{*} / e_{S}\right)-1\right]\tag{7.13}\end{align}\)
Thus, the left hand side of eq. (7.11) can be easily rewritten as supersaturation.
| Table 7-1. Properties of some solutes. Ms is molecular weight, i is approximate ion count. | |||
| Solute | Chemistry | Ms | i |
|---|---|---|---|
| salt | NaCl | 58.44 | 2 |
| ammonium sulfate | (NH4)2SO4 | 132.13 | 3 |
| hydrogen peroxide | H2O2 | 34.01 | 2 |
| sulfuric acid | H2SO4 | 98.07 | 3 |
| nitric acid | HNO3 | 63.01 | 2 |
Sample Application
Find the equilibrium relative humidity over a droplet of radius 0.2 µm, temperature 20°C, containing 10–16 g of ammonium sulfate.
Find the Answer
Given: R = 0.2 µm, T = 293 K, ms = 10–16 g
Find: RH% = 100%·(es*/es) = ? %
From Table 7-1 for ammonium sulfate:
Ms = 132.13, and i = 3.
Use eq. (7.11):
\(\frac{e_{s}^{*}}{e_{s}} \approx \frac{\exp \left(\frac{0.3338 \mathrm{K} \cdot \mu \mathrm{m}}{(293 \mathrm{K}) \cdot(0.2 \mu \mathrm{m})}\right)}{1+\frac{\left(4.3 \times 10^{12} \mu \mathrm{m}^{3} \cdot \mathrm{g}^{-1}\right) \cdot 3 \cdot\left(10^{-16} \mathrm{g}\right)}{(132.13) \cdot(0.2 \mu \mathrm{m})^{3}}}= 1.00571 / (1+0.00122) = 1.00448\)
RH% = 100%·(es*/es) = 100.448%
Check: Units OK. Physics OK.
Exposition: Fig. 7.7b gives a value of about 100.49% for a temperature of 0°C. Thus, warmer temperatures require less supersaturation of water vapor in the air to prevent the droplet from vaporizing
Sample Application
In fog at 10°C, the vapor pressure is 1.4 kPa. Find the supersaturation fraction and percentage.
Find the Answer
Given: T = 10°C , es* = 1.4 kPa
Find: S = ? , and S% = ?
First, use Table 4-1 in the Water Vapor chapter to find the saturation vapor pressure at 10°C: es = 1.233 kPa. Next, use eq. (7.12):
S = (1.4 kPa / 1.233 kPa) – 1 = 1.135 – 1 = 0.135
S% = 100% · S = 13.5%
Check: es* is indeed > es, thus supersaturated.
Exposition: Unrealistically large, given typical supersaturations in clouds and fog of order S%=1%.
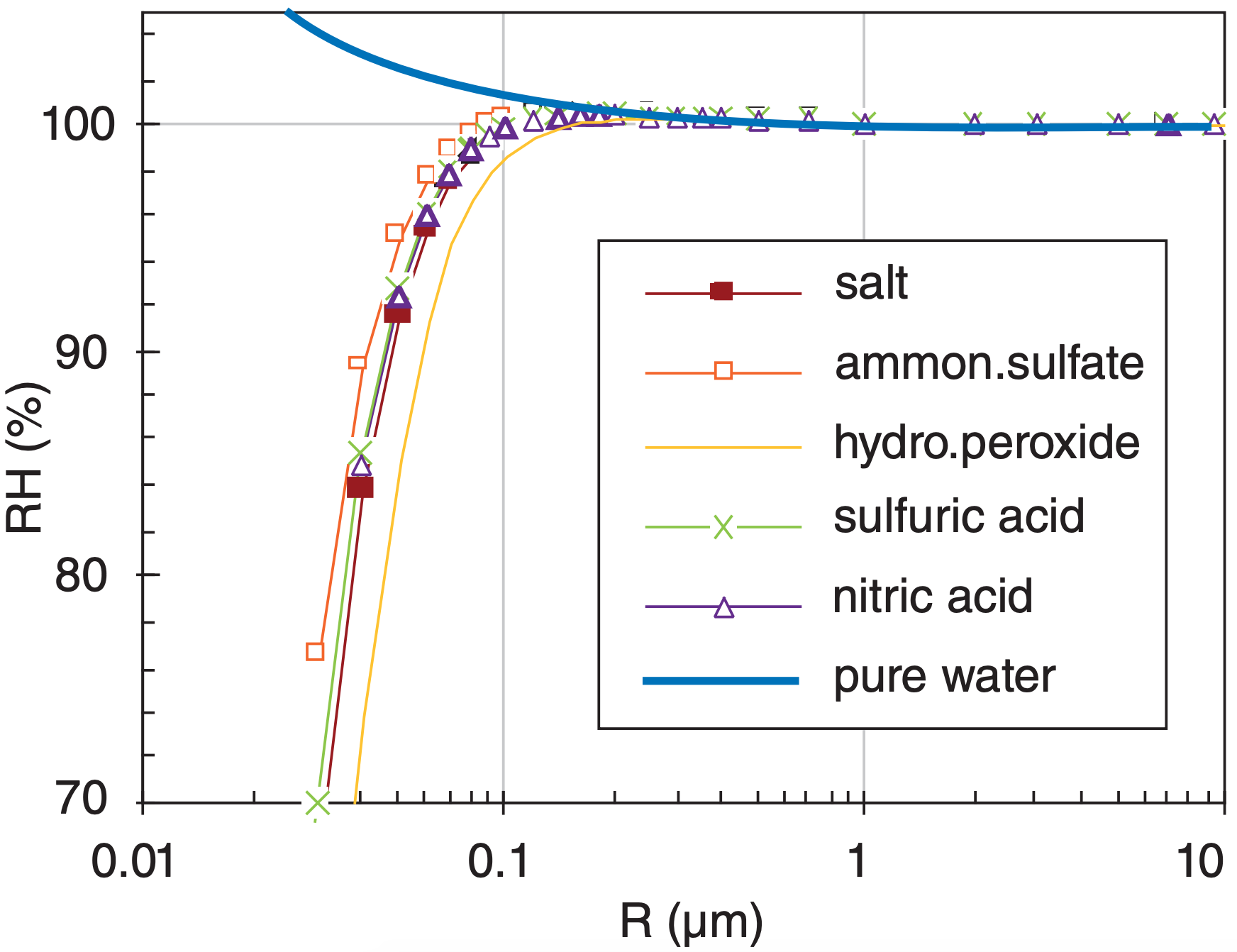
The numerator of eq. (7.11) describes the curvature effect, and together with the left hand side is the Kelvin equation. The denominator describes the solute effect of impurities in the water. Eq. (7.11) was solved in a spreadsheet to produce the Köhler curves in Fig. 7.7. Using these Köhler curves, we can study nucleation.
First, the curve in Fig. 7.7 for pure water increases exponentially as drop radius becomes smaller. This curve was already shown in Fig. 7.6, computed from Kelvin’s equation. It was used to explain why homogeneous nucleation is unlikely, because when the first several water-vapor molecules come together to form a condensate, the droplet radius is so small that the droplet explosively evaporates.
Second, solutions of some chemicals can form small droplets even at humidities of less than 100%. Such hygroscopic (water attracting) pollutants in the air will grow into droplets by taking water vapor out of the air.
Third, if humidities become even slightly greater than the peaks of the Köhler curves, or if droplet radius becomes large enough (see INFO box), then droplets can grow unimpeded. CCN reaching this state are said to be activated. Growth of droplets from activated nuclei continues until enough vapor (i.e., rE) is consumed to reduce the supersaturation back toward 100%. Pure droplets cannot form or co-exist in an environment with neighboring solution droplets, because of the low supersaturation remaining in the air after much of the vapor has condensed out onto the solution droplets. That is another reason why homogeneous nucleation can be neglected for practical purposes.
Fourth, although not shown in these curves, the equations allow droplets to form at lesser supersaturations if the mass of dissolved solute is greater. Hence, larger CCN can grow into droplets earlier and can grow faster than smaller CCN.

To help interpret Fig. 7.7b, consider a droplet containing just one chemical such as salt, in a cloud having a known humidity, such as RH = 100.3%. This is redrawn below.
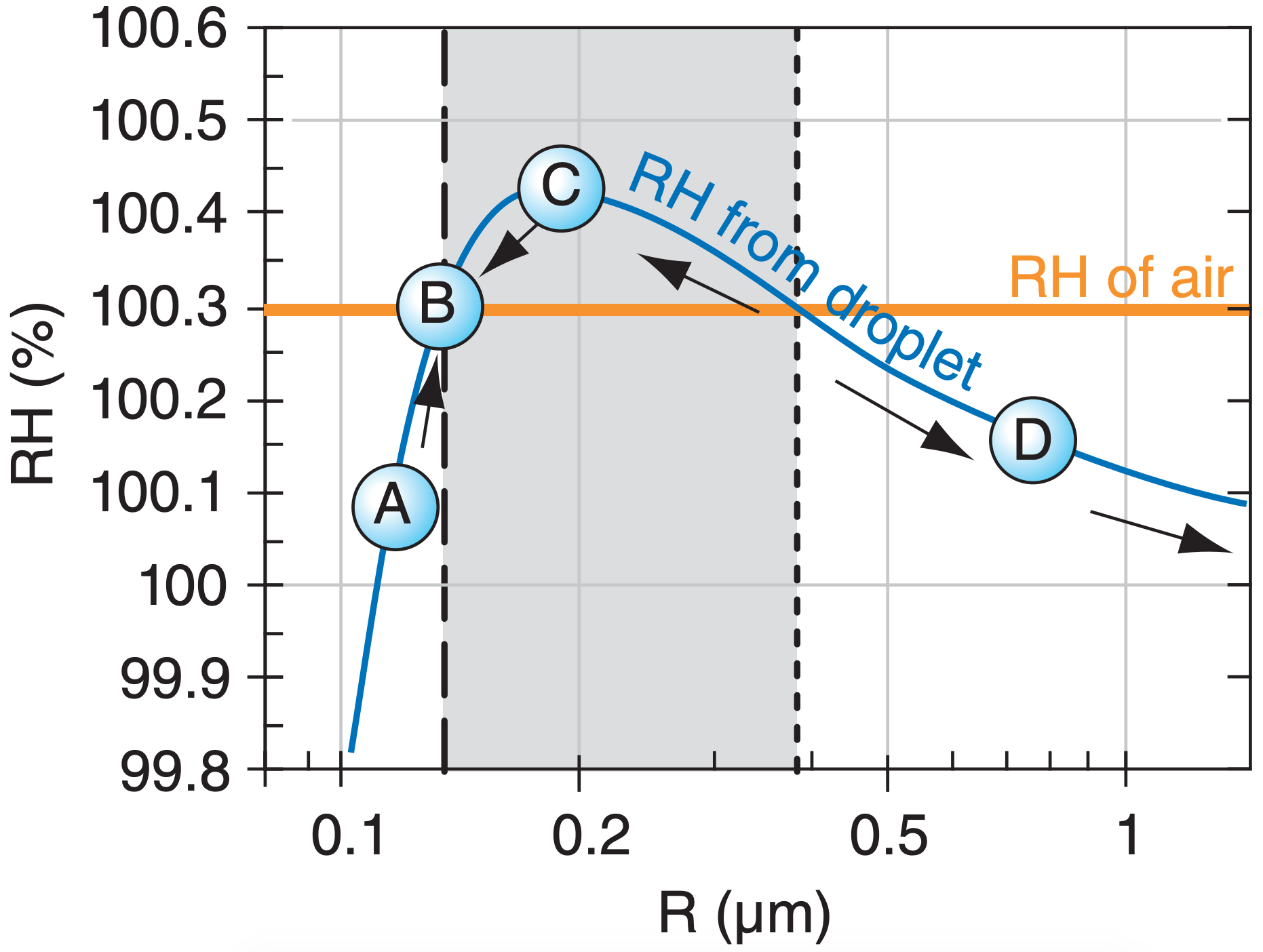
Think of the Köhler curve as the RH associated with the droplet, which is trying to drive evaporation from the droplet. The RH in air (horizontal grey line) is trying to drive condensation to the droplet.
If RHdroplet > RHair, then evaporation > condensation, and the droplet radius becomes smaller as water molecules leave the droplet. This is the situation for any droplet in the light grey band; namely, droplet C suffers net evaporation, causing its radius to decrease toward B.
If RHdroplet < RHair, then evaporation < condensation, and droplet radius increases due to net condensation. Droplet D has this state, and as its radius increases it moves to the right in the graph, causing RHdroplet to decrease further and driving even faster droplet growth. Activated droplets such as these continue growing (shown by right-pointing arrows) until they consume the excess humidity (driving the RHair down toward 100%). Such droplet growth is a first stage in formation of precipitation in warm clouds.
Droplet A also has RHdroplet < RHair, and would tend to increase in radius due to net condensation. But in this part of the Köhler curve, increasing radius causes increasing RHdroplet, and causes the net condensation to diminish until the droplet radius reaches that at B.
Thus, the vertical dotted line in Fig. 7.a is an unstable equilibrium. Namely, a droplet on the Köhler curve at the dotted line would either grow or shrink if perturbed slightly from its equilibrium point.
However, the vertical dashed line is a stable equilibrium point. Droplets approach this radius and then stop growing. Namely, they stay as small haze particles, and do not grow into larger cloud or precipitation particles.
7.2.3. Critical Radius
The location of the peak of the Köhler curves marks the barrier between the larger, activated droplets that can continue to grow, from the smaller haze droplets that reach an equilibrium at small size. The drop radius R* at this peak is called the critical radius, and the corresponding critical supersaturation fraction is S* = es*/es – 1. They are given by:
\(\ \begin{align} R^{*}=\sqrt{\frac{c_{3} \cdot i \cdot m_{s} \cdot T}{M_{s}}}\tag{7.14}\end{align}\)
or
\(\ \begin{align} S^{*}=\sqrt{\frac{c_{4} \cdot M_{s}}{i \cdot m_{s} \cdot T^{3}}}\tag{7.15}\end{align}\)
where c3 = 3.8681x1013 µm2·K–1·g–1, and
c4 = 1.278x10–15 K3·g. For critical supersaturation as a percentage, use S%* = 100%·S*.
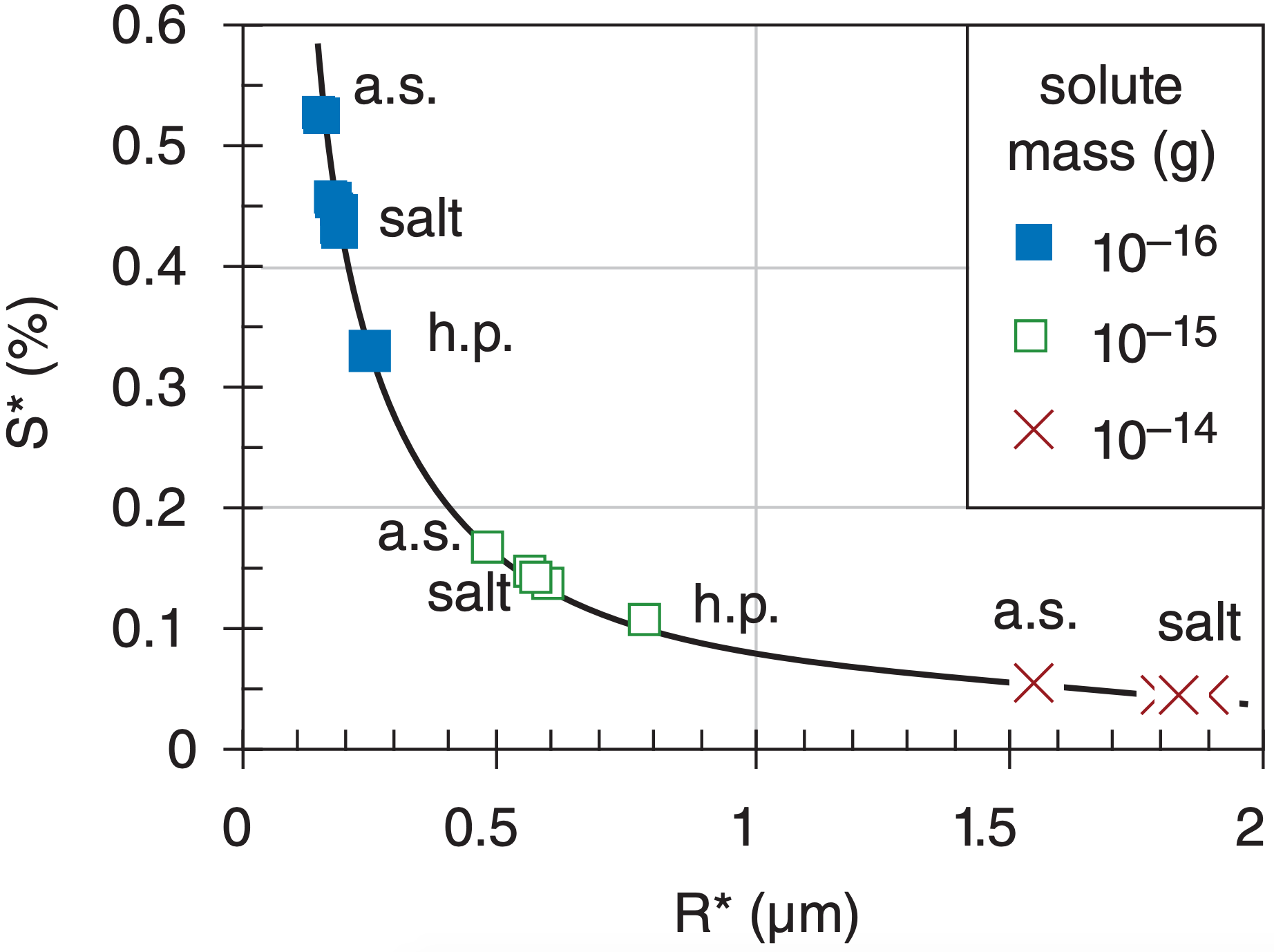
Critical conditions are plotted in Fig. 7.8 for various masses of different chemicals. Obviously S* is inversely related to R*, so as solute mass increases, smaller supersaturations are necessary to reach the critical point, and at that point the droplets will be larger. Also, notice that different chemicals will grow to different sizes, which is one factor causing a range of drop sizes in the cloud.
Sample Application
Find the critical radius and supersaturation value for 10–15 g of ammonium sulfate at 0°C.
Find the Answer
Given: ms = 10–15 g, T = 273 K
Find: R* = ? µm, S%* = ? %.
Use eq. (7.14) & Table 7-1.
\(R^*= \sqrt{\frac{\left(3.8681 \times 10^{13} K^{-1} \cdot g^{-1} \mu m^{2}\right) \cdot 3 \cdot\left(10^{-15} g\right) \cdot(273 K)}{132.13}}\)
R* = 0.49 µm
Use eq. (7.15) & Table 7-1.
\( S^{*}=\sqrt{\frac{\left(1.278 \times 10^{-15} \mathrm{K}^{3} \cdot \mathrm{g}\right) \cdot 132.13}{3 \cdot\left(10^{-15} \mathrm{g}\right) \cdot(273 \mathrm{K})^{3}}}=0.00166\)
S%* = 0.166%
Check: Units OK. Physics OK.
Exposition: Agrees with the point (white square) plotted in Fig. 7.8 for “a.s.”. Thus, the larger mass nucleus needs less supersaturation to become activated.
For a parcel of rising air with increasing supersaturation, the larger nuclei will become activated first, followed by the smaller nuclei if the parcel keeps cooling and if the excess vapor is not removed by the larger nuclei first.
7.2.4. Haze
For conditions left of the peak on any Köhler curve (i.e., R < R*), CCN rapidly grow into small droplets that stop growing at an equilibrium size determined by the humidity, temperature, and solute (see previous INFO box). These small droplets are called haze droplets. Thus, tiny droplets can exist even at relative humidities below 100%.
Haze droplets are aerosols. When a tiny, dry CCN grows to its equilibrium size by the condensation of water molecules, this process is called aerosol swelling. Aerosol swelling is responsible for reducing visibility in polluted air as humidities increase above about 75%.
Even haze particles contain many water molecules. Liquid water contains about ρm = 3.3x1028 molecules m–3. Thus, the smallest haze particles of radius 0.02 µm contain roughly n = ρm·[(4/3)·π·R3] = 1.1 million molecules.
The word smog is a contraction of “smoke” and “fog”, which is a reasonable lay description of haze. Many urban smogs are a stew of ingredients including ozone, volatile hydrocarbons such as evaporated gasoline, and various oxides of nitrogen. These react in the atmosphere, particularly in the presence of sunlight, to create sulfates, nitrates, and hydrogen peroxide CCNs. Aerosol swelling and reduced visibilities are quite likely in such urban smogs, particularly when the air is humid.
Sample Application
For 10–16 g of ammonium sulfate at 0°C, how does haze droplet radius change as RH increases from 70 to 80%? Also, how many molecules are in each aerosol?
Find the Answer
Assume: Same conditions as in Fig. 7.7a.
Given: RH = 70%, 80%.
Find: R = ? µm, n = ? molecules
Solve eq. (7.11), or use Fig. 7.7a. I will use the Fig.
R ≈ 0.027 µm at 70%; R ≈ 0.032 µm at 80%.
The number of molecules is n = ρm·[(4/3)·π·R3]
n = 2.72x106 molecules; n = 4.53x106 molecules
Check: Units OK. Physics OK.
Exposition: Haze particles indeed become larger as relative humidity increases, thereby reducing visibility. Scattering of light by this size of particles is called Mie scattering (see the Atmos. Optics chapter).
Derivation of the critical radius, eq. (7.14).
The critical radius is at es*/es = maximum. But at the maximum, the slope is zero: d(es*/es)/dR = 0. By finding this derivative of eq. (7.11) with respect to R, and setting it to zero, we can solve for R at the maximum. This is R* by definition.
The right side of eq. (7.11) is of the form a/b. A rule of calculus is:
d(a/b)/dR = [b·(da/dR)–a·(db/dR)] / b2.
Also, a is of the form a = exp(f), for which another rule is:
da/dR = a·(df/dR).
Combining these 2 rules and setting the whole thing to zero gives:
\(0=\frac{a}{b}\left[\frac{\mathrm{d} f}{\mathrm{d} R}-\frac{1}{b} \frac{\mathrm{d} b}{\mathrm{d} R}\right]\)
But (a/b) is just the original right side of eq. (7.11), which we know is close to 1.0 at the max, not close to 0. Thus, the eq. above equals 0 only if:
\(\frac{\mathrm{d} f}{\mathrm{d} R}=\frac{1}{b} \frac{\mathrm{d} b}{\mathrm{d} R}\)
Plugging in for f and b and differentiating yields:
\(\frac{-c_{1}}{T \cdot R^{2}}=\frac{1}{\left[1+\frac{c_{2} \cdot i \cdot m_{S}}{M_{s} \cdot R^{3}}\right]} \frac{(-3) \cdot c_{2} \cdot i \cdot m_{s}}{M_{s} \cdot R^{4}}\)
Multiply both sides by (–R4·T/c1) :
\(R^{2}=\left(3 \cdot T / c_{1}\right) \cdot \frac{\left[\frac{c_{2} \cdot i \cdot m_{s}}{M_{s}}\right]}{1+\frac{c_{2} \cdot i \cdot m_{s}}{M_{s} \cdot R^{3}}}\)
Multiply the numerator and denominator of the right side by Ms / (c2·i·ms) , which gives:
\(R^{2}=\left(3 \cdot T / c_{1}\right) \cdot\left[\frac{1}{\left[\frac{M_{s}}{c_{2} \cdot i \cdot m_{s}}+\frac{1}{R^{3}}\right]}\right]\)
By plugging in typical values, we can show that the 1/R3 term is small enough to be negligible compared to the other term in square brackets. This leaves:
\(R^{2} \cong\left(\frac{3 \cdot c_{2}}{c_{1}}\right) \cdot\left(\frac{T \cdot i \cdot m_{S}}{M_{s}}\right)\)
Define c3 = 3·c2 /c1, set R = R*, and take the square root of both sides to get the final answer:
\(\ \begin{align} R^{*} \equiv \sqrt{\frac{c_{3} \cdot i \cdot m_{S} \cdot T}{M_{S}}}\tag{7.14}\end{align}\)
7.2.5. Activated Nuclei
For conditions to the right of the peak on any Köhler curve (i.e., R > R*), CCN are activated and can continue growing. There is no equilibrium that would stop their growth, assuming sufficient water vapor is present. These droplets can become larger than haze droplets, and are called cloud droplets.
Because atmospheric particles consist of a variety of chemicals with a range of masses, we anticipate from the Köhler curves that different CCN will become activated at different amounts of supersaturation. The number density nCCN (# of CCN per m3) activated as a function of supersaturation fraction S is roughly:
\(\ \begin{align} n_{C C N}=c \cdot(100 \cdot S)^{k}\tag{7.16}\end{align}\)
but varies widely. In maritime air, c ≈ 1x108 m–3 and k ≈ 0.7. In continental air c ≈ 6x108 m–3 and k ≈ 0.5. The number of activated nuclei is in the range of 108 to 109 m–3, which is usually just a small fraction of the total number of particles in the air.
The distance x between cloud droplets is on the order of 1 mm, and is given by
\(\ \begin{align} x=n_{C C N}^{-1 / 3}\tag{7.17}\end{align}\)
Sample Application
How many nuclei would be activated in continental air of supersaturation percentage 0.5%? Also, how much air surrounds each droplet, and what is the distance between drops?
Find the Answer
Given: S = 0.005
Find: nCCN = ? particles m–3, Vol = ? mm3, x = ? mm.
(a) Use eq. (7.16):
nCCN = (6x108 m–3)·(0.5)0.5 = 4.24x108 m–3
(b) Also:
Vol = 1/nCCN = 2.36 mm3 droplet–1
(c) Using eq. (7.17): x = Vol1/3 = 1.33 mm.
Check: Units OK. Physics OK.
Exposition: If all of these nuclei become cloud droplets, then there are over 40 million droplets within each cubic meter of cloud. But there is a relatively large distance between each drop.


