4.0: Vapor Pressure at Saturation
- Page ID
- 9547
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Total atmospheric pressure is the sum of the partial pressures of all the constituents. For water vapor, the partial pressure is called the vapor pressure, e. Vapor pressure has units of kPa.
Gases in the air can mix with any relative proportions. However, for water vapor, there is a critical water-vapor concentration, known as the saturation humidity. Above this critical value, water vapor condenses faster than it evaporates, thereby reducing the water-vapor concentration back to the critical value. At this critical value, the air is said to be saturated, and the vapor is in equilibrium with liquid water. Let es represent the saturation vapor pressure at equilibrium over pure water having a flat surface.
It frequently happens that air holds less than the critical value, and is said to be unsaturated. For this case, e < es.
Although any portion of water vapor can be held in air, it is rare for the vapor pressure to be more than 1% greater than the saturation value. Air having e > es is said to be supersaturated. Supersaturated air can occur as a transient condition while excess water vapor is condensing onto available surfaces such as on dust particles called cloud condensation nuclei. However, photographs of air flow over aircraft wings for both subsonic and supersonic flight through humid air indicate that condensation to form cloud droplets occurs almost instantly.
During the equilibrium state (i.e., at saturation) there is a balance between the rate of evaporation from the liquid and the rate of condensation from vapor. Liquid-water temperature controls the rate of evaporation, and humidity (water-vapor concentration in air) controls the rate of condensation.

Warmer liquid temperatures cause greater evaporation rates, which allow the humidity in the air to increase until a new balance is attained. The opposite is true for colder temperatures. For a situation where the air and liquid water temperatures are equal, we conclude that colder air has a smaller capacity for holding water vapor than warmer air.
This relationship between saturation vapor pressure and temperature is approximated by the Clausius-Clapeyron equation:
\(\ \begin{align} e_{s} \approx e_{o} \cdot \exp \left[\dfrac{L}{\Re_{v}} \cdot\left(\dfrac{1}{T_{o}}-\dfrac{1}{T}\right)\right]\tag{4.1a}\end{align}\)
where the water-vapor gas constant is ℜv = 461 J·K–1·kg–1, To = 273.15 K, eo = 0.6113 kPa, and L is a latent-heat parameter. Temperatures in this equation must have units of Kelvin.
This equation works for saturation over both liquid water and solid water (ice) surface if these surfaces are flat. For liquid water the latent heat of vaporization L = Lv = 2.5x106 J·kg–1, giving Lv/ℜv = 5423 K. For ice the latent heat of deposition L = Ld = 2.83x106 J·kg–1 and Ld/ℜv = 6139 K.
The exponentially-shaped curve described by eq. (4.1a) is plotted in Figure 4.1, with corresponding data values listed Table 4-1. One interpretation of this curve is that as unsaturated humid air is cooled, a temperature is reached at which point the air is saturated. Further cooling forces some water vapor to condense into liquid, creating clouds and rain and releasing latent heat. Hence, the Clausius-Clapeyron equation is important for understanding storms.
Sample Application
Air of temperature 30°C has what value of es?
Find the Answer
Given: T = 30°C = 303.15 K
Find: es = ? kPa for over liq. water. Apply eq. (4.1a).
\(\begin{aligned} e_{s} &=(0.6113 \mathrm{kPa}) \cdot \exp \left[(5423 \mathrm{K}) \cdot\left(\dfrac{1}{273.15 \mathrm{K}}-\dfrac{1}{303.15 \mathrm{K}}\right)\right] \\ &=(0.6113 \mathrm{kPa}) \cdot \exp (1.96473)=4.36 \mathrm{kPa} \end{aligned}\)
Check: Physics reasonable, & agrees with Table 4-1.
Exposition: At saturation for this T, water-vapor partial pressure is only 4.3% of total pressure P≈101.3 kPa.
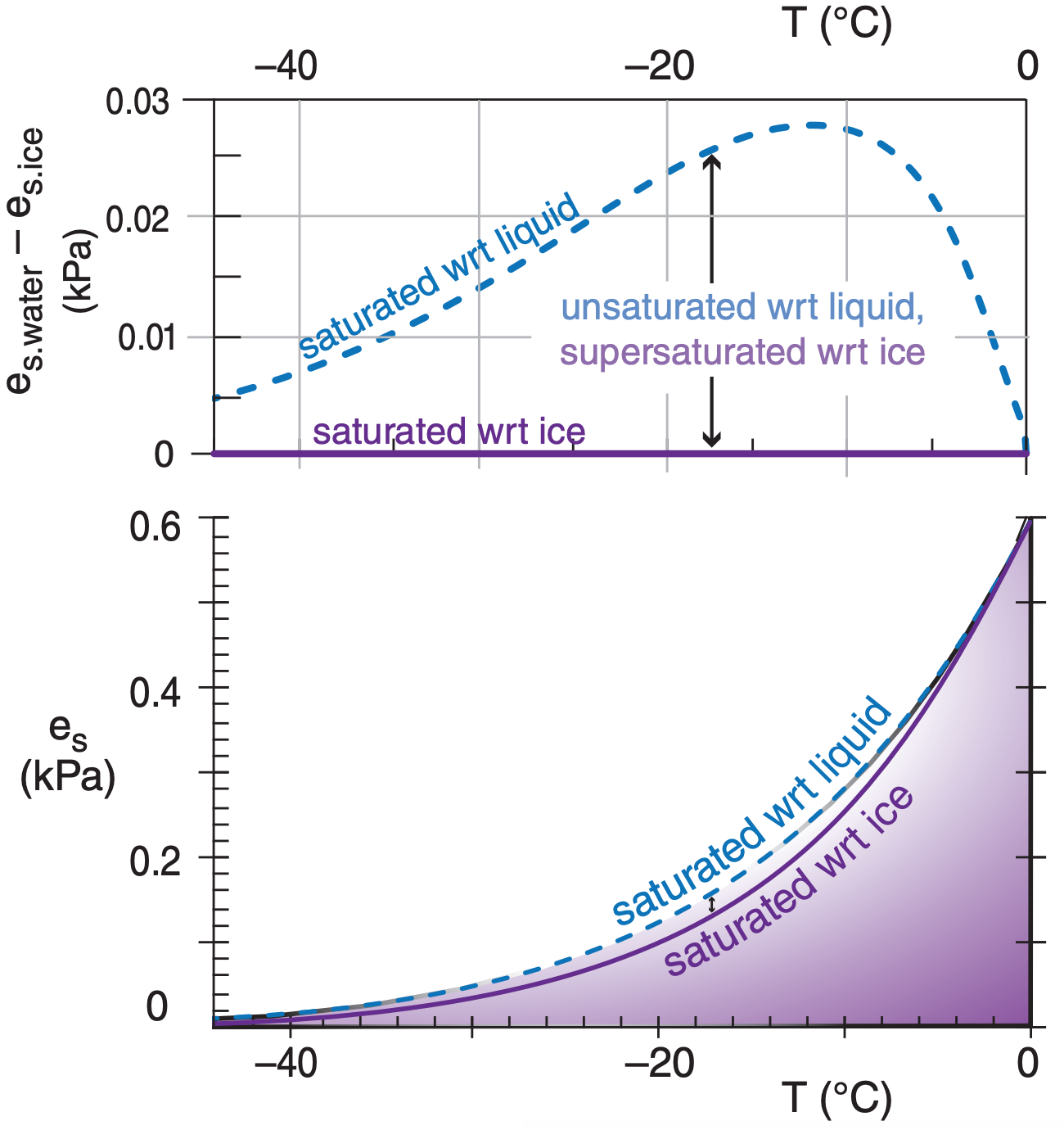
In the atmosphere it is possible for liquid water to remain unfrozen at temperatures down to –40°C. Such unfrozen cold water is said to be supercooled. The difference between saturation values of water vapor over supercooled liquid water and ice is plotted in Figure 4.2.
The Clausius-Clapeyron equation also describes the relationship between actual (unsaturated) water-vapor pressure e and dew-point temperature (Td, to be defined later):
\(\ \begin{align}e=e_{o} \cdot \exp \left[\dfrac{L}{\Re_{v}} \cdot\left(\dfrac{1}{T_{o}}-\dfrac{1}{T_{d}}\right)\right]\tag{4.1b}\end{align}\)
where To = 273.15 K and eo = 0.6113 kPa as before. Use, L/ℜv = Lv/ℜv = 5423 K for liquid water, and use Ld/ℜv = 6139 K for ice.
The latent-heat parameter L varies slightly with temperature. Taking that into account, a different approximation known as Tetens’ formula has been suggested for saturation vapor pressure es as a function of temperature (T, in Kelvins):
\(\ \begin{align}e_{s}=e_{o} \cdot \exp \left[\dfrac{b \cdot\left(T-T_{1}\right)}{T-T_{2}}\right]\tag{4.2}\end{align}\)
where b = 17.2694, eo = 0.6113 kPa, T1 = 273.15 K, and T2 = 35.86 K.
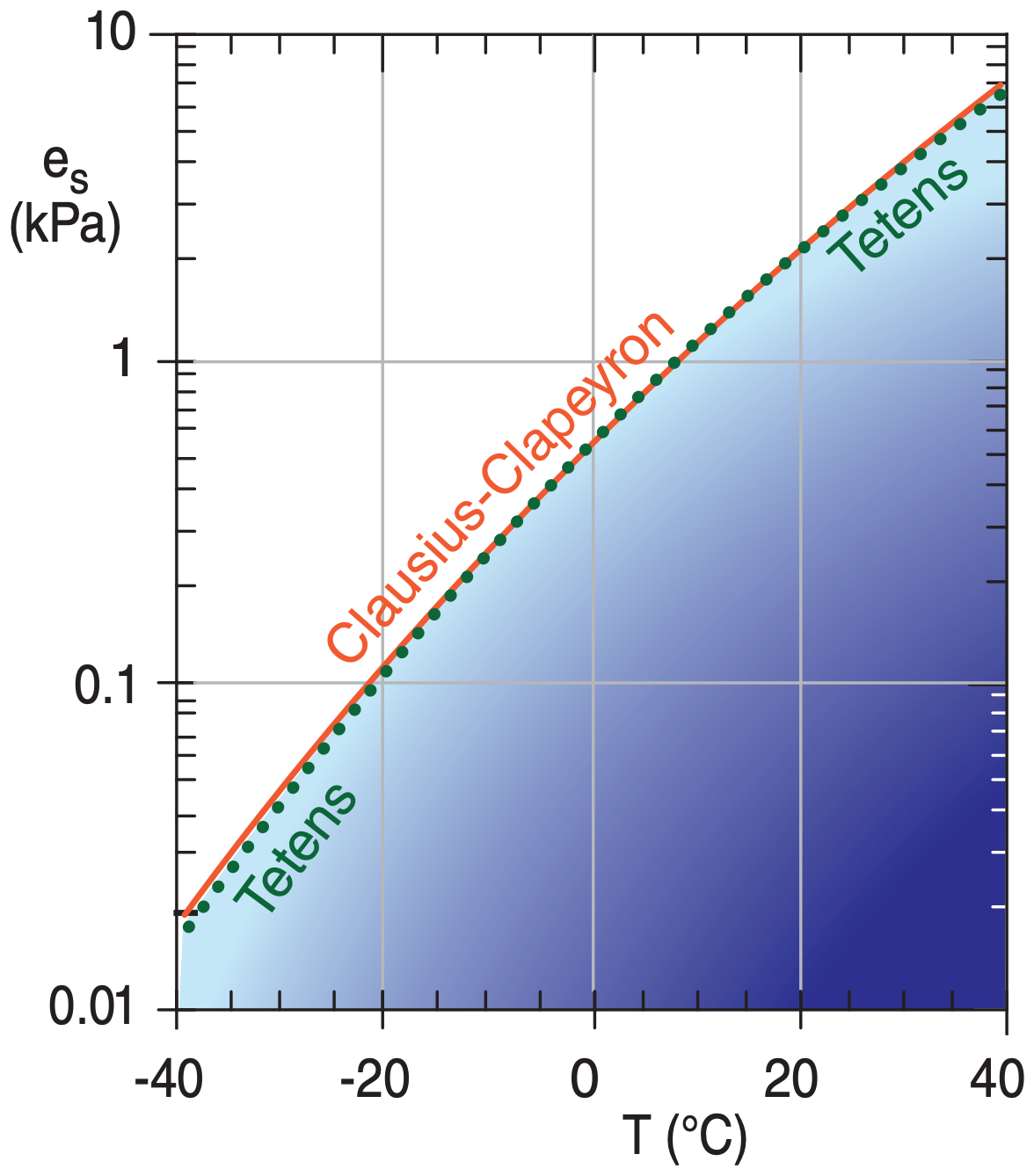
Sample Application
How do the vapor pressure values from Tetens’ formula differ from those of the Clausius-Clapeyron equation, as a function of temperature?
Find the Answer
Use a spreadsheet to solve eqs. (4.1a) and (4.2) .
Check: Physics and units are reasonable.
Exposition: The difference between both formulas are very small — often smaller than other uncertainties in measurements of temperature or humidity. So you can be confident using either equation
Rudolf Clausius and Benoît Paul Émilie Clapeyron were engineers trying to improve steam engines during the 1800’s. They independently made laboratory measurements of water vapor pressure at saturation es, and found the following empirical relationship:
\(\dfrac{d e_{s}}{d T}=\dfrac{L_{v}}{T}\left[\dfrac{1}{\rho_{v}}-\dfrac{1}{\rho_{L}}\right]^{-1}\)
where ρL is liquid-water density, and ρv is water-vapor density (i.e., absolute humidity). The liquidwater density is so much greater than the water-vapor density that the above equation can be approximated by:
\(\dfrac{d e_{s}}{d T} \cong \dfrac{L_{v}}{T} \rho_{v}\)
The relationship between saturation vapor pressure and the absolute humidity is given by the ideal gas law for water vapor:
\(e_{S}=\rho_{v} \cdot \Re_{v} \cdot T\)
where the water-vapor gas constant is ℜv = 4.615x10–4 kPa K–1 (g m–3)–1. You can solve the ideal gas law for ρv , which you can then use in the previous eq:
\(\dfrac{d e_{s}}{d T} \cong \dfrac{L_{v} \cdot e_{s}}{\Re_{v} \cdot T^{2}}\)
This equation admits a solution if you separate the variables to put all terms involving T on the right, and all those involving es on the left:
\(\dfrac{d e_{s}}{e_{s}} \cong \dfrac{L_{v}}{\mathfrak{R}_{v}} \dfrac{d T}{T^{2}}\)
Next, integrate between some known condition (eo at To) to any arbitrary values of saturation vapor pressure (es) and temperature (T):
\(\int_{e_{0}}^{e_{\mathrm{s}}} \dfrac{d e_{s}}{e_{s}} \cong \dfrac{L_{v}}{\mathfrak{R}_{v}} \int_{T_{o}}^{T} \dfrac{d T}{T^{2}}\)
After integrating you get:
\(\ln \left(\dfrac{e_{S}}{e_{o}}\right) \cong-\dfrac{L_{v}}{\Re_{v}}\left[\dfrac{1}{T}-\dfrac{1}{T_{o}}\right]\)
To get eq. (4.1a) take the exponential (i.e., antilog) of both sides and then algebraically rearrange to give:
\(\ \begin{align} e_{s}=e_{o} \cdot \exp \left[\dfrac{L}{\Re_{v}} \cdot\left(\dfrac{1}{T_{o}}-\dfrac{1}{T}\right)\right]\tag{4.1}\end{align}\)
Details are given in the Atmospheric Thermodynamics book by C. Bohren and B. Albrecht (1998, Oxford Univ. Press, 402 pp).
Liquids boil when the saturation vapor pressure es equals the ambient pressure P of the atmosphere:
\(P=e_{s}\)
Variation of boiling temperature with Altitude
We know es as a function of temperature T from the Clausius-Clapeyon equation, so plug that into the right side of the equation above. We also know that ambient atmospheric pressure P decreases exponentially with increasing height z, as was given in Chapter 1, so we can plug that into the left side. This gives
\(P_{o} \cdot \exp \left[-\dfrac{z}{H_{p}}\right]=e_{o} \cdot \exp \left[\dfrac{L_{v}}{\Re_{v}} \cdot\left(\dfrac{1}{T_{o}}-\dfrac{1}{T}\right)\right]\)
where Po = 101.325 kPa, Hp ≈ 7.29 km, eo = 0.6113 kPa, Lv /ℜv = 5423 K, and To = 273.15 K.
Next, divide the left and right sides of the equation by Po. On the right side, note that eo/Po = exp[ln(eo/ Po)]. Thus:
\(\exp \left[-\dfrac{z}{H_{p}}\right]=\exp \left[\ln \left(\dfrac{e_{o}}{P_{o}}\right)+\dfrac{L_{v}}{\Re_{v}}\left(\dfrac{1}{T_{o}}\right)-\dfrac{L_{v}}{\Re_{v}} \dfrac{1}{T}\right]\)
Create a new constant called a (dimensionless) that is the sum of the first two terms inside the square brackets, because those two terms are constant. Next, take the ln of the right and left sides to give:
\(\dfrac{z}{H_{p}}=\dfrac{L_{v}}{\Re_{v}} \dfrac{1}{T}-a\)
Solve this equation for T, which we can re-define as the boiling point Tboiling:
\(T_{\text {boiling }}=\dfrac{L_{v} / \Re_{v}}{a+z / H_{p}}\)
Knowing that at sea level (z = 0) the boiling temperature is 100°C (i.e., Tboiling = 373.15 K) you can solve for the dimensionless constant, giving : a = 14.53.
Exposition:
If you solve this equation for various altitudes, you find that the boiling point decreases by 3.4°C km–1. Thus, Tboiling = 366.35 K = 93.2°C at 2 km altitude
To soften vegetables to the desired tenderness or to prepare meats to the desired doneness, foods must be cooked at a certain temperature over a certain time duration. Slightly cooler cooking temperatures must be compensated with slightly longer cooking times. Thus, you need to cook boiled foods for longer times at higher altitudes, because boiling happens at a lower temperature.
Table 4-1. Values of humidity variables at saturation (subscript s) over a liquid-water flat surface, for different air temperatures T. The same values also relate the dew-point temperature Td to the actual humidity. Notation: e = vapor pressure, r = mixing ratio, q = specific humidity, ρv = absolute humidity. Note that r and q depend on pressure — this table shows their values for standard sea-level pressure.
| For P = 101.325 kPa | ||||
| T | es | qs | rs | ρvs |
| or | ||||
| Td | e | q | r | ρv |
| (°C) | (kPa) | (g kg–1) | (g kg–1) | (g m–3) |
|
–40 –35 –30 –25 –20 –15 –10 –5 0 5 10 15 20 25 30 35 40 45 50 55 60 |
0.0203 0.0330 0.0528 0.0827 0.1274 0.1929 0.2875 0.4222 0.6113 0.8735 1.232 1.718 2.369 3.230 4.360 5.829 7.720 10.13 13.19 17.04 21.83 |
0.1245 0.2029 0.324 0.5079 0.7822 1.1848 1.7666 2.5956 3.7611 5.3795 7.6005 10.62 14.67 20.07 27.21 36.58 48.8 64.66 85.18 111.7 145.9 |
0.1245 0.2029 0.3241 0.5082 0.7828 1.1862 1.7697 2.6024 3.7753 5.4086 7.6587 10.73 14.89 20.48 27.97 37.97 51.3 69.13 93.11 125.7 170.8 |
0.1886 0.301 0.4708 0.7231 1.0914 1.6206 2.3697 3.4151 4.8546 6.8119 9.4417 12.94 17.53 23.5 31.2 41.03 53.48 69.1 88.56 112.6 142.2 |


