1.5: Earth Frameworks Reviewed
- Page ID
- 9528
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Earth is slightly flattened into an oblate spheroid of revolution (Figure 1.5). The distance from the center of the Earth to the north (N) and south (S) poles is roughly 6356.755 km, slightly less than the 6378.140 km distance from the center to the equator. This 21 km difference in Earth radius causes a north-south cross section (i.e., a slice) of the Earth to be slightly elliptical. But for all practical purposes you can approximate the Earth a sphere (except for understanding Coriolis force in the Forces & Winds chapter).
Sample Application
A thunderstorm top is at azimuth 225° and elevation angle 60° from your position. How would you describe its location in words? Also, what is the zenith angle?
Find the Answer:
Given: α = 225° Ψ = 60°.
Find: Location in words, and find ζ .
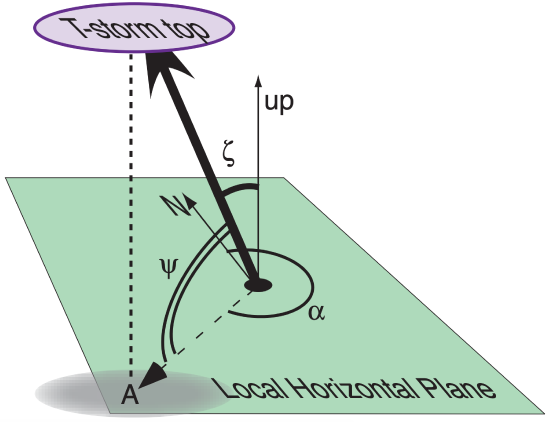
Sketch: (see above)
Because south has azimuth 180°, and west has azimuth 270°, we find that 225° is exactly halfway between south and west. Hence, the object is southwest (SW) of the observer. Also, 60° elevation is fairly high in the sky. So the thunderstorm top is high in the sky to the southwest of the observer.
Rearrange equation [ Ψ = 90° – ζ ] to solve for zenith angle: ζ = 90° – ψ = 90° - 60° = 30°.
Check: Units OK. Locations reasonable. Sketch good.
Exposition: This is a bad location for a storm chaser (the observer), because thunderstorms in North America often move from the SW toward the northeast (NE). Hence, the observer should quickly seek shelter underground, or move to a different location out of the storm path.
Table 1-1. Time zones in North America. ST = standard time in the local time zone. DT = daylight time in the local time zone. UTC = coordinated universal time. For conversion, use:
ST = UTC – α , DT = UTC – β
| Zone | Name | α (h) | β (h) |
|---|---|---|---|
| P* | Newfoundland | 3.5 (NST) | 2.5 (NDT) |
| Q | Atlantic | 4 (AST) | 3 (ADT) |
| R | Eastern | 5 (EST) | 4 (EDT) |
| S | Central, and Mexico | 6 (CST) 6 (MEX) |
5 (CDT) 5 |
| T | Mountain | 7 (MST) | 6 (MDT) |
| U | Pacific | 8 (PST) | 7 (PDT) |
| V | Alaska | 9 (AKST) | 8 (AKDT) |
| W | Hawaii-Aleutian | 10 (HST) | 9 (HDT) |
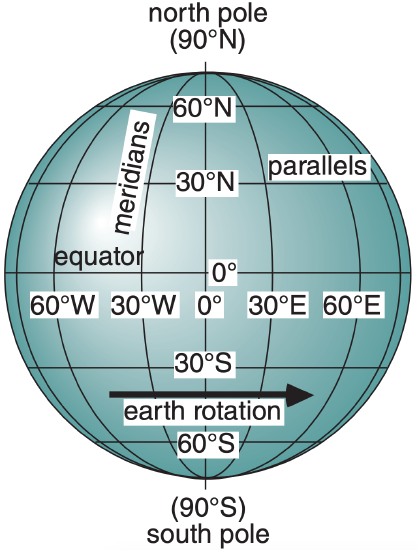
1.3.1. Cartography
Recall that north-south lines are called meridians, and are numbered in degrees longitude. The prime meridian (0° longitude) is defined by international convention to pass through Greenwich, Great Britain. Longitude is positive east of the prime meridian, and negative west. We often divide the 360° of longitude around the Earth into halves relative to Greenwich:
- Western Hemisphere: 0 – 180°W,
- Eastern Hemisphere: 0 – 180°E.
Looking toward the Earth from above the north pole, the Earth rotates counterclockwise about its axis. This means that all objects on the surface of the Earth (except at the poles) move toward the east. East-west lines are called parallels, and are numbered in degrees latitude. By convention, the equator is defined as 0° latitude; the north pole is at 90°N; and the south pole is at 90°S. Latitude is positive north of the equator, and negative south. Between the north and south poles are 180° of latitude, although we usually divide the globe into the:
- Northern Hemisphere: 0 – 90°N,
- Southern hemisphere: 0 – 90°S.
On the surface of the Earth, each degree of latitude equals 111 km, or 60 nautical miles.
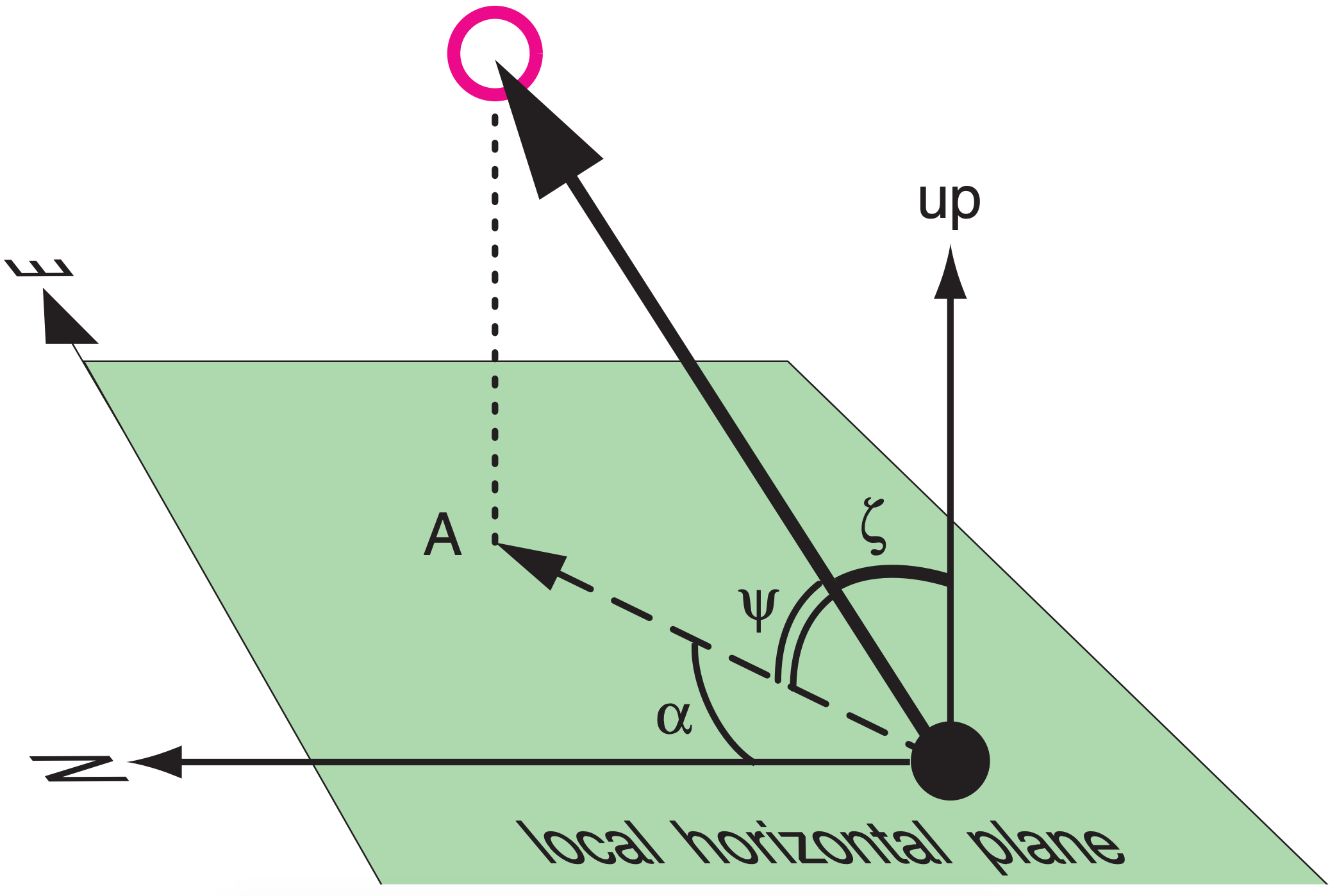
1.3.2. Azimuth, Zenith, & Elevation Angles
As a meteorological observer on the ground (black circle in Figure 1.6), you can describe the local angle to an object (white circle) by two angles: the azimuth angle (α), and either the zenith angle (ζ) or elevation angle (ψ). The object can be physical (e.g., sun, cloud) or an image (e.g., rainbow, sun dog). By “local angle”, we mean angles measured relative to the Cartesian local horizontal plane (e.g., a lake surface, or flat level land surface such as a polder), or relative to the local vertical direction at your location. Local vertical (up) is defined as opposite to the direction that objects fall.
Zenith means “directly overhead”. Zenith angle is the angle measured at your position, between a conceptual line drawn to the zenith (up) and a line drawn to the object (dark arrow in Figure 1.6). The elevation angle is how far above the horizon you see the object. Elevation angle and zenith angle are related by: ψ = 90° – ζ , or if your calculator uses radians, it is ψ = π/2 – ζ. Abbreviate both of these forms by ψ = C/4 – ζ, where C = 360° = 2π radians.
For the azimuth angle, first project the object vertically onto the ground (A, in Figure 1.6). Draw a conceptual arrow (dashed) from you to A; this is the projection of the dark arrow on to the local horizontal plane. Azimuth angle is the compass angle along the local horizontal plane at your location, measured clockwise from the direction to north (N) to the direction to A.
1.3.3. Time Zones
In the old days each town defined their own local time. Local noon was when the sun was highest in the sky. In the 1800s when trains and telegraphs allowed fast travel and communication between towns, the railroad companies created standard time zones to allow them to publish and maintain precise schedules. Time zones were eventually adopted worldwide by international convention. The Earth makes one complete revolution (relative to the sun) in one day. One revolution contains 360° of longitude, and one day takes 24 hours, thus every hour of elapsed time spans 360°/24 = 15° of longitude. For this reason, each time zone was created to span 15° of longitude, and almost every zone is 1 hour different from its neighboring time zones. Everywhere within a time zone, all clocks are set to the same time. Sometimes the time-zone boundaries are modified to follow political or geographic boundaries, to enhance commerce.
Coordinated Universal Time (UTC) is the time zone at the prime meridian. It is also known as Greenwich Mean Time (GMT) and Zulu time ( Z ). The prime meridian is in the middle of the UTC time zone; namely, the zone spreads 7.5° on each side of the prime meridian. UTC is the official time used in meteorology, to help coordinate simultaneous weather observations around the world.
Internationally, time zones are given letter designations A - Z, with Z at Greenwich, as already discussed. East of the UTC zone, the local time zones (A, B, C, ...) are ahead; namely, local time of day is later than at Greenwich. West of the UTC zone, the local time zones (N, O, P, ...) are behind; namely, local time of day is earlier than at Greenwich.
Each zone might have more than one local name, depending on the countries it spans. Most of western Europe is in the Alpha (A) zone, where A = UTC + 1 hr. This zone is also known as Central Europe Time (CET) or Middle European Time (MET). In N. America are 8 time zones P* - W (see Table 1-1).
Near 180° longitude (in the middle of the Pacific Ocean) is the international date line. When you fly from east to west across the date line, you lose a day (it becomes tomorrow). From west to east, you gain a day (it becomes yesterday).
Many countries utilize Daylight Saving Time (DT) during their local summer. The purpose is to shift one of the early morning hours of daylight (when people are usually asleep) to the evening (when people are awake and can better utilize the extra daylight). At the start of DT (often in March in North America), you set your clocks one hour ahead. When DT ends in Fall (November), you set your clocks one hour back. The mnemonic “Spring ahead, Fall back” is a useful way to remember.
Times can be written as two or four digits. If two, then these digits are hours (e.g., 10 = 10 am, and 14 = 2 pm). If four, then the first two are hours, and the last two are minutes (e.g., 1000 is 10:00 am, and 1435 is 2:35 pm). In both cases, the hours use a 24-h clock going from 0000 (midnight) to 2359 (11:59 pm).
Sample Application
A weather map is valid at 12 UTC on 5 June. What is the valid local time in Reno, Nevada USA? Hint: Reno is at roughly 120°W longitude.
Find the Answer
Given: UTC = 12 , Longitude = –120° = 120°W.
Find: Local valid time.
First, determine if standard or daylight time: Reno is in the N. Hem., and 5 June is after the start date (March) of DT, so it is daylight time.
Hint: each 15° longitude = 1 time zone.
Next, use longitude to determine the time zone. –120° / (15° / zone) = –8 zones.
But –8 zones difference corresponds to the Pacific Time Zone. (using the ST column of Table 1-1, for which α also indicates the difference in time zones from UTC)
Use Table 1-1 for Pacific Daylight Time: β = 7 h PDT = UTC – 7 h = 12 – 7 = 5 am PDT.
Check: Units OK. 5 am is earlier than noon.
Exposition: In the USA, Canada, and Mexico, 12 UTC maps always correspond to morning of the same day, and 00 UTC maps correspond to late afternoon or evening of the previous day.
Caution: The trick of dividing the longitude by 15° doesn’t work for some towns, where the time zone has been modified to follow geo-political boundaries.
Fast-moving air molecules that don’t hit other molecules can escape to space by trading their kinetic energy (speed) for potential energy (height). High in the atmosphere where the air is thin, there are few molecules to hit. The lowest escape altitude for Earth is about 550 km above ground, which marks the base of the exosphere (region of escaping gases). This equals 6920 km when measured from the Earth’s center, and is called the critical radius, rc.
The escape velocity, ve , is given by
\(\
v_e = [\frac{2\cdot G \cdot m_{planet}}{r_c}]^{1/2}
\)
where G = 6.67x10–11 m3·s–2·kg–1 is the gravitational constant, and mplanet is the mass of the planet. The mass of the Earth is 5.975 x 1024 kg. Thus, the escape velocity from Earth is roughly ve = 10,732 m s–1.
Using this velocity in eq. (1.5) gives the temperature needed for average-speed molecules to escape: 9,222 K for H2, and 18,445 K for the heavier He. Temperatures in the exosphere (upper thermosphere) are not hot enough for average-speed H2 and He to escape, but some are faster than average and do escape.
Heavier molecules such as O2 have unreachably high escape temperatures (147,562 K), and have stayed in the Earth’s atmosphere, to the benefit of life.


