11.11: Extratropical Ridges and Troughs (Rossby Waves)
- Page ID
- 10211
The atmosphere is generally warm near the equator and cool near the poles. This meridional temperature gradient drives a west-to-east wind having increasing speed with increasing altitude within the troposphere, as described by the thermal-wind effect. The resulting fast wind near the tropopause is called the jet stream. To first order, we would expect this jet stream to encircle the globe (Fig. 11.49a) along the zone between the warm and cool airmasses, at roughly 50 to 60° latitude in winter.
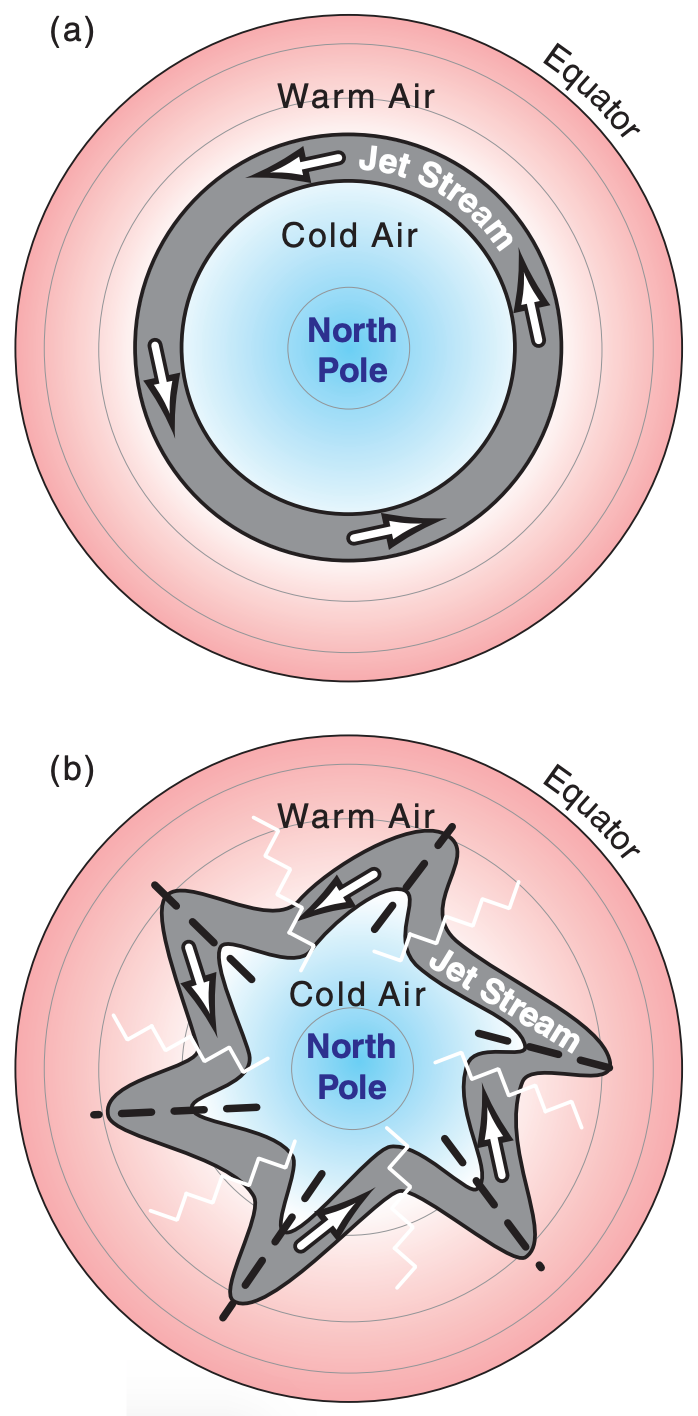
However, this flow is unstable, allowing small disturbances (e.g., flow over mountain ranges) to grow into large north-south meanders (Fig. 11.49b) of the jet stream. These meanders are called Rossby waves or planetary waves. Typical wavelengths are 3 - 4 Mm. Given the circumference of a parallel at those latitudes, one typically finds 3 to 13 waves around the globe, with a normal zonal wavenumber of 7 to 8 waves.
The equatorward region of any meander is called a trough (pronounced like “troff”) and is associated with low pressure or low geopotential height. The poleward portion of a meander is called a ridge, and has high pressure or height. The turning of winds around troughs and ridges are analogous to the turning around closed lows and highs, respectively. The trough center or trough axis is labeled with a dashed line, while the ridge axis is labeled with a zig-zag symbol (Fig. 11.49b).
Like many waves or oscillations in nature, Rossby waves result from the interplay between inertia (trying to make the jet stream continue in the direction it was deflected) and a restoring force (acting opposite to the deflection). For Rossby waves, the restoring force can be explained by the conservation of potential vorticity, which depends on both the Coriolis parameter and the layer thickness (related to layer static stability). Baroclinic instability considers both restoring factors, while barotropic instability is a simpler approximation that considers only the Coriolis effect.
11.11.1. Barotropic Instability
Consider tropospheric air of constant depth ∆z (≈ 11 km). For this situation, the conservation of potential vorticity can be written as
\( \begin{align} \left[\frac{M}{R}+f_{c}\right]_{\text {initial}}=\left[\frac{M}{R}+f_{c}\right]_{\text {later}}\tag{11.34}\end{align}\)
where jet-stream wind speed M divided by radius of curvature R gives the relative vorticity, and fc is the Coriolis parameter (which is a function of latitude).

(Location a in Fig. 11.50) Consider a jet stream at initial latitude Yo moving in a straight line from the southwest. At that latitude it has a certain value of the Coriolis parameter, but no relative vorticity (M/R = 0, because R = ∞ for a straight line). But fc increases as the air moves poleward, thus the M/R term on the right side of eq. (11.34) must become smaller than its initial value (i.e., it becomes negative) so that the sum on the right side still equals the initial value on the left side.
(Location b) We interpret negative curvature as anticyclonic (clockwise turning in the N. Hemisphere). This points the jet stream equatorward.
(Location c) As the air approaches its starting latitude, its Coriolis parameter decreases toward its starting value. This allows the flow to become a straight line again at location c. But now the wind is blowing from the northwest, not the southwest.
(Location d) As the air overshoots equatorward, fc gets smaller, requiring a positive M/R (cyclonic curvature) to maintain constant potential vorticity. This turns the jet stream back toward its starting latitude, where the cycle repeats. The flow is said to be barotropically unstable, because even pure, non-meandering zonal flow, if perturbed just a little bit from its starting latitude, will respond by meandering north and south.
This north-south (meridional) oscillation of the west-to-east jet stream creates the wavy flow pattern we call a Rossby wave or a planetary wave. Because the restoring force was related to the change of Coriolis parameter with latitude, it is useful to define a beta parameter as
\(\ \begin{align} \beta=\frac{\Delta f_{C}}{\Delta y}=\frac{2 \cdot \Omega}{R_{\text {earth }}} \cdot \cos \phi\tag{11.35}\end{align}\)
where the average radius of the Earth is REarth =6371 km. For 2·Ω/REarth = 2.29x10–11 m–1·s–1, one finds that β is roughly (1.5 to 2)x10–11 m–1·s–1.
The wave path in Fig. 11.50 can be approximated with a simple cosine function:
\(\ \begin{align} y^{\prime} \approx A \cdot \cos \left[2 \pi \cdot\left(\frac{x^{\prime}-c \cdot t}{\lambda}\right)\right]\tag{11.36}\end{align}\)
where the displacement distance of the Rossby wave from Yo (its starting latitude) is y’ . Let x’ be the eastward distance from the start of the wave. The position of the wave crests move at phase speed c with respect to the Earth. The wavelength is λ and its amplitude is A (see Fig. 11.50). The primes indicate the deviations from a mean background state.
Barotropic Rossby waves of the jet stream have wavelengths of about λ ≈ 6000 km and amplitudes of about A ≈ 1665 km, although a wide range of both is possible. Typically 4 to 5 of these waves can fit around the earth at mid-latitudes (where the circumference of a latitude circle is 2π·REarth·cosϕ , and ϕ is latitude).
The waves move through the air at intrinsic phase speed co :
\(\ \begin{align} c_{o}=-\beta \cdot\left(\frac{\lambda}{2 \pi}\right)^{2}\tag{11.37}\end{align}\)
The negative sign means that the wave crests propagate toward the west relative to the air.
However, the air in which the wave is embedded is itself moving toward the east at wind speed Uo. Thus, relative to the ground, the phase speed c is:
\(\ \begin{align} c=U_{o}+c_{o}\tag{11.37b}\end{align}\)
Given typical values for Uo, the total phase speed c relative to the ground is positive. Such movement toward the east is indeed observed on weather maps.
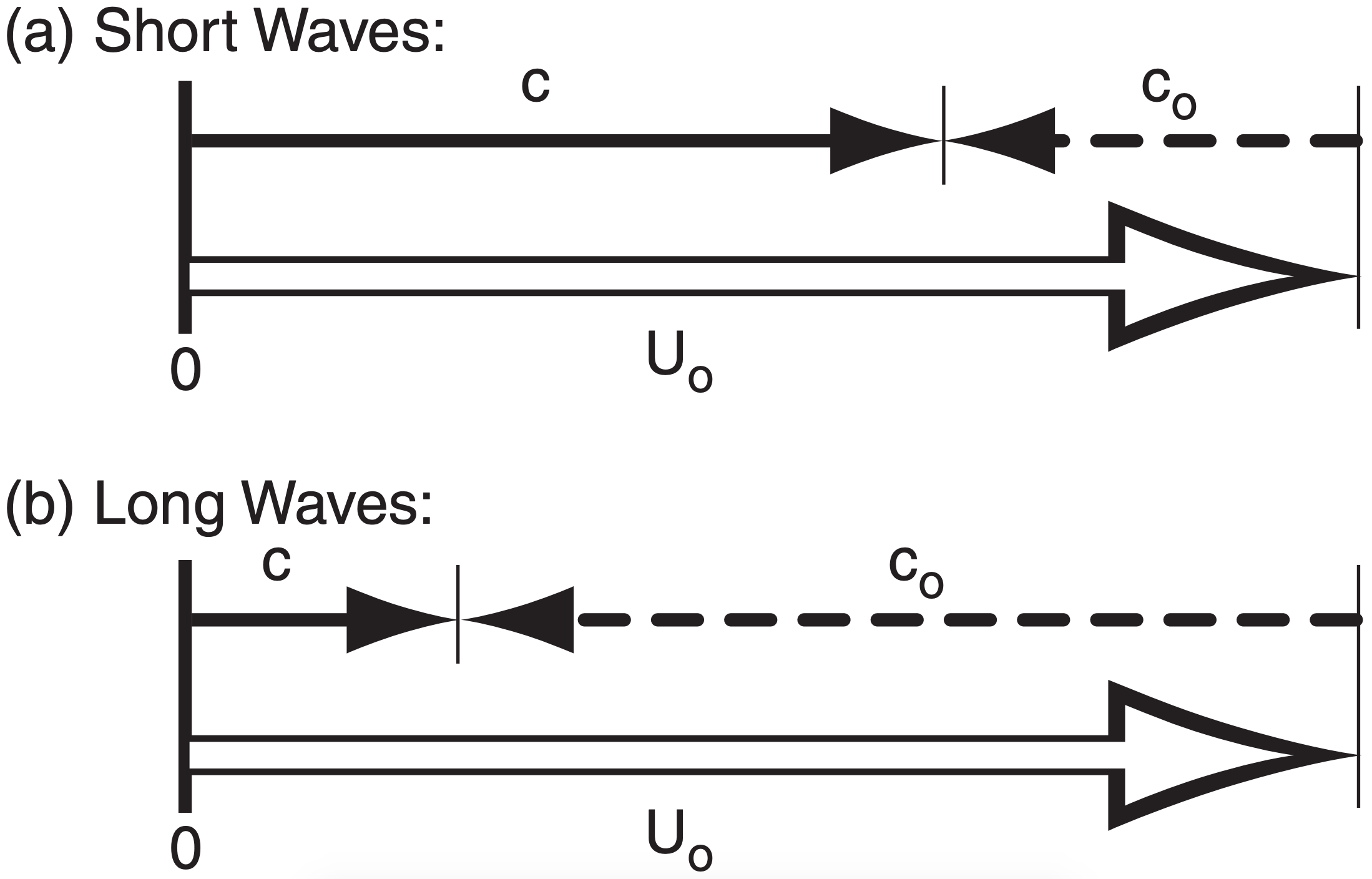
Barotropic Rossby waves can have a range of different wavelengths. But eq. (11.37a) says that different wavelength waves move at different intrinsic phase speeds. Thus, the different waves tend to move apart from each other, which is why eq. (11.37a) is known as a dispersion relationship.
Short waves have slower intrinsic phase speed toward the west, causing the background wind to blow them rapidly toward the east. Long waves, with their faster intrinsic phase speed westbound end up moving more slowly toward the east relative to the ground, as illustrated in Fig. 11.51. The net effect is that short waves move through long waves (see the 3rd Sample Application on the next page).
The speed that Rossby waves transport energy is called the group velocity, cg :
\(\ \begin{align} c_{g}=+\beta \cdot\left(\frac{\lambda}{2 \pi}\right)^{2}\tag{11.38}\end{align}\)
which differs in sign from eq. (11.37a). This causes teleconnections in storminess that moves faster toward the east than the phase speed of the waves.
Suppose the jet-stream axis oscillates north or south some distance y relative to an arbitrary reference latitude as the air flows toward the east (x):
\(\ \begin{align} y=A \cdot \sin (2 \pi \cdot x / \lambda)\tag{a}\end{align}\)
where the wavelength is λ and the meridional amplitude of the wave is A. The jet speed along this wave is M, and the associated wind components (U, V) depend on the local slope s of the wave at location x. From geometry: U2 + V2 = M2 and s = V/U, thus:
\(\ \begin{align} U=M \cdot\left(1+s^{2}\right)^{-1 / 2} \& V=M \cdot s \cdot\left(1+s^{2}\right)^{-1 / 2}\tag{b}\end{align}\)
To find slope s from eq. (a), take the derivative of y:
\(\ \begin{align} s=\partial y / \partial x=(2 \pi A / \lambda) \cdot \cos (2 \pi \cdot x / \lambda)\tag{c}\end{align}\)
Next, change eq. (11.20) from finite difference to partial derivatives:
\(\ \begin{align} \zeta_{r}=\partial V / \partial x-\partial U / \partial y\tag{d}\end{align}\)
But you can expand the last term as follows:
\(\zeta_{r}=\partial V / \partial x-(\partial U / \partial x) \cdot(\partial x / \partial y)\)
where the last factor is just one over the slope:
\(\ \begin{align} \zeta_{r}=\partial V / \partial x-(\partial U / \partial x) \cdot(1 / s)\tag{e}\end{align}\)
Combine eqs. (e, c, & b) to get the desired relative vorticity:
\(\ \begin{align} \zeta_{r}=\frac{-2 \cdot M \cdot A \cdot\left(\frac{2 \pi}{\lambda}\right)^{2} \cdot \sin \left(\frac{2 \pi x}{\lambda}\right)}{\left[1+\left(\frac{2 \pi A}{\lambda}\right)^{2} \cdot \cos ^{2}\left(\frac{2 \pi x}{\lambda}\right)\right]^{3 / 2}}\tag{f}\end{align}\)
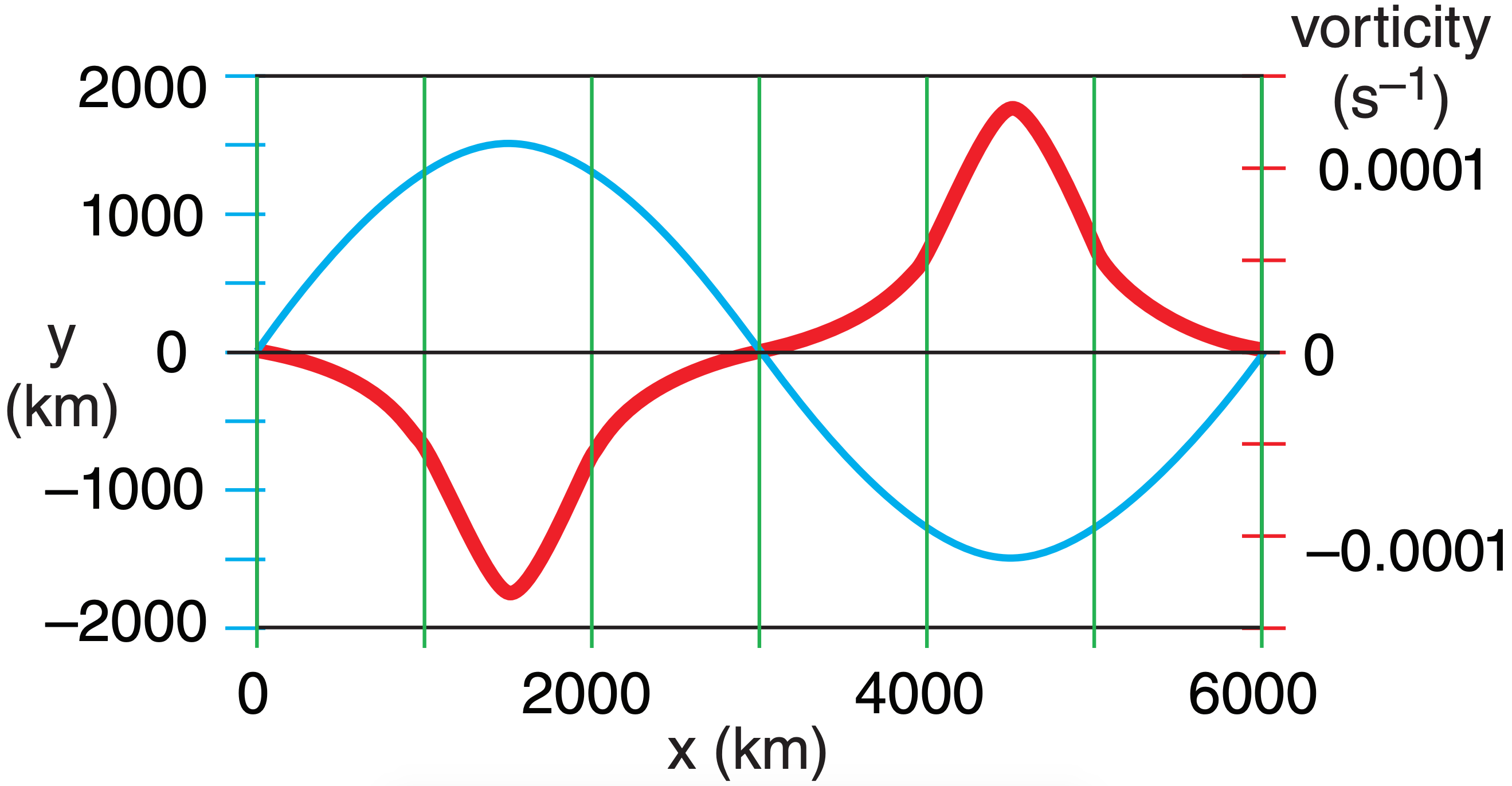
Fig. 11.a illustrates this for a wave with A = 1500 km, λ = 6000 km, & M = 40 m s–1.
Exposition: Some calculus books give equations for the sine-wave radius of curvature R. Using that in |ζr | = 2M/R would give a similar equation for vorticity. The largest vorticities are concentrated near the wave crest and trough, allowing meteorologists to use positive vorticity to help find troughs.
Here is how you can get β using the definition of the Coriolis parameter fc (eq. 10.16):
\(f_{c}=2 \Omega \sin \phi\)
where ϕ is latitude.
Since y is the distance along the perimeter of a circle of radius REarth, recall from geometry that
\(y=R_{\text {Earth}} \cdot \phi\)
for ϕ in radians.
Rearrange this to solve for ϕ, and then plug into the first equation to give:
\(f_{c}=2 \Omega \sin \left(y / R_{\text {Earth}}\right)\)
By definition of β, take the derivative to find
\(\beta=\frac{\partial f_{C}}{\partial y}=\frac{2 \cdot \Omega}{R_{\text {earth}}} \cdot \cos \left(\frac{y}{R_{\text {earth}}}\right)\)
Finally, use the second equation above to give:
\(\ \begin{align} \beta=\frac{2 \cdot \Omega}{R_{\text {earth }}} \cdot \cos \phi\tag{11.35}\end{align}\)
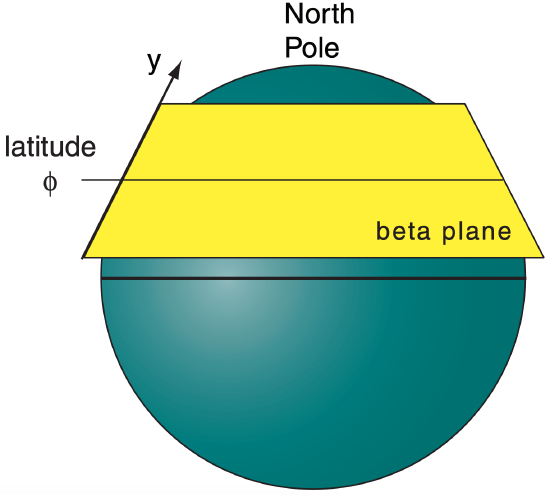
For a small range of latitudes, β is nearly constant. Some theoretical derivations assume constant beta, which has the same effect as assuming that the earth is shaped like a cone. The name for this lamp-shade shaped surface is the beta plane.
Sample Application (§)
The jet stream meanders north and south with barotropic wavelength of 8000 km and amplitude of 1200 km relative to reference latitude 50°N. Winds in this jet are 40 m s–1. Calculate the following for a barotropic wave: beta parameter, phase speeds, and wave translation distance in 12 h. Also, plot the initial and final wave streamlines y’(x’) for x’ of 0 to 11,000 km.
Find the Answer
Given: Uo = 40 m s–1, ϕ =50°, A =1200 km, λ =8000 km, for t = 0 to 12 h
Find: β = ? m–1·s–1, co = ? m s–1, c = ? m s–1 , D = c·∆t ? km translation distance, y’(x’) = ? km.
Apply eq. (11.35):
β = 2.29 x 10-11 ·cos(50°) = 1.47x10–11 m–1·s–1.
Next, apply eq. (11.37a):
\(c_{o}=-\left(1.47 \times 10^{-11} \mathrm{m}^{-1} \mathrm{s}^{-1}\right)\left(\frac{8 \times 10^{6} \mathrm{m}}{2 \pi}\right)^{2}==23.9 \mathrm{m} \mathrm{s}^{-1}\)
Then apply eq. (11.37b):
c = (50 – 23.9) m s–1 = 16.1 m s–1
Wave crest translation distance in 12 h is
D = c·∆t = (16.1 m s–1)·(12h · 3600s/h) = 697.1 km
Finally solve & plot eq. (11.36) for t = 0 to 12 h:
\(y^{\prime} \approx(1200 \mathrm{km}) \cdot \cos \left[2 \pi \cdot\left(\frac{x^{\prime}-(16.1 \mathrm{m} / \mathrm{s}) \cdot t}{8 \times 10^{6} \mathrm{m}}\right)\right]\)
with conversions between m & km, and for s & h.
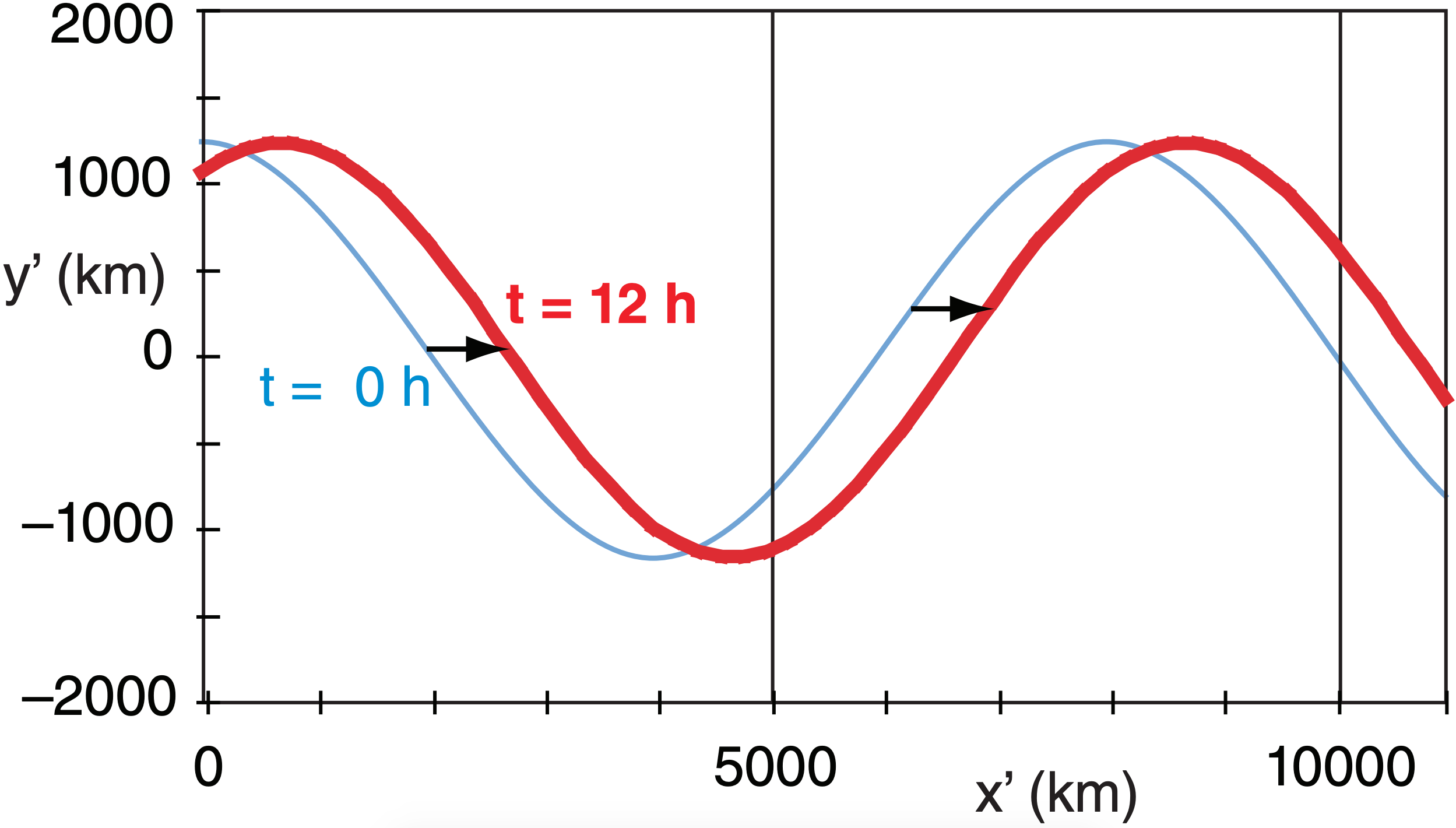
Check: Physics & units are reasonable.
Exposition: The thin blue streamlines plotted above show the path of the 40 m s–1 jet stream, but this path gradually shifts toward the east (thick red streamlines).
Although this Rossby-wave phase speed is much slower than a jet airliner, the wave does not need to land and refuel. Thus, during 24 hours, this long wave could travel about 1,400 km — roughly half the distance between San Francisco, CA & Chicago, IL, USA. Even longer waves can be stationary, and some extremely long waves can retrograde (move in a direction opposite to the background jet-stream flow; namely, move toward the west).
Sample Application (§)
Similar to the previous Sample, but for a short wave with 500 km amplitude and 2000 km wavelength.
Find the Answer
Given: Same, but λ = 2000 km, A = 500 km.
Apply similar equations (not shown here) as before, yielding: β = 1.47x10–11 m–1·s–1, co = –1.5 m s–1 , c = 38.5 m s–1 , and D = 1664 km.
The short-wave streamline plot:
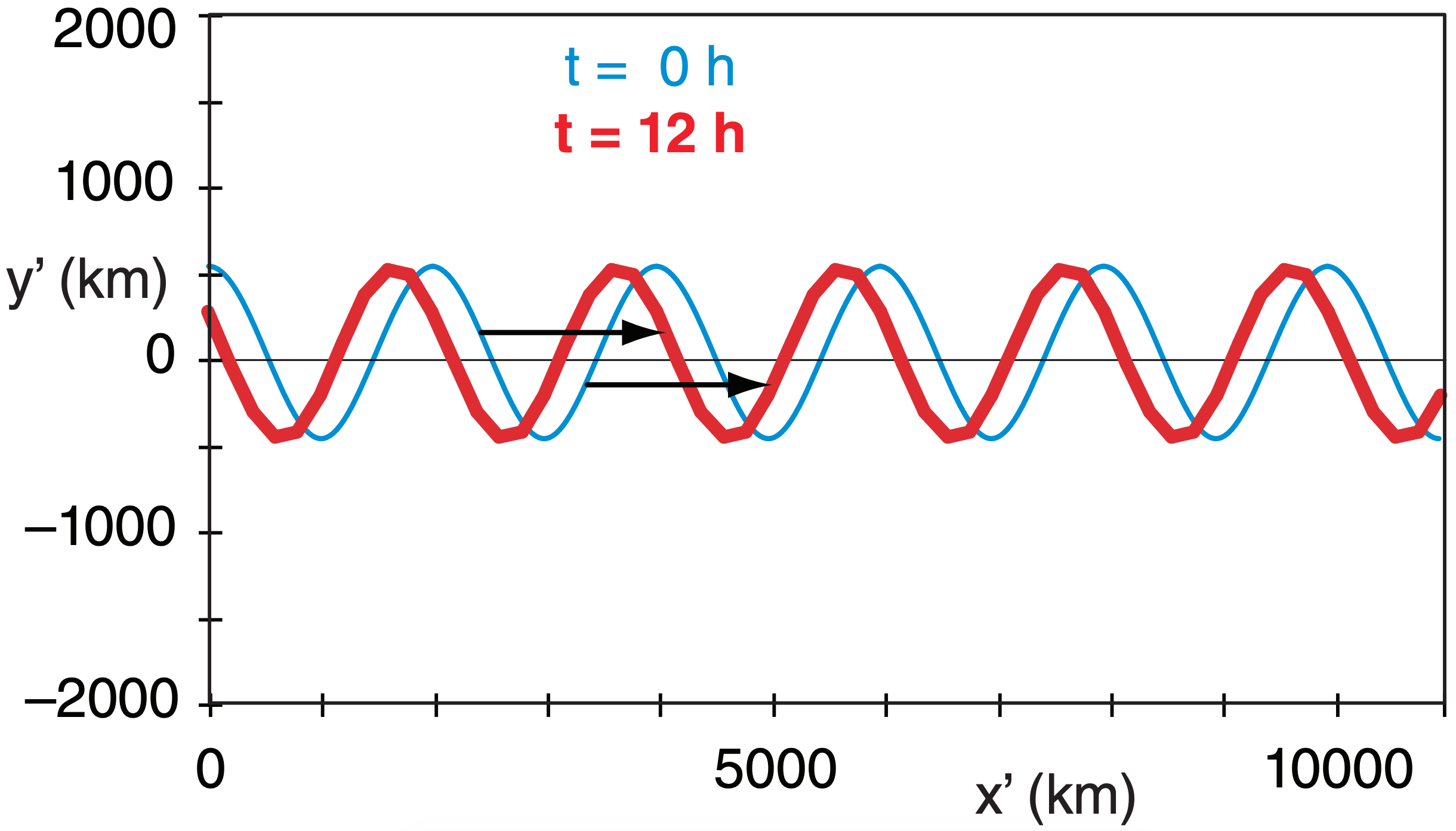
Check: Physics & units reasonable.
Exposition: Short waves move faster than long ones.
Sample Application (§)
Similar to the previous two Sample Applications, but superimpose the long and short waves.
Find the Answer
The combined long- and short-wave streamline plot:
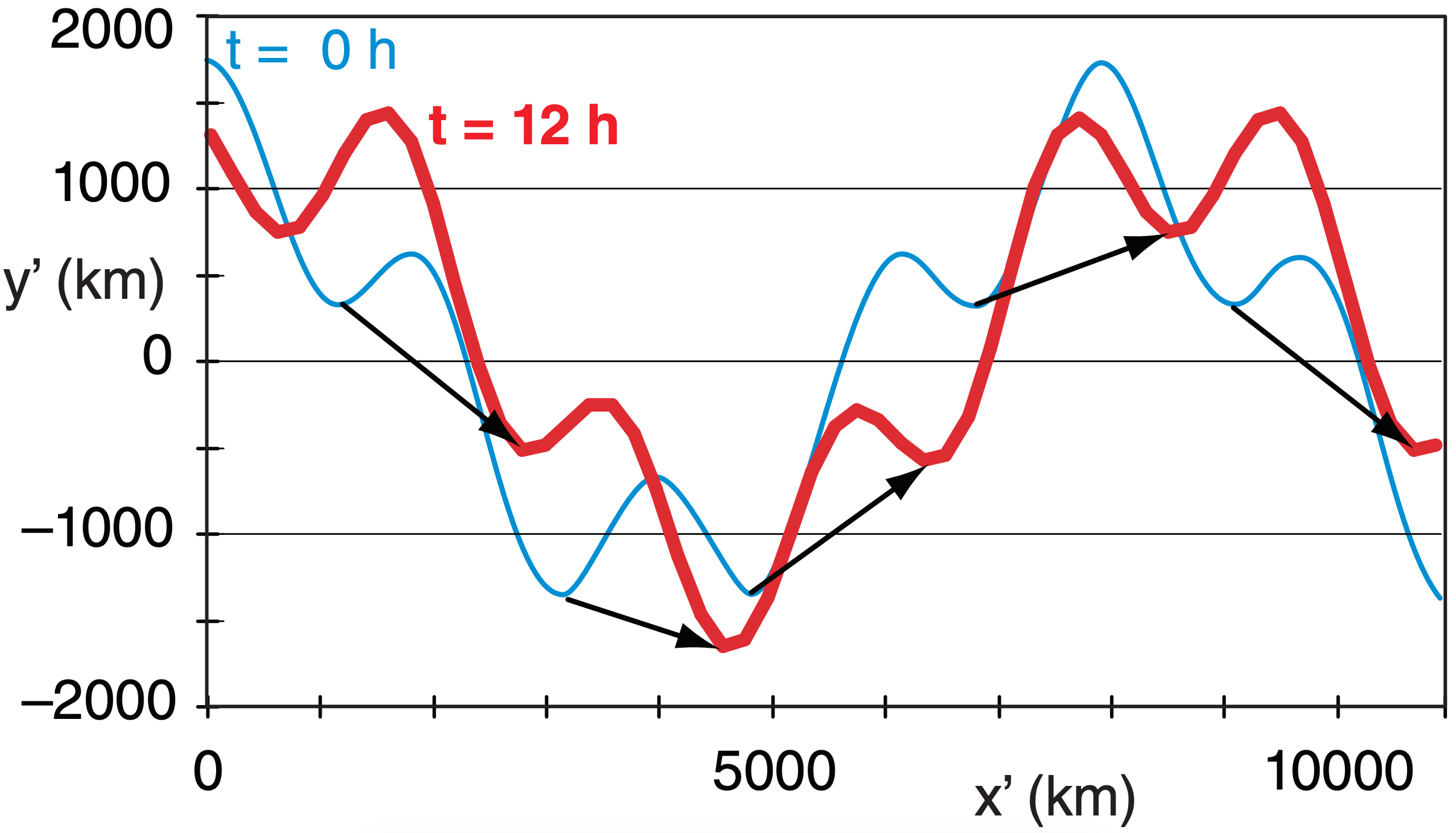
Check: Physics & units reasonable.
Exposition: The short waves move rapidly along the long-wave streamline similar to trains on a track, except that this long-wave track gradually shifts east.
The short waves travel very fast, so they are in and out of any city very quickly. Thus, they cause rapid changes in the weather. For this reason, weather forecasters pay particular attention to short-wave troughs to avoid surprises. Although short waves are sometimes difficult to spot visually in a plot of geopotential height, you can see them more easily on plots of 50 kPa vorticity. Namely, each short-wave trough has a noticeable positive vorticity that can be highlighted or colorized on a forecast map.
11.11.2. Baroclinic Instability
Fig. 11.52 illustrates baroclinic instability using a toy model with thicker atmosphere near the equator and thinner atmosphere near the poles. This mimics the effect of static stability, with cold strongly stable air near the poles that restricts vertical movement of air, vs. warm weakly stable air near the equator that is less limiting in the vertical (see Fig. 5.20 again).
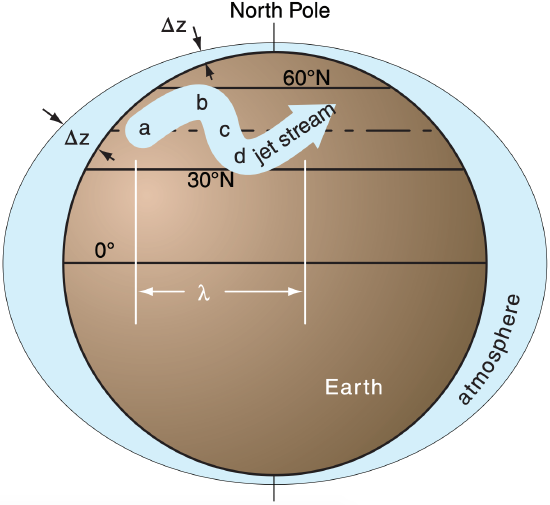

11.11.2.1. Qualitative View
As before, use potential-vorticity conservation:
\(\ \begin{align} \left[\frac{f_{c}+(M / R)}{\Delta z}\right]_{\text {initial}}=\left[\frac{f_{c}+(M / R)}{\Delta z}\right]_{\text {later}}\tag{11.39}\end{align}\)
where M is wind speed, the Coriolis parameter is fc, and the radius of curvature is R. You must include the effective atmospheric thickness ∆z because it varies south to north. This captures baroclinic effects that are intentionally neglected for barotropic instability.
For baroclinic waves, follow the jet stream as was done before for barotropic waves, from location a to location d. All the same processes happen as before, but with an important difference. As the air moves toward location b, not only does fc increase, but ∆z decreases. But ∆z is in the denominator, hence both fc and ∆z tend to increase the potential vorticity. Thus, the curvature M/R must be even more negative to compensate those combined effect. This means the jet stream turns more sharply.
Similarly, at location d, fc is smaller and ∆z in the denominator is larger, both acting to force a sharper cyclonic turn. The net result is that the combined restoring forces are stronger for baroclinic situations, causing tighter turns that create a shorter overall wavelength λ than for barotropic waves.
11.11.2.2. Quantitative View
The resulting north-south displacement y’ for the baroclinic wave is:
\(\ \begin{align} y^{\prime} \approx A \cdot \cos \left(\pi \cdot \frac{z}{Z_{T}}\right) \cdot \cos \left[2 \pi \cdot\left(\frac{x^{\prime}-c \cdot t}{\lambda}\right)\right]\tag{11.40}\end{align}\)
where the tropospheric depth is ZT (≈ 11 km) , the meridional amplitude is A , and where c is phase speed, λ is wavelength, x is distance East, and t is time. Notice that there is an additional cosine factor. This causes the meridional wave amplitude to be zero the middle of the troposphere, and to have opposite signs at the top and bottom.
[ALERT: this is an oversimplification. Waves in the real atmosphere aren’t always 180° out of phase between top and bottom of the troposphere. Nonetheless, this simple approach gives some insight into the workings of baroclinic waves.]
The intrinsic phase speed co for the baroclinic wave is:
\(\ \begin{align} c_{o}=\frac{-\beta}{\pi^{2} \cdot\left[\frac{4}{\lambda^{2}}+\frac{1}{\lambda_{R}^{2}}\right]}\tag{11.41}\end{align}\)
where eq. (11.35) gives β, wavelength is λ, and eq. (11.12) gives the internal Rossby deformation radius λR.
The influence of static stability is accounted for in the Brunt-Väisälä frequency NBV, which is a factor in the equation for Rossby deformation radius λR (eq. 11.12). Recall from the Atmospheric Stability chapter that NBV = [ (|g|/Tv) · (Γd + ∆T/∆z) ]1/2 , where gravitation acceleration is |g| = 9.8 m s–2, absolute virtual temperature is Tv (where Tv = T for dry air), dry adiabatic lapse rate is Γd = 9.8 °C km–1 = 0.0098 K m–1, and ∆T/∆z is the change of air temperature with height.
As before, the phase speed relative to the ground is:
\(\ \begin{align} c=U_{o}+c_{o}\tag{11.42}\end{align}\)
Although many different wavelengths λ are possible, the dominant wavelength (i.e., the wave for which amplitude grows the fastest) is roughly:
\(\ \begin{align} \lambda_{d} \approx 2.38 \cdot \lambda_{R}\tag{11.43}\end{align}\)
where λR is the internal Rossby radius of deformation (eq. 11.12). Typical values are λd ≈ 3 to 4 Mm.
Sample Application(§)
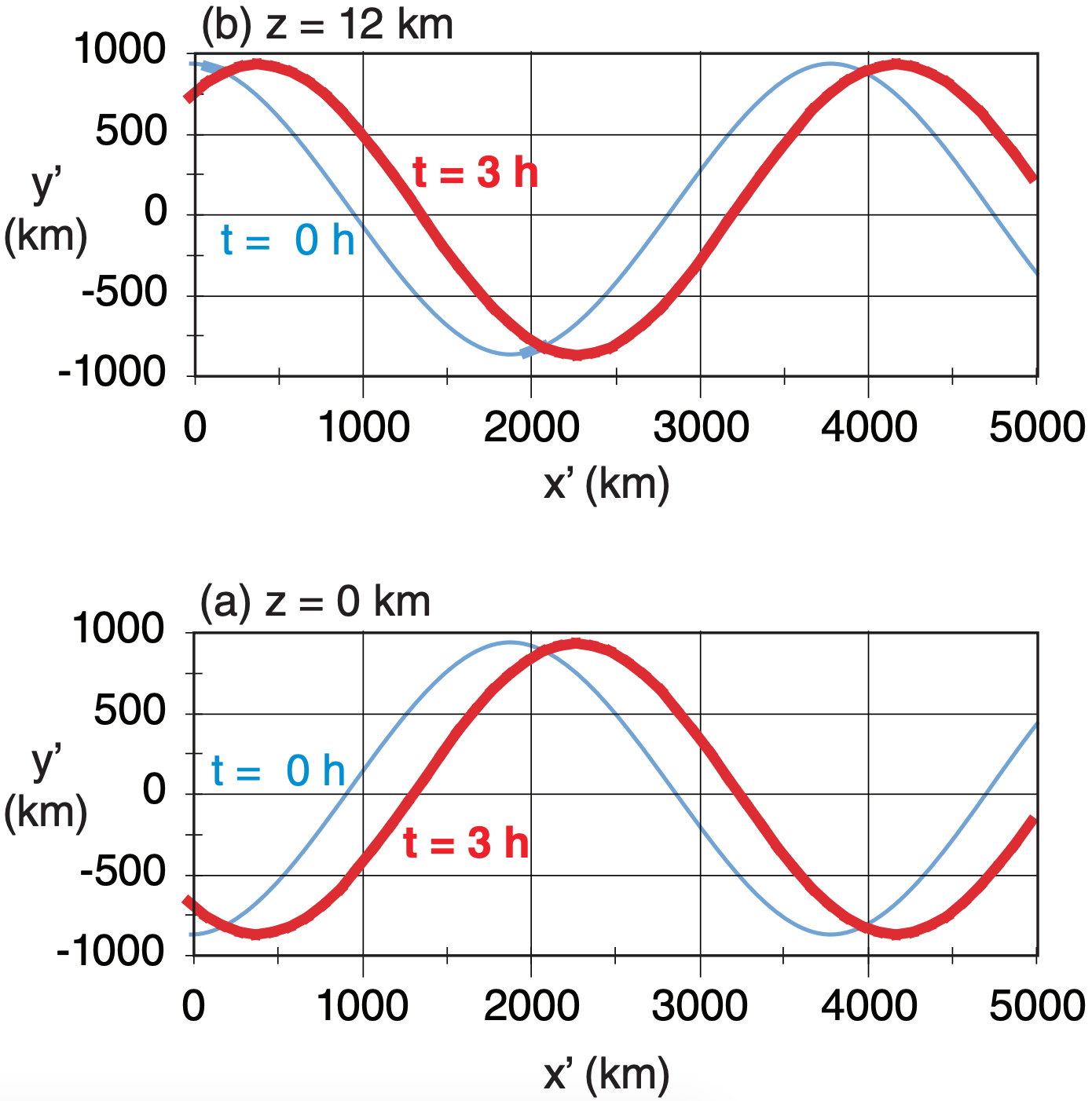
The jet stream meanders north and south with amplitude of 900 km relative to reference latitude 50°N. Winds in this jet are 40 m s–1. Temperature decreases 50°C across 12 km thick troposphere, with average temperature –20°C. Calculate the following for a baroclinic wave: Brunt-Väisälä frequency, internal Rossby radius, dominant wavelength, phase speeds, and wave translation distance in 3 h. Also, plot the initial and final wave streamlines y’(x’) at both z = 0 and z = 12 km for x’ ranging 0 to 5,000 km. β = 1.47x10–11 m–1·s–1.
Find the Answer
Given: Uo = 40 m s–1, ϕ =50°, A =900 km, Tavg = 253 K, ∆T/∆z = –50K/(12 km), β = 1.47x10–11 m–1·s–1, for z=1 & 12 km, t = 0 & 3 h
Find: NBV = ? s–1, λR = ? km, λ = ? km, co = ? m s–1, c = ? m s–1 , y’(x’) = ? km.
Get the NBV eq. from the right column of this page.
\(N_{B V}=\left[\frac{\left(9.8 \mathrm{ms}^{-2}\right)}{253 \mathrm{K}}\left(\frac{-50 \mathrm{K}}{1.2 \times 10^{4} \mathrm{m}}+0.0098 \frac{\mathrm{K}}{\mathrm{m}}\right)\right]^{1 / 2}\)
NBV = 0.0148 s–1
Apply eq. (10.16):
\(f_{c}=\left(1.458 \times 10^{-4} s^{-1}\right) \cdot \sin \left(50^{\circ}\right)=1.117 \times 10^{-4} \mathrm{s}^{-1}\)
Apply eq. (11.12):
\(\lambda_{R}=\frac{\left(0.0148 \mathrm{s}^{-1}\right) \cdot(12 \mathrm{km})}{1.117 \times 10^{-4} \mathrm{s}^{-1}}=1590 . \mathrm{km}\)
Apply eq. (11.43):
λ = λd = 2.38 λR = 3784. km
Apply eq. (11.41):
\(c_{o}=\frac{-\left(1.47 \times 10^{-11} \mathrm{m}^{-1} \mathrm{s}^{-1}\right)}{\pi^{2} \cdot\left[\frac{4}{\left(3.784 \times 10^{6} \mathrm{m}\right)^{2}}+\frac{1}{\left(1.59 \times 10^{6} \mathrm{m}\right)^{2}}\right]}\)
= –2.21 m s–1
Apply eq. (11.42):
c = ( 40 – 2.21 )m s–1 = 37.8 m s–1
Use eq. (11.40) for z = 0, 12 km, and t = 0, 3 h:
\(y^{\prime} \approx(900 \mathrm{km}) \cos \left(\frac{\pi \cdot z}{12 \mathrm{km}}\right) \cos \left[2 \pi\left(\frac{x^{\prime}-(37.8 \mathrm{m} / \mathrm{s}) \cdot t}{3784 \mathrm{km}}\right)\right]\)
The results are plotted at right:
Check: Physics & units are reasonable.
Exposition: The Rossby wave at z = 12 km is indeed 180° out of phase from that at the surface. Namely, an upper-level ridge is above a surface trough. In the mid-troposphere (z ≈ 6 km) the baroclinic wave has zero amplitude (not shown).
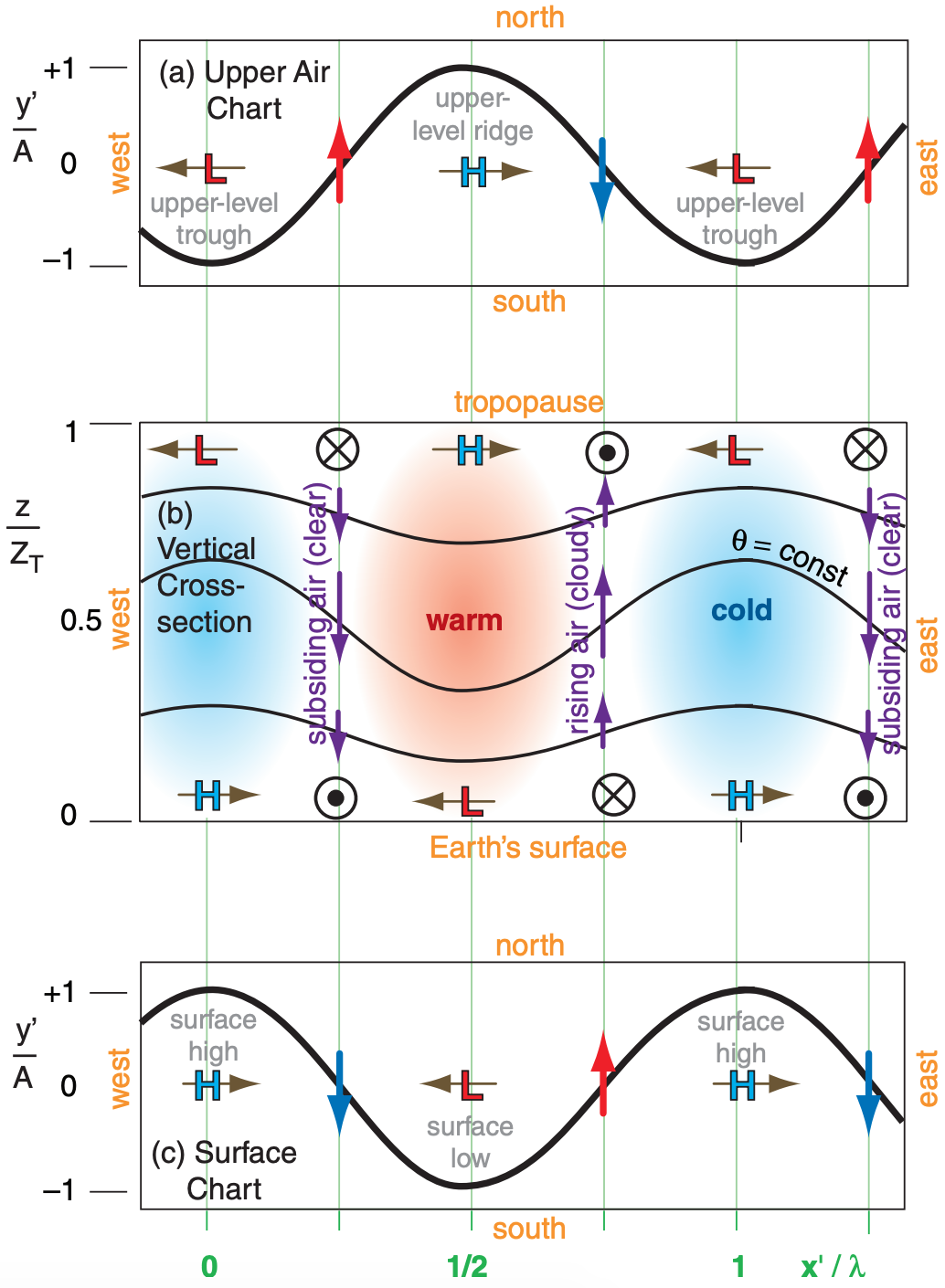
Baroclinic waves perturb many variables relative to their average background states. Represent the perturbation by e’ = e – ebackground for any variable e. Variables affected include:
y’ = meridional streamline displacement north,
(u’, v’, w’) = wind components,
θ’ = potential temperature,
p’ = pressure, and
η’ = vertical displacement.
Independent variables are time t and east-west displacement x’ relative to some arbitrary location.
Let:
\(\ \begin{align} a=\pi \cdot z / Z_{T}\tag{11.44}\end{align}\)
\(\ \begin{align} b=2 \pi \cdot\left(x^{\prime}-c \cdot t\right) / \lambda\tag{11.45}\end{align}\)
Thus:
\(\ \begin{align} \begin{array}{ll}y^{\prime}= & \hat{Y} \cdot \cos (a) \cdot \cos (b) \\ \eta^{\prime}= & \hat{\eta} \cdot \sin (a) \cdot \cos (b) \\ \theta^{\prime}= & -\hat{\theta} \cdot \sin (a) \cdot \cos (b) \\ p^{\prime}= & \hat{P} \cdot \cos (a) \cdot \cos (b) \\ u^{\prime}= & \hat{U} \cdot \cos (a) \cdot \cos (b) \\ v^{\prime}= & -\hat{V} \cdot \cos (a) \cdot \sin (b) \\ w^{\prime}= & -\hat{W} \cdot \sin (a) \cdot \sin (b)\end{array}\tag{11.46}\end{align}\)
Each of the equations above represents a wave, where the wave amplitude is indicated by the factor with the caret (^) over it. These amplitudes are always positive. For Northern Hemispheric baroclinic waves, the amplitudes are:
\(\ \begin{align} \begin{array}{\\} \hat{Y} = & A \\
\hat{\eta}=&\frac{A \cdot \pi \cdot f_{c} \cdot\left(-c_{0}\right)}{Z_{T}} \cdot \frac{1}{N_{B V}^{2}} \\
\hat{\theta}=&\frac{A \cdot \pi \cdot f_{c} \cdot\left(-c_{0}\right)}{Z_{T}} \cdot \frac{\theta_{0}}{g} \\
\hat{P}=&A \cdot \rho_{o} \cdot f_{c} \cdot\left(-c_{o}\right) \\
\hat{U}=&\left[\frac{A \cdot 2 \pi \cdot\left(-c_{0}\right)}{\lambda}\right]^{2} \cdot \frac{1}{A \cdot f_{c}} \\
\hat{V}=&\frac{A \cdot 2 \pi \cdot\left(-c_{0}\right)}{\lambda}\\
\hat{W}=&\frac{A \cdot 2 \pi \cdot\left(-c_{0}\right)}{\lambda} \cdot \frac{\pi \cdot\left(-c_{0}\right) \cdot f_{c}}{Z_{T} \cdot N_{B V}^{2}}\end{array}\tag{11.47}\end{align}\)
where ρo is average density of air at height z, and intrinsic phase speed co is a negative number. A (= north-south displacement) depends on the initial disturbance.
Any atmospheric variable can be reconstructed as the sum of its background and perturbation values; for example: U = Ubackground + u’. Background states are defined as follows.
Ubackground = Ug is the geostrophic (jet-stream) wind.
Vbackground = Wbackground = 0.
Pbackground decreases with increasing height according to the hydrostatic equation (Chapter 1).
θbackground increases linearly as altitude increases as was assumed to create a constant value of NBV.
Ybackground corresponds to the latitude of zeroperturbation flow, which serves as the reference latitude for calculation of fc and β.
Background state for η is the altitude z in eq. (11.44).
All variables listed at left interact together to describe the wave. The result is sketched in Fig. 11.53. Although the equations at left look complicated, they are based on a simplified description of the atmosphere. They neglect clouds, turbulence, latent heating, meridional wave propagation, and nonlinear effects. Nonetheless, the insight gained from this simple model helps to explain the behavior of many of the synoptic weather patterns that are covered in the Extratropical Cyclones chapter.
Sample Application
Given A = 900 km, λ = 3784 km, co = –2.21 m s–1, ZT = 12 km, fc = 1.117x10–4 s–1, ρo = 1 kg m–3, NBV = 0.0148 s–1, and |g|/θo = 0.038 m s–2 K–1. Find the amplitudes for all baroclinic wave variables.
Find the Answer
Given: A = 900 km, λ = 3784 km, co = –2.21 m s–1, ZT = 12 km, fc = 1.117x10–4 s–1, ρo = 1 kg m–3, NBV = 0.0148 s–1, and |g|/θo = 0.038 m s–2 K–1.
Find: \(\hat{Y}, \hat{\eta}, \hat{\theta}, \hat{P}, \hat{U}, \hat{V}, \hat{W}\)
Apply eqs. (11.47). \( \hat{Y}=A=900 \mathrm{km}\)
\(\hat{\eta}=(900 \mathrm{km}) \cdot \pi \cdot\left(1.117 \times 10^{-4} \mathrm{s}^{-1}\right) \cdot\left(2.21 \mathrm{m} \mathrm{s}^{-1}\right) /
\left[(12 \mathrm{km}) \cdot\left(0.0148 \mathrm{s}^{-1}\right)^{2}\right]=265.5 \mathrm{m}\)
\(\hat{\theta}_{,}=1.53 \mathrm{K}\)
\(\hat{P}=0.222 \mathrm{kPa}\)
\(\hat{U}=0.109 \mathrm{m} \mathrm{s}^{-1}\)
\(\hat{V}=3.30 \mathrm{m} \mathrm{s}^{-1}\)
\(\hat{W}=0.000974 \mathrm{m} \mathrm{s}^{-1}=3.5 \mathrm{m} \mathrm{h}^{-1}\)
Check: Physics & units are reasonable.
Exposition: Compared to the 40 m s–1 jet-stream background winds, the U perturbation is small. In fact, many of these amplitudes are small. They would be larger for larger A and for shorter wavelengths and a shallower troposphere.
11.11.3. Meridional Transport by Rossby Waves
11.11.3.1. Heat Transport Meridionally
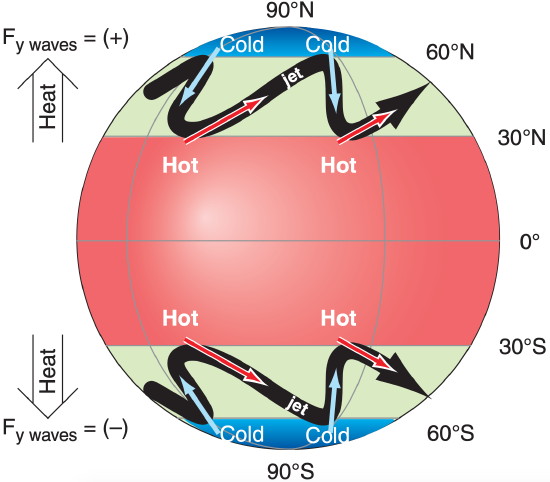
As the jet stream meanders north and south while encircling the earth with its west-to-east flow, its temperature changes in response to the regions it flows over (Fig. 11.54). For example, ridges in the planetary wave are where the jet stream is closest to the poles. This air is flowing over colder ground, and is also getting little or no direct solar heating because of the low sun angles (particularly in winter). As a result, the air becomes colder when near the poles than the average jet-stream temperature.
The opposite temperature change occurs in the troughs, where the jet stream is closest to the equator. The air near troughs is flowing over a warmer Earth surface where significant amounts of heat are moved into the jet stream via convective clouds and solar radiation. Define T’ as the amount that the temperature deviates from the average value, so that positive T’ means warmer (in the troughs), and negative T’ means colder (in the ridges) than average.
Define v’ as deviation in meridional velocity relative to the mean (V = 0). Positive v’ occurs where meandering air has a component toward the north, and negative v’ means a component toward the south.
Northward movement (v’ = +) of warm air (T’ = +) in the N. Hemisphere contributes to a positive (northward) heat flux v’T’. This is a kinematic flux, because units are K·m/s. Similarly, southward movement (v’ = –) of cold air (T’ = –) also contributes to a positive heat flux v’T’ (because negative times negative = positive). Adding all the contributions from N different parts of the meandering jet stream gives an equation for the mean meridional heat flux Fy caused by Rossby waves:
\(F_{y \text { waves }}=(1 / N) \cdot \Sigma\left(v^{\prime} \cdot T^{\prime}\right)\)
This flux is positive (negative) in the N. (S.) Hemispheres. Thus, for both hemispheres, Rossby waves move heat from the tropics toward the poles.
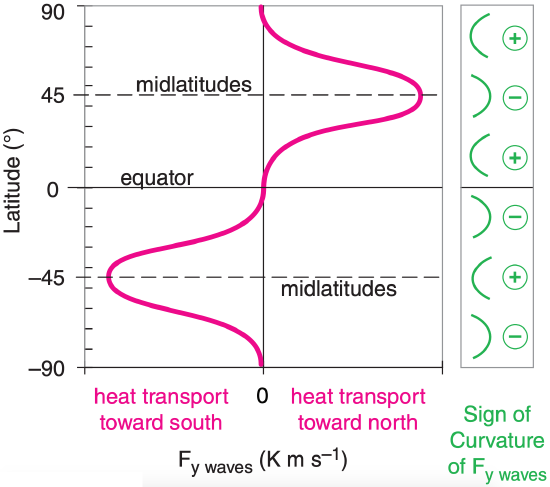
The largest magnitudes of v’ and T’ occur at midlatitudes, where the jet stream has the largest meridional wind speeds co-located in the region of greatest meridional temperature gradient (Fig. 11.8). Fig. 11.55 shows a sketch of Fy waves vs. latitude. When this line is concave to the right, it indicates positive curvature (Curv). Concave to the left is negative curvature. Curvature of Fy waves will be used later.
11.11.3.2. Momentum Transport Meridionally
Even if the atmosphere were calm with respect to the Earth’s surface, the fact that the Earth is rotating implies that the air is also moving toward the east. Latitude circles near the equator have much larger circumference than near the poles, hence air near the equator must be moving faster toward the east.
As Rossby waves move some of the tropical air poleward (positive v’ in N. Hem.; negative v’ in S. Hem.), conservation of U angular momentum requires the speed-up (positive U-wind perturbation: u’) as the radius from Earth’s axis decreases. Similarly, polar air moving equatorward must move slower (negative u’ relative to the Earth’s surface).
The north-south transport of U momentum is called the average kinematic momentum flux \(\overline{u^{\prime} v^{\prime}}\):
\(\overline{u^{\prime} v^{\prime}}=(1 / N) \cdot \Sigma\left(u^{\prime} \cdot v^{\prime}\right)\)
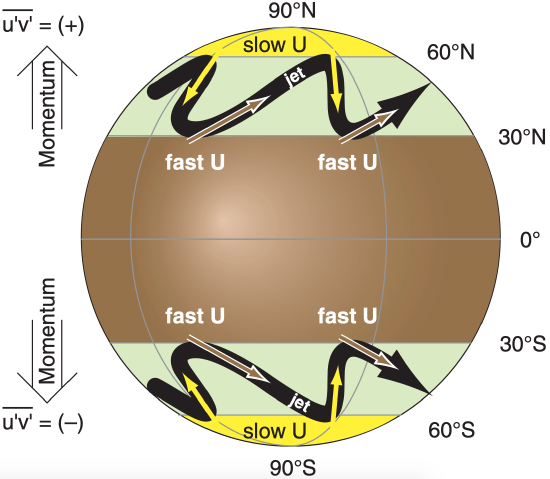
For example, consider a N. Hemisphere Rossby-wave. Poleward motion (positive \(v^{\prime}\) ; see brown arrows in Fig. 11.56) transports faster U winds (i.e., positive \(\ u^{\prime}\)), causing positive \(u^{\prime} v^{\prime}\). Similarly, equatorward motion (negative \(\ v^{\prime}\); see yellow arrows) transports slower U winds (i.e., negative \(\ u^{\prime}\)), so again the product is positive \(u^{\prime} v^{\prime}\). Averaging over all such segments of the jet stream gives positive \(\overline{u^{\prime} v^{\prime}}\) in the N. Hemisphere, which you can interpret as transport of zonal momentum toward the N. Pole by Rossby waves. In the Southern Hemisphere, \(\overline{u^{\prime} v^{\prime}}\) is negative, which implies transport of U momentum toward the S. Pole.
To compensate for the larger area of fast U winds (brown in Fig. 11.56) relative to the smaller area of slower U winds (yellow in Fig. 11.56), one can multiply the angular momentum by a = cos(ϕs)/cos(ϕd):
\(\ \begin{align} a \cdot u^{\prime} \approx \Omega \cdot R_{\text {earth}} \cdot\left[\frac{\cos ^{2} \phi_{s}}{\cos \phi_{d}}-\cos \phi_{d}\right] \cdot \frac{\cos \phi_{s}}{\cos \phi_{d}}\tag{11.48}\end{align}\)
where subscript s represents source location, d is destination, and Ω·REarth = 463.4 m s–1 as before.
Sample Application
Find the weighted zonal velocity perturbation for air arriving at 50°N from 70°N.
Find the Answer
Given: ϕs = 70°N, ϕd = 50°N
Find: a·u’ = ? m s–1
Apply eq. (11.48): \(a \cdot u^{\prime}=(463.4 \mathrm{m} / \mathrm{s}) \cdot\left[\frac{\cos ^{2}\left(70^{\circ}\right)}{\cos \left(50^{\circ}\right)}-\cos \left(50^{\circ}\right)\right] \frac{\cos \left(70^{\circ}\right)}{\cos \left(50^{\circ}\right)}\)
= – 113.6 m s–1
Check: Physics reasonable, but magnitude too large.
Exposition: The negative sign means air from 70°N is moving slower from the west than any point at 50°N on the Earth’s surface is moving. Thus, relative to the Earth, the wind is from the east.
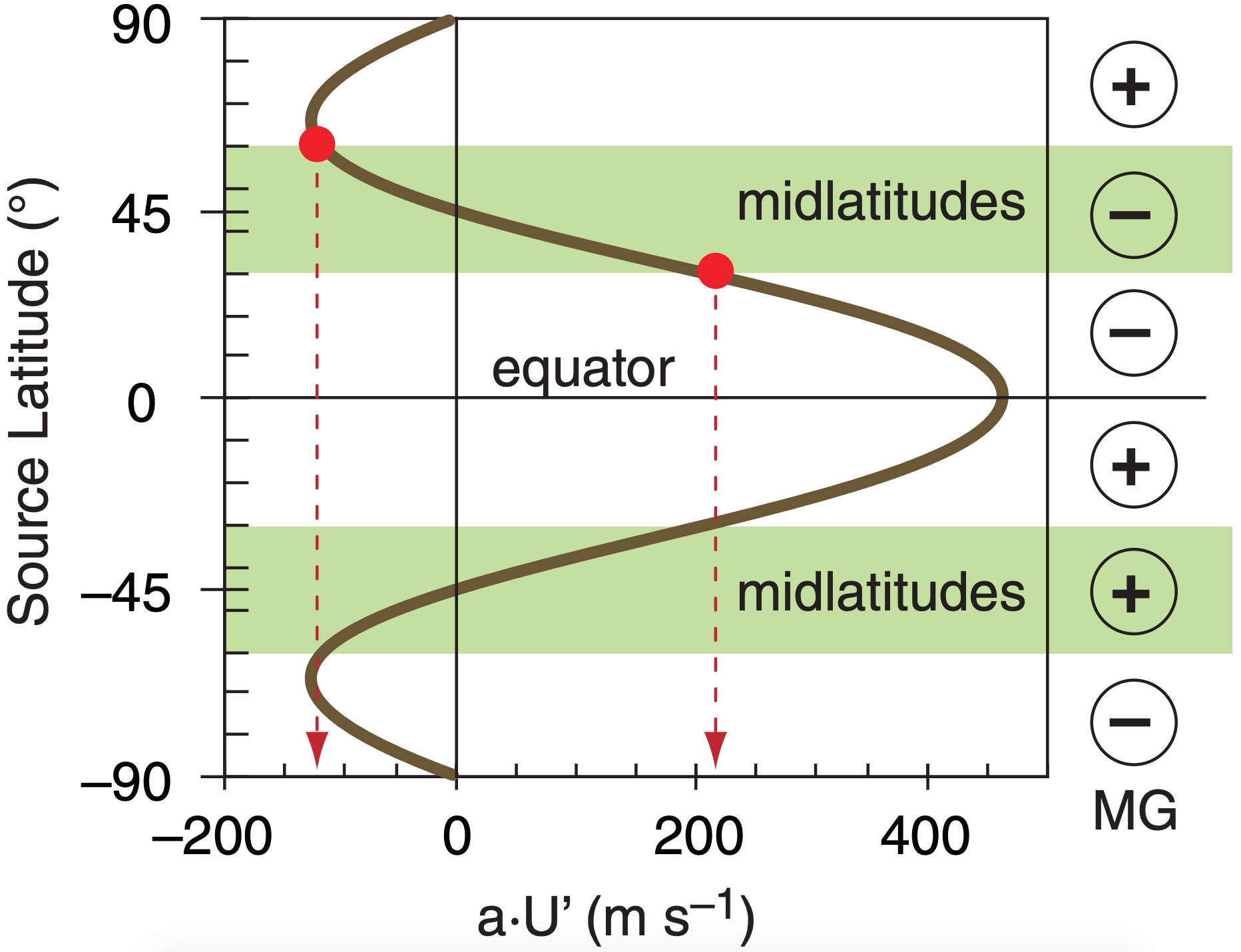
For example, consider the weighted zonal velocity a·U’ that reaches destination latitude 45° from other source latitudes, as sketched in Fig. 11.57. Air starting from 30° has much larger magnitude |a·U’| than does air starting from 60°. (ALERT: Angularmomentum conservation gives unrealistically large velocities, but is qualitatively informative.)
The change of weighted Rossby-wave momentum flux with latitude is
\(\ \begin{align} M G=\Delta \overline{u^{\prime} v^{\prime}} / \Delta y\tag{11.49}\end{align}\)
where MG is the north-south gradient of zonal momentum. From Fig. 11.57 we infer that MG is negative (positive) in N. (S.) Hemisphere midlatitudes. This meridional gradient implies that excess zonal momentum from the tropics is being deposited at midlatitudes by the Rossby waves.
Rossby waves that transport U momentum poleward have a recognizable rounded-sawtooth shape, as sketched in Figs. 11.56 & 11.58. Specifically, the equatorward-moving portions of the jet stream are aligned more north-south (i.e., are more meridional), and sometimes even tilt backwards (toward the west as it moves toward the equator). The poleward-moving portions of the jet are more zonal (west to east).



