11.8: Jet Streams

In the winter hemisphere there are often two strong jet streams of fast west-to-east moving air near the tropopause: the polar jet stream and the subtropical jet stream (Figs. 11.34 & 11.35).

Figure 11.34 Sketch of jet streams, representing a snapshot.

Figure 11.35 Simplified vertical cross-section. Thick solid line is the tropopause. Darker shading indicates faster winds (perpendicular to the page). This is a snapshot, not a climatological average; hence, the polar jet and polar front can be seen.

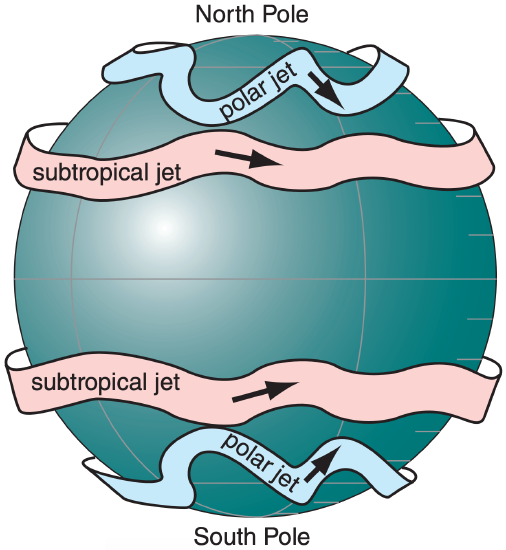
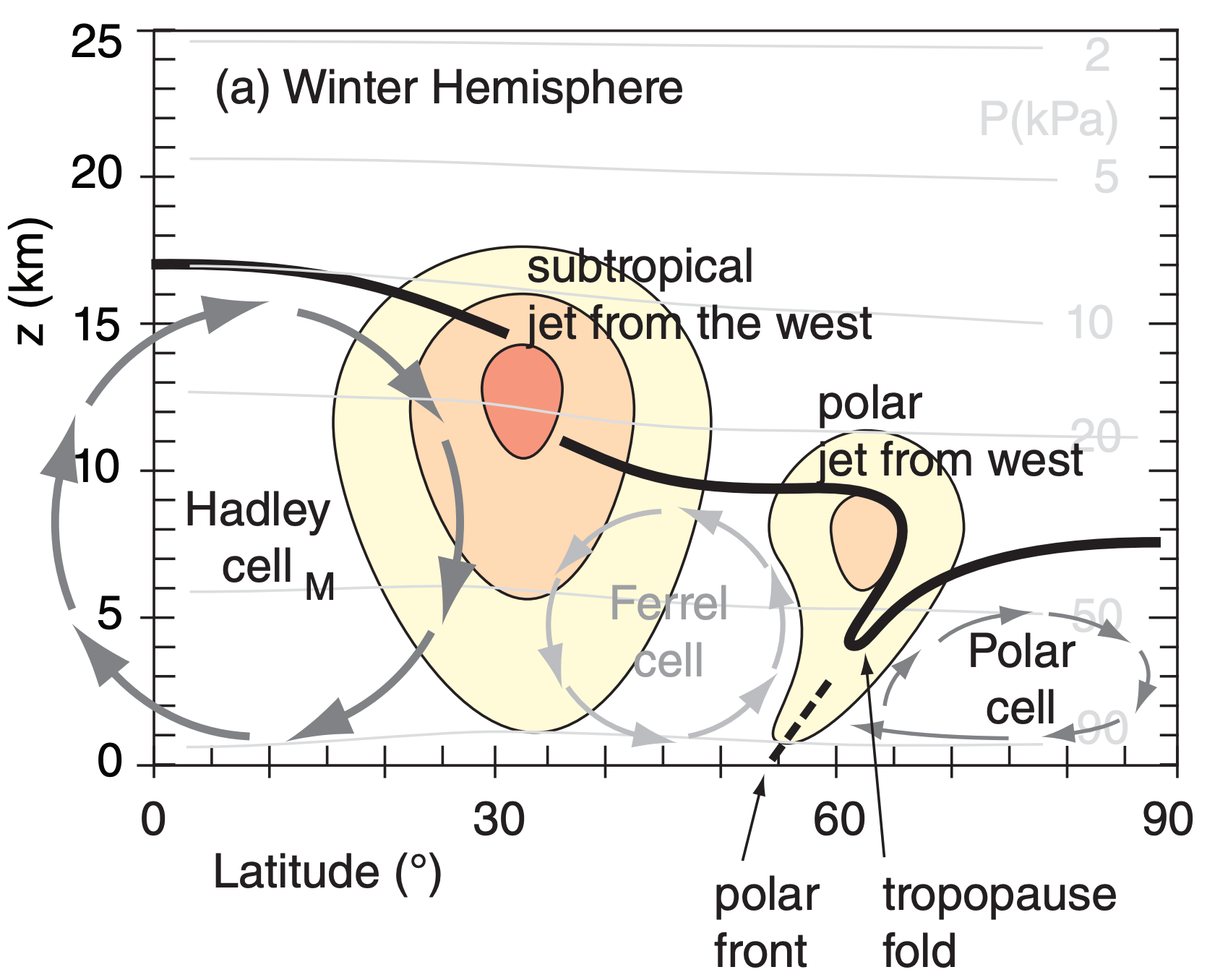
The subtropical jet is centered near 30° latitude in the winter hemisphere. This jet: (1) is very steady; (2) meanders north and south a bit; (3) is about 10° latitude wide (width ≈1,000 km); and (4) has seasonal-average speeds of about 45 m s^–1 over the Atlantic Ocean, 55 to 65 m s^–1 over Africa and the Indian Ocean, and 60 to 80 m s^–1 over the western Pacific Ocean. The core of fast winds near its center is at 12 km altitude (Fig. 11.35). It is driven by outflow from the top of the Hadley cell, and is affected by both Coriolis force and angular-momentum conservation.

The polar jet is centered near 50 to 60° latitude in the winter hemisphere. The polar jet: (1) is extremely variable; (2) meanders extensively north and south; (3) is about 5° latitude wide; and (4) has widely varying speeds (25 to 100 m s^–1) driven by varying horizontal temperature gradients. The core altitude is about 9 km. This jet forms over the polar front — driven by thermal-wind effects due to the strong horizontal temperature contrast across the front.

When meteorological data are averaged over 30 years, the subtropical jet shows up clearly in the data (e.g., Fig. 11.36) because it is so steady. However, the polar jet disappears because it meanders and shifts so extensively that it is washed out by the long-term average. Nonetheless, these transient meanders of the polar jet (troughs and ridges in the Rossby waves) are extremely important for mid-latitude cyclone formation and evolution (see the Extratropical Cyclone chapter).

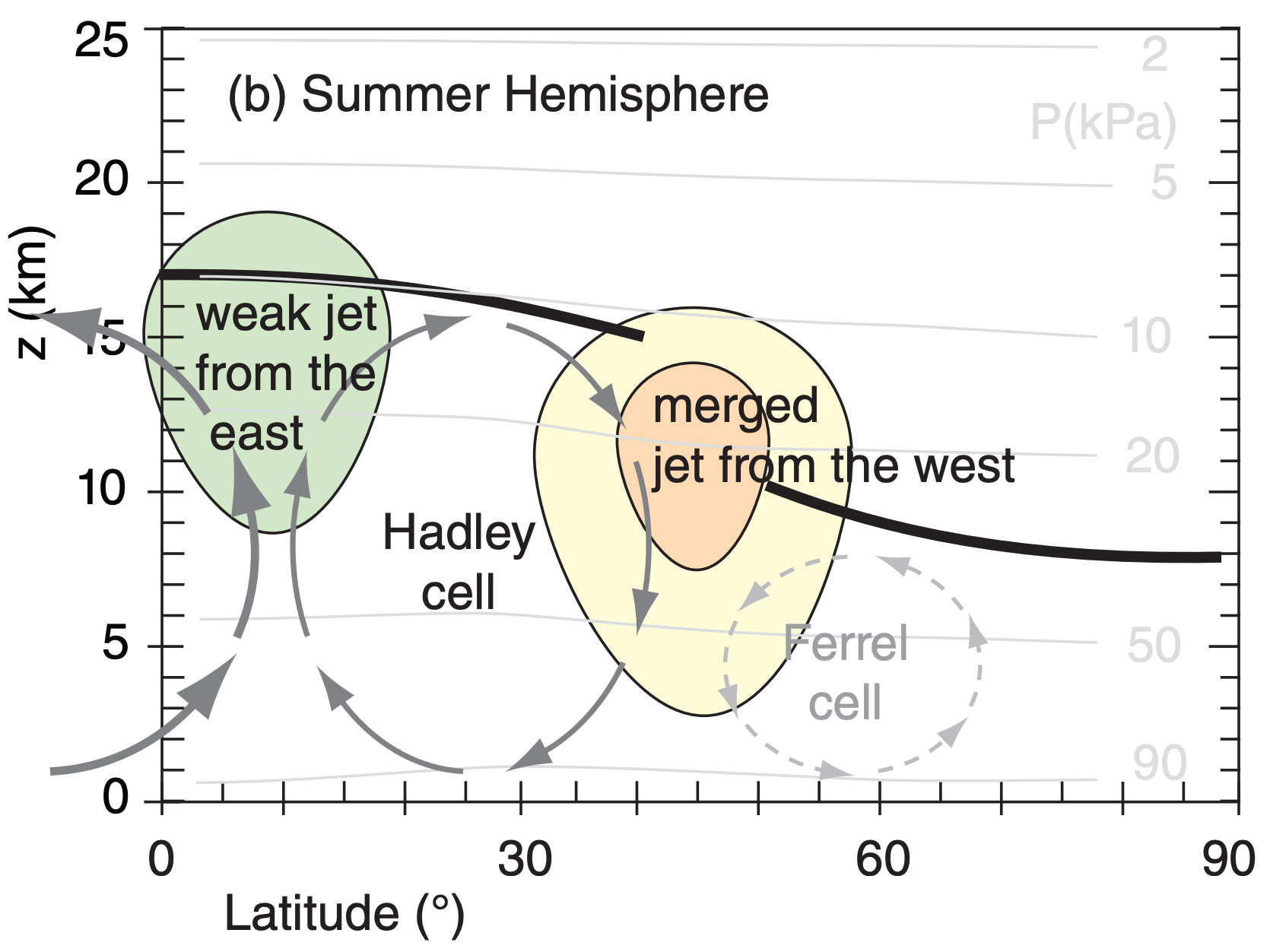
In the summer hemisphere, the jets from the west have merged (Figs. 11.35b and 11.36), and the winds are slower because of the weaker temperature contrast between the equator and the warm pole. Core wind speeds in the jet are 0 to 10 m s^–1 in N. Hemisphere summer, and 5 to 45 m s^–1 in S. Hemisphere summer. This core shifts poleward to be centered near 40° to 45° latitude. A weak jet from the east is centered at roughly 10° latitude in the summer hemisphere.

INFO • Jet Stream Aspect Ratio

Jet streams in the real atmosphere look very much like the thin ribbons of fast-moving air, as sketched in Fig. 11.34. Jet vertical thickness (order of 5 to 10 km) is much smaller than their horizontal width (order of 1000 to 2000 km). Namely, their aspect ratio (width/ thickness) is large. Figures such as 11.35 are intentionally distorted to show vertical variations better.

Figure 11.36 Zonal (U) component of winds (m s^–1) at 20 kPa isobaric surface (near the tropopause) for (a) January, and (b) July, averaged over the 30 years of 1981 to 2010. Contour interval is 10 m s^–1. All negative (east) winds are lightly hatched in red, and are indicated with white arrows. Positive (west) winds are indicated with black arrows, and are shaded in blue with isotachs at 40 and 60 m s^–1. In polar regions, the tropopause is relatively low (at about 8 km altitude, where P ≈ 35 kPa; see Table 6-1 in Chapter 6), so 20 kPa is well above the tropopause (compare the 20 kPa winds here with tropopause winds sketched in Fig. 11.3b). [NCAR/NCEP Reanalysis.]

11.8.1. Baroclinicity & the Polar Jet

Figure 11.37 Vertical cross sections through the atmosphere on January 2003. (a) isotherms T (°C), (b) isobars P (kPa), (c) isotachs of the zonal wind U (m s^–1). The tropopause is indicated by a heavy solid line. For this Northern Hemisphere case, the jet-stream winds in (c) are from the west (i.e., toward the reader). In Fig. b, height contours are light blue (dashed and thin solid), and isobars are black. You can superimpose copies of these three figures to see the relationship between the temperature field, mass field (i.e., pressures), and wind field.

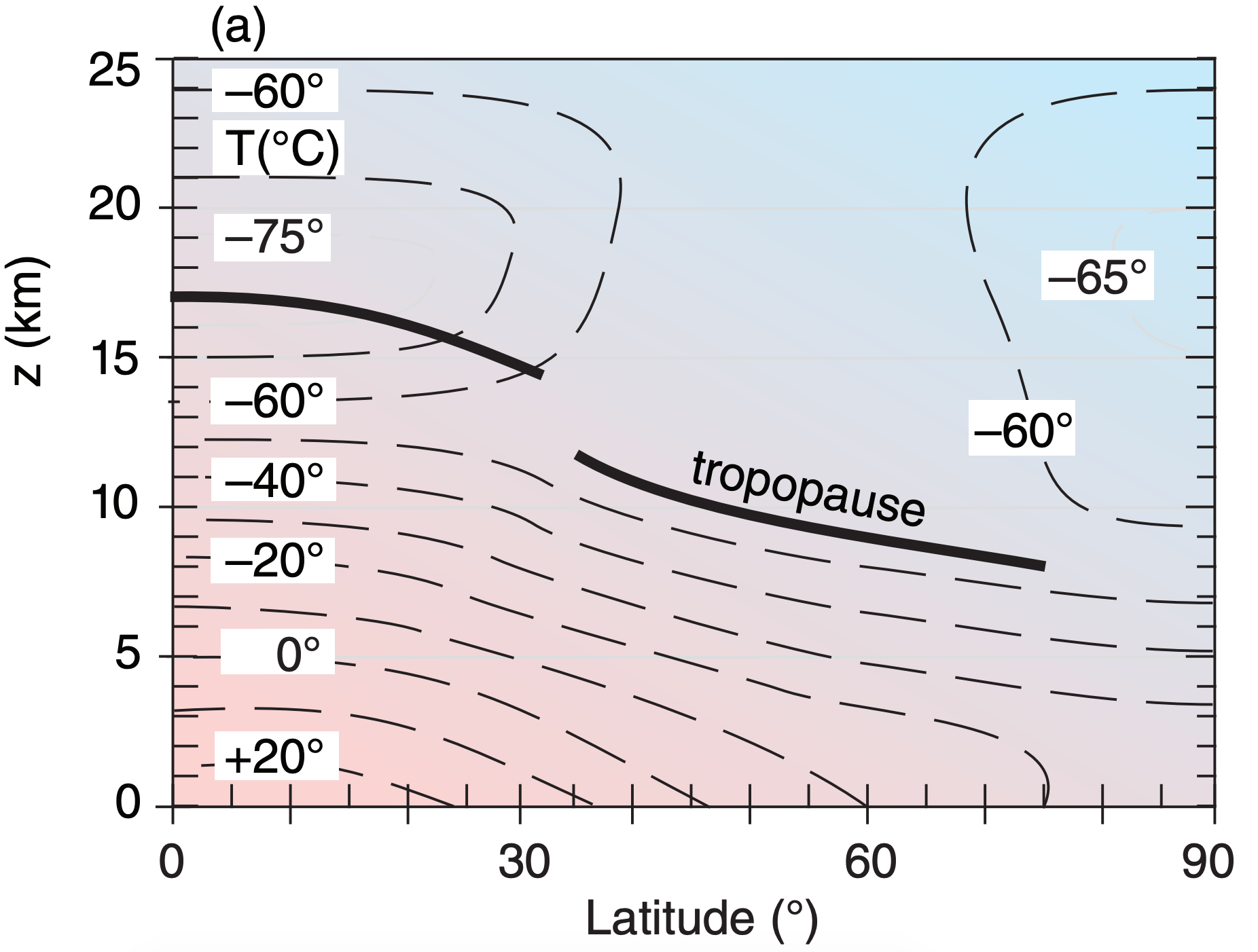
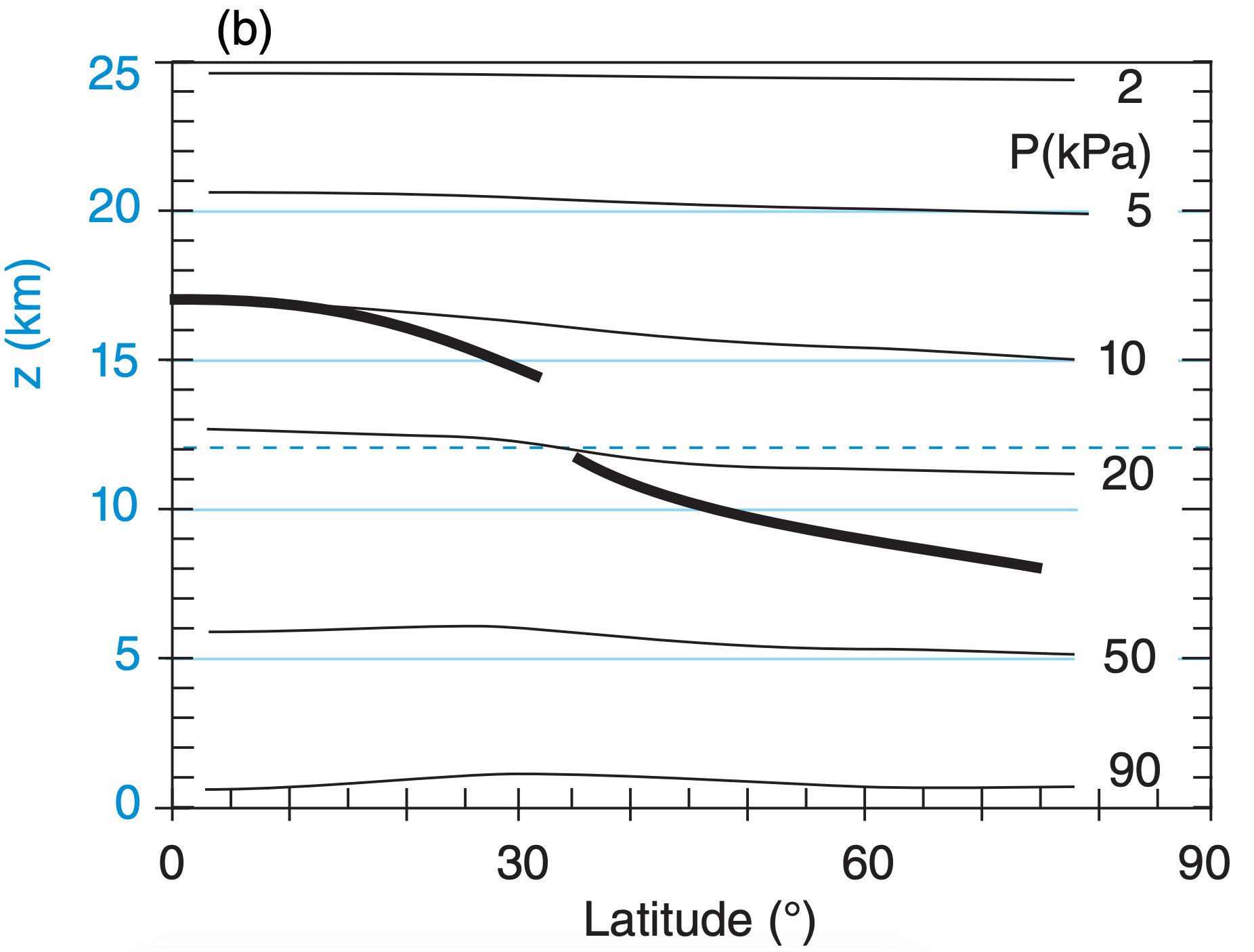
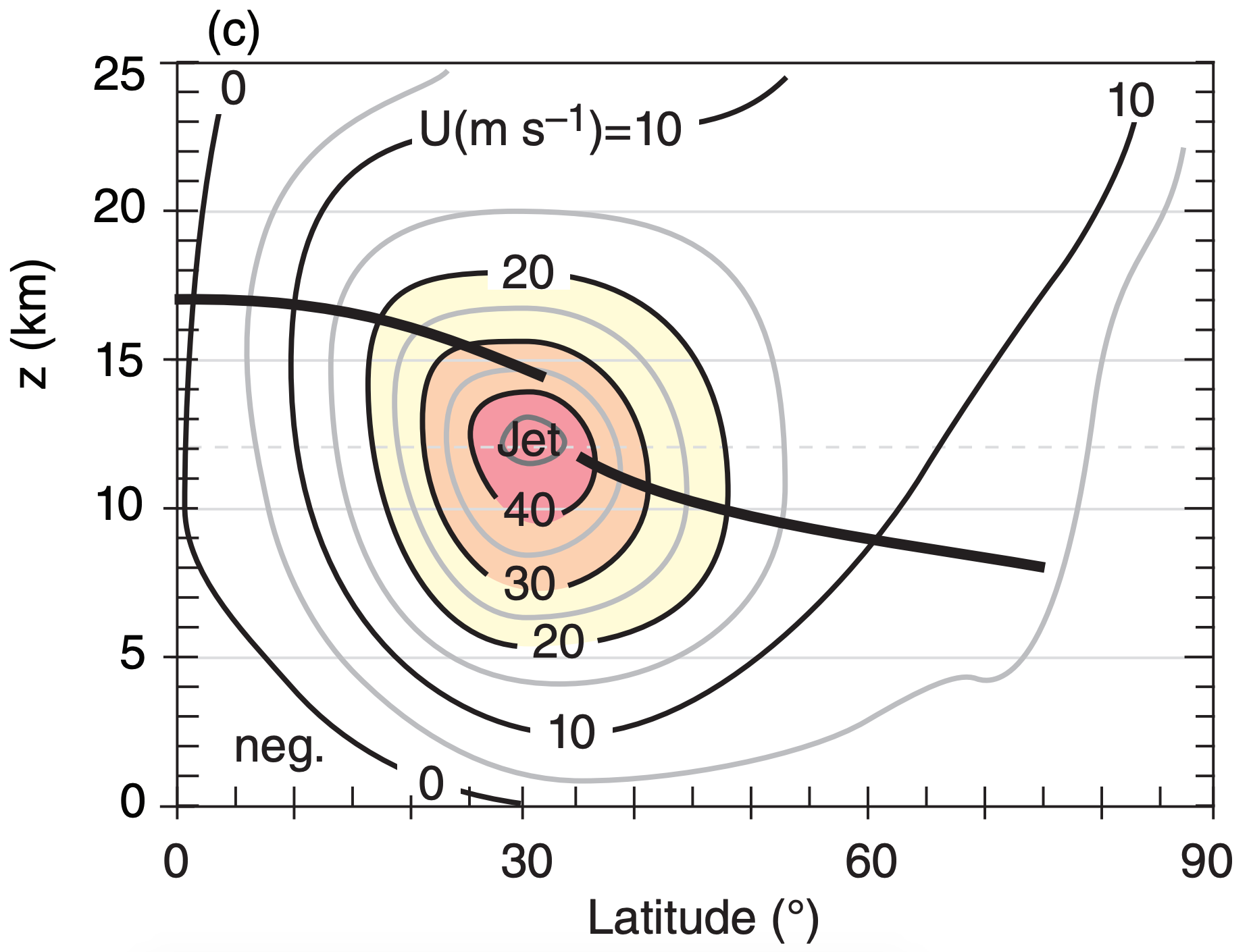
First, consider how temperature varies with height and latitude (Fig. 11.37a). At any altitude in the troposphere you will find a horizontal temperature gradient between colder poles and warmer equator. According to the hypsometric relationship, the thickness between two isobaric surfaces is smaller in the colder (polar) air and greater in the warmer (equatorial) air (Fig. 11.37b). Hence, isobaric surfaces tilt in the horizontal, which drives a geostrophic wind (Fig. 11.37c).

The greatest tilt is near 30° latitude at the tropopause, and the associated pressure gradient drives the fastest winds (jet-stream core) there, as expected due to the thermal wind. Because the isobars cross the isotherms (and isobars also cross the isopycnics — lines of equal density), the atmosphere is said to be baroclinic. It is this baroclinicity associated with the meridional temperature gradient that creates the west winds of the jet stream.

Notice that the troposphere is deeper near the equator than near the poles. Thus, the typical lapse rate in the troposphere, applied over the greater depth, causes colder temperatures at the tropopause over the equator than over the poles (Fig. 11.37a). In the stratosphere above the equatorial tropopause, the air is initially isothermal, but at higher altitudes the air gets warmer. Meanwhile, further north in the stratosphere, such as at latitude 60°, the air is isothermal over a very large depth. Thus, the meridional temperature gradient reverses in the bottom of the stratosphere, with warmer air over 60° latitude and colder equatorial air.

The associated north-south thickness changes between isobaric surfaces cause the meridional pressure gradient to decrease, which you can see in Fig. 11.37b as reductions in slopes of the isobars. The reduced pressure gradient in the lower stratosphere causes wind speeds to decrease with increasing altitude (Fig. 11.37c), leaving the jet max at the tropopause. Near the jet core is a region where the tropopause has a break or a fold, as is covered in the Fronts and Extratropical Cyclone chapters.

You can apply the concepts described above to the toy model of eq. (11.1) and Fig. 11.8. Using that model with eqs. (11.2, 11.4 & 11.13) gives

\(\ \begin{align} U_{j e t} \approx \frac{|g| \cdot c \cdot b_{1}}{2 \Omega \cdot T_{v}} \cdot z \cdot\left(1-\frac{z}{2 \cdot z_{T}}\right) \cdot \cos ^{2}(\phi) \cdot \sin ^{2}(\phi)\tag{11.17}\end{align}\)

where ϕ is latitude, |g| = 9.8 m s^–2, U_g has been relabeled as U_jet, T_v is average absolute virtual temperature, b₁ ≈ 40 K, c = 1.18x10^–3 km^–1, z_T ≈ 11 km is average depth of the troposphere, and assuming U_jet = 0 at z = 0. The factor 2·Ω = 1.458x10^–4 s^–1 comes from the Coriolis-parameter definition f_c = 2·Ω·sinϕ.

The thermal-wind relationship tells us that the meridional variation of temperature between the cold poles and warm equator will drive westerly jet-stream winds in both hemispheres. Namely, the opposite Coriolis-parameter signs in the two hemispheres are canceled by the opposite meridional temperature-gradient signs, yielding positive values for U_g in the two hemispheres.

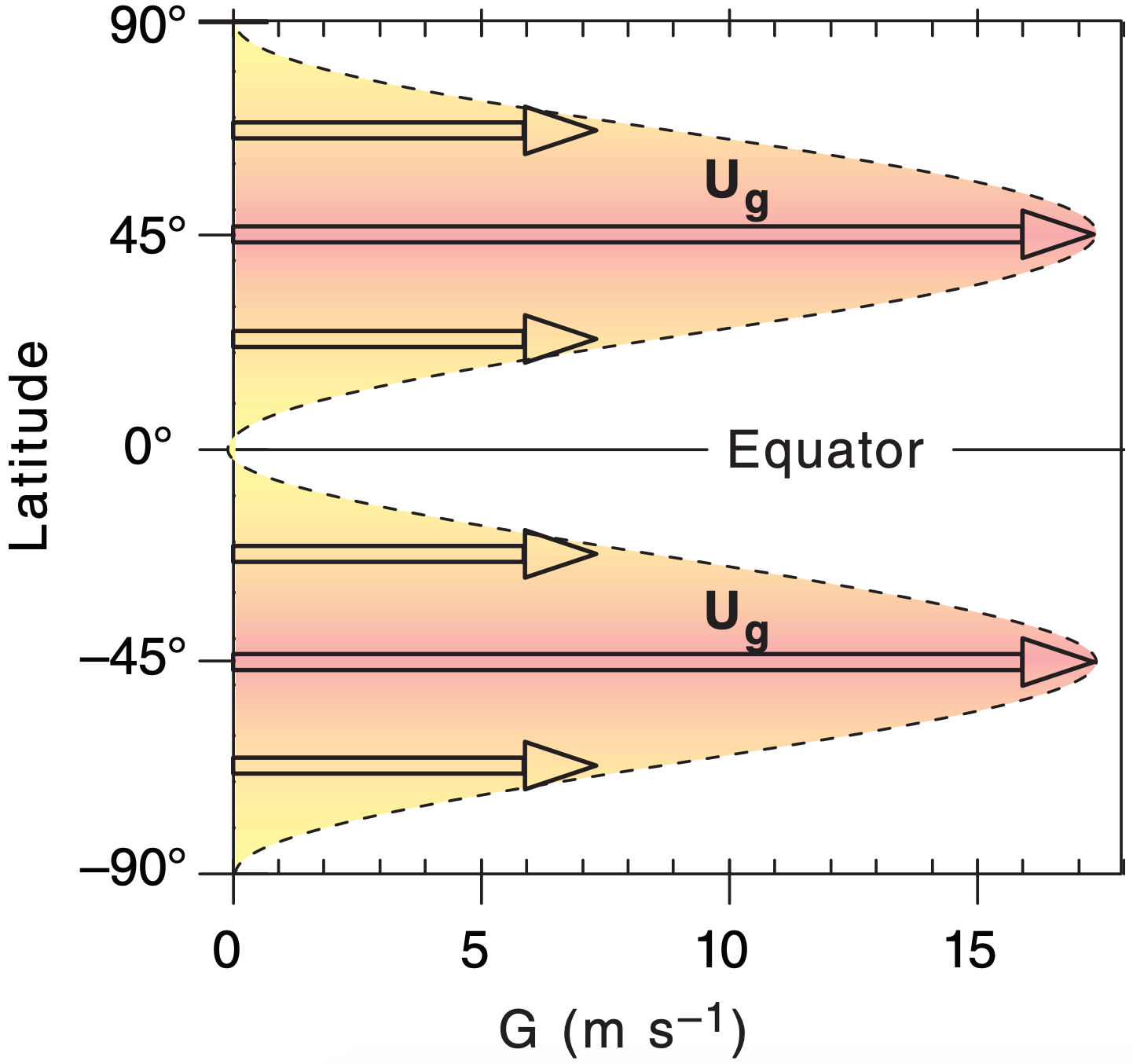
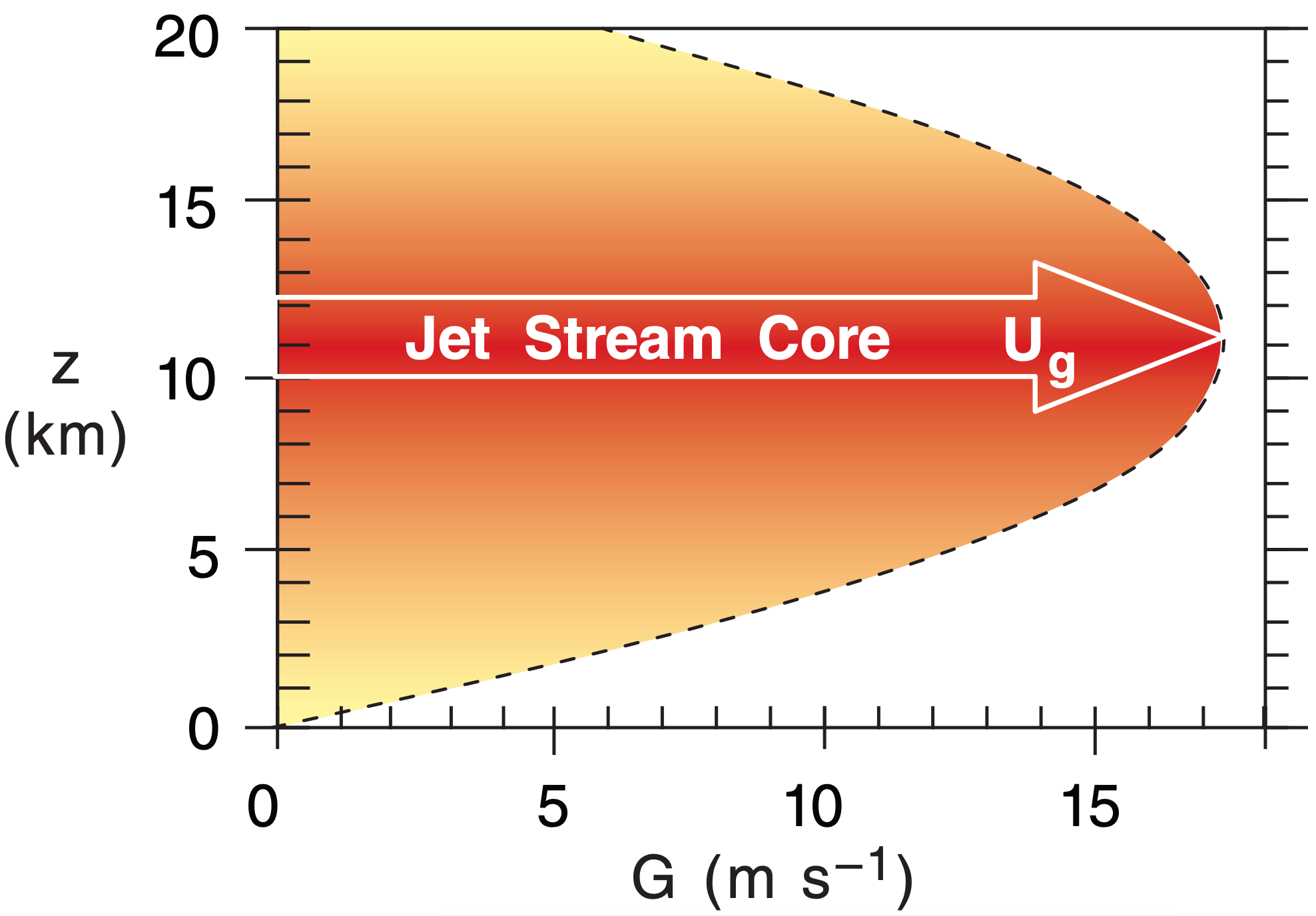
Although Fig. 11.8 indicates the largest meridional temperature gradients are at roughly 50° latitude (north & south) in our toy model, the meridional variation of the Coriolis parameter conspires to make the fastest jet-stream winds at 45° latitude (north & south) according to eq. (11.17). Solving eq. (11.27) for a tropopause height of z_T = 11 km with an average virtual temperature of –20°C in the troposphere gives peak jet-stream wind speeds (Figs. 11.38 & 11.39) of about 17.25 m s^–1.

While our simple toy model is insightful because it mimics the main features of the global circulation and allows an analytical solution that you can solve on a spreadsheet, it is too simple. Compared to Fig. 11.37, the toy jet-stream speeds are too slow, are located too far poleward, and don’t give fast-enough winds near the ground. Also, actual locations in both hemispheres shift a bit to the (north, south) in northern hemisphere (summer, winter).

Figure 11.38 Idealized profile of 11 km altitude jet-stream winds vs. latitude.

Figure 11.39 Idealized profile of 45°N latitude jet-stream winds vs. altitude.

Sample Application

Use the toy-model temperature eqs. (11.1 & 11.4) to estimate the speed of the geostrophic wind for latitude 60° at the top of the troposphere. Assume T_v = –5°C.

Find the Answer

Given: ϕ = 60°, Tv = 268 K, z = z_T.

Find: U_jet = ? m s^–1.

From Fig. 11.39 estimate troposphere top zT ≈ 9 km. Apply eq. (11.17), which already incorporates toy model eq. (11.4).

\(U_{j e t} \approx \frac{\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right) \cdot\left(1.18 \times 10^{-3} \mathrm{km}^{-1}\right) \cdot(40 \mathrm{K})}{\left(1.458 \times 10^{-4} \mathrm{s}^{-1}\right) \cdot(268 \mathrm{K})} \cdot
(9 \mathrm{km}) \cdot(1-(1 / 2)) \cdot \cos ^{2}\left(60^{\circ}\right) \cdot \sin ^{2}\left(60^{\circ}\right)\)

= 10. m s^–1

Check: Physics & units are reasonable.

Exposition: Agrees with Fig. 11.37c. During winter the poles are colder relative to the equator, driving faster jet-stream winds than summer. Peak winds in the jet core can reach 100 m s^–1 , although 3-month-average speeds are typically 40 m s^–1.

11.8.2. Angular Momentum & Subtropical Jet

Angular momentum can influence the subtropical jet, and is defined as mass times velocity times radius of curvature. Suppose that initially there is air moving at some zonal velocity U_s relative to the Earth’s surface at some initial (source) latitude ϕ_s. Because the Earth is rotating, the Earth’s surface at the source latitude is moving toward the east at velocity U_Es. Thus, the total eastward speed of the air parcel relative to the Earth’s axis is (U_s + U_Es).

Figure 11.40 Geometry for angular-momentum calculations affecting an air parcel that moves toward the north.

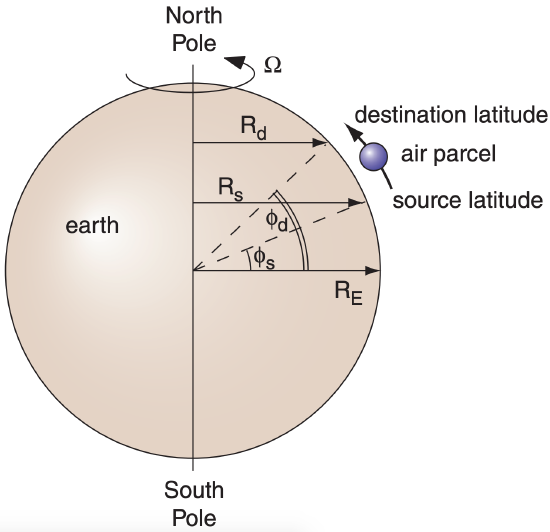
As sketched in Fig. 11.40, suppose some disturbance such as a meandering jet stream moves the air to some other (destination) latitude ϕ_d, assuming that no other forces are applied. Conservation of angular momentum requires:

\(\ \begin{align} m \cdot\left(U_{s}+U_{E s}\right) \cdot R_{s}=m \cdot\left(U_{d}+U_{E d}\right) \cdot R_{d}\tag{11.18}\end{align}\)

where U_d represents the new zonal air velocity relative to the Earth’s surface at the destination latitude, U_Ed is the tangential velocity of the Earth’s surface at the destination, and m is air mass.

For latitude ϕ at either the source or destination, the radius is R_s or R_d = R_E·cos(ϕ), where average Earth radius is R_E = 6371 km. Similarly, tangential velocities at either the source or destination are Us or U_d = Ω·R_ϕ = Ω·R_E·cos(ϕ), for an Earth angular velocity of Ω = 0.729x10^–4 s^–1.

Solving these equations for the destination air velocity Ud relative to Earth’s surface gives:

\(\ \begin{align} U_{d}=\left[\Omega \cdot R_{E} \cdot \cos \left(\phi_{s}\right)+U_{s}\right] \cdot \frac{\cos \left(\phi_{s}\right)}{\cos \left(\phi_{d}\right)}-\Omega \cdot R_{E} \cdot \cos \left(\phi_{d}\right)\tag{11.19}\end{align}\)

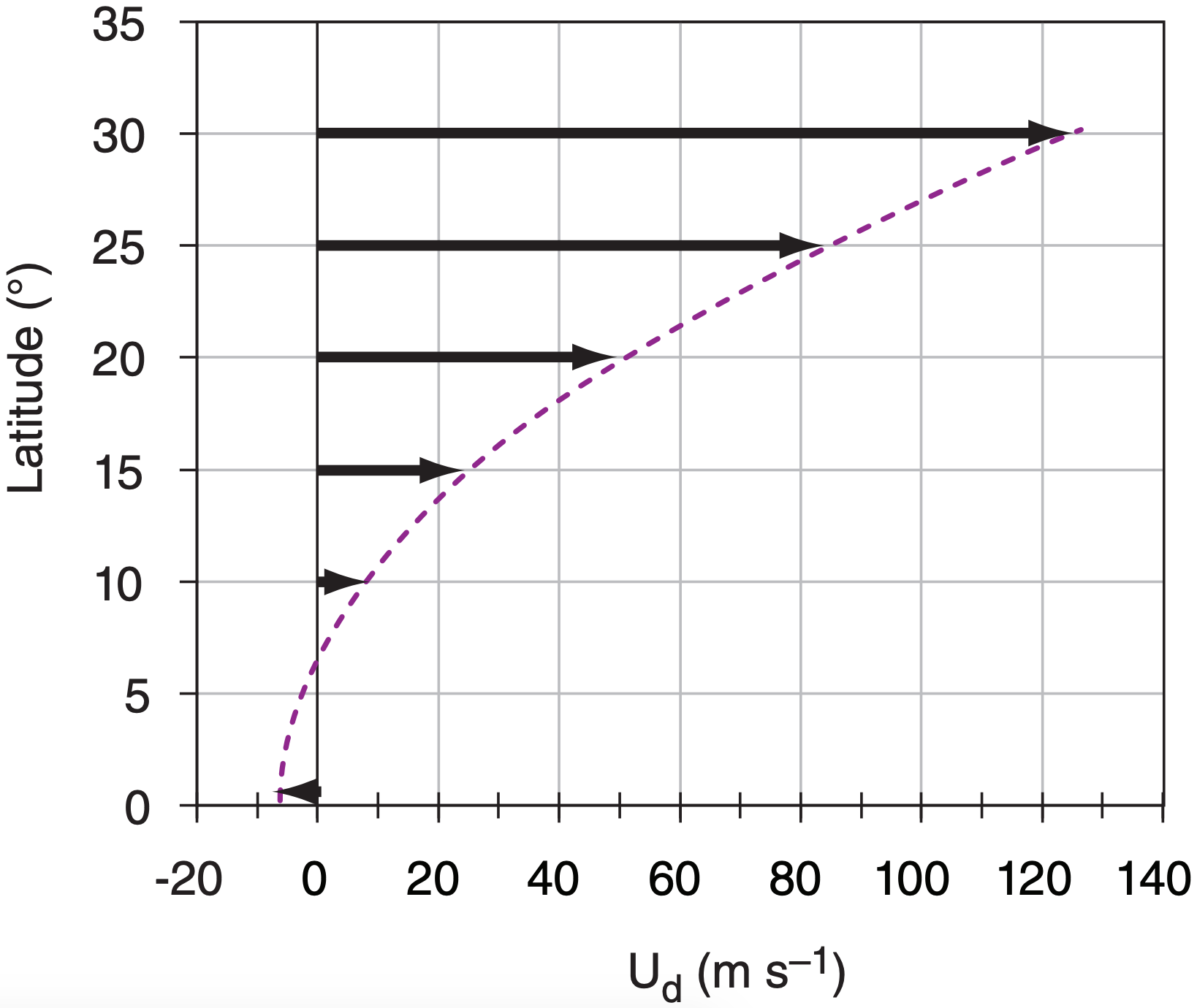
As we already discussed, winds at the top of the Hadley cell diverge away from the equator, but cannot move beyond 30° latitude because Coriolis force turns the wind. When we use eq. (11.19) to predict the zonal wind speed for typical trade-wind air that starts at the equator with U_s = –7 m s^–1 and ends at 30° latitude, we find unrealistically large wind speeds (125 m s^–1) for the subtropical jet (Fig. 11.41). Actual typical wind speeds in the subtropical jet are of order 40 to 80 m s^–1 in the winter hemisphere, and slower in the summer hemisphere.

The discrepancy is because in the real atmosphere there is no conservation of angular momentum due to forces acting on the air. Coriolis force turns the wind, causing air to accumulate and create a pressure-gradient force to oppose poleward motion in the Hadley cell. Drag due to turbulence slows the wind a small amount. Also, the jet streams meander north and south, which helps to transport slow angular momentum southward and fast angular momentum northward. Namely, these meanders or synoptic-scale eddies cause mixing of zonal momentum.

Next, the concept of vorticity is discussed, which will be useful for explaining how troughs and ridges develop in the jet stream. Then, we will introduce a way to quantify circulation, to help understand the global wind patterns.

Figure 11.41 Computed zonal wind speed U_d at various destination latitudes for typical trade-wind air that starts at the equator with U_s = –7 m s^–1, for the unrealistic case of conservation of angular momentum. Actual zonal winds are not this fast at 30° latitude.

Sample Application

For air starting at the equatorial tropopause, what would be its zonal velocity at 20°N if angular momentum were conserved?

Find the Answer

Given: ϕ_d = 20°N, ϕ_s = 0°, Ω·R_E = 463 m s^–1

Find: U_d = ? m s^–1

Assume: no turbulence; U_s = –7 m s^–1 easterlies.

Use eq. (11.19): U_d =

\(\left[(463 \mathrm{m} / \mathrm{s}) \cos \left(0^{\circ}\right)+U_{s}\right] \frac{\cos \left(0^{\circ}\right)}{\cos \left(20^{\circ}\right)}-(463 \mathrm{m} / \mathrm{s}) \cos \left(20^{\circ}\right)\)

U_d = = 50.2 m s^–1

Check: Physics & units are reasonable. Agrees with Fig. 11.41

Exposition: Actual winds are usually slower, because of turbulent drag and other forces..