11.7: Explaining the General Circulation
- Page ID
- 10204
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)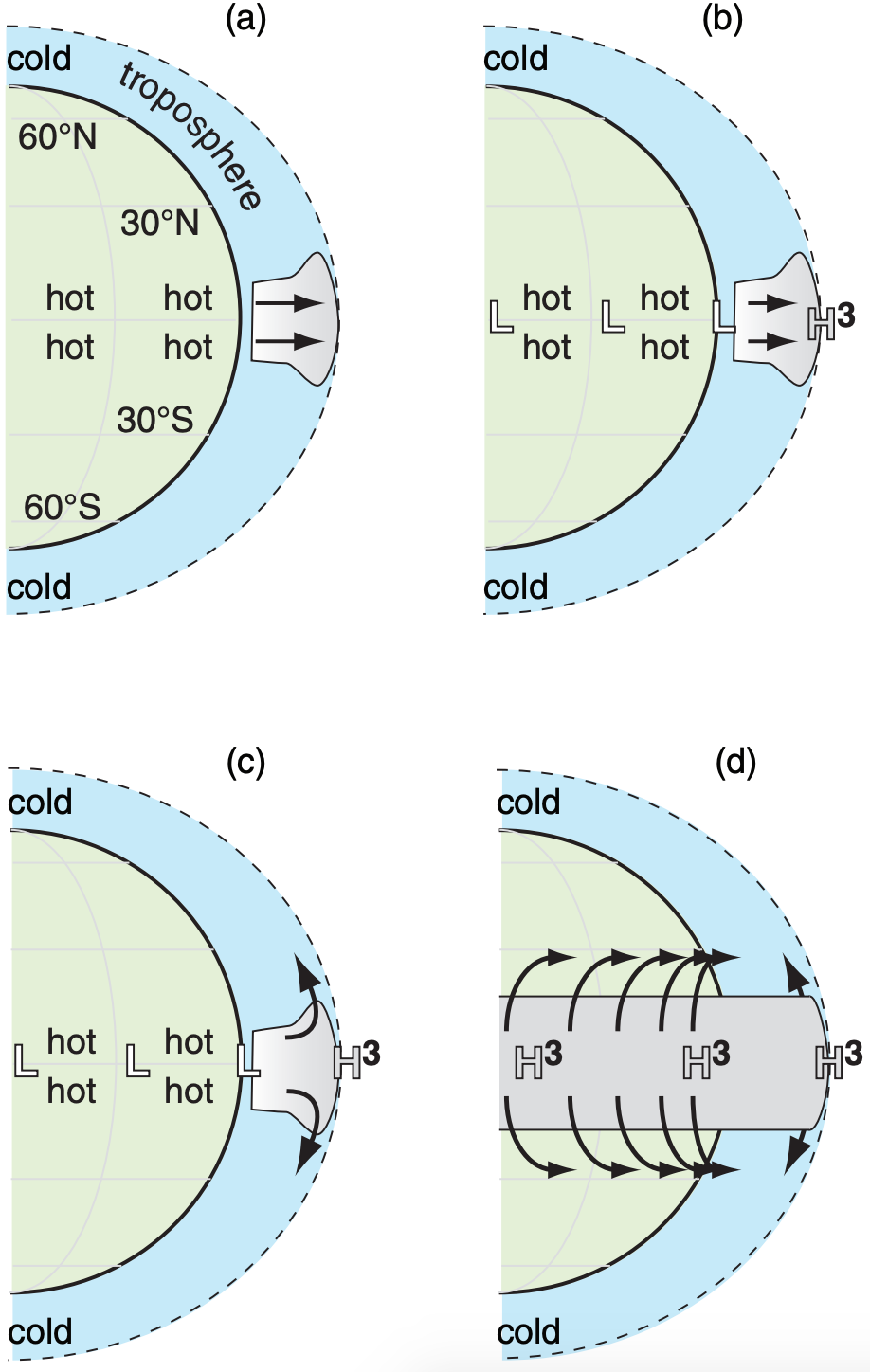
11.7.1. Low Latitudes
Differential heating of the Earth’s surface warms the tropics and cools the poles (Fig. 11.26a). The warm air near the equator can hold large amounts of water vapor evaporated from the oceans. Buoyancy force causes the hot humid air to rise over the equator. As the air rises, it cools and water vapor condenses, causing a belt of thick thunderstorm clouds around the equator (Fig. 11.26a) with heavy tropical precipitation.
The buoyantly forced vertical motion removes air molecules from the lower troposphere in the tropics, and deposits the air near the top of the troposphere. The result is a pressure couplet (Fig. 11.26b) of very high perturbation pressure p’ (indicated with HHH or H3 on the figures) near the tropopause, and low perturbation pressure (L in the figures) at the surface.
The belt of tropical high pressure near the tropopause forces air to diverge horizontally, forcing some air into the Northern Hemisphere and some into the Southern (Fig. 11.26c). With no Coriolis force at the equator, these winds are driven directly away from the high-pressure belt.
As these high-altitude winds move away from the equator, they are increasingly affected by Coriolis force (Fig. 11.26d). This causes winds moving into the Northern Hemisphere to turn to their right, and those moving into the Southern Hemisphere to turn to their left. Winds in both hemispheres accelerate.
But as the winds move further and further away from the equator, they are turned more and more to the east, creating the subtropical jet (Fig. 11.26e) at about 30° latitude. Coriolis force prevents these upper-level winds from getting further away from the equator than about 30° latitude (north and south), so the air accumulates and the pressure increases in those belts.
When simulations of the general circulation impose a larger Coriolis force (as if the Earth spun faster), the convergence bands occur closer to the equator. This effect is indeed found in the atmospheres of Jupiter and Saturn, as is evident by motions in their banded structures. For weaker Coriolis force, the convergence is closer to the poles. But for our Earth, the air converges at 30° latitude.
This pressure perturbation p’ is labeled as HH or H2 in Fig. 11.26e, to show that it is a positive pressure perturbation, but not as strong as the H3 perturbation over the equator. Namely, the horizontal pressure gradient between H3 and H2 drives the upperlevel winds to diverge away from the equator.
CAUTION: Whenever you find that a model has high sensitivity (i.e., the output result varies by large magnitude for small changes in the input parameter), you should be especially wary of the results. Small errors in the parameter could cause large errors in the result. Also, if the real atmosphere does not share the same sensitivity, then this is a clue that the model is poorly designed, and perhaps a better model should be considered.
Models are used frequently in meteorology — for example: numerical weather prediction models (Chapter 20) or climate-change models (Chapter 21). Most researchers who utilize models will perform careful sensitivity studies (i.e., compute the output results for a wide range of parameter values) to help them gauge the potential weaknesses of the model.
The excess air accumulated at 30° latitudes cannot go up into the stratosphere in the face of very strong static stability there. The air cannot go further poleward because of Coriolis force. And the air cannot move equatorward in the face of the strong upper-level winds leaving the equator. The only remaining path is downward at 30° latitude (Fig. 11.26f) as a nonhydrostatic flow. As air accumulates near the ground, it causes a high-pressure perturbation there — the belt of subtropical highs labeled with H.
The descending air at 30° latitude warms dryadiabatically, and does not contain much moisture because it was squeezed out earlier in the thunderstorm updrafts. These are the latitudes of the subtropical deserts (Fig. 11.26h), and the source of hot airmasses near the surface.
Finally, the horizontal pressure gradient between the surface subtropical highs near 30° latitude and the equatorial lows near 0° latitude drives the surface winds toward the equator. Coriolis force turns these winds toward the west in both hemispheres (Fig. 11.26g), resulting in the easterly trade winds (winds from the east) that converge at the ITCZ.
The total vertical circulation in the tropics and subtropics we recognize as the Hadley Cell (labeled h.c. in Fig. 11.26f). This vertical circulation (a thermally-direct circulation) is so vigorous in its vertical mixing and heat transport that it creates a deeper troposphere in the tropics than elsewhere (Fig. 11.4). Also, the vigorous circulation spreads and horizontally mixes the radiatively warmed air somewhat uniformly between ±30° latitude, as sketched by the flattened temperature curve in Fig. 11.8a.
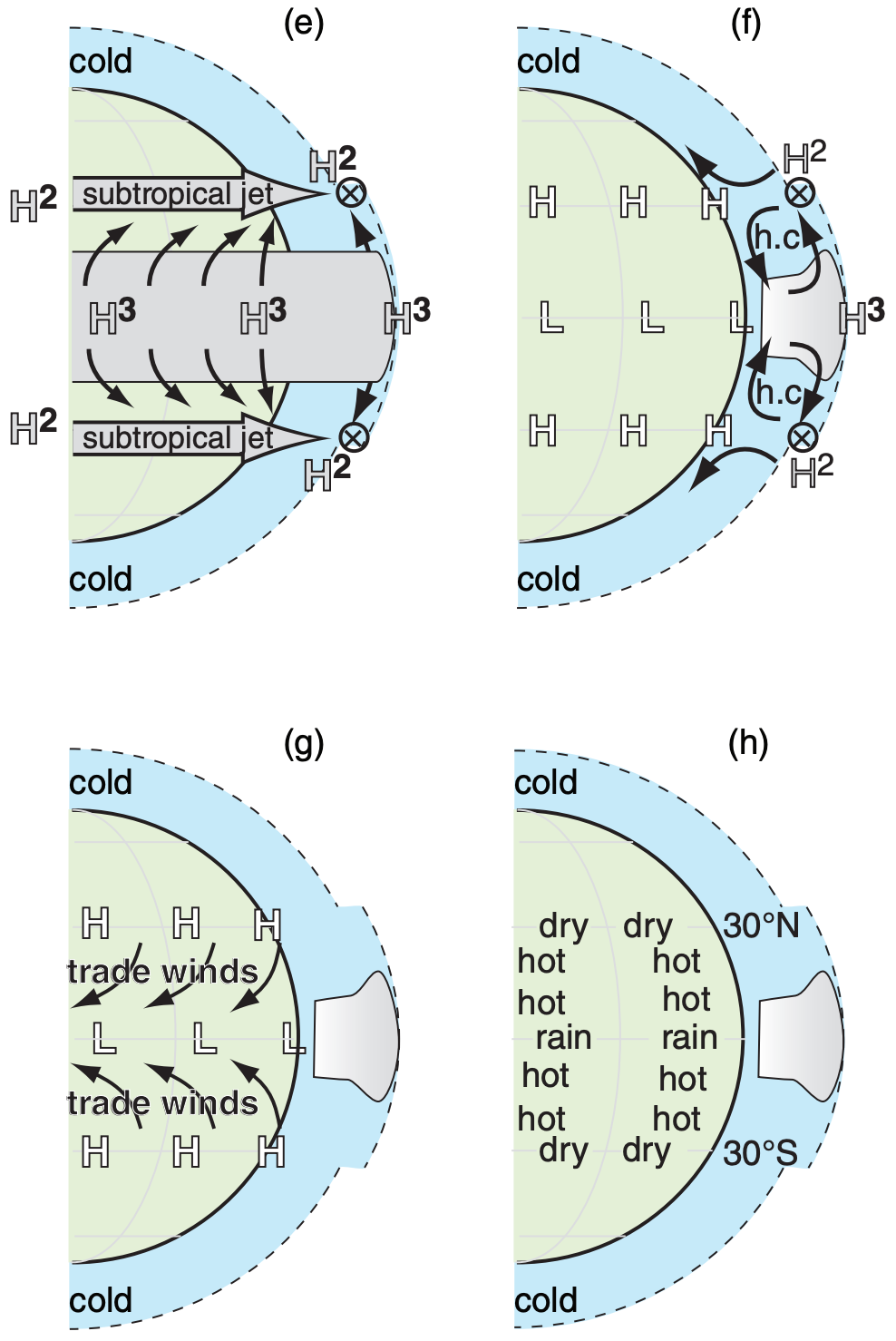
 Descending air in the subtropical arm of the Hadley circulation is hot and dry. Air near the tropical sea surface is relatively cool and humid. Between these layers is a strong temperature inversion called the trade inversion or passat inversion. This statically stable layer (between the dashed lines in the Figure) creates a lid to the tropical convection below it. The inversion base is lowest (order of 500 m) in the subtropics, and is highest (order of 2,500 m) near the ITCZ. Fair-weather cumulus clouds (trade cumuli) between the lifting condensation level (LCL) and the trade inversion are shallowest in the subtropics and deeper closer to the ITCZ.
Descending air in the subtropical arm of the Hadley circulation is hot and dry. Air near the tropical sea surface is relatively cool and humid. Between these layers is a strong temperature inversion called the trade inversion or passat inversion. This statically stable layer (between the dashed lines in the Figure) creates a lid to the tropical convection below it. The inversion base is lowest (order of 500 m) in the subtropics, and is highest (order of 2,500 m) near the ITCZ. Fair-weather cumulus clouds (trade cumuli) between the lifting condensation level (LCL) and the trade inversion are shallowest in the subtropics and deeper closer to the ITCZ.
By capping the humid air below it, the trade inversion allows a latent-heat fuel supply to build up, which can be released in hurricanes and ITCZ thunderstorms.
11.7.2. High Latitudes
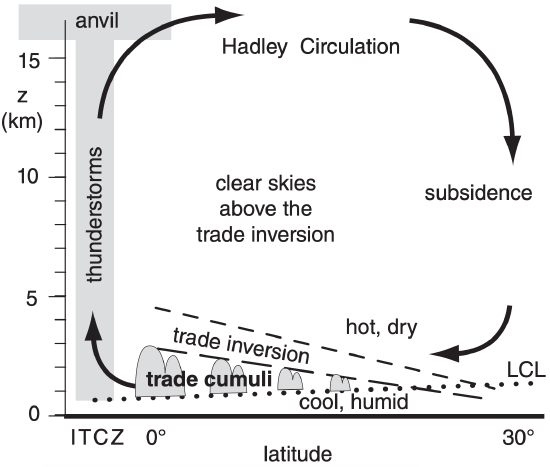
As sketched in Fig. 11.8a, air temperature is very cold at the poles, and is cool at 60° latitude. The temperature difference between 60° and 90° latitudes creates opposite north-south pressure gradients and winds at the top and bottom of the troposphere, due to the thermal circulation effect (Fig. 11.17). A vertical cross section of this thermal circulation (Fig. 11.27a) shows a weak polar cell. Air generally rises near 60°N and descends near the pole.
At the poles are surface high-pressure centers, and at 60° latitudes are belts of subpolar lows at the surface. This horizontal pressure gradient drives equatorward winds, which are turned toward the west in both hemispheres due to Coriolis force (Fig. 11.27b). Namely, the winds become geostrophic, and are known as polar easterlies.
At the top of the shallow (6 to 8 km thick) troposphere are poleward winds that are turned toward the east by Coriolis force. These result in an upperlevel westerly flow that circulates around the upperlevel polar low (Fig. 11.3b).
11.7.3. Mid-latitudes
Recall that the Hadley cell is unable to mix heat beyond about ±30° latitude. This leaves a very strong meridional temperature gradient in mid-latitudes (Fig. 11.8) throughout the depth of the troposphere. Namely, the temperature change between the equator (0°) and the poles (90°) has been compressed to a latitude band of about 30 to 60° in each hemisphere.
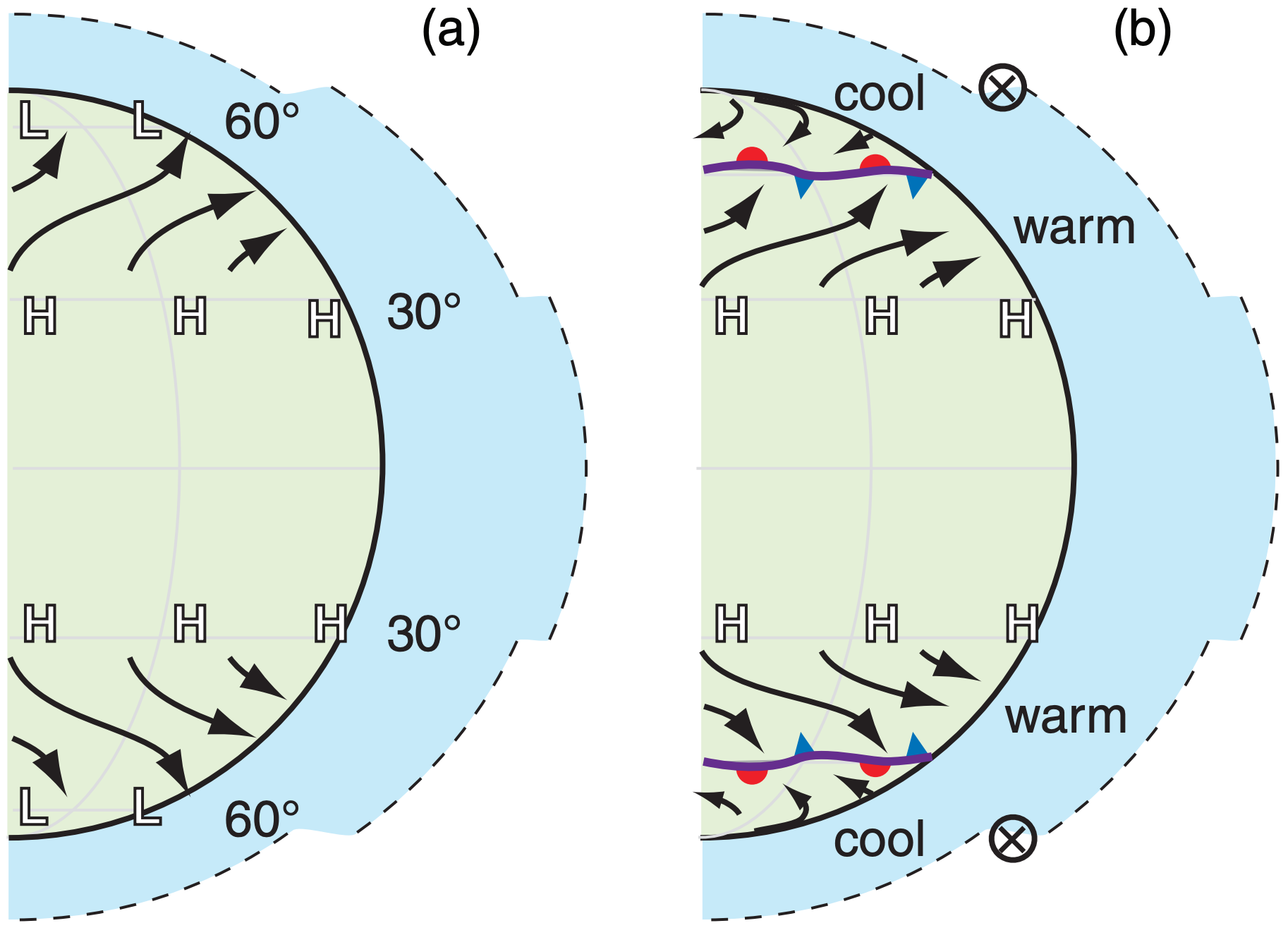
Between the subtropical high-pressure belt near 30° latitude and the subpolar low-pressure belt near 60° latitude is a weak meridional pressure gradient near the Earth’s surface. This climatological-average pressure gradient drives weak boundary-layer winds from the west in both hemispheres (Fig. 11.28a), while the drag of the air against the surface causes the wind to turn slightly toward low pressure.
Near the subpolar belt of low pressure is a region of surface-air convergence, with easterly winds from the poles meeting westerly winds from mid-latitudes. The boundary between the warm subtropical air and the cool polar air at the Earth’s surface is called the polar front (Fig. 11.28b) — a region of even stronger horizontal temperature gradient.
Recall from the hypsometric equation in Chapter 1 that the height difference (i.e., the thickness) between two isobaric surfaces increases with increasing temperature. As a result of the meridional temperature gradient, isobaric surfaces near the top of the troposphere in mid-latitudes are much more steeply sloped than near the ground (Figs. 11.29 & 11.32). This is related to the thermal-wind effect.

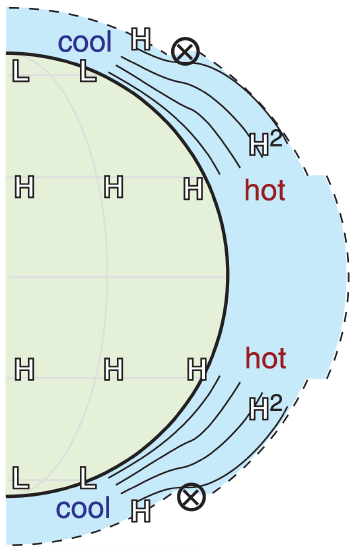

In the Northern Hemisphere this effect is greatest in winter (Fig. 11.32), because there is the greatest temperature contrast between pole and equator. In the Southern Hemisphere, the cold Antarctic continent maintains a strong meridional temperature contrast all year.
Larger pressure gradients at higher altitudes drive stronger winds. The core of fastest westerly winds near the tropopause (where the pressure-gradient is strongest) is called the polarjet stream, and is also discussed in more detail later in this chapter. Thus, the climatological average winds throughout the troposphere at mid-latitudes are from the west (Fig. 11.30a) in both hemispheres.
Although the climatological average polar-jetstream winds are straight from west to east (as in Fig. 11.30a), the actual flow on any single day is unstable. Two factors cause this instability: the variation of Coriolis parameter with latitude (an effect that leads to barotropic instability), and the increase in static stability toward the poles (an effect that leads to baroclinic instability). Both of these instabilities are discussed in more detail later.
Air flow over a surface heterogeneity such as a mountain range can cause the initial meridional deviation of the jet stream. Once triggered, the jet stream continues to meander or oscillate north-south as it generally blows from the west (Fig. 11.30b). The meanders that form in this flow are called Rossby waves. Regions near the tropopause where the jet stream meanders equatorward are called troughs, because the lower pressure on the north side of the jet stream is brought equatorward there. Poleward meanders of the jet stream are called ridges, where higher pressure extends poleward. The locations of Rossby-wave troughs and ridges usually propagate toward the east with time, as will be explained in detail later in this chapter.
Recall that there is a subtropical jet at roughly 30° latitude associated with outflow from the Hadley Cell. Thus, in each hemisphere is a somewhat-steady subtropical jet and a meandering polar jet (Fig. 11.30b). Both of these jets are strongest in the winter hemisphere, where there is the greatest temperature gradient between cold poles and hot equator.
Troughs and ridges in the jet stream are crucial in creating and destroying cyclones and anticyclones near the Earth’s surface. Namely, they cause the extremely large weather variability that is normal for mid-latitudes. The field of synoptic meteorology comprises the study and forecasting of these variable systems, as discussed in the Airmasses, Fronts, and Extratropical Cyclone chapters.
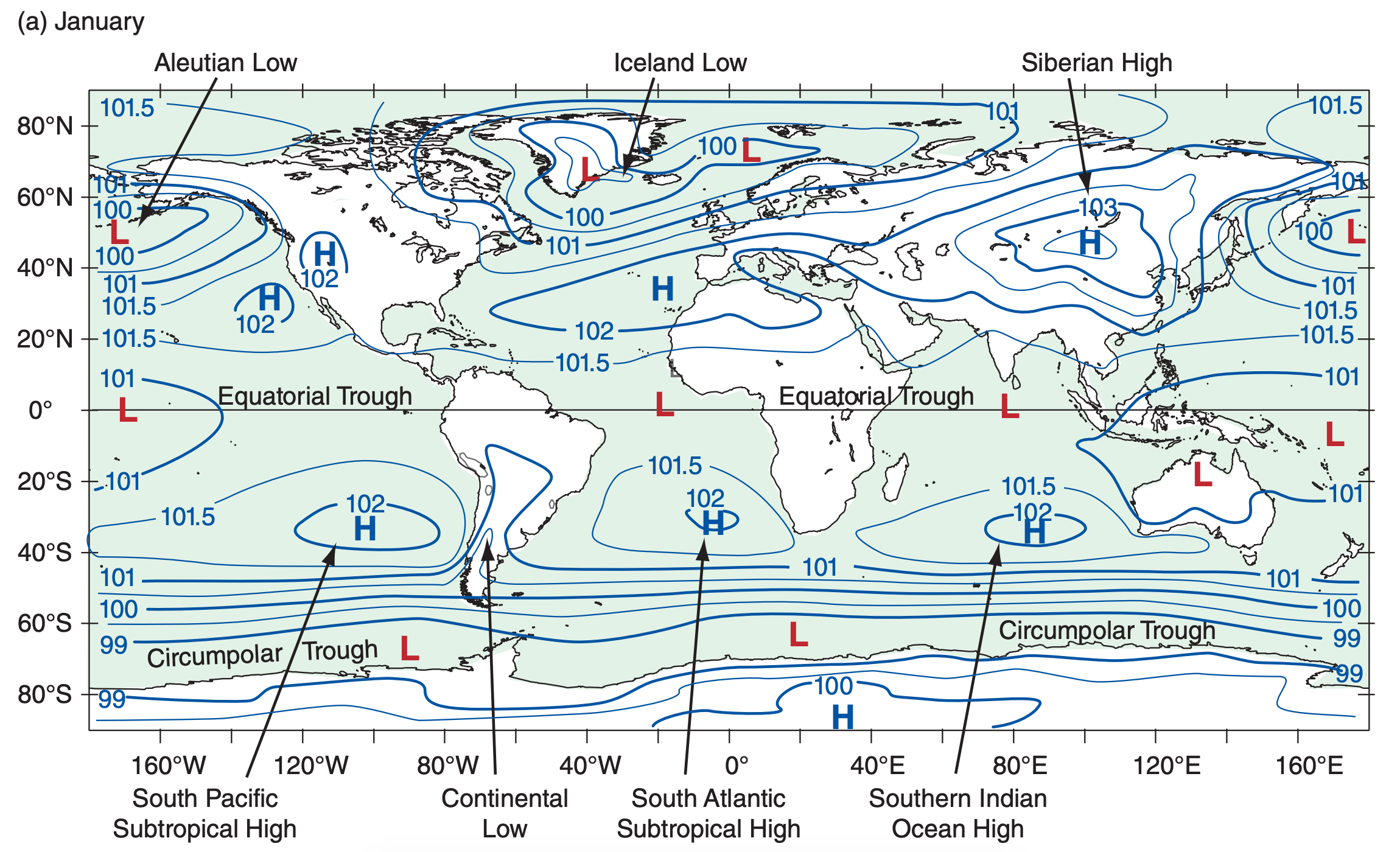
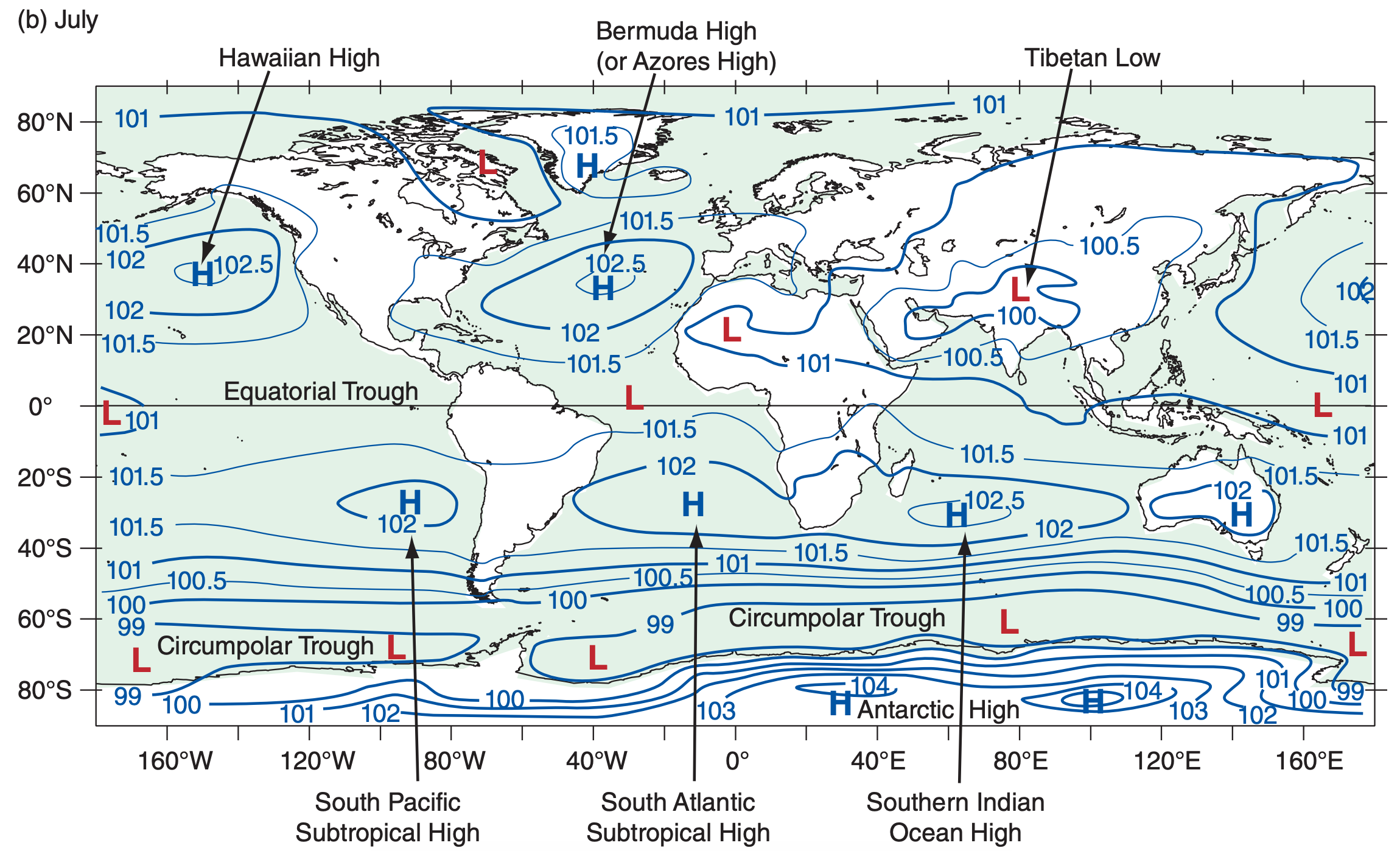
Figs. 11.31 and 11.32 show actual global pressure patterns at the bottom and top of the troposphere. The next section explains why the patterns over the oceans and continents differ.

11.7.4. Monsoon
Recall from the Heat Budgets chapter that the temperature change of an object depends on the mass of material being heated or cooled, and on the material’s specific heat. If you put the same amount of heat into objects of similar material but differing mass, the smaller masses will warm the most.
Rocks and soil on continents are opaque to sunlight, and are good insulators of heat. Thus, sunlight directly striking the land surface warms only a very thin top layer (mm) of molecules, causing this thin layer to get quite warm. Similarly, longwave (infrared) radiative heat loss at night causes the very thin top layer to become very cold. Namely, there is a large diurnal (daily) temperature contrast. Also, because there are more daylight hours in summer and more nighttime hours in winter, continental land surfaces tend to become hot in summer and cold in winter.
Water in the oceans is partially transparent and sometimes turbulent, allowing sunlight to be absorbed and spread over a thick layer (meters to tens of meters) of molecules. Also, water has a large specific heat (see the Heat Budgets chapter), hence a large input of heat causes only a small temperature change. Thus, ocean surfaces have very small diurnal temperature changes, and have only a medium amount of seasonal temperature changes.
The net result is that during summer, continents warm faster than the oceans. During winter, continents cool faster than the oceans.
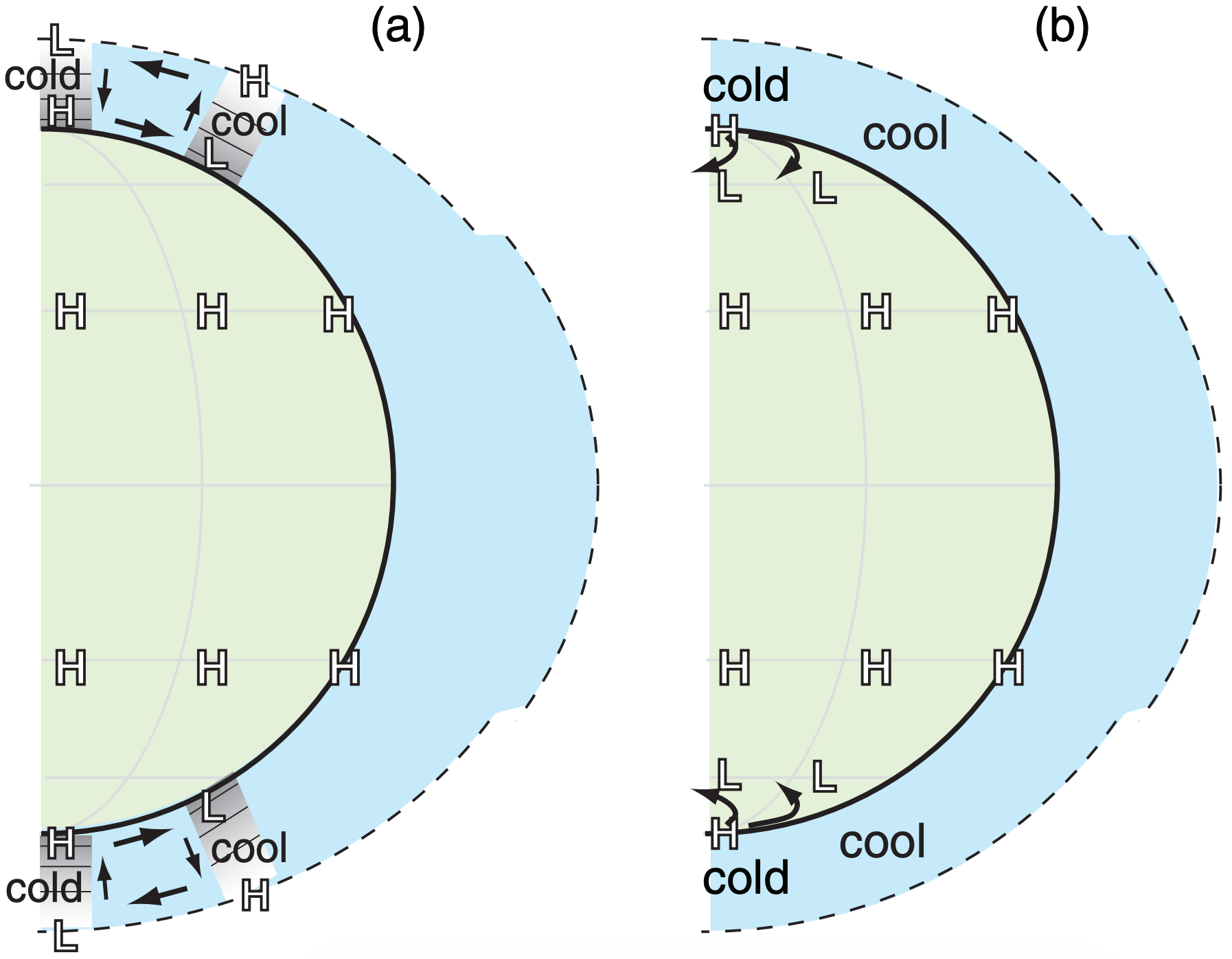
Consider a cold region next to a warm region. Over the cold surface, the near-surface air cools and develops a high-pressure center with anticyclonically rotating winds, as explained by the thermal circulation sketched in Fig. 11.17. Over warm surfaces, the thermal circulation causes near-surface air to warm and develop a low-pressure center with cyclonic winds. As already mentioned, this is called a thermal low.
Combining the effects from the previous two paragraphs with the strong tendency of the winds to become geostrophic (or gradient) yields the nearsurface monsoonal flows shown in Fig. 11.5. Opposite pressure patterns and circulations would occur near the top of the troposphere. The regions near surface lows tend to have rising air and abundant clouds and rain. Regions near surface highs tend to have dry fair weather with few clouds.
Monsoon circulations occur over every large continent and ocean (Fig. 11.31). Some are given names. Over the Atlantic in summer, winds on the south and west sides of the monsoonal Bermuda High (also called the Azores High) steer Atlantic hurricanes northward as they near North America. Over the North Pacific in summer is the Hawaiian High or Pacific High which provides cool northerly breezes and months of fair weather to the west coast of North America.
The summer low over northern India is called the Tibetan Low. It helps drive strong cross-equatorial flow (Fig. 11.33) that brings the much needed monsoon rains over India. Ghana in West Africa also receives a cross-equatorial monsoon flow.
Winter continental highs such as the Siberian High over Asia are formation locations for cold airmasses. Over the North Atlantic Ocean in winter is the Icelandic Low, with an average circulation on its south side that steers mid-latitude cyclones toward Great Britain and northern Europe. The south side of the winter Aleutian Low over the North Pacific brings strong onshore flow toward the west coast of North America, causing many days of clouds and rain.
The actual mean global circulation is a superposition of the zonally averaged flows and the monsoonal flows (Fig. 11.31). Also, a snapshot or satellite image of the Earth on any given day would likely deviate from the 30-year averages presented here. Other important aspects of the global circulation were not discussed, such as conversion between available potential energy and kinetic energy. Also, monsoons and the whole global circulation are modulated by El Niño / La Niña events and other oscillations, discussed in the Climate chapter.
In the previous sections, we have described characteristics of the global circulation in simple terms, looked at what drives these motions, and explained dynamically why they exist. Some of the phenomena we encountered deserve more complete analysis, including the jet stream, Rossby waves with their troughs and ridges, and some aspects of the ocean currents. The next sections give details about how these phenomena work.


