19.7: Dispersion in Unstable Boundary Layers (Convective Mixed Layers)
- Page ID
- 10859
During conditions of light winds over an underlying warmer surface (PG types A & B), the boundary layer is statically unstable and in a state of free convection. Turbulence consists of thermals of warm air that rise from the surface to the top of the mixed layer. These vigorous updrafts are surrounded by broader areas of weaker downdraft. The presence of such large turbulent structures and their asymmetry cause dispersion behavior that differs from the usual Gaussian plume dispersion.
As smoke is emitted from a point source such as a smoke stack, some of the emissions are by chance emitted into the updrafts of passing thermals, and some into downdrafts. Thus, the smoke appears to loop up and down, as viewed in a snapshot. However, when averaged over many thermals, the smoke disperses in a unique way that can be described deterministically. This description works only if variables are normalized by free-convection scales.
The first step is to get the meteorological conditions such as wind speed, ABL depth, and surface heat flux. These are then used to define the ABL convective scales such as the Deardorff velocity w* (see eq. 19.22 on the next page). Source emission height and downwind receptor distance are then normalized by the convective mixed-layer scales to make dimensionless distance variables.
Next, the dimensionless (normalized) variables are used to calculate the plume centerline height and vertical dispersion distance. These are then used as a first guess in a Gaussian equation for crosswind-integrated concentration distribution, which is a function of height in the ABL. By dividing each distribution by the sum over all distributions, a corrected cross-wind-integrated concentration can be found that has the desirable characteristic of conserving pollutant mass.
Finally, the lateral dispersion distance is estimated. It is used with the cross-wind-integrated concentration to determine the dimensionless Gaussian concentration at any lateral distance from the plume centerline. Finally, the dimensionless concentration can be converted into a dimensional concentration using the mixed-layer scaling variables.
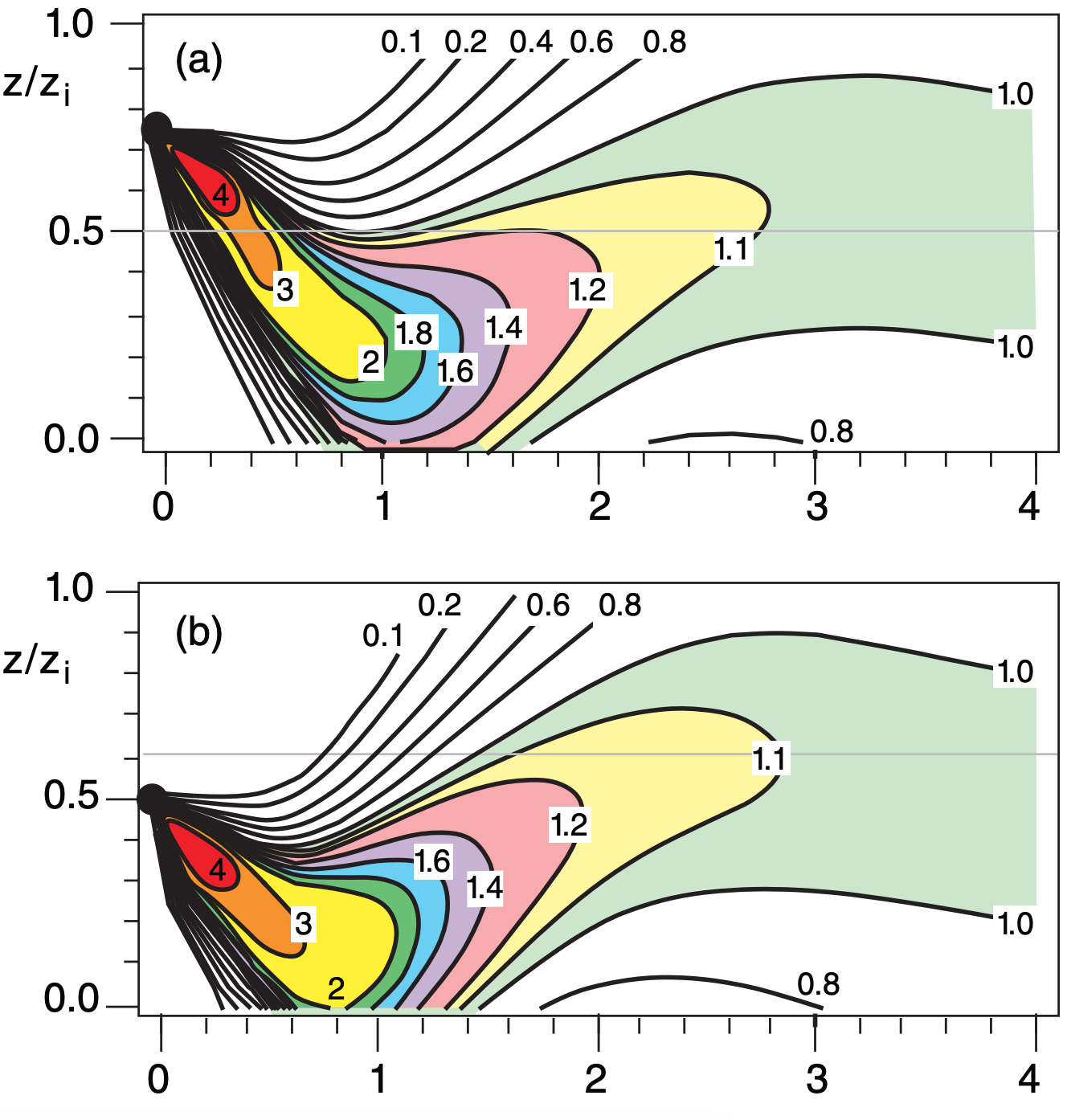
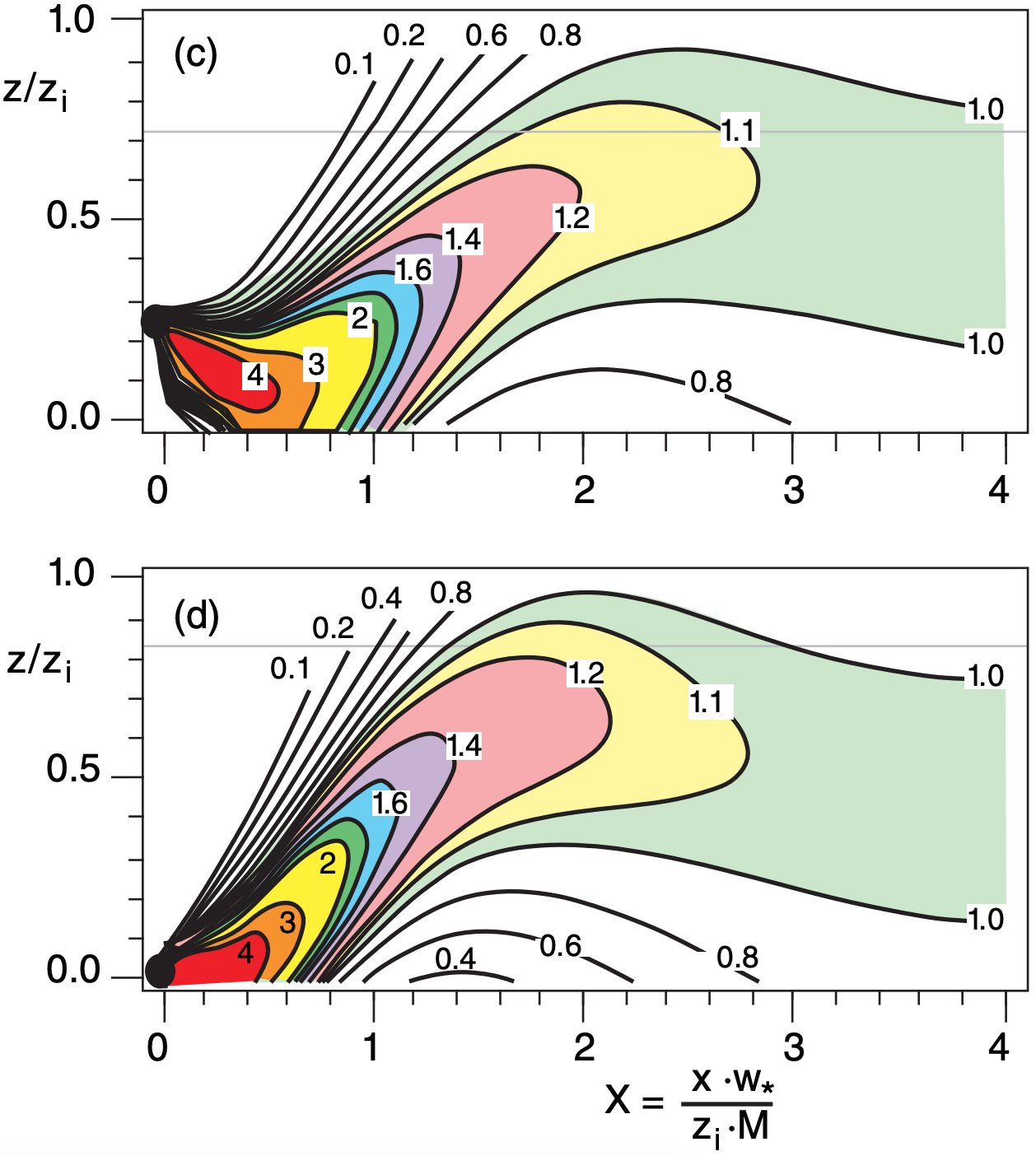
Although this procedure is complex, it is necessary, because non-local dispersion by large convective circulations in the unstable boundary layer works completely differently than the small-eddy dispersion in neutral and stable ABLs. Details of this procedure are given in the next subsection. The whole procedure can be solved on a spreadsheet, which was used to produce Figs. 19.7 and 19.8.
19.7.1. Relevant Variables
19.7.1.1. Physical Variables:
- c = concentration of pollutant (g m–3)
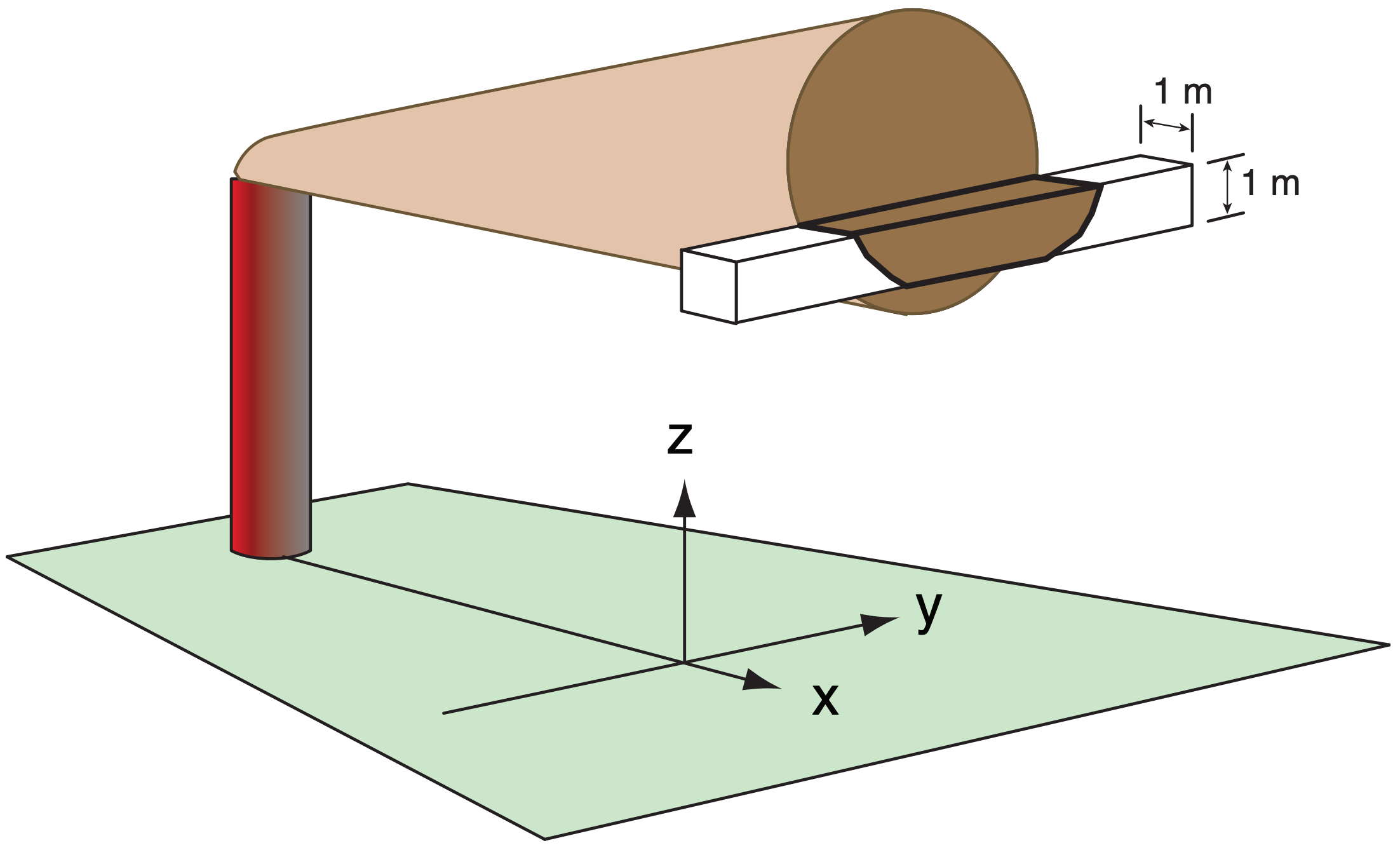
- cy = crosswind-integrated concentration (g m–2), which is the total amount of pollutant within a long, thin box that is 1 m2 on each end, and which extends laterally across the plume at any height z and downwind location x (see Fig. 19.6)
- Q = emission rate of pollutant (g s–1)
- x = distance of a receptor downwind of the stack (m)
- z = height of a receptor above ground (m)
- zCL = height of the plume centerline (center of mass) above the ground (m)
- zs = source height (m) after plume-induced rise
- σy = lateral standard deviation of pollutant (m)
- σz = vertical standard deviation of pollutant (m)
- σzc = vertical standard deviation of crosswind- integrated concentration of pollutant (m)
19.7.1.2. Mixed-Layer Scaling Variables:
FH = effective surface kinematic heat flux (K·m s–1), see Surface Fluxes section of Thermo. chapter
M = mean wind speed (m s–1)
\(\ \begin{align}w_{*}=\left[\frac{|g| \cdot z_{i} \cdot F_{H}}{T_{v}}\right]^{1 / 3}=\bf{\text { Deardorff velocity (m s }^{-1}} \text {) }\tag{19.22}\end{align}\)
≈ 0.08·wB , where wB is the buoyancy velocity
19.7.1.3. Dimensionless Scales:
These are usually denoted by uppercase symbols (except for M and Q, which have dimensions).
\(\ \begin{align}C=\frac{c \cdot z_{i}^{2} \cdot M}{Q}=\text { dimensionless concentration }\tag{19.23}\end{align}\)
\begin{align}C_{y}=\frac{c_{y} \cdot z_{i} \cdot M}{Q}=\text { dimensionless crosswind- integrated concentration }\tag{19.24}\end{align}
\begin{align}X=\frac{x \cdot w_{*}}{z_{i} \cdot M}=
\text { dimensionless downwind distance of receptor from source }\tag{19.25}\end{align}
\begin{align}Y=y / z_{i}=\text{ dimensionless crosswind (lateral) distance of receptor from centerline}\tag{19.26}\end{align}
\begin{align}Z=z / z_{i}=\text{ dimensionless receptor height}\tag{19.27}\end{align}
\begin{align}\mathrm{Z}_{\mathrm{CL}}=z_{\mathrm{CL}} / z_{i}=\text { dimensionless plume centerline
height }\tag{19.28}\end{align}
\begin{align}Z_{s}=z_{s} / z_{i}=\text{ dimensionless source height}\tag{19.29}\end{align}
\begin{align}\sigma_{y d}=\sigma_{y} / z_{i}=\text{dimensionless lateral standard deviation}\tag{19.30}\end{align}
\begin{align}\sigma_{z d c}=\sigma_{z c} / z_{i}=\text{dimensionless vertical standard deviation of crosswind-integrated concentration}\tag{19.31}\end{align}
As stated in more detail earlier, to find the pollutant concentration downwind of a source during convective conditions, three steps are used: (1) Find the plume centerline height. (2) Find the crosswind integrated concentration at the desired x and z location. (3) Find the actual concentration at the desired y location.
19.7.2. Plume Centerline
For neutrally-buoyant emissions, the dimensionless height of the center of mass (= centerline ZCL) varies with dimensionless distance downwind X :
\begin{align}Z_{C L} \approx 0.5+\frac{0.5}{1+0.5 \cdot X^{2}} \cdot \cos \left[2 \pi \frac{X}{\lambda}+\cos ^{-1}\left(2 \cdot Z_{s}-1\right)\right]\tag{19.32}\end{align}
where Zs is the dimensionless source height, and the dimensionless wavelength parameter is λ = 4.
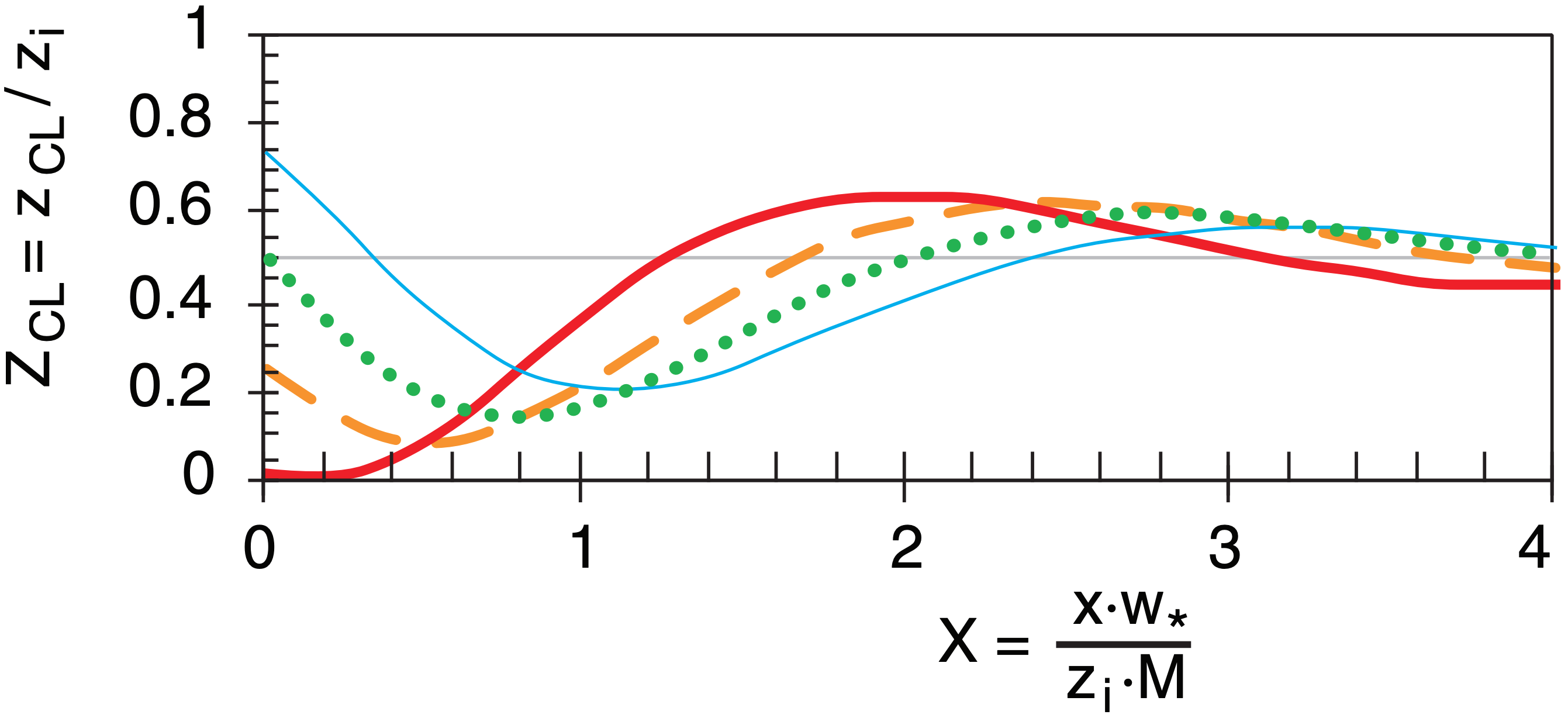
The centerline tends to move down from elevated sources, which can cause high concentrations at ground level (see Fig. 19.7). Then further downwind, they rise a bit higher than half the mixed-layer depth, before reaching a final height at 0.5·zi . For buoyant plumes, the initial downward movement of the centerline is much weaker, or does not occur.
19.7.3. Crosswind-Integrated Concentration
The following algorithm provides a quick approximation for the crosswind-integrated concentration. Find a first guess dimensionless Cy’ as a function of dimensionless height Z using a Gaussian approach for vertical dispersion:
\begin{align}C_{y}^{\prime}=\exp \left[-0.5 \cdot\left(\frac{Z-Z_{C L}}{\sigma_{z d c}^{\prime}}\right)^{2}\right]\tag{19.33}\end{align}
where the prime denotes a first guess, and where the vertical dispersion distance is:
\begin{align}\sigma_{z d c}^{\prime}=a \cdot X\tag{19.34}\end{align}
with a = 0.25 . This calculation is done at K equally-spaced heights between the ground and the top of the mixed layer.
Next, find the average over all heights 0 ≤ Z ≤ 1:
\begin{align}\overline{C_{y}^{\prime}}=\frac{1}{K} \sum_{k=1}^{K} C_{y}^{\prime}\tag{19.35}\end{align}
where index k corresponds to height z . Finally, calculate the revised estimate for dimensionless crosswind-integrated concentration at any height:
\begin{align}C_{y}=C_{y}^{\prime} / \overline{C_{y}^{\prime}}\tag{19.36}\end{align}
Examples are plotted in Fig. 19.8 for various source heights.