19.6: Dispersion in Neutral and Stable Boundary Layers
- Page ID
- 9657
To calculate pollutant concentration at the surface, one needs to know both the height of the plume centerline, and the spread of pollutants about that centerline. Plume rise is the name given to the first issue. Dispersion (from Taylor’s statistical theory) is the second. When they are both used in an expression for the average spatial distribution of pollutants, pollution concentrations can be calculated.
19.6.1. Plume Rise
Ground-level concentration generally decreases as plume-centerline height increases. Hence, plume rise above the physical stack top is often desirable. The centerline of plumes can rise above the stack top due to the initial momentum associated with exit velocity out of the top of the stack, and due to buoyancy if the effluent is hot.
19.6.1.1. Neutral Boundary Layers
Statically neutral situations are found in the residual layer (not touching the ground) during light winds at night. They are also found throughout the bottom of the boundary layer (touching the ground) on windy overcast days or nights.
The height zCL of the plume centerline above the ground in neutral boundary layers is:
\(\ \begin{align}z_{C L}=z_{s}+\left[a \cdot l_{m}^{2} \cdot x+b \cdot l_{b} \cdot x^{2}\right]^{1 / 3}\tag{19.16}\end{align}\)
where a = 8.3 (dimensionless), b = 4.2 (dimensionless), x is distance downwind of the stack, and zs is the physical stack height. This equation shows that the plume centerline keeps rising as distance from the stack increases. It ignores the capping inversion at the ABL top, which would eventually act like a lid on plume rise and upward spread.
A momentum length scale, lm, is defined as:
\(\ \begin{align}l_{m} \approx \frac{W_{o} \cdot R_{o}}{M}\tag{19.17}\end{align}\)
where Ro is the stack-top radius, Wo is stack-top exit velocity of the effluent, and M is the ambient wind speed at stack top. lm can be interpreted as a ratio of vertical emitted momentum to horizontal wind momentum.
A buoyancy length scale, lb, is defined as:
\(\ \begin{align}l_{b} \approx \frac{W_{o} \cdot R_{o}^{2} \cdot|g|}{M^{3}} \cdot \frac{\Delta \theta}{\theta_{a}}\tag{19.18}\end{align}\)
where |g| = 9.8 m s–2 is gravitational acceleration magnitude, ∆θ = θp – θa is the temperature excess of the effluent, θp is the initial stack gas potential temperature at stack top, and θa is the ambient potential temperature at stack top. lb can be interpreted as a ratio of vertical buoyancy power to horizontal power of the ambient wind.
Sample Application (§)
At stack top, effluent velocity is 20 m s–1, temperature is 200°C, emission rate is 250 g s–1 of SO2. The stack is 75 m high with 2 m radius at the top. At stack top, the ambient wind is 5 m s–1, and ambient potential temperature is 20°C. For a neutral boundary layer, plot plume centerline height vs. downwind distance.
Find the Answer
Given: Wo = 20 m s–1, Q = 250 g s–1, zs = 75 m, M = 5 m s–1 , θa = 293 K , θp = 473 K + (9.8 K km–1)·(0.075 km) = 474 K
Find: zCL(x) = ? m.
Use eq. (19.17): lm = (20m s–1)·(2m) / (5m s–1) = 8 m
Use eq. (19.18):
\(\ l_{b} \approx \frac{(20 \mathrm{m} / \mathrm{s}) \cdot(2 \mathrm{m})^{2} \cdot\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)}{(5 \mathrm{m} / \mathrm{s})^{3}} \cdot \frac{(474-293 \mathrm{K})}{293 \mathrm{K}}=3.87 \mathrm{m}\)
Use eq. (19.16):
\(\ z_{C L}=(75 \mathrm{m})+\left[8.3 \cdot(8 \mathrm{m})^{2} \cdot x+4.2 \cdot(3.87 \mathrm{m}) \cdot x^{2}\right]^{1 / 3}\)
This is shown as the solid line on the plot below:
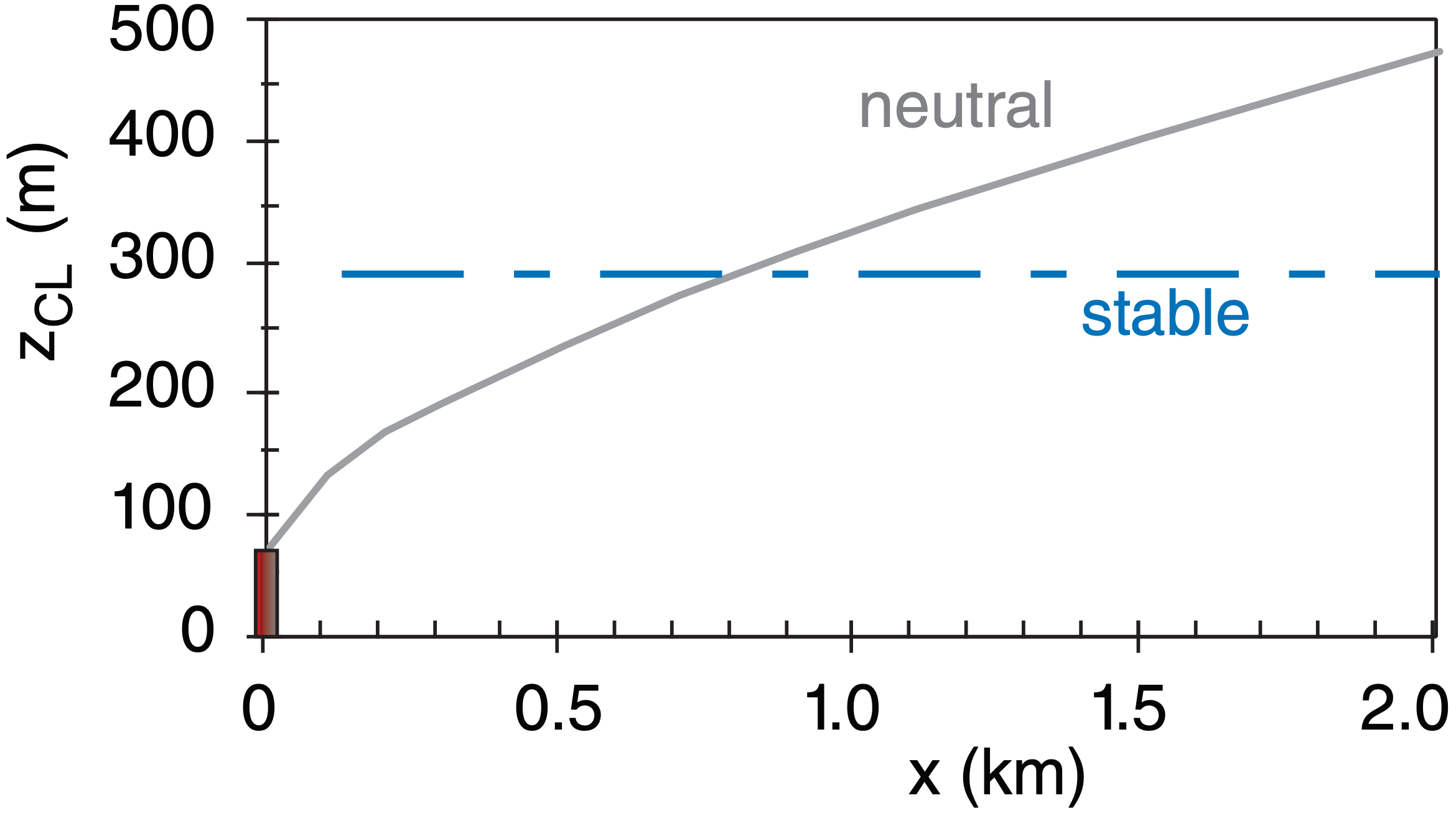
Check: Units OK. Physics OK. Sketch OK.
Exposition: In neutral conditions, the plume continues to rise with downwind distance. However, real plumes usually hit an elevated inversion & stop rising. Use a thermo diagram to locate the inversions aloft.
19.6.1.2. Stable Boundary Layers
In statically stable situations, the ambient potential temperature increases with height. This limits the plume-rise centerline to a final equilibrium height zCLeq above the ground:
\(\ \begin{align} z_{C L e q}=z_{s}+2.6 \cdot\left(\frac{l_{b} \cdot M^{2}}{N_{B V}^{2}}\right)^{1 / 3}\tag{19.19}\end{align}\)
where the Brunt-Väisälä frequency NBV is used as a measure of static stability (see the Atmospheric Stability chapter).
Sample Application
Same as previous example, but for a stable boundary layer with ∆θa/∆z = 5°C km–1. Find zCLeq .
Find the Answer
Given: Wo = 20 m s–1, Q = 250 g s–1, zs = 75 m, M = 5 m s–1 , θp = 474 K, θa = 293 K, ∆θa/∆z = 5°C km–1
Find: ∆zCLeq = ? m , then plot zCLeq vs. x
Use eq. (5.4b) to find the Brunt-Väisälä frequency2: NBV2 = [(9.8m·s–2)/293K]·[5K/1000m] =1.67x10–4 s–2
Use eq. (19.19):
\(\ z_{C L e q}=(75 \mathrm{m})+2.6 \cdot\left(\frac{(3.87 \mathrm{m}) \cdot(5 \mathrm{m} / \mathrm{s})^{2}}{1.67 \times 10^{-4} \mathrm{s}^{-2}}\right)^{1 / 3}\)
zCLeq = zs + ∆zCL eq = 75 m + 216.7 m = 291.75 m.
See dashed line in the previous Sample Application.
Check: Units OK. Physics OK. Sketch OK.
Exposition: The actual plume centerline does not reach the equilibrium height instantly. Instead, it approaches it a bit slower than the neutral plume rise curve plotted in the previous solved ex.
19.6.2. Gaussian Concentration Distribution
For neutral and stable boundary layers (PG types C through F), the sizes of turbulent eddies are relatively small compared to the depth of the boundary layer. This simplifies the problem by allowing turbulent dispersion to be modeled analogously to molecular diffusion. For this situation, the average concentration distribution about the plume centerline is well approximated by a 2-D Gaussian bell curve:
\(\ \begin{align}\begin{aligned}
&c=\frac{Q}{2 \pi \sigma_{y} \sigma_{z} M} \cdot \exp \left[-0.5 \cdot\left(\frac{y}{\sigma_{y}}\right)^{2}\right]\cdot
\left\{\exp \left[-0.5 \cdot\left(\frac{z-z_{C L}}{\sigma_{z}}\right)^{2}\right]+\exp \left[-0.5 \cdot\left(\frac{z+z_{C L}}{\sigma_{z}}\right)^{2}\right]\right\}
\end{aligned}\tag{19.20}\end{align}\)
where Q is the source emission rate of pollutant (g s–1), σy and σz are the plume-spread standard deviations in the crosswind and vertical directions, y is lateral (crosswind) distance of the receptor from the plume centerline, z is vertical distance of the receptor above ground, zCL is the height of the plume centerline above ground, and M is average ambient wind speed at the plume centerline height.
For receptors at the ground (z = 0), eq. (19.20) reduces to:
\(\ \begin{align}c=\frac{Q}{\pi \sigma_{y} \sigma_{z} M} \cdot \exp \left[-0.5 \cdot\left(\frac{y}{\sigma_{y}}\right)^{2}\right] \cdot \exp \left[-0.5 \cdot\left(\frac{z_{C L}}{\sigma_{z}}\right)^{2}\right]\tag{19.21}\end{align}\)
The pattern of concentration at the ground is called a footprint.
The above two equations assume that the ground is flat, and that pollutants that hit the ground are “reflected” back into the air. Also, they do not work for dispersion in statically unstable mixed layers.
To use these equations, the turbulent velocity variances σv2 and σw2 are first found from the equations in the Atmospheric Boundary Layer chapter. Next, plume spread (σy and σz) is found from Taylor’s statistical theory (eqs. 19.13). Plume centerline heights zCL are found from equations in the previous subsection. Finally, they are all used in eqs. (19.20) or (19.21) to find the concentration at a receptor.
Recall that Taylor’s statistical theory states that the plume spread increases with downwind distance. Thus, σy , σz, and zCL are functions of x, which makes concentration c a strong function of x, in spite of the fact that x does not appear explicitly in the two equations above.
Sample Application (§)
Given a “surface” wind speed of 10 m s–1 at 10 m above ground, neutral static stability, boundary layer depth 800 m, surface roughness length 0.1 m, emission rate of 300 g s–1 of passive, non-buoyant SO2, wind speed of 20 m s–1 at plume centerline height, and Lagrangian time scale of 1 minute.
Plot isopleths of concentration at the ground for plume centerline heights of: (a) 100m, (b) 200m
Find the Answer
Given: M = 10 m s–1 at z = 10 m, zo = 0.1 m, M = 20 m s–1 at z = 100 m = zCL, neutral, Q = 300 g s–1 of SO2, tL = 60 s, h = 800 m
Find: c (µg m–3) vs. x (km) and y (km), at z = 0.
Assume zCL is constant.
Use eq. (18.13) from the Atmospheric Boundary Layer (ABL) chapter:
u* = 0.4·(10 m s–1)/ln(10 m/0.1 m) = 0.869 m s–1
(a) Use eqs. (18.25b) & (18.25c) from the ABL chapter:
σv = 1.6·(0.869m s–1)·[1–0.5(100/800)] = 1.3 m s–1
σw = 1.25·(0.869m s–1)·[1–0.5(100/800)] = 1.02 m s–1
Use eq. (19.13a & b) in a spreadsheet to get σy and σz vs.
x. Then use eq. (19.21) to find c at each x and y:
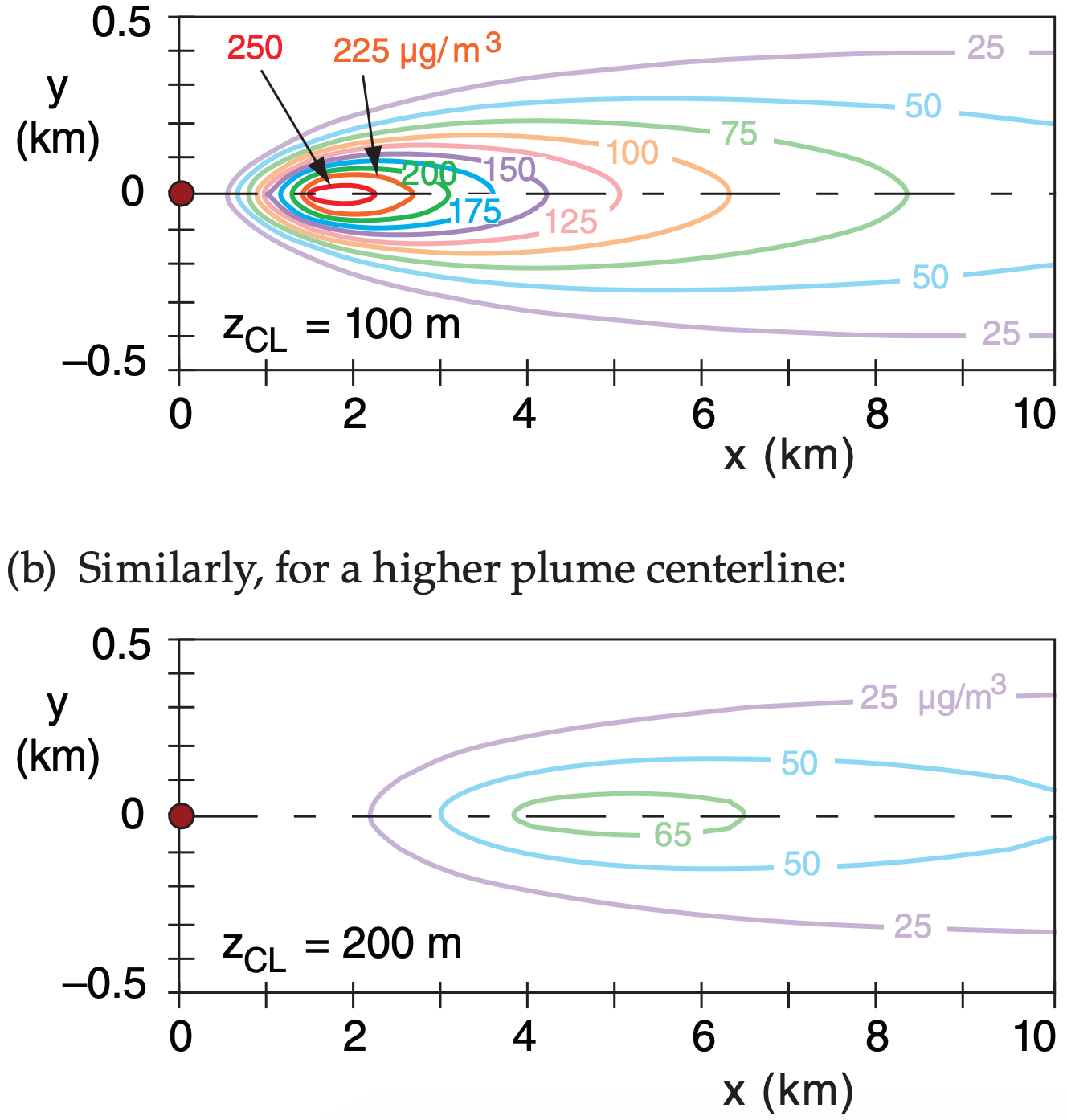
Check: Units OK. Physics OK.
Exposition: These plots show the pollutant footprints. Higher plume centerlines cause lower concentrations at the ground. That is why engineers design tall smoke stacks, and try to enhance buoyant plume rise.
Faster wind speeds also cause more dilution. Because faster winds are often found at higher altitudes, this also favors tall stacks for reducing surface concentrations.


