12.9: Drylines
- Page ID
- 10220
In western Texas, USA, there often exists a boundary between warm humid air to the east, and warm dry air to the west (Fig. 12.36). This boundary is called the dryline. Because the air is hot on both sides of the boundary, it cannot be labeled as a warm or cold front. The map symbol for a dryline is like a warm front, except with open semicircles adjacent to each other, pointing toward the moist air.
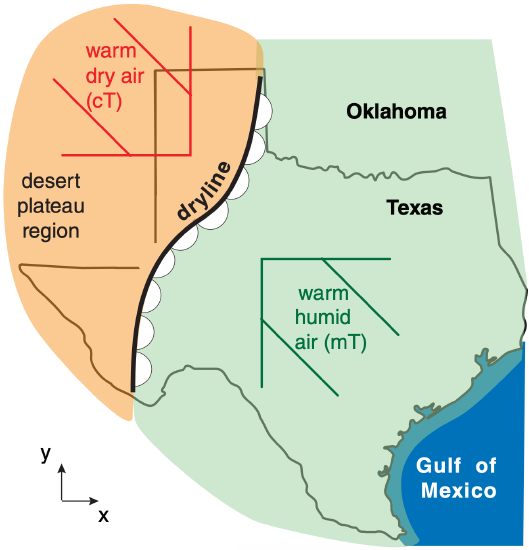
Drylines are observed during roughly 40 to 50% of all days in spring and summer in that part of the world. Similar drylines are observed in other parts of the world.
During midday through afternoon, convective clouds are often triggered along the drylines as the less-dense moist air rides over the denser dry air. Some of these cloud bands grow into organized thunderstorm squall lines that can propagate east from the dryline.
Drylines need not be associated with a wind shift, convergence, vorticity, nor with low pressure. Hence, they do not satisfy the definition of a front. However, sometimes drylines combine with troughs to dynamically contribute to cyclone development.
Drylines in the southwestern USA tend to move eastward during the morning, and return westward during evening. This diurnal cycle is associated with the daily development of a convective mixed layer, interacting with the sloping terrain, via the following mechanism.
Between the Gulf of Mexico (at sea level) and the high-desert plateau of west Texas and New Mexico (roughly 1.5 km above sea level) is a broad region of sloping terrain. Over the high plateaus to the west, deep hot turbulent mixed layers can form in the late afternoon. By night and early morning, after turbulence decays, this thick dry layer of hot air over the plateau becomes a non-turbulent residual layer with nearly adiabatic lapse rate (Fig. 12.37a). Westerly winds advect this dry air eastward, where it overrides cooler, humid air at lower altitudes. Between that elevated residual layer and the moister air below is a strong stable layer such as a temperature inversion.
After sunrise, the warm ground causes a convective mixed-layer to form and grow. The mixed-layer depth is shown by the dashed line in Fig. 12.37b. Because the ground is higher in the west, the top of the mixed layer is able to reach the dry residual-layer air in the west earlier than in the east. When this dry air is entrained downward into the air below, it causes the surface humidity to drop.
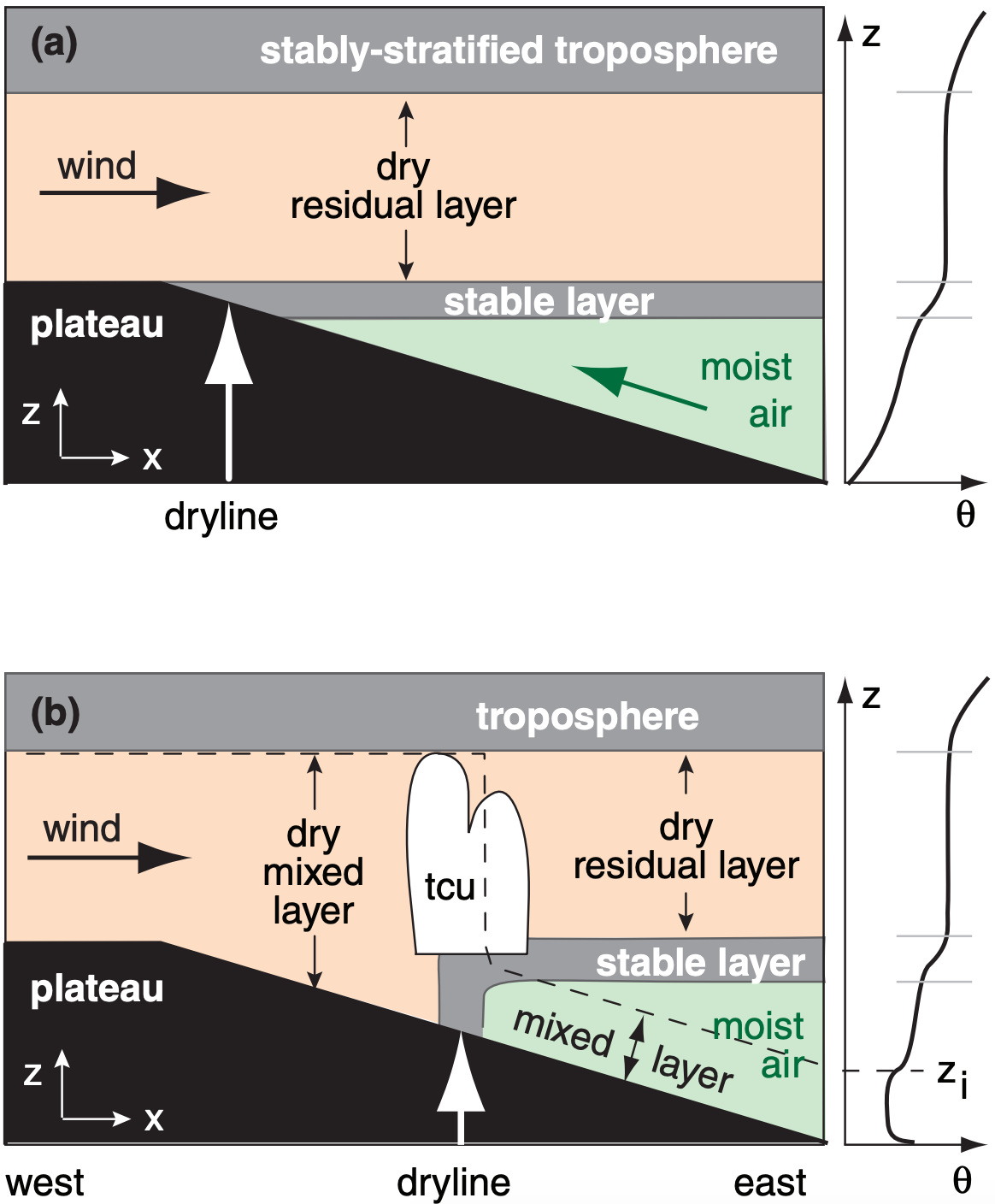
Meanwhile, further east, the top of the mixed layer has yet to reach the dry air aloft, so the humidity is still high there. The dryline separates this moist surface air in the east from the dry air to the west.
As the day continues, the mixed layer in the moist air deepens, allowing the region of dry-air entrainment to spread eastward. This causes the dryline to move eastward as the day progresses. At night, convective turbulence ceases, a stable boundary layer develops, and prevailing low-altitude easterlies advect moist air back toward the west (Fig. 12.37a).
If we assume that initially the inversion is level with respect to sea level, then using geometry, we can see that the progression speed of the dryline eastward ∆x/∆t is directly related to the rate of growth of the mixed layer ∆zi /∆t :
\(\ \begin{align} \frac{\Delta x}{\Delta t}=\frac{\Delta z_{i} / \Delta t}{s}\tag{12.13}\end{align}\)
where s = ∆z/∆x is the terrain slope.
Suppose the early morning stable boundary layer has a linear profile of potential temperature γ = ∆θ/∆z, then the mixed-layer growth proceeds with the square-root of accumulated daytime heating QAk (see the Atmospheric Boundary Layer chapter):
\(\ \begin{align} z_{i}=\left(\frac{2 \cdot Q_{A k}}{\gamma}\right)^{1 / 2}\tag{12.14}\end{align}\)
As a result, the distance ∆x that a dryline moves eastward as a function of time is:
\(\ \begin{align} \Delta x=\frac{1}{s} \cdot\left(\frac{2 \cdot Q_{A k}}{\gamma}\right)^{1 / 2}\tag{12.15}\end{align}\)
Time is hidden in the cumulative heat term QAk.
Sample Application (§)
Suppose the surface heat flux during the day is constant with time at 0.2 K·m s–1 in the desert southwest USA. The early morning sounding has a potential temperature gradient of γ = 10 K km–1. The terrain slope is 1:400. Plot the dryline position with time.
Find the Answer
Given: γ = 10 K km–1, s = 1/400, FH = 0.2 K·m s–1,
Find: ∆x(t) = ? km.
For constant surface flux, cumulative heating is:
\(Q_{A k}=F_{H} \cdot \Delta t\)
where ∆t is time since sunrise.
Thus, eq. (12.15) can be rewritten as:
\(\Delta x=\frac{1}{s} \cdot\left(\frac{2 \cdot F_{H} \cdot \Delta t}{\gamma}\right)^{1 / 2}\)
\(=\frac{400}{1} \cdot\left[\frac{2 \cdot(0.2 \mathrm{K} \cdot \mathrm{m} / \mathrm{s}) \cdot \Delta t}{(0.01 \mathrm{K} / \mathrm{m})}\right]^{1 / 2}\)
Plotting this with a spreadsheet program:
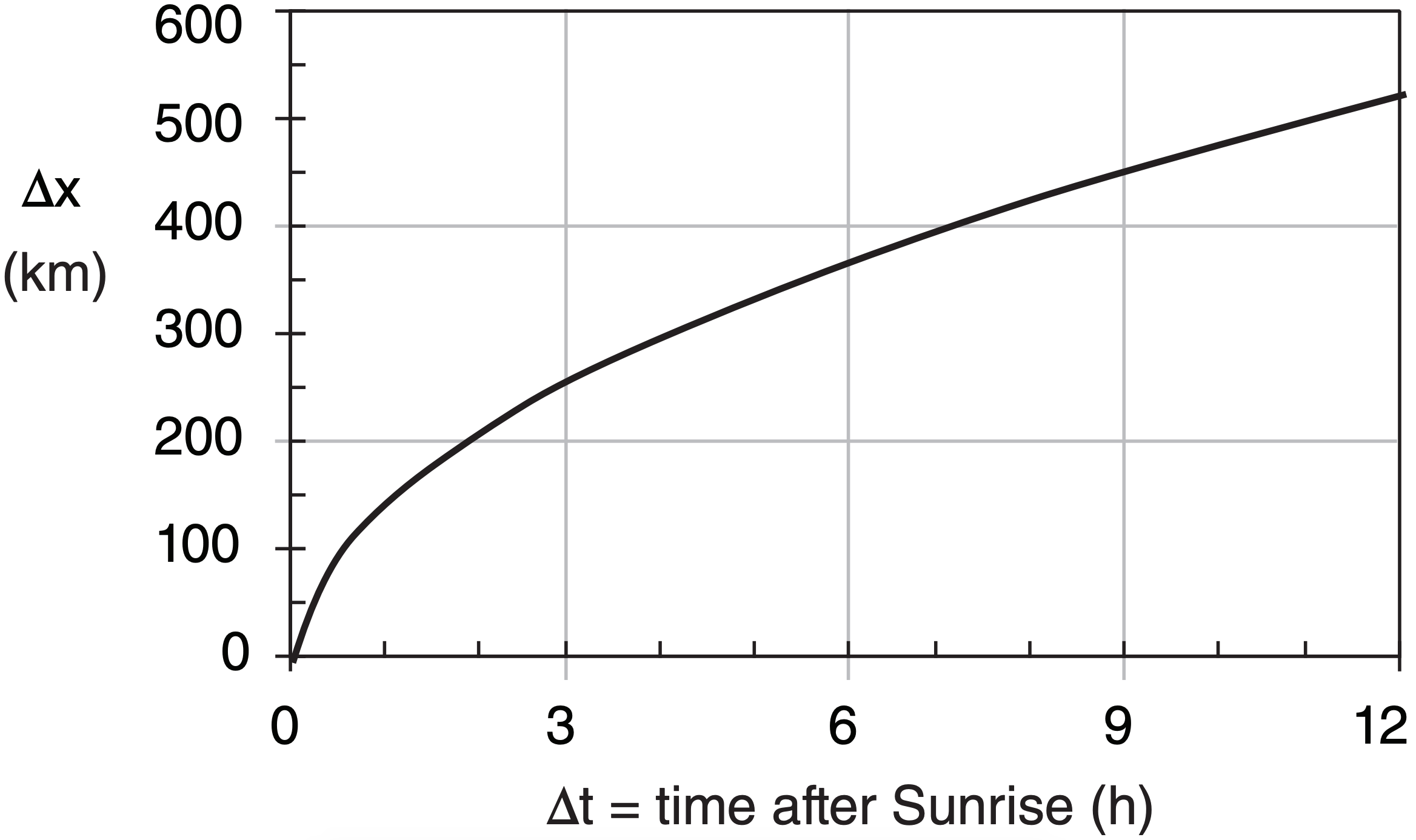
Check: Units OK. Physics OK. Graph reasonable
Exposition: The dryline moves to the east with the square-root of time. Thus, the further east it gets, the slower it goes.


