2.1: 2.2. Flux
- Page ID
- 9534
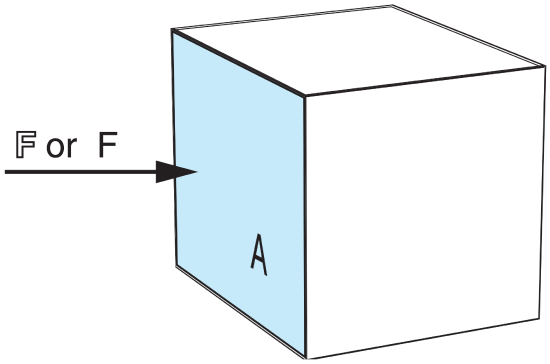
A flux density, F, called a flux in this book, is the transfer of a quantity per unit area per unit time. The area is taken perpendicular (normal) to the direction of flux movement. Examples with metric (SI) units are mass flux (kg· m–2·s–1) and heat flux, ( J·m-2·s–1). Using the definition of a watt (1 W = 1 J·s–1), the heat flux can also be given in units of (W·m–2). A flux is a measure of the amount of inflow or outflow such as through the side of a fixed volume, and thus is frequently used in Eulerian frameworks (Figure 2.7).
Because flow is associated with a direction, so is flux associated with a direction. You must account for fluxes Fx, Fy, and Fz in the x, y, and z directions, respectively. A flux in the positive x-direction (eastward) is written with a positive value of Fx, while a flux towards the opposite direction (westward) is negative.
The total amount of heat or mass flowing through a plane of area A during time interval ∆t is given by:
\(\ \begin{align}Amount=\mathbb{F} \cdot A \cdot \Delta t \tag{2.9}\end{align}\)
For heat, Amount ≡ ∆QH by definition.
Fluxes are sometimes written in kinematic form, F, by dividing by the air density, ρair :
\(\ \begin{align}F=\frac{\mathbb{F}}{\rho_{\text {air}}}\tag{2.10}\end{align}\)
Kinematic mass flux equals the wind speed, M. Kinematic fluxes can also be in the 3 Cartesian directions: Fx, Fy, and Fz.
[CAUTION: Do not confuse the usage of the symbol M. Here it means “wind speed”. Earlier it meant “mean anomaly”. Throughout this book, many symbols will be re-used to represent different things, due to the limited number of symbols. Even if a symbol is not defined, you can usually determine its meaning from context.]
Heat fluxes FH can be put into kinematic form by dividing by both air density ρair and the specific heat for air Cp, which yields a quantity having the same units as temperature times wind speed (K·m·s–1)
\(\ \begin{align}F_{H}=\frac{\mathbb{F}_{H}}{\rho_{a i r} \cdot C_{p}} \quad for\ heat\ only \tag{2.11}\end{align}\)
For dry air (subscript “d”) at sea level:
ρair · Cpd = 1231 (W·m–2) / (K·m·s–1) = 12.31 mb·K–1 = 1.231 kPa·K–1 .
The reason for sometimes expressing fluxes in kinematic form is that the result is given in terms of easily measured quantities. For example, while most people do not have “Watt” meters to measure the normal “dynamic” heat flux, they do have thermometers and anemometers. The resulting temperature times wind speed has units of a kinematic heat flux (K·m·s–1). Similarly, for mass flux it is easier to measure wind speed than kilograms of air per area per time.
Heat fluxes can be caused by a variety of processes. Radiative fluxes are radiant energy (electromagnetic waves or photons) per unit area per unit time. This flux can travel through a vacuum. Advective flux is caused by wind blowing through an area, and carrying with it warmer or colder temperatures. For example a warm wind blowing toward the east causes a positive heat-flux component FHx in the x-direction. A cold wind blowing toward the west also gives positive FHx. Turbulent fluxes are caused by eddy motions in the air, while conductive fluxes are caused by molecules bouncing into each other.
Sample Application
The mass flux of air is 1 kg·m–2·s–1 through a door opening that is 1 m wide by 2.5 m tall. What amount of mass of air passes through the door each minute, and what is the value of kinematic mass flux?
Find the Answer
Given: area A = (1 m) · (2.5 m) = 2.5 m2
F = 1 kg·m–2·s–1
Find: (a) Amount = ? kg, and (b) F = ? m·s–1
Sketch: (see Figure 2.7)
a) Use eq. (2.9):
Amount = (1 kg·m–2·s–1)·(2.5 m2)· (1 min)·(60 s min–1) = 150 kg.
(b) Assume: ρ = 1.225 kg·m–3 at sea-level
Use eq. (2.10):
F = (1 kg·m–2·s–1) / (1.225 kg·m–3) = 0.82 m·s–1.
Check: Units OK. Sketch OK. Physics OK.
Exposition: The kinematic flux is equivalent to a very light wind speed of less than 1 m s–1 blowing through the doorway, yet it transports quite a large amount of mass each minute.
Sample Application
If the heat flux from the sun that reaches the Earth’s surface is 600 W m–2, find the flux in kinematic units.
Find the Answer
Given: FH = 600 W m–2
Find: FH = ? K·m s–1
Assume: sea level.
Use eq. (2.11)
FH = (600 W m–2) / [1231 (W·m–2) / (K·m·s–1) ] = 0.487 K·m s–1
Check: Units OK. Physics OK.
Exposition: This amount of radiative heat flux is equivalent to an advective flux of a 1 m s–1 wind blowing air with temperature excess of about 0.5°C.


