2.0: Orbital Factors

2.1.1. Planetary Orbits

Johannes Kepler, the 17^th century astronomer, discovered that planets in the solar system have elliptical orbits around the sun. For most planets in the solar system, the eccentricity (deviation from circular) is relatively small, meaning the orbits are nearly circular. For circular orbits, he also found that the time period Y of each orbit is related to the distance R of the planet from the sun by:

\(\ \begin{align}Y=a_{1} \cdot R^{3 / 2}\tag{2.1}\end{align}\)

Parameter a₁ ≈ 0.1996 d·(Gm)^–3/2, where d is Earth days, and Gm is gigameters = 10⁶ km.

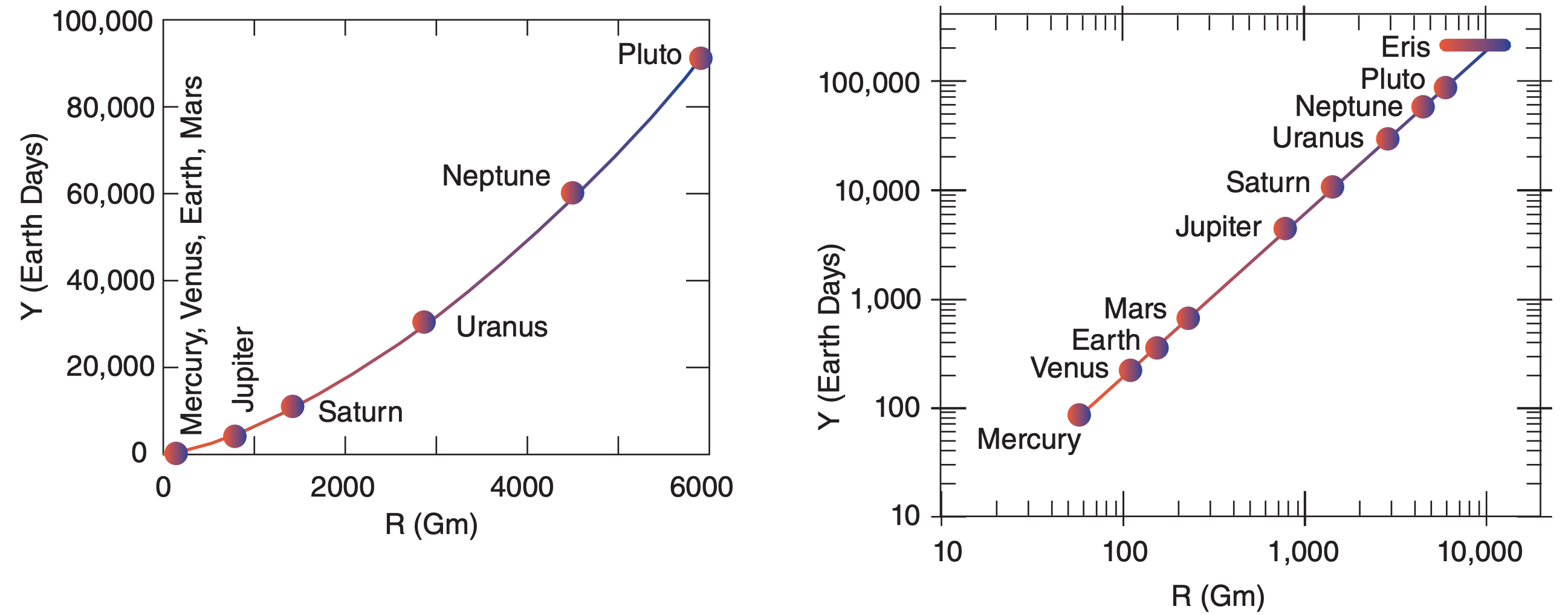
Figs. 2.1a & b show the orbital periods vs. distances for the planets in our solar system. These figures show the duration of a year for each planet, which affect the seasons experienced on the planet.

2.1.2. Orbit of the Earth

The Earth and the moon rotate with a sidereal (relative to the stars) period of 27.32 days around their common center of gravity, called the Earthmoon barycenter. (Relative to the moving Earth, the time between new moons is 29.5 days.) Because the mass of the moon (7.35x10²² kg) is only 1.23% of the mass of the Earth (Earth mass is 5.9726x10²⁴ kg), the barycenter is much closer to the center of the Earth than to the center of the moon. This barycenter is 4671 km from the center of the Earth, which is below the Earth’s surface (Earth radius is 6371 km).

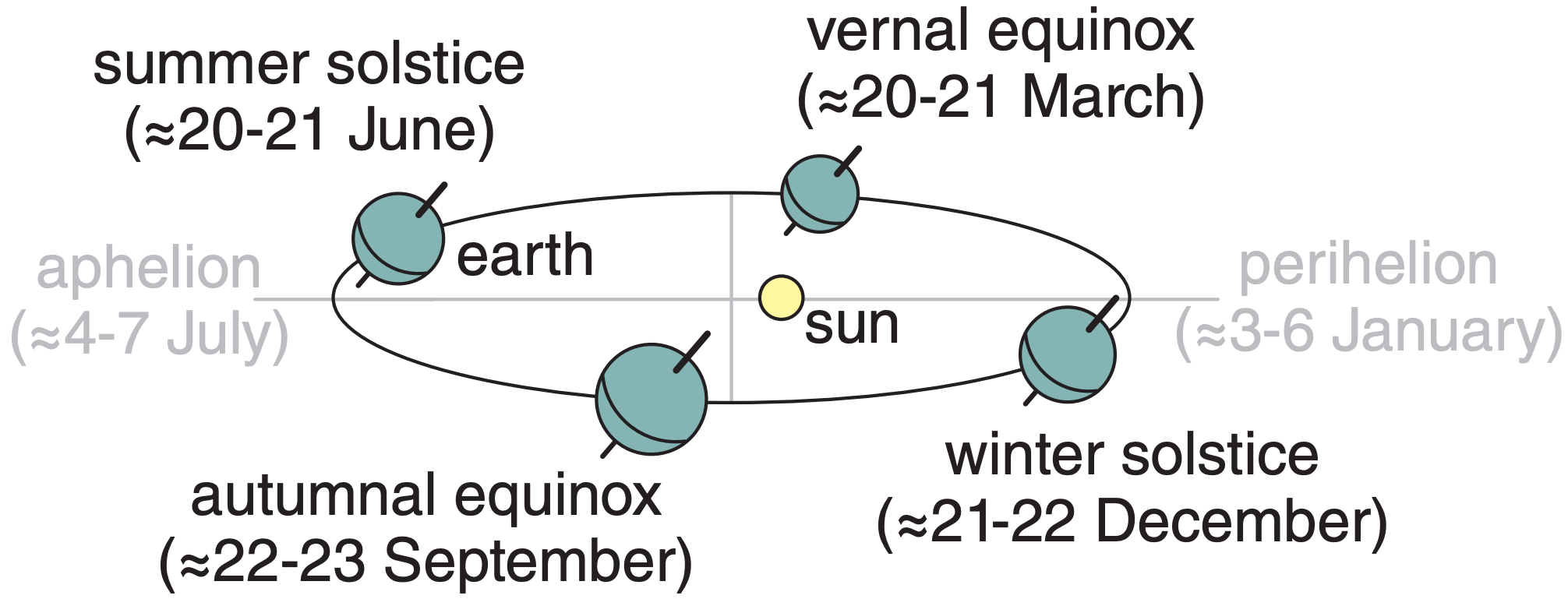
To a first approximation, the Earth-moon barycenter orbits around the sun in an elliptical orbit (Figure 2.2, thin-line ellipse) with sidereal period of P = 365.256363 days. Length of the semi-major axis (half of the longest axis) of the ellipse is a = 149.598 Gm. This is almost equal to an astronomical unit (au), where 1 au = 149,597,870.691 km.

Semi-minor axis (half the shortest axis) length is b = 149.090 Gm. The center of the sun is at one of the foci of the ellipse, and half the distance between the two foci is c = 2.5 Gm, where a² = b² + c². The orbit is close to circular, with an eccentricity of only about e ≈ c/a = 0.0167 (a circle has zero eccentricity).

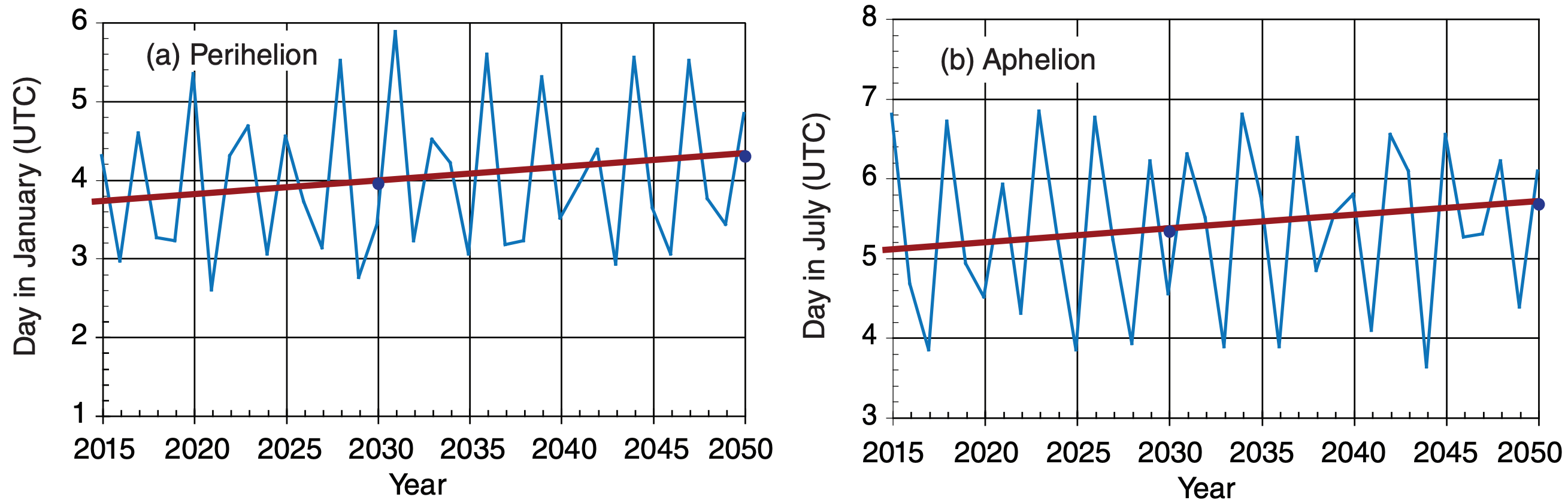
The closest distance (perihelion) along the major axis between the Earth and sun is a – c = 146.96 Gm and occurs at about d_p ≈ 4 January. The farthest distance (aphelion) is a + c = 151.96 Gm and occurs at about 5 July. The dates for the perihelion and aphelion jump a day or two from year to year because the orbital period is not exactly 365 days. Figs. 2.3 show these dates at the prime meridian (Greenwich), but the dates will be slightly different in your own time zone. Also, the dates of the perihelion and aphelion gradually become later by 1 day every 58 years, due to precession (shifting of the location of the major and minor axes) of the Earth’s orbit around the sun (see the Climate chapter).

Figure 2.1 a (linear) & b (log-log) Planetary orbital periods versus distance from sun. Eris (136199) and Pluto (134340) are dwarf planets. Eris, larger than Pluto, has a very elliptical orbit. (a) Linear graph. (b) Log-log graph. (See Appendix A for comparison of various graph formats.)

Sample Application

Verify that eq. (2.1) gives the correct orbital period of one Earth year.

Find the Answer

Given: R = 149.6 Gm avg. distance sun to Earth.

Find: Y = ? days, the orbital period for Earth

Use eq. (2.1):

Y = (0.1996 d·(Gm)^–3/2) · [(149.6 Gm)^1.5] = 365.2 days.

Check: Units OK. Sketch OK. Almost 1 yr.

Exposition: In 365.0 days, the Earth does not quite finish a complete orbit. After four years this shortfall accumulates to nearly a day, which we correct using a leap year with an extra day (see Chapter 1).

Figure 2.2 Geometry of the Earth’s orbit, as viewed from above Earth’s North Pole. (Not to scale.) Dark wavy line traces the Earthcenter path, while the thin smooth ellipse traces the barycenter path.

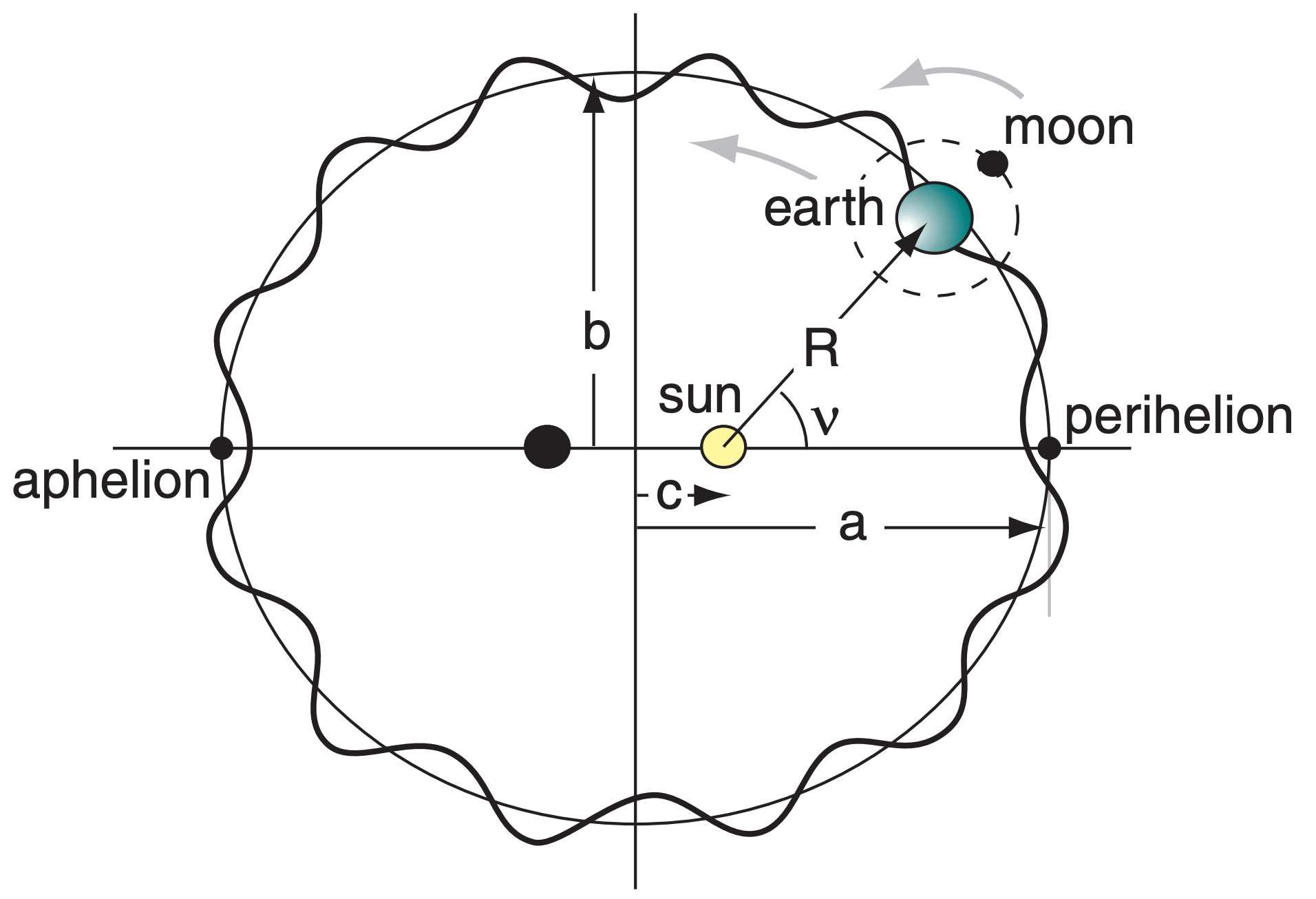
Because the Earth is rotating around the Earthmoon barycenter while this barycenter is revolving around the sun, the location of the center of the Earth traces a slightly wiggly path as it orbits the sun. This path is exaggerated in Figure 2.2 (thick line).

Define a relative Julian Day, d, as the day of the year. For example, 15 January corresponds to d = 15. For 5 February, d = 36 (which includes 31 days in January plus 5 days in February).

The angle at the sun between the perihelion and the location of the Earth (actually to the Earth-moon barycenter) is called the true anomaly ν (see Figure 2.2). This angle increases during the year as the day d increases from the perihelion day (about dp = 4; namely, about 4 January). According to Kepler’s second law, the angle increases more slowly when the Earth is further from the sun, such that a line connecting the Earth and the sun will sweep out equal areas in equal time intervals.

An angle called the mean anomaly M is a simple, but good approximation to ν. It is defined by:

\(\ \begin{align}M=C \cdot \dfrac{d-d_{p}}{P}\tag{2.2}\end{align}\)

where P = 365.256363 days is the (sidereal) orbital period and C is the angle of a full circle (C = 2·π radians = 360°. Use whichever is appropriate for your calculator, spreadsheet, or computer program.)

Because the Earth’s orbit is nearly circular, ν ≈ M. A better approximation to the true anomaly for the elliptical Earth orbit is

\(\ \begin{align}v \approx M+\left[2 e-\left(e^{3} / 4\right)\right] \cdot \sin (M)+\left[(5 / 4) \cdot e^{2}\right] \cdot \sin (2 M) + [(13/12)\cdot e^3]\cdot sin(3M)\tag{2.3a}\end{align}\)

or

\(\ \begin{align}\mathbf{v} \approx M+0.033398 . \sin (M)+0.0003486 \cdot \sin (2 \cdot M)+0.0000050 \cdot sin(3 \cdot M)\tag{2.3b}\end{align}\)

for both ν and M in radians, and e = 0.0167.

The distance R between the sun and Earth (actually to the Earth-moon barycenter) as a function of time is

\(\ \begin{align} R=a \cdot \dfrac{1-e^{2}}{1+e \cdot \cos (v)}\tag{2.4}\end{align}\)

where e = 0.0167 is eccentricity, and a = 149.457 Gm is the semi-major axis length. If the simple approximation of ν ≈ M is used, then angle errors are less than 2° and distance errors are less than 0.06%.

Figure 2.3 Dates (UTC) of the (a) perihelion and (b) aphelion, & their trends (thick line). From the US Naval Observatory.

http:// aa.usno.navy.mil/data/docs/EarthSeasons.php

Sample Application(§)

Use a spreadsheet to find the true anomaly and sun-Earth distance for several days during the year.

Find the Answer

Given: d_p = 4 Jan. P = 365.25 days.

Find: ν = ?° and R = ? Gm

Sketch: (same as Fig 2.2)

For example, for 15 Feb, d = 46

Use eq. (2.2):

M = (2 · 3.14159)·(46–4)/ 365.256363 = 0.722 radians

Use eq. (2.3b):

ν =0.722 +0.0333988·sin(0.722) + 0.0003486·sin(1.444) + 0.000005·sin(2.166) = 0.745 radians

Use eq. (2.4):

R = (149.457Gm)·(1 – 0.01672)/[1+0.0167·cos(0.745)] = (149.457Gm) · 0.99972 / 1.012527 = 147.60 Gm

Repeating this calculation on a spreadsheet for several days, and comparing M vs. ν and R(M) vs. R(ν) , gives:

Date	d	M (rad)	ν (rad)	R(M) (Gm)	R(ν) (Gm)
4 Jan	4	0	0	146.96	146.96
18 Jan	18	0.241	0.249	147.03	147.04
1 Feb	32	0.482	0.497	147.24	147.25
15 Feb	46	0.722	0.745	147.57	147.60
1 Mar	60	0.963	0.991	1 148.00	148.06
15 Mar	74	1.204	1.236	148.53	148.60
29 Mar	88	1.445	1.487	149.10	149.18
12 Apr	102	1.686	1.719	149.70	149.78
26 Apr	116	1.927	1.958	150.29	150.36
21 Jun	172	2.890	2.898	151.87	151.88
23 Sep	266	4.507	4.474	149.93	150.01
22 Dec	356	6.055	6.047	147.02	147.03

Check: Units OK. Physics OK.

Exposition: Because M and ν are nearly equal, you can use M instead of ν in eq. (2.4), with good accuracy

Figure 2.4 Relationship of declination angle δ_s to tilt of the Earth’s axis, for a day near northern-hemisphere summer.

Table 2-1 . Dates and times (UTC) for northern hemisphere equinoxes and solstices. Format: dd hhmm gives day (dd), hour (hh) and minutes (mm). From the US Naval Observatory. http://aa.usno.navy.mil/data/docs/ EarthSeasons.php
Year	Spring Equinox (March)	Summer Solstice (June)	Fall Equinox (Sept.)	Winter Solstice (Dec.)
2015	5 20 2245	21 1638	23 0820	22 0448
2016	20 0430	20 2234	22 1421	21 1044
2017	20 1028	21 0424	22 2002	21 1628
2018	20 1615	21 1007	23 0154	21 2222
2019	20 2158	21 1554	23 0750	22 0419
2020	20 0349	20 2143	22 1330	21 1002
2021	20 0937	21 0332	22 1921	1 21 1559
2022	20 1533	21 0914	4 23 0104	4 21 2148
2023	20 2124	21 1458	23 0650	22 0327
2024	20 0306	20 2051	22 1244	21 0921
2025	20 0901	21 0242	22 1819	21 1503

Figure 2.5 Dates (UTC) of northern-hemisphere seasons relative to Earth’s orbit.

The distance R between the sun and Earth (actually to the Earth-moon barycenter) as a function of time is

\(\ \begin{align} R=a \cdot \dfrac{1-e^{2}}{1+e \cdot \cos (v)}\tag{2.4}\end{align}\)

where e = 0.0167 is eccentricity, and a = 149.457 Gm is the semi-major axis length. If the simple approximation of ν ≈ M is used, then angle errors are less than 2° and distance errors are less than 0.06%.

2.1.3. Seasonal Effects

The tilt of the Earth’s axis relative to a line perpendicular to the ecliptic (i.e., the orbital plane of the Earth around the sun) is presently Φ_r = 23.44° = 0.409 radians. The direction of tilt of the Earth’s axis is not fixed relative to the stars, but wobbles or precesses like a top with a period of about 25,781 years. Although this is important over millennia (see the Climate chapter), for shorter time intervals (up to a century) the precession is negligible, and you can assume a fixed tilt.

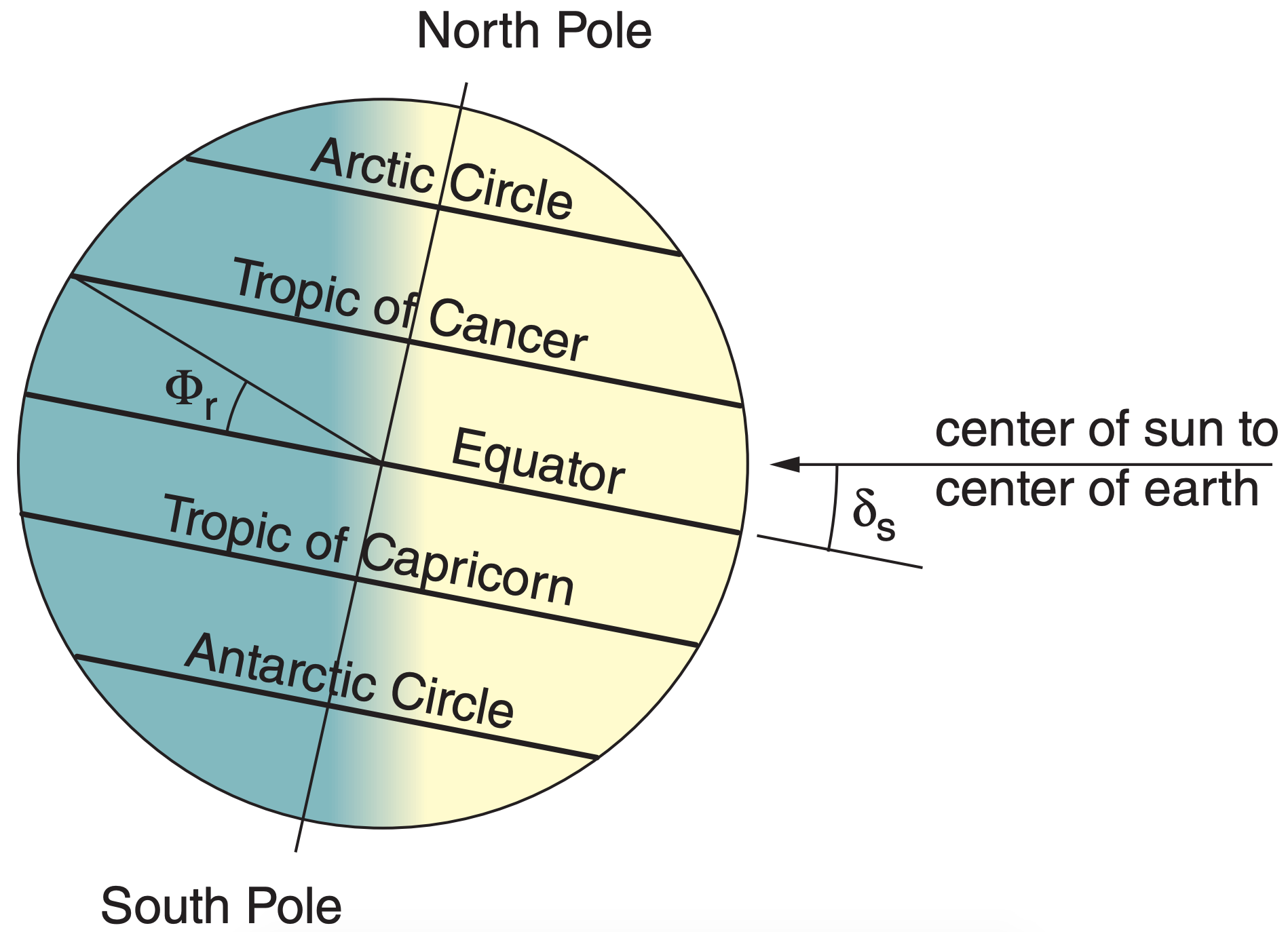
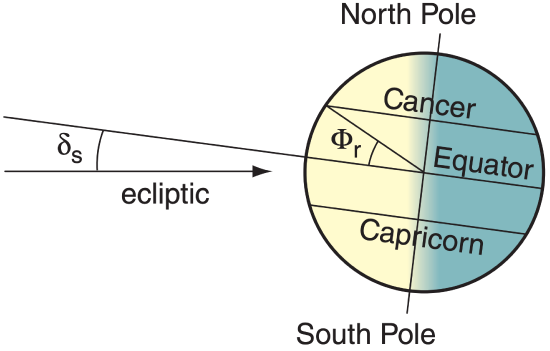
The solar declination angle δ_s is defined as the angle between the ecliptic and the plane of the Earth’s equator (Figure 2.4). Assuming a fixed orientation (tilt) of the Earth’s axis as the Earth orbits the sun, the solar declination angle varies smoothly as the year progresses. The north pole points partially toward the sun in summer, and gradually changes to point partially away during winter (Figure 2.5).

Although the Earth is slightly closer to the sun in winter (near the perihelion) and receives slightly more solar radiation then, the Northern Hemisphere receives substantially less sunlight in winter because of the tilt of the Earth’s axis. Thus, summers are warmer than winters, due to Earth-axis tilt.

The solar declination angle is greatest (+23.44°) on about 20 to 21 June (summer solstice in the Northern Hemisphere, when daytime is longest) and is most negative ( –23.44°) on about 21 to 22 December (winter solstice, when nighttime is longest). The vernal equinox (or spring equinox, near 20 to 21 March) and autumnal equinox (or fall equinox, near 22 to 23 September) are the dates when daylight hours equal nighttime hours (“eqi nox” literally translates to “equal night”), and the solar declination angle is zero.

Astronomers define a tropical year (= 365.242190 days) as the time from vernal equinox to the next vernal equinox. Because the tropical year is not an integral number of days, the Gregorian calendar (the calendar adopted by much of the western world) must be corrected periodically to prevent the seasons (dates of summer solstice, etc.) from shifting into different months.

To make this correction, a leap day (29 Feb) is added every 4^th year (i.e., leap years, are years divisible by 4), except that years divisible by 100 don’t have a leap day. However, years divisible by 400 do have a leap day (for example, year 2000). Because of all these factors, the dates of the solstices, equinoxes, perihelion, and aphelion jump around a few days on the Gregorian calendar (Table 2-1 and Figs. 2.3), but remain in their assigned months.

The solar declination angle for any day of the year is given by

\(\ \begin{align}\delta_{S} \approx \Phi_{r} \cdot \cos \left[\dfrac{C \cdot\left(d-d_{r}\right)}{d_{y}}\right]\tag{2.5}\end{align}\)

where d is Julian day, and d_r is the Julian day of the summer solstice, and d_y = 365 (or = 366 on a leap year) is the number of days per year. For years when the summer solstice is on 21 June, d_r = 172. This equation is only approximate, because it assumes the Earth’s orbit is circular rather than elliptical. As before, C = 2·π radians = 360° (use radians or degrees depending on what your calculator, spreadsheet, or computer program expects).

By definition, Earth-tilt angle (Φ_r = 23.44°) equals the latitude of the Tropic of Cancer in the Northern Hemisphere (Figure 2.4). Latitudes are defined to be positive in the Northern Hemisphere. The Tropic of Capricorn in the Southern Hemisphere is the same angle, but with a negative sign. The Arctic Circle is at latitude 90° – Φ_r = 66.56°, and the Antarctic Circle is at latitude –66.56° (i.e., 66.56°S). During the Northern-Hemisphere summer solstice: the solar declination angle equals Φ_r ; the sun at noon is directly overhead (90° elevation angle) at the Tropic of Cancer; and the sun never sets that day at the Arctic Circle.

Sample Application

Find the solar declination angle on 5 March.

Find the Answer

Assume: Not a leap year

Given: d = 31 Jan + 28 Feb + 5 Mar = 64.

Find: δ_s = ?°

Sketch:

Use eq. (2.5):

δ_s = 23.44° · cos[360°·(64–172)/365] = 23.44° · cos[–106.521°] = –6.67°

Check: Units OK. Sketch OK. Physics OK.

Exposition: On the vernal equinox (21 March), the angle should be zero. Before that date, it is winter and the declination angle should be negative. Namely, the ecliptic is below the plane of the equator. In spring and summer, the angle is positive. Because 5 March is near the end of winter, we expect the answer to be a small negative angle.

2.1.4. Daily Effects

As the Earth rotates about its axis, the local elevation angle Ψ of the sun above the local horizon rises and falls. This angle depends on the latitude ϕ and longitude λ_e of the location:

\(\ \begin{align} \sin (\Psi)=& \sin (\phi) \cdot \sin \left(\delta_{S}\right)- \cos (\phi) \cdot \cos \left(\delta_{S}\right) \cdot \cos \left[\dfrac{C \cdot t_{U T C}}{t_{d}}+\lambda_{e}\right] \tag{2.6} \end{align}\)

Time of day t_UTC is in UTC, C = 2π radians = 360° as before, and the length of the day is t_d. For t_UTC in hours, then td = 24 h. Latitudes are positive north of the equator, and longitudes are positive east of the prime meridian. The sin(Ψ) relationship is used later in this chapter to calculate the daily cycle of solar energy reaching any point on Earth.

[CAUTION: Don’t forget to convert angles to radians if required by your spreadsheet or programming language.]

Sample Application(§)

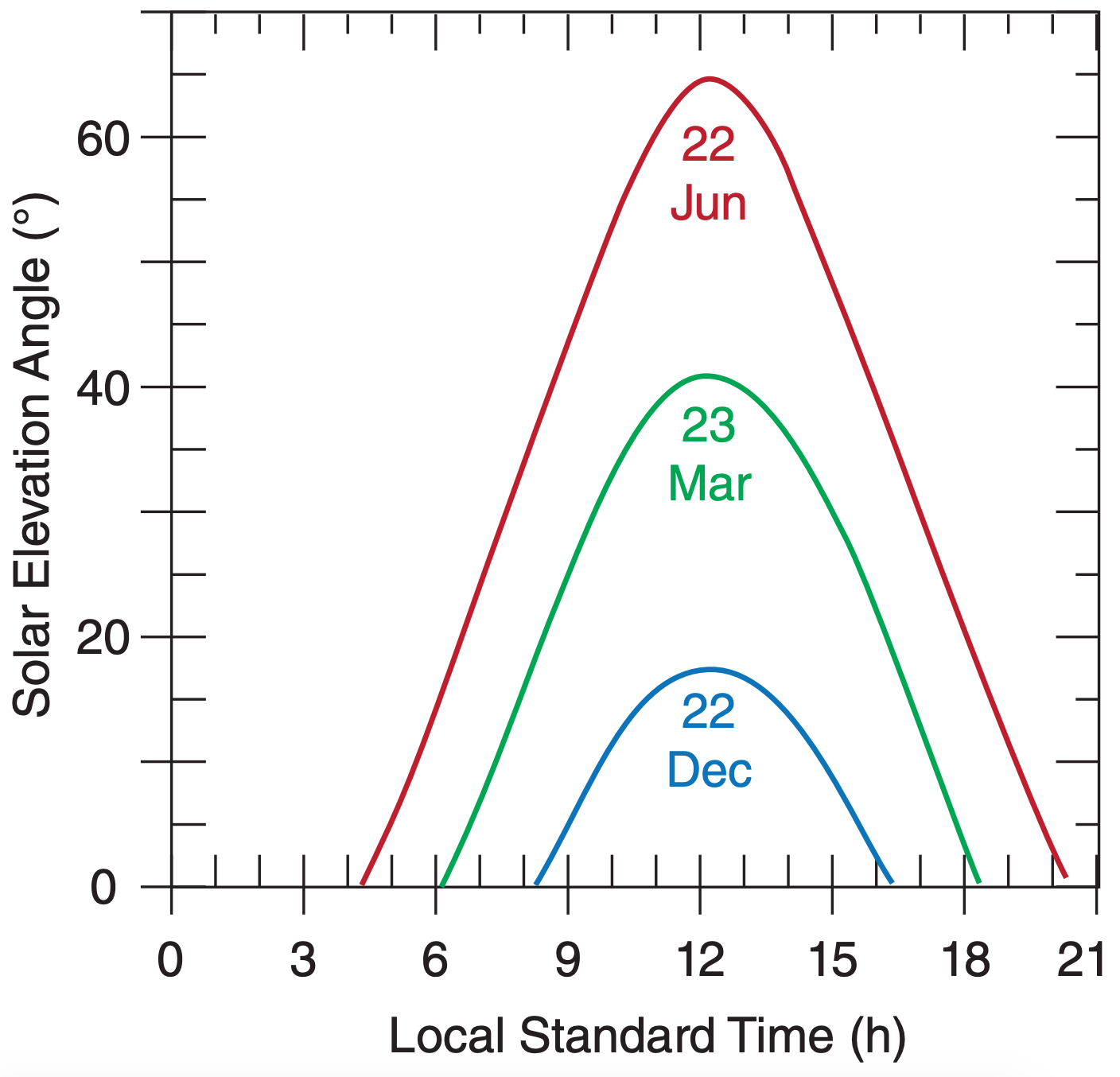
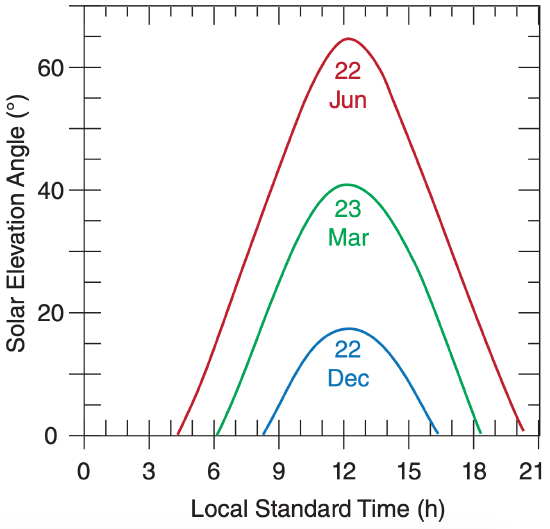
Use a spreadsheet to plot elevation angle vs. time at Vancouver, for 21 Dec, 23 Mar, and 22 Jun. Plot these three curves on the same graph.

Find the Answer

Given: Same as previous Sample Application, except d = 355, 82, 173.

Find: Ψ = ?°. Assume not a leap year.

A portion of the tabulated results are shown below, as well as the full graph.

	Ψ (°)
t (h)	21 Dec	23 Mar	22 Jun
3	0.0	0.0	0.0
4	0.0	0.0	0.0
5	0.0	0.0	6.6
6	0.0	0.0	15.6
7	0.0	7.8	25.1
8	0.0	17.3	34.9
9	5.7	25.9	44.5
10	11.5	33.2	53.4
11	15.5	38.4	60.5
12	17.2	40.8	64.1
13	16.5	39.8	62.6

Check: Units OK. Physics OK. Graph OK.

Exposition: Summers are pleasant with long days. The peak elevation does not happen precisely at local noon, because Vancouver is not centered within its time zone.

The local azimuth angle α of the sun relative to north is

\(\ \begin{align}cos (\alpha)=\dfrac{\sin \left(\delta_{s}\right)-\sin (\phi) \cdot \cos (\zeta)}{\cos (\phi) \cdot \sin (\zeta)}\tag{2.7}\end{align}\)

where ζ = C/4 – Ψ is the zenith angle. After noon, the azimuth angle might need to be corrected to be α = C – α, so that the sun sets in the west instead of the east. Figure 2.6 shows an example of the elevation and azimuth angles for Vancouver (latitude = 49.25°N, longitude = 123.1°W = – 123.1°E) during the solstices and equinoxes.

Figure 2.6 Position (solid lines) of the sun for Vancouver, Canada for various seasons. September 21 and March 23 nearly coincide. Isochrones are dashed. All times are Pacific standard time.

2.1.5. Sunrise, Sunset & Twilight

Geometric sunrise and sunset occur when the center of the sun has zero elevation angle. Apparent sunrise/set are defined as when the top of the sun crosses the horizon, as viewed by an observer on the surface. The sun has a finite radius corresponding to an angle of 0.267° when viewed from Earth. Also, refraction (bending) of light through the atmosphere allows the top of the sun to be seen even when it is really 0.567° below the horizon. Thus, apparent sunrise/set occurs when the center of the sun has an elevation angle of –0.833°.

When the apparent top of the sun is slightly below the horizon, the surface of the Earth is not receiving direct sunlight. However, the surface can still receive indirect light scattered from air molecules higher in the atmosphere that are illuminated by the sun. The interval during which scattered light is present at the surface is called twilight. Because twilight gradually fades as the sun moves lower below the horizon, there is no precise definition of the start of sunrise twilight or the end of sunset twilight.

Arbitrary definitions have been adopted by different organizations to define twilight. Civil twilight occurs while the sun center is no lower than –6°, and is based on the ability of humans to see objects on the ground. Military twilight occurs while the sun is no lower than –12°. Astronomical twilight ends when the skylight becomes sufficiently dark to view certain stars, at solar elevation angle –18°.

Table 2-2 summarizes the solar elevation angle Ψ definitions used for sunrise, sunset and twilight. All of these angles are at or below the horizon.

Table 2-2. Elevation angles for diurnal events.
Event	Ψ (°)	Ψ (radians)
Sunrise & Sunset:
Geometric	0	0
Apparent	–0.833	–0.01454
Twilight:
Civil	–6	–0.10472
Military	–12	–0.20944
Astronomical	–18	–0.31416

Approximate (sundial) time-of-day corresponding to these events can be found by rearranging eq. (2.6):

\(\ \begin{align} t_{U T C}=\dfrac{t_{d}}{C} \cdot\left\{-\lambda_{e} \pm \arccos \left[\dfrac{\sin \phi \cdot \sin \delta_{s}-\sin \Psi}{\cos \phi \cdot \cos \delta_{s}}\right]\right\}\tag{2.8a}\end{align}\)

where the appropriate elevation angle is used from Table 2-2. Where the ± sign appears, use + for sunrise and – for sunset. If any of the answers are negative, add 24 h to the result.

To correct the time for the tilted, elliptical orbit of the earth, use the approximate Equation of Time:

\(\ \begin{align}\Delta t_{a} \approx-a \cdot \sin (M)+b \cdot \sin (2 M+c)\tag{2.8b}\end{align}\)

where a = 7.659 minutes, b = 9.863 minutes, c = 3.588 radians = 205.58°, and where the mean anomaly M from eq. (2.2) varies with day of the year. This time correction is plotted in the Sample Application. The corrected (mechanical-clock) time t_eUTC is:

\(\ \begin{align}t_{e U T C}=t_{U T C}-\Delta t_{a}\tag{2.8c}\end{align}\)

which corrects sundial time to mechanical-clock time. Don’t forget to convert the answer from UTC to your local time zone.

Sample Application(§)

Use a spreadsheet to find the Pacific standard time (PST) for all the events of Table 2-2, for Vancouver, Canada, during 22 Dec, 23 Mar, and 22 Jun.

Find the Answer

Given: Julian dates 355, 82, & 173.

Find: t = ? h (local standard time)

Assume: Pacific time zone: tUTC = t + 8 h.

Use eq. (2.8a) and Table 2-2:

	22Dec	23Mar	22Jun
Morning:	PST (h)
geometric sunrise	8.22	6.20	4.19
apparent sunrise	8.11	6.11	4.09
civil twilight starts	7.49	5.58	3.36
military twilight starts	6.80	4.96	2.32
astron. twilight starts	6.16	4.31	n/a
Evening:
geometric sunset	16.19	18.21	20.22
apparent sunset	16.30	18.30	20.33
civil twilight ends	16.93	18.83	21.05
military twilight ends	17.61	19.45	22.09
astron. twilight ends	18.26	20.10	n/a

Check: Units OK. Physics OK.

Exposition: During the summer solstice (22 June), the sun never gets below –18°. Hence, it is astronomical twilight all night in Vancouver in mid summer.

During June, Vancouver is on daylight time, so the actual local time would be one hour later.

INFO • Astronomical Values for Time

The constants a = 2·e/ω_E , b = [tan²(ε/2)]/ω_E , and c = 2·ϖ in the Equation of Time are based on the following astronomical values: ω_E = 2π/24h = 0.0043633 radians/minute is Earth’s rotation rate about its axis, e = 0.01671 is the eccentricity of Earth’s orbit around the sun, ε = 0.40909 radians = 23.439° is the obliquity (tilt of Earth’s axis), ϖ = 4.9358 radians = 282.8° is the angle (in the direction of Earth’s orbit around the sun) between a line from the sun to the vernal (Spring) equinox and a line drawn from the sun to the moving perihelion (see Figure 2.5, and Figure 21.10 in Chapter 21).

Sample Application (§)

Plot time correction vs. day of the year.

Find the Answer

Given: d = 0 to 365

Find: ∆t_a = ? minutes

Use a spreadsheet. For example, for d = 45 (which is 14 Feb), first use eq. (2.2) find the mean anomaly:

M = 2π·(45-4)/365.25 = 0.705 rad = 40.4°

Then use the Equation of Time (2.8b) in

∆t_a = –(7.659 min)·sin(0.705 rad) + (9.836 min)·sin(2· 0.705 rad + 3.588 rad)

∆t_a = –4.96 – 9.46 = –14.4 minutes

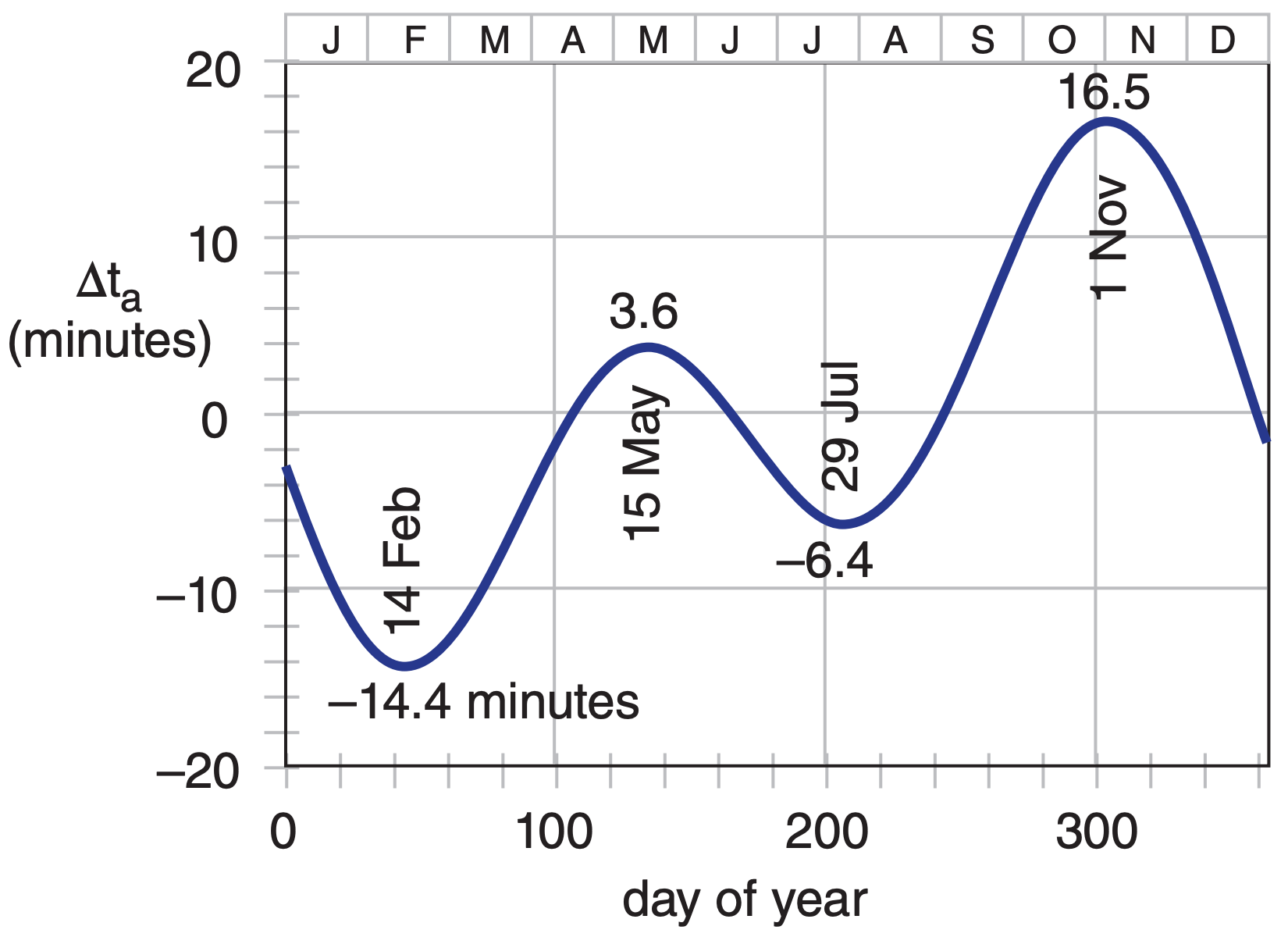
Check: Units OK. Magnitude OK

Exposition: Because of the negative sign in eq. (2.8c), you need to ADD 14.4 minutes to the results of eq. (2.8a) to get the correct sunrise and sunset times.