6.4.7: Pyroxenes

Pyroxenes (Ca,Na,Mg,Fe)(Mg,Fe,Al)(Si,Al)2O6
Most important end members
wollastonite ferrosilite enstatite diopside hedenbergite	Ca2Si2O6 Fe2Si2O6 Mg2Si2O6 CaMgSi2O6 CaFeSi2O6

Pyroxenes contain many different elements, but all pyroxenes have the general formula shown in the blue box. The most common pyroxenes are close to Ca(Mg,Fe)Si₂O₆ or (Mg,Fe)₂Si₂O₆ in composition. So, we can describe the chemistries of most pyroxenes in terms of the five end members listed in the box. The formulas for wollastonite, ferrosilite and enstatite have been written with six oxygen, but they could be written with three. We generally use six to keep formulas consistent with other pyroxenes such as diopside and hedenbergite and also because Ca, Fe, and Mg occupy two distinctly different atomic sites in pyroxenes. Distinguishing the different pyroxene species can be challenging. In the absence of a chemical analysis, black colored pyroxenes are often called augite.

Figure 6.73: Jadeite from California

Figure 6.74: Yellow spodumene from near Sand Diego, California

Some pyroxenes contain minor to appreciable amounts of Na and Al. Na may substitute for Ca, Mg, or Fe. Al can substitute for Ca, Mg, or Fe, and also for Si. An end-member pyroxene, jadeite, has the formula NaAlSi₂O₆. It is found in high-pressure metamorphic rocks and is one of two types of jade that are sometimes prized as gemstones. (The other is an amphibole). Other Na-bearing pyroxenes such as acmite (NaFeSi₂O₆) are found in some igneous rocks. The photo in Figure 6.73 shows a sample of massive green jadeite from central California. It is about 5 cm across.

Li, Cr, and Ti also are sometimes in pyroxene, but are normally minor elements. However, spodumene (LiAlSi₂O₆), is a major mineral in some pegmatites. The photo seen here (Figure 6.74) shows a yellow spodumene crystal about 2 cm tall. Like jadeite, spodumene, especially the lilac-colored variety called kunzite, can be a valuable gemstone.

Figure 6.75: The pyroxene quadrilateral

The ternary diagram in Figure 6.75 is a wollastonite-ferrosilite-enstatite triangle with the important pyroxene end members labeled (enstatite, ferrosilite, diopside, hedenbergite, and wollastonite). The mineral wollastonite, although used as an end member to describe pyroxene compositions, is not a pyroxene. It has a slightly different atomic arrangement and belongs to the pyroxenoid group. (In pyroxenoids, the tetrahedral chains do not zig-zag back and forth as regularly as is shown in Figure 6.70.)

As with the feldspars, we use abbreviations to describe pyroxene compositions. For example, a pyroxene of composition Wo₁₀Fs₈₃En₀₇ is 10% CaSiO₃, 83% FeSiO₃, and 7% MgSiO₃. It has the formula (Ca_0.10Fe_0.83Mg_0.07)SiO₃, equivalent to (Ca_0.20Fe_1.66Mg_0.14)Si₂O₆. This composition is plotted as a dot near the ferrosilite corner of the triangle in Figure 6.75.

We call the lines between end members on ternary diagrams joins. The four-sided polyhedron bounded on the top by the diopside-hedenbergite join, and on the bottom by the enstatite-ferrosilite join, is the pyroxene quadrilateral. It encompasses the compositions of all natural Ca-Mg-Fe pyroxenes.

Natural pyroxenes fall into two main series, distinguished by slightly different atomic arrangements and different crystal shapes: the orthopyroxene series (Opx) and the clinopyroxene series (Cpx). Orthopyroxenes, predominantly solid solutions of the end members ferrosilite and enstatite, have the general formula (Mg,Fe)₂Si₂O₆. The photo on the left below (Figure 6.76) shows green enstatite crystals (orthopyroxene) in a volcanic rock from near Crater Lake National Park, Oregon. Natural orthopyroxenes often contain small amounts of CaSiO₃. So, their compositions do not plot on the bottom of the quadrilateral, but slightly above.

Figure 6.67: 2 mm long green crystals of enstatite from Summit Rock, Oregon

Figure 6.77: Green diopside with white calcite in a marble from the Adirondack Mountains, New York

The photo on the right above (Figure 6.77) shows an example of clinopyroxene, green diopside crystals in a metamorphosed limestone. Most clinopyroxene, is predominantly a solution of diopside and hedenbergite, and so has the general formula Ca(Mg,Fe)Si₂O₆. But natural pyroxenes may be somewhat deficient in CaSiO₃. This give them a composition that does not plot on the diopside-hedenbergite join but, instead, plots within the pyroxene quadrilateral. A less common kind of clinopyroxene, pigeonite, has composition close to orthopyroxene. No pyroxenes have compositions more calcic than diopside or hedenbergite because Ca is limited to only the larger two of the four sites between the tetrahedral chains in pyroxenes.

Figure 6.78: Black augite crystals from Muhabura Volcano, Rwanda

We call pyroxenes with compositions that plot within the quadrilateral augite, subcalcic augite, or pigeonite (see Figure 6.75) depending on their composition. Augite and subcalcic augite are clinopyroxenes with Ca : (Mg + Fe) ratios less than 1. Pigeonites, first found at Pigeon Point, Minnesota, are very high-temperature pyroxenes that only form in quickly cooled volcanic rocks. Figure 6.78 shows an example of large black augite crystals.

Because orthopyroxenes and clinopyroxenes have slightly different atomic arrangements there is a complex solvus between them. At high temperatures, intermediate composition pyroxenes – those that plot within the quadrilateral can be stable. At low temperatures most of the pyroxene quadrilateral is taken up by a large miscibility gap, so intermediate composition pyroxenes are unstable.

Figure 6.79: The large miscibility gap in the pyroxene quadrilateral at 800 ̊C, 1 atm

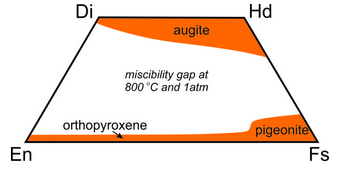
Figure 6.79 shows the gap (in white) at 800 ̊C. Because of this gap, homogeneous pyroxenes with intermediate compositions are only found in some rare high-temperature rocks. At lower temperatures they tend to “unmix.” Analogous to the feldspars, a homogeneous high-temperature pyroxene of intermediate composition may become unstable and separate into two pyroxenes at low temperature. This sometimes leads to exsolution and textures similar to perthitic feldspars.

Figure 6.80: Microscope view of exsolution in a pyroxene grain. Field of view is 2mm across

The photo in Figure 6.80, taken through the lens of a petrographic microscope, shows exsolution in pyroxene. The colors are artifacts and not the true color of the minerals. An original pyroxene (subcalcic augite) unmixed upon cooling, producing exsolution lamellae (the stripes) and the texture we see here. The blue-red lamellae are clinopyroxene and the light colored lamellae are orthopyroxene. The compositions of both lamellae depend on the temperature at which exsolution occurred (Box 6-4). So, the compositions of exsolved pyroxene (and feldspar) lamellae are sometimes used as geothermometers to learn the temperature at which a rock equilibrated.

Diopside-Enstatite Solvus and Geothermometry

The miscibility gap between orthopyroxene (Opx) and clinopyroxene (Cpx) is sometimes used to calculate the temperature at which igneous or metamorphic rocks formed. Petrologists call such mineral systems geothermometers. Geothermometers are based on a fundamental consequence of thermodynamics: at high temperatures, solid-solution minerals may have intermediate compositions, but at low temperatures many solid solutions unmix so that compositions are relatively close to end members. Figure 6.80 (above) shows an example of a single pyroxene grain that has unmixed to become two pyroxenes.

Figure 6.81: The miscibility gap and solvus for Mg-Ca pyroxenes

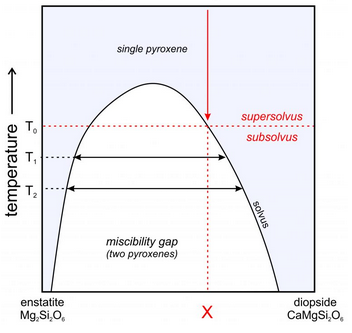
Figure 6.81 is a schematic showing the Opx-Cpx gap between enstatite and diopside. The gap narrows at high temperature and does not extend to the very high temperatures where magmas crystallize and pyroxenes first form. Consequently, pyroxenes of any composition can crystallize from a magma. But, with cooling, many pyroxenes will unmix, producing compositions closer to end member enstatite and diopside than the original pyroxene.

A pyroxene of composition X will be stable at temperatures above T₀, but if it crystallizes or equilibrates at lower temperature, it will unmix to form two pyroxenes. So, as temperature decreases from supersolvus to subsolvus (at T₀), unmixing will produce separate grains of Opx and Cpx in the same rock, or it may produce single grains of pyroxene containing blebs (small inclusions with exsolved compositions in a larger host) or exsolution lamellae of different compositions. As temperature decreases from T₀ to T₁ to T₂, the coexisting pyroxenes will become closer to end member enstatite and diopside. By analyzing the compositions of coexisting Opx and Cpx, petrologists can estimate the temperature of equilibration.

Pyroxenes are not the only minerals that can be used as geothermometers. Feldspars, carbonates, and others can serve the same purpose. Geothermometry is not, however, always simple or straightforward. Many things besides temperature affect the compositions of coexisting minerals. Among others, petrologists must be concerned with the effects of pressure, of minor elements in minerals, and of disequilibrium.