Skip to main content
Geosciences LibreTexts

8.9: Reading- Body Waves

  1. Last updated
  2. Save as PDF
  • Page ID
    11509

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Body waves travel through the interior of the earth. There are two types of body waves: P-waves and S-waves.

    P-Waves

    The P in P-waves stands for primary, because these are the fastest seismic waves and are the first to be detected once an earthquake has occurred. P-waves travel through the earth’s interior many times faster than the speed of a jet airplane, taking only a few minutes to travel across the earth.

    P-waves are predominantly compressional waves. As a P-wave passes, material compresses in the same direction the wave is moving, and then extends back to its original thickness once the wave has passed. The speed at which P-waves travel through material is determined by:

    • rigidity—how strongly the material resists being bent sideways and is able to straighten itself out once the shearing force has passed – the more rigid the material, the faster the P-waves
    • compressibility—how much the material can be compressed into a smaller volume and then recover its previous volume once the compressing force has passed; the more compressible the material, the faster the P-waves
    • density—how much mass the material contains in a unit of volume; the greater the density of the material, the slower the P-waves

    The animations below show P-waves propagating across a plane (left) and from a point source (right).

    animation of a compression wave across a plane animation of a compression wave emanating from a point in the center of a plane

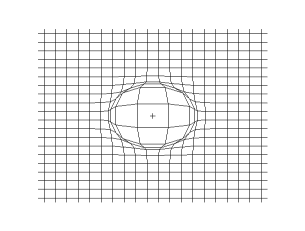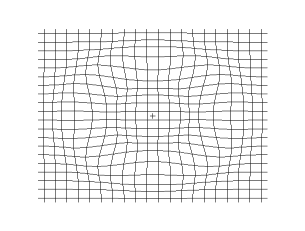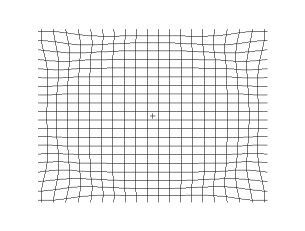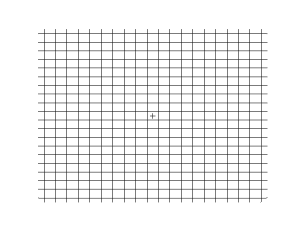
    P-waves travel through liquids and gases as well as through solids. Although liquids and gases have zero rigidity, they have compressibility, which enables them to transmit P-waves. Sound waves are P-waves moving through the air.

    Because the earth’s mantle becomes more rigid and compressible as the depth below the asthenosphere increases, P-waves travel faster as they go deeper in the mantle. The density of the mantle also increases with depth below the asthenosphere. The higher density reduces the speed of seismic waves. However, the effects of increased rigidity and compressibility in the deep mantle are much greater than the effect of the increased density.

    P-waves travel through materials with rigidity and/or compressiblity, and density
    greater rigidity faster P-waves
    greater compressibility faster P-waves
    greater density slower P-waves

    S-Waves

    The S in S-waves stands for secondary, because they are the second-fastest seismic waves and the second type to be detected once an earthquake has occurred. Although S-waves are slower than P-waves, they still travel fast, over half the speed of P-waves, moving at thousands of kilometers per hour through the earth’s crust and mantle.

    S-waves are shear waves (though that is not what the S stands for). They move by material flexing or deforming sideways (shearing) from the direction of wave travel, and then returning to the original shape once the wave passes. The speed at which S-waves travel through material is determined only by:

    • rigidity — how strongly the material resists being bent sideways and is able to straighten itself out once the shearing force has passed – the more rigid the material, the faster the S-waves
    • density — how much mass the material contains in a unit of volume – the greater the density of the material, the slower the S-waves

    The animations below show S-waves propogating across a plane (left) and from a point source (right):

    animation of a shear wave across a plane animation of a shear wave emanating from a point in the center of a plane

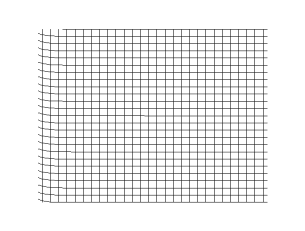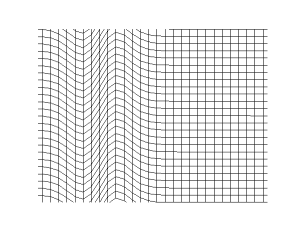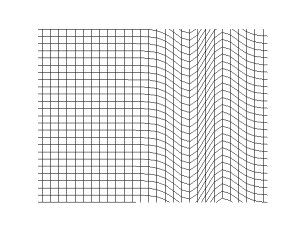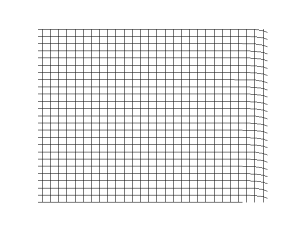
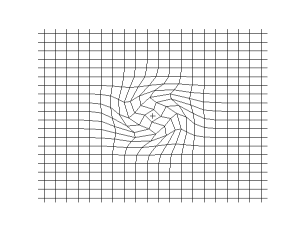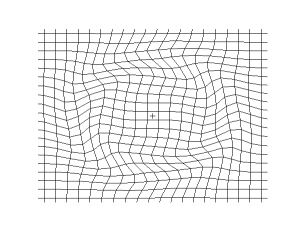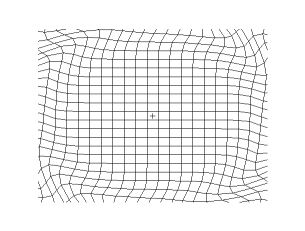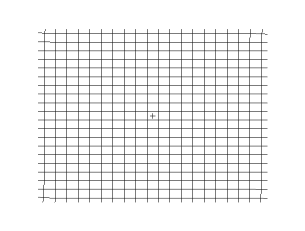
    S-waves can travel only through solids, because only solids have rigidity. S-waves cannot travel through liquids or gases.

    Because the earth’s mantle becomes more rigid as its depth below the asthenosphere increases, S-waves travel faster as they go deeper in the mantle. The density of the mantle also increases at greater depth, which has the effect of reducing the speed of seismic waves, but the increase in rigidity is much greater than the increase in density, so S-waves speed up as they get deeper in the mantle, in spite of the increased density.

    S-waves travel through materials with rigidity and density
    greater rigidity faster S-waves
    greater density slower S-waves

    Contributors and Attributions

    CC licensed content, Shared previously

    This page titled 8.9: Reading- Body Waves is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Lumen Learning via source content that was edited to the style and standards of the LibreTexts platform.