2A: Normal Faults
- Page ID
- 1336
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)On normal faults, the hanging wall has moved down relative to the foot wall. These faults are generally steeply dipping, with a dip angle of 60° or greater. Low-angle normal faults have a dip of below 45°, accomplishing more extension per unit slip. How these faults are able to form and slip at such a low angle is a mechanical mystery.
Structures Formed by Normal Faults
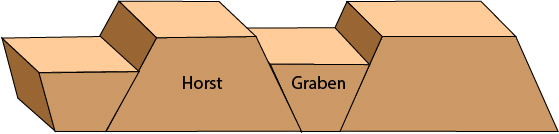
A horst is an upthrown block between oppositely dipping normal faults. A graben is a downthrown block between oppositely dipping normal faults.
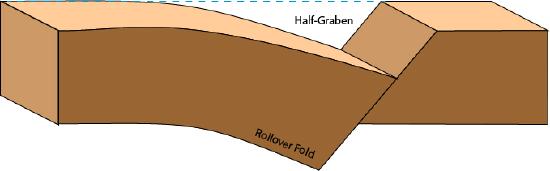
A half-graben is the tilted hanging wall basin of a normal fault.
Large faults are often associated with smaller, secondary faults. When these faults dip in the same direction as the main fault, they are synthetic faults, and when oppositely-dipping, they are called antithetic faults.
Extension, Reconstruction, and Balancing Problems
The amount of extension is the length gained in a region. Extension strain, also known as elongation strain, is the change in length of a region divided by the original length:
\[e= \frac{\Delta L}{L_{0}}\]
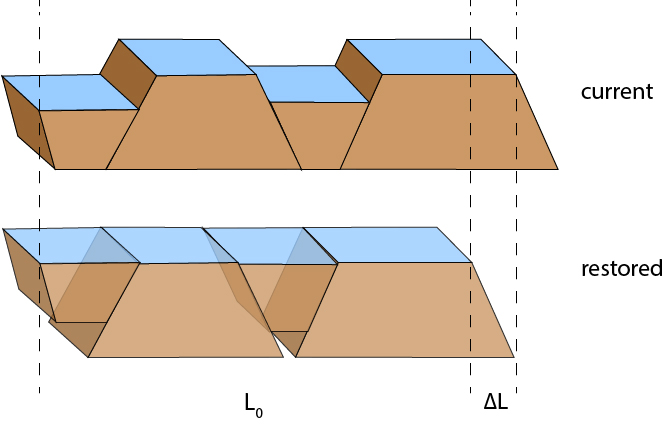
Reconstruction of an originally planar, horizontal marker is a straightforward way to measure extension and extension strain. Simple reconstructions like these, however, are not always possible geologically. Balancing a graben, for example, is challenging without producing gaps or overlaps.
In practice, faults bounding grabens may change angles or become damage zones instead of single simple planes, and rocks may undergo significant breakup to fill in spaces.
Listric Normal Faults
Listric normal faults have decreasing dip with depth. Slip causes tilting in the hanging wall, resulting in a rollover fold.

Listric fault surfaces often have irregular, strongly curved fault corrugations, also called mega-mullions, which indicate the slip (down-dip) direction. Similarly to grabens, listric normal faults balance poorly without other structures eliminating gaps at the fault plane or in the hanging wall:
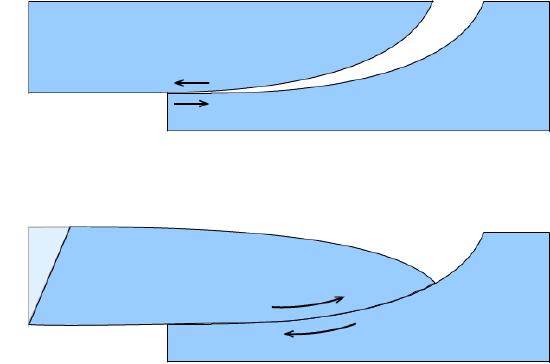
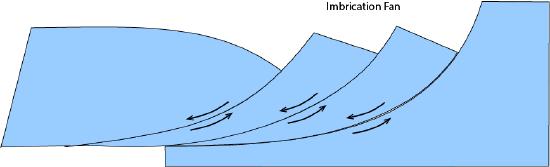
If the magnitude of extension is small, imbricate listric faults can accommodate extension, forming an imbrication fan to prevent gaps.
If extension is great, the same problems with gap formation develop in the block with the rollover fold, regardless of the presence of an imbrication fan. Greater extension strain thus requires antithetic or synthetic domino faulting in the hanging wall, where slip on imbricate faults allows rotation and avoids gap formation.
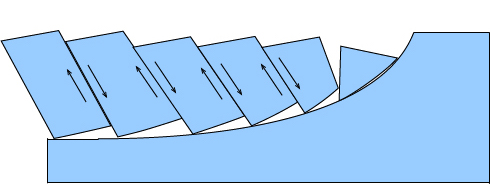
Once a large amount of rotation has occurred by domino faulting, a new set of steeply dipping imbricate faults may form and slip will be continued along these.
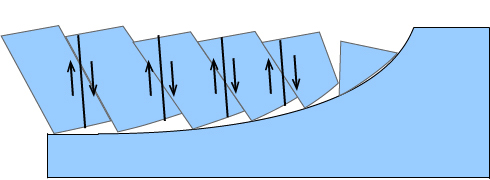
Detachment Faults
Large offset on a listric normal fault may juxtapose mid-crustal rocks against basin sediments. When this occurs, the fault is called a detachment or detachment fault. The hanging wall of a detachment fault is known as the upper plate, and the foot wall as the lower plate.

As extension is accomplished, removal of the hanging wall load on the foot wall causes isostatic uplift of the foot wall. This may result in doming of the fault plane and exposure in a basement window of metamorphosed foot wall rocks, called a metamorphic core complex. Fault plane corrugations are often visible on the fault surface where exposed in a basement window.
Normal Fault Zone Features
An accommodation zone is a region between faults that accomplishes deformation in a more distributed fashion. This term applies equally well to all fault types, but the geometry of these zones is often best expressed in areas of normal faulting, especially when a deformed marker, such as a lava flow, is preserved over a wide region. Common accommodation zone features include relay ramps, which form between two en echelon normal faults, and transfer faults, which are strike-slip faults linking two dip-slip faults.

This image shows the Hat Creek Fault cutting basalt flows of the Modoc Plateau in northeastern California. Multiple scales of relay faulting are visible here; some relay ramps have been cut by subsequent generations of faulting.
Normal faulting can create basins that fill in with sediment as the fault slips. This leads to a characteristic fanning geometry of sedimentary layering, with strata increasing in thickness toward the foot wall. The process which creates these growth strata is called growth faulting.
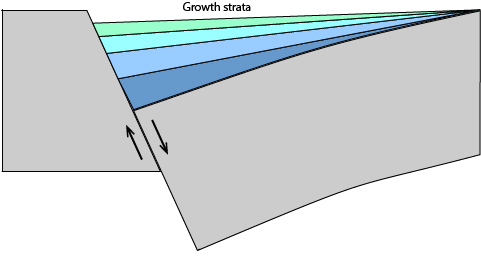
Deeper strata have greater offsets and more tilting, as they have been subject to motion on the fault plane for a longer period of time. Systematic changes in sedimentary rock type are also frequent in these basins. Transfer zones commonly create small topographic lows, which become significant channels for sediment input to the hanging wall basin.
In zones of rifting, the main rift-bounding faults may change orientation, or rift polarity. This is common in rift valley lakes in East Africa.

Summary
List of Terms
- Normal fault
- Low-angle normal fault
- Horst
- Graben
- Half-graben
- Antithetic fault
- Synthetic fault
- Extension
- Extension strain
- Elongation strain
- Listric fault
- Rollover fold
- Fault corrugation
- Mega-mullion
- Imbricate faults
- Imbrication fan
- Domino faulting
- Detachment
- Basement window
- Metamorphic core complex
- Accommodation zone
- Relay ramp
- Transfer fault
- Growth strata
- Growth faulting
- Rift polarity
Contributors
Michael E. Oskin (Department of Earth and Planetary Sciences, UC Davis)