11.3: Saltation II
- Page ID
- 4220
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Effect of Saltation on the Velocity Profile of the Wind
You have seen that the air exerts a drag force on the saltating particles as they rise from the bed. Conversely, the equal and opposite force exerted by the particles on the wind tends to slow the wind. Given the commonly substantial concentration of particles in the saltation layer, you should expect the structure of the wind in the saltation layer to be different from that in the absence of saltation. At first thought, you might assume that there is a kind of symmetry at work here: perhaps the particles tend accordingly to speed up the wind as they descend from the tops of their trajectories down into region of lower wind speed. If, however, our earlier deduction to the effect that the particles have not yet been fully accelerated by the wind even when they reach the ends of their trajectories is true, then the saltating particles must be responsible for a net decrease in wind velocity. You will see below that this is indeed the case.
As with so many aspects of eolian saltation, Bagnold was the first to give systematic attention to the effect of saltation on wind velocity. Bagnold (1941), and many later researchers, have measured wind-velocity profiles in the presence of saltation. Figure \(\PageIndex{1}\), taken directly from Bagnold’s book, shows actual measurements.
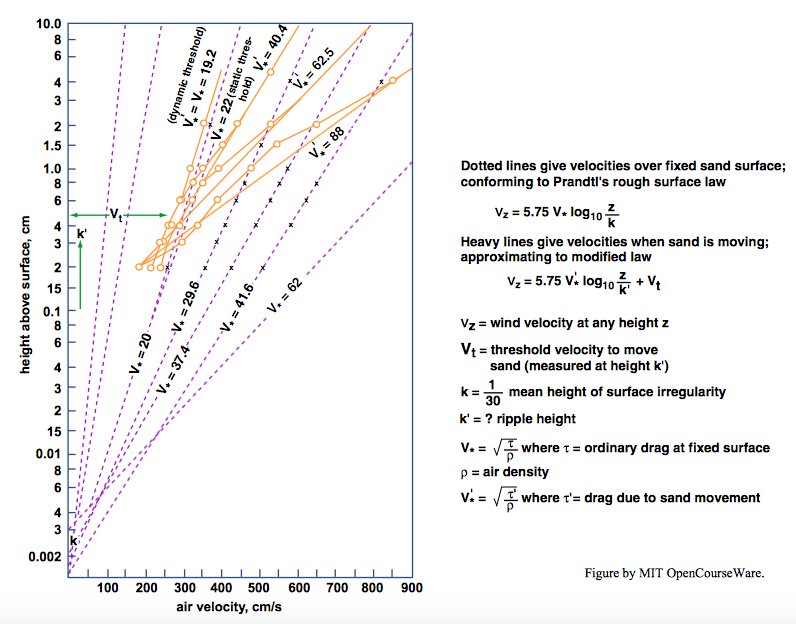
Recall from Chapter 4 that the air speed over a fixed rough bed varies logarithmically with height above the bed, according to the law of the wall for rough boundaries (Equation 4.7.22, reproduced here as Equation \ref{11.1}, for your convenience):
\[\frac{\overline{u}}{u_{*}}=A \ln \frac{y}{y_{0}} \label{11.1} \]
where \(y_{0}\), the roughness length, is nothing more than a convenience variable to put the law of the wall as expressed in the form of Equation 4.7.20 into a neater form. The roughness length \(y_{0}\) has the property that when the profile expressed by Equation \ref{11.1} is extrapolated downward, its intercept with the \(\overline{u} / u_{*}\) axis (nominally, zero wind velocity) is at a value of \(y\), the height above the bed, of \(D/30\) for close-packed granular roughness—but in reality Equation \ref{11.1} ceases to hold at heights above the bed not much greater than the particle diameter, as discussed in Chapter 4.
In a dimensional plot of wind speed u against height y above the sand bed, if \(u_{*}\) is changed, the slope of the velocity profile varies, but the intercept \(y_{0}\) does not, according to Equation \ref{11.1} (see Figure \(\PageIndex{2}\), an idealization of Figure \(\PageIndex{1}\)). What Figure \(\PageIndex{2}\) shows is that when a saltation layer is present the profile of wind speed in the region above the saltation layer is still logarithmic, but with a significant modification: profiles for different shear velocities no longer converge on the point \((0,y_{0})\) located on the \(y\) axis (where \(u = 0\)) but, approximately, on a point (\(u_{o}^{\prime}, y_{0}^{\prime}\)), where \(u_{0}^{\prime}\) is not equal to zero and \(y_{0}^{\prime}\) is much larger than \(y_{0}\). The effect on the velocity profile above the saltation layer is the same as if the roughness of the bed had been increased— as if, in Equation 4.7.20 or 4.7.21 the size of the roughness elements, \(D\), had been increased. The saltation layer thus adds resistance to the wind, as we deduced at the beginning of this section.
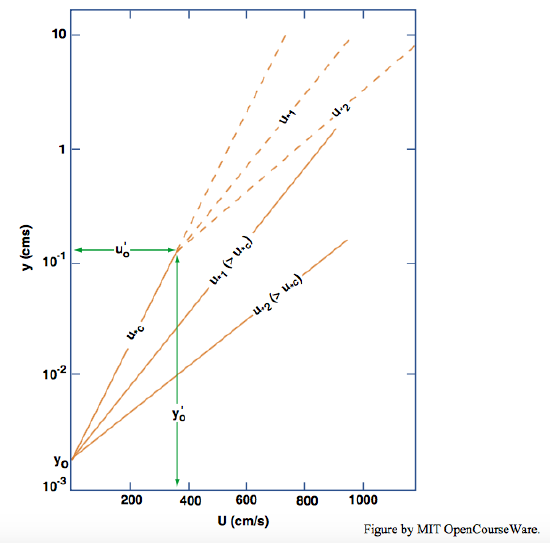
The question then arises: how low does the wind speed become, deep in the saltation layer, just above the tops of the bed particles? Owen (1964) offered the following hypothesis, noted in an earlier section: the shear stress exerted by the wind on the sand bed is just sufficient to maintain the surface particles in a mobile state—which is much lower than would be the case with the same sand bed and with the same overlying wind but with the bed particle immovable.
Jump-Distance Distribution
The downwind distance traversed by saltating particles ranges from very short, perhaps of the order of a few millimeters (the minimum saltation distance is partly a matter of semantics, hinging upon one’s view of the transition from particle movement in surface creep to particle movement in saltation) to very long, as much as several meters in strong winds under which the saltation layer extends upward by more than a meter. When the flights of a large number of saltating particles in a uniform wind are considered, there is some well defined probability distribution of jump distances.
Measuring the jump-distance frequency distribution is not straightforward. Direct measurement of jump distances, by means of tracking trajectories photographically, is likely to be biased toward the longer trajectories, owing to the greater particle concentrations at lower levels, which tend to obscure the individual trajectories, and the slower particle speeds, which makes measurements of speeds from photographic images more difficult. The few attempts at measurement have exploited the indirect method of measuring the catch of particles in long bed-level traps of various designs (Kawamura, 1951; Horikawa and Shen, 1960; Belly, 1964).
It is not difficult to show that the jump-distance distribution is related to the distribution of catch in a horizontal sand trap by
\[f(\eta)=\frac{1}{G o} \frac{d G}{d x} \label{11.2} \]
(Kawamura, 1951), where \(f(\eta)\) is the frequency distribution of saltation jump distances \(\eta\), \(G\) is the saltation catch (mass per unit area and unit time) in a horizontal trap with leading edge at \(x = 0\) and extending downwind in the positive \(x\) direction, and \(G_{\text{O}}\) is the total mass launched into saltation from a unit area in unit time.
The few measurements of jump-distance distribution show three significant features:
- The frequency of jump distances increases monotonically with decreasing jump distance, apparently right up to the transition to surface creep; in other words, the maximum of the curve is at very small, or even zero, jump distance.
- The mean jump distance is significantly greater than the spacing of the wind ripples over which the saltation takes place.
- There is no well-defined maximum jump distance, as is to be expected, given the gradually decreasing concentration of saltating particles with height, but the frequency of jump distances several meters long is not negligible.
Mass-balance considerations in the context of jump-distance distributions are enlightening. Think about saltation that is uniform, in the sense that the picture of saltation is exactly the same at every point along the wind direction. Uniform saltation is very closely approximated where a sand-moving wind blows steadily over a level sand surface of great extent. In uniform saltation, the mass of particles launched from a small unit area of the bed must be equal to the mass of particles arriving onto that area—and, more specifically, the jump-distance distributions of both the incoming and outgoing particles must be identical, or the saltation would not be uniform. This is a demanding requirement, because each incoming particle gives rise to zero, one, or more outgoing particle motions with jump distances not likely to be identical to its own. Nature somehow manages to adjust the jump-distance distribution of outgoing particles to be the same as that of the incoming particles. There must be a self-regulating mechanism at work: if not enough downwind transport is engendered from the unit area by the incoming particles, the intensity of saltation falls off downwind until what leaves matches what arrives, and if the incoming particles cause an even greater transport rate out of the area, the saltation transport rate increases until the rate becomes uniform. This transformation of incoming saltation to outgoing saltation can be described in terms of what Werner (1990) calls the splash function. The following makes these matters more concrete.
In eolian saltation the mass of moving particles that make contact with a small reference area on the bed includes particles launched into saltation from a range of distances upwind, from only a fraction of a particle diameter, in the case of the surface creep, to as much as a few meters, in the case of the highest-flying particles in saltation. With \(x\) as incoming jump length, let the function \(g_{in}(x)\) represent the jump-distance distribution of this incoming mass of particles, expressed as mass per unit bed area per unit time. Similarly, with \(y\) as outgoing jump length the function \(g_{out}(y)\) represents the corresponding jump-distance distribution of the outgoing mass of particles. In uniform saltation, incoming and outgoing mass must be the same for any given jump length, so \(g_{out}\) and \(g_{in}\) are identical distributions. Mathematically this can be expressed as
\[\int_{0}^{\infty} g(x) F(x, y) d x=g(y) \label{11.3} \]
Where \(F(x, y)\) is the splash function of Werner (1990). Equation \ref{11.3} is an integral equation—one that contains an integral. A function with the form of \(F\) in Equation \ref{11.3} is said to be the kernel of the equation. In this case, a mathematician might call \(F\) a self-replicating kernel function, because it has the remarkable property of transforming the other factor in the integral on the left, \(g(x)\), into an identical function, \(g(y)\), on the right.
The requirement, mentioned above, that in uniform saltation the jump-distance distributions become adjusted so that the incoming and outgoing jump-distance distributions, \(g_{in}\) and \(g_{out}\), are identical and a function of the wind strength can be expressed in the context of Equation \ref{11.3} as follows. For each value of incoming jump distance \(x\), the splash function acts on the incoming mass of saltating particles to give a contribution to the mass distribution of outgoing jump distance, and the sum of all of these contributions is the outgoing mass distribution of jump distances.
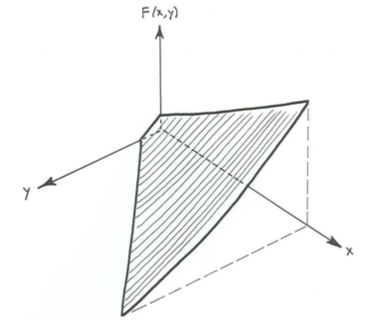
What can we say, qualitatively, about the nature of the splash function \(F\)?
- The momentum of incoming particles, and therefore their ability to set particles in motion at any given outgoing jump distance, increases with increasing incoming jump distance, so \(F\) should be a monotonically increasing function of \(x\) at constant \(y\) for all \(y\), including \(y = 0\).
- The mass of particles set in motion by arrival of particles with a given jump distance \(x\) should be greater for smaller outgoing jump distances than for larger, so \(F\) should be a monotonically decreasing function of \(y\) for constant \(x\).
- Incoming particles with very small jump distances can give rise to only a narrow range of jump distances, and therefore relatively small momentum, not much larger than their own, whereas incoming particles with very large jump distances, and therefore relatively large momentum, can give rise to a wide range of outgoing jump distances from very small to even larger than their own, so the overall rate of decrease of \(F\) with increasing \(y\) at constant \(x\) should be sharpest for very small \(x\) and become gentler with increasing \(x\).
- \(F\) must approach zero as \(x\) approaches zero, because the mass of particles mobilized must go to zero as the incoming jump distance, and therefore the momentum of the incoming particles, goes to zero.
Figure \(\PageIndex{3}\) shows, qualitatively, what the splash function F might actually look like.
Saltation Transport Rates
It was mentioned in the section on saltation heights that the concentration of saltating particles tails off gradually upward. This is known from sampling to measure the transport rate of saltating particles. Such measurement is simple in principle but somewhat troublesome in actual practice. The common procedure is to install, on a vertical shaft or frame in the sand, a series of particle-catching devices, which are uncovered for a fixed time and then the mass of particles caught in each is measured. A curve of catch versus height is plotted, and the total transport rate is the integral of that curve from the bed to a level above the highest saltation heights. Once the transport at any given level is known, the concentration of the saltating particles at that level can be found if the time-average wind speed is measured at the same level at the same time, inasmuch as the transport rate must equal the concentration times the speed of passage of the parcel of air that contains the particles. Systematic measurements of transport rate date from the time of Bagnold (1941); see also the early and widely cited work of Williams (1964).
One practical problem is that any such catching devices, no matter how well designed, inevitably disturb the passing wind to some extent, and even aside from that, measurements near the sand bed, where the mass flux of particle is greatest, is difficult to arrange. In recent years, high-resolution measurements using non-intrusive optical sensors have been developed (e.g., Butterfield, 1999), thus mitigating some of the problems. Another problem is that it is not easy to measure the transport rate of sediment moved as surface creep.
A more general problem, however, has to do with what is actually being measured. The wind is gusty on natural sand surfaces. Even on a broad, horizontal sand- coved plain, the large-scale eddy structure in the lowermost atmosphere means that the saltation catch varies with time on periods of seconds to many minutes. The problem is exacerbated on the upwind flanks of sand dunes, owing to the strong wake produced by an upwind dune. A catch averaged over many minutes may be very different from an “instantaneous” measurement, taken over a number of seconds. This problem could be circumvented in a wind tunnel, but the tunnel would have to be large enough that the saltation profile is fully developed vertically even in very strong winds. Few wind tunnels are of such a size.
Saltation in Unsteady Winds
In recent years, increasing attention has been given to how the saltation cloud adjusts to changing wind conditions, given that winds in the outdoors are characteristically highly variable, on time scales of minutes to hours. The problem can be posed as follows. A surface of loose sand lies susceptible to saltation. A strong gust of wind initiates saltation. How do the conditions of saltation respond? The saltating cloud responds rapidly. The response of the saltation to the changing wind speed has been studied in wind tunnels and in the field (e.g., Butterfield, 1991, 1998) (Figure \(\PageIndex{4}\)), and several numerical models have been developed to account for the observations (e.g., Anderson and Haff, 1991; McEwan and Willetts, 1991; Spies and McEwan, 2000; Spies et al., 2000). In numerical simulations by Spies and McEwan (2000), you can see how the transport rate develops in time and space: at a given time after onset of the wind, the transport rate reaches a maximum near the upstream edge of the sand bed, and the maximum in transport rate moves downstream with time.

One significant aspect of the response of saltation to a sudden increase in wind speed, from below threshold to well above, is that the saltation transport rate first increases but then decreases somewhat before settling into equilibrium with the wind. The reason is easy to understand: it takes some time for the effect of theft of fluid momentum on the part of the saltating particles to develop—so there is a brief period of time during which the aerodynamic forces on bed particles has not decreased significantly, while the impact forces exerted by saltating particles on the bed have already become significant. As the wind adjusts in such a way as to exert a smaller bed shear stress (see the earlier section), the saltation cloud settles down to a state of somewhat less vigorous saltation. There is thus a transient maximum in saltation transport at the outset of a transport event. Spies et al. (2000) have done numerical simulations of this effect.
The Transition from Saltation to Suspension
You learned way back in Chapter 3 that the characteristic fluctuations in velocity in a turbulent flow are a certain small percentage of the mean velocity. Because of that, the characteristic vertical fluctuating velocity in near-surface winds should increase with wind speed. If those vertical velocities are sufficiently large, even saltating sand particles are affected in the trajectories by the fluctuations. Likewise, in a wind with a given speed, the effect of the velocity fluctuations on particle trajectories increases with decreasing particle size.
The transition from classic saltation trajectories to trajectories that are non-negligibly affected by turbulence is an area of study in eolian sedimentation that has less attention than the study of saltation. A distinction needs to be made here between
- fine particles (usually referred to in the eolian literature as dust), which are raised either directly by the wind or indirectly by the impact of saltating larger particles on exposed surfaces of sediment or bedrock, and which go directly into true suspension even at wind speeds for which vertical fluctuating turbulent velocities are much lower than the settling velocities of the coarser saltating particles, and
- sand particles moved by winds so strong that the vertical fluctuating velocities become comparable to the settling velocities of the particles, causing particle trajectories to show at least some influence of turbulence.
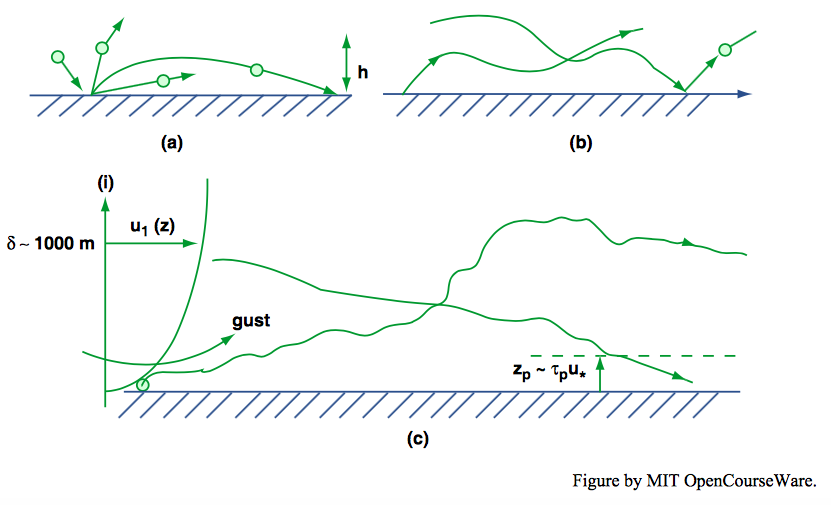
Nishimura and Hunt (2000) found, in a wind-tunnel study of particle trajectories, that the transition from saltation to suspension begins to be noticeable when the shear velocity is still as low as one-tenth the particle settling velocity. As wind speeds increase beyond that, particle trajectories show greater and greater irregularity due to interaction with turbulent eddies (Figure \(\PageIndex{5}\)).
Models of Eolian Saltation
After the early work of Reizes (1978), and concurrently with the development and elaboration of the concept of the splash function by Werner and co-workers, the focus of studies of eolian saltation began to shift toward modeling of eolian sediment transport as a unified phenomenon with saltation dynamics as the basis (e.g., Anderson and Hallet, 1986; Ungar and Haff, 1987; Anderson and Haff, 1988; Werner and Haff, 1988; Werner, 1990; Haff and Anderson, 1993). As time has gone on since the late 1980s, with the development of ever greater computing power, numerical models of eolian transport have become more and more able to simulate the physics of saltation and the consequences for eolian sediment flux.
Models at first aimed at simulating saltation transport in steady and fully developed winds, of the kind that can be produced without difficulty in a long wind tunnel (e.g., McEwan and Willets, 1991, 1993a, 1993b; Willetts, 1998). More recent models have moved on to simulation of unsteady winds—for example, a saltation event in which a sudden strong wind gust generates a cloud of saltating particles, which develops in time and with downwind distance, as described in an earlier section (e.g., Spies and McEwan, 2000; Spies et al, 2000).
Sand Movement on Mars and Venus
Look back at Figure 8.1.5, in Chapter 8, to remind yourself that the case of sand transport by wind on the Earth’s surface is only one point in the wide range of density ratios for which solid particles are transported by fluid flows. The density ratio for sand movement on Mars (if we assume that the mineral particles available on the Martian surface are not greatly different in density from those on the surface of the Earth) lies even farther to the right along the \(\rho_{s}/\rho\) axis than the density ratio for eolian sediment transport on Earth. In contrast, the Venus case lies not much farther to the right than the case of transport of ultra-heavy minerals (gold being the obviously important example) by water flows on the Earth’s surface! It seems fair to say that the great bulk of the research so far on transport of loose particulate sediment on Mars and Venus has come from the research group headed by R. Greeley, and especially on the part of J.D. Iversen and of B.R. White (Greeley et al., 1974; Greeley et al., 1976; Iversen et al., 1975; Iversen et al. 1976a; Iversen et al. 1976b; Iversen et al. 1976c; White, 1979; Iversen and White, 1982; White et al., 1987) as well as more recent contributions (e.g., Fenton and Bandfield, 2003; Bourke et al., 2004). Much of the data and conclusions from the work of Greeley’s group is presented in the book by Greeley and Iversen (1985). The emphasis in these notes is on eolian sand movement on Mars, in light of the spectacular recent advances in our understanding, and the much enhanced interest, that have arisen from the Rover results.
A first-order and seemingly unassailable deduction we can make at the outset is that saltation should be the dominant mode of movement of sand-size particles on Mars—because the relative inertia of the particles is even greater than in eolian transport on Earth. In the case of Venus, for which the density ratio is greater than for sand in water on Earth by not much more than one order of magnitude, particle trajectories are much more likely to be affected by the turbulence in the wind than is the case for saltation on Mars.
Look back to the discussion of the effect of density ratio on thresholds, in Chapter 9, to see that in terms of the Shields diagram, in which the threshold for sediment motion is expressed in terms of the Shields parameter and the particle Reynolds number, the difference between dimensionless threshold for mineral particles in water and for mineral particles in air is not entirely clear (to me, at least). Given the great differences in atmospheric density between Earth and Mars, as well as the difference in gravity, you should expect that when expressed in dimensional terms the thresholds should be quite different. Figure \(\PageIndex{6}\) shows a comparison of motion thresholds expressed in terms of the shear velocity of the wind.
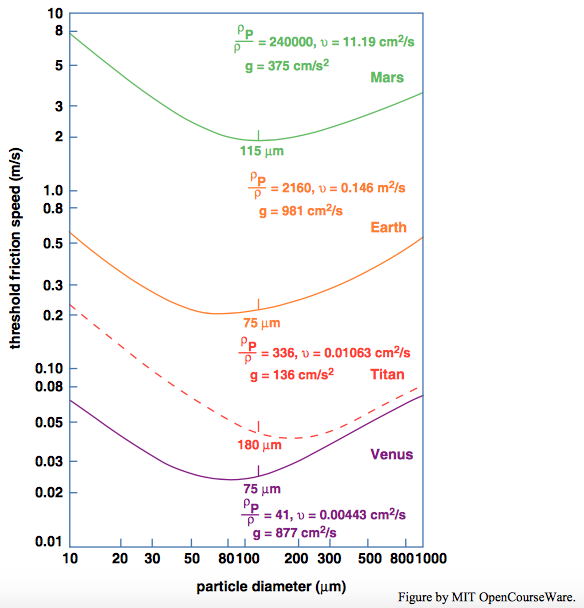
It seems clear that saltation jump heights and lengths must be much greater on Mars than on Earth, owing to the greater wind speeds and lesser gravity. Another significant deduction we can make is that because of the much greater wind speeds on Mars, together with the even greater relative inertia of the particles, the destructive effects of impacts of saltating mineral particles on rock surfaces should be even greater on Mars than on Earth.
References Cited Chapter 11
Anderson, R.S., 1989, Saltation of sand: a qualitative review with biological analogy: Royal Society (London), Proceedings, v. B96, p. 149-165.
Anderson, R.S, and Haff, P.K., 1988, Simulation of eolian saltation: Science, v. 241, p. 820-823.
Anderson, R.S., and Haff, P.K., 1991, Wind modification and bed response during saltation of sand in air, in Barndorff-Nielsen O.E., and Willetts, B.B., eds., Aeolian Grain Transport 1; Mechanics: Acta Mechanica, Supplementum 1, Springer-Verlag, p. 21-51.
Anderson, R.S., and Hallet, B., 1986, Sediment transport by wind: Toward a general model: Geological Society of America, Bulletin, v. 97, p. 523-535.
Anderson, R.S., Sørensen, M., and Willetts, B.B., 1991, A review of recent progress in our understanding of aeolian sediment transport, in Barndorff-Nielsen O.E., and Willetts, B.B., eds., Aeolian Grain Transport 1; Mechanics: Acta Mechanica, Supplementum 1, Springer-Verlag, p. 1-19.
Bagnold, R.A., 1941, The Physics of Blown Sand and Desert Dunes: Chapman & Hall, 265 p.
Belly, P.Y., 1964, Sand Movement by Wind: US Army, Corps of Engineers, Coastal Engineering Research center, Technical Memorandum 1, 38 p.
Bourke, M.C., Bullard, J.E., and Barnouin-Jha, O.S., 2004, Aeolian sediment transport pathways and aerodynamics at troughs on Mars: Journal of Geophysical research, v. 109, E07005, 16 p.
Butterfield, G.R., 1991, Grain transport rates in steady and unsteady turbulent airflows, inBarndorff-Nielsen OE, Willetts BB, eds, Aeolian Grain Transport 1; Mechanics: Acta Mechanica Supplementum 1, Springer-Verlag, p. 97-122.
Butterfield, G.R., 1998, Transitional behaviour of saltation: wind tunnel observations of unsteady winds: Journal of Arid Environments, v. 39, p. 377-394.
Butterfield, G.R., 1999, Near-bed mass flux profiles in aeolian sand transport: high-resolution measurements in a wind tunnel: Earth Surface Processes and Landforms, v. 24, p. 393- 412.
Chepil, W.S., 1945, Dynamics of wind erosion I, Nature of movement of soil by wind: Soil Science, v. 60, p. 305-320.
Chepil, W.S., 1958, The use of evenly spaced hemispheres to evaluate aerodynamic forces on a soil surface: American Geophysical Union, Transactions, v. 39, p. 397-404.
Chepil, W.S., 1959, Equilibrium of soil grains at the threshold of movement by wind: Soil Science Society of America, Proceedings, v. 23, p. 422-428.
Chepil, W.S., 1961, The use of spheres to measure lift and drag on wind-eroded soil grains: Soil Science Society of America, Proceedings, v. 25, p. 343-345.
Einstein, H.A., and El-Samni, E.A. 1949, Hydrodynamic forces on a rough wall: Reviews of Modern Physics, v. 21, p. 520-524.
Fenton, L.K., and Bandfield, J.L., 2003, Aeolian processes in Proctor Crater on Mars: Sedimentary history as analyzed from multiple data sets: Journal of Geophysical research, v. 108 (E12), 5129, 39 p.
Greeley, R., and Iversen, J.D., 1985, Wind As a Geological Process on Earth, Mars, Venus and Titan: Cambridge University Press, 333 p.
Greeley, R., Iversen J.D., Pollack, J.B., Udovich, N., and White, B., 1974, Wind tunnel studies of Martian aeolian processes: Royal Society (London), Proceedings, v. A341, p. 331-360.
Greeley, R., White, B., Leach, R., Iversen, J., and Pollack, J., 1976, Mars: wind friction speeds for particle movement: Geophysical Research Letters, v. 3, p. 417-420.
Haff, P.K., and Anderson, R.S., 1993, Grain scale simulations of loose sedimentary beds: the example of grain–bed impacts in aeolian saltation: Sedimentology, v. 40, p. 175-198.
Horikawa, K., and Shen, H.W., 1960, Sand movement by wind action: US Army, Corps of Engineers, Beach Erosion Board, Technical Memorandum 119, 51 p.
Iversen, J.D., and White, B.R., 1982, Saltation threshold on Earth, Mars and Venus: Sedimentology, v. 29, p. 111-119.
Iversen, J.D., Greeley, R., White, B.R., and Pollack, J.B., 1975, Eolian erosion of the Martian surface, Part 1: erosion rate similitude: Icarus, v. 26, p. 321-331.
Iversen, J.D., Pollack, J.B., Greeley, R., and White, B.R., 1976a, Saltation threshold on Mars: the effect of interparticle force, surface roughness, and low atmospheric density: Icarus, v. 29, p. 381-393.
Iversen, J.D., Greeley, R., and Pollack, J.B., 1976b, Windblown dust on Earth, Mars and Venus: Journal of the Atmospheric Sciences, v. 33, p. 2425-2429.
Iversen, J.D., Greeley, R., White, B.R., and Pollack, J.B., 1976c, The effect of vertical distortion in the modeling of sedimentation phenomena: Martian crater wake streaks: Journal of Geophysical Research, v. 81, p. 4846-4856.
Kawamura, R., 1951, Study of sand movement by wind: University of California, Berkeley, Institute of Engineering Research, Technical Report HEL-2-8, 40 p.
Maegley, W.J., 1976, Saltation and Martian sandstorms: Reviews of Geophysics and Space Physics, v. 14, p. 135-132.
McEwan, I.K., and Willetts, B.B., 1991, Numerical model of the saltation cloud, in Barndorff- Nielsen, O.E., and Willetts, B.B., eds., Aeolian Grain Transport 1; Mechanics: Acta Mechanica, Supplementum 1, Springer-Verlag, p. 53-66.
McEwan, I.K., and Willetts, B.B., 1993a, Sand transport by wind: a review of the current conceptual model, in Pye, K., ed., The Dynamics and Environmental Context of Aeolian Sedimentary Systems: Geological Society of London, Special Publication 72, p. 7-16.
McEwan, I.K., and Willetts, B.B., 1993b, Adaptation of the near-surface wind to the development of sand transport: Journal of Fluid Mechanics, v. 252, p. 99-115.
McGee, W.J., 1908, Outlines of hydrology: Geological Society of America, Bulletin, v. 19, p. 193-220.
Nalpanis, P., Hunt, J.C.R., and Barrett, C.F., 1993, Saltating particles over flat beds: Journal of Fluid Mechanics, v. 251, p. 661-685.
Nickling, W.G., 1988, The initiation of particle movement by wind: Sedimentology, v. 35, p. 499-511.
Nishimura, K., and Hunt, J.C.R., 2000, Saltation and incipient suspension above a flat particle bed below a turbulent boundary layer: Journal of Fluid Mechanics, v. 417, p. 77-102.
Owen, P.R., 1964, Saltation of uniform grains in air: Journal of Fluid Mechanics, v. 20, p. 225- 242.
Reizes, J.A., 1978, Numerical study of continuous saltation: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 104, p. 1305-1321.
Spies, P.J., and McEwan, I.K., 2000, Equilibration of saltation: Earth Surface Processes and Landforms, v. 25, p. 437-453.
Spies, P.J., McEwan, I.K., and Butterfield, G.R., 2000, One-dimensional transitional behaviour in saltation: Earth Surface Processes and Landforms, v. 25, p. 505-518.
Tsuchiya, Y., 1969, Mechanics of the successive saltation of a sand particle on a granular bed in a turbulent stream: Kyoto University, Disaster Prevention Research Institute, Bulletin, v. 19, Part 1, no. 152, p. 31-44.
Tsuchiya, Y., 1970, On the mechanics of saltation of a spherical sand particle in a turbulent stream: Kyoto University, Disaster Prevention Research Institute, Bulletin, v. 19, no. 5, p. 52-57.
Ungar, J.E., and Haff, P.K. 1987, Steady state saltation in air: Sedimentology, v. 34, p. 289-299. Werner, B.T., 1990, A steady-state model of wind-blown sand transport: Journal of Geology, v. 98, p. 1-17.
Werner, B.T., and Haff, P.K., 1988, The impact process in aeolian saltation: two-dimensional simulation: Sedimentology, v. 35, p. 189-196.
White, B.R., 1979, Soil transport by winds on Mars: Journal of Geophysical Research, v. 84, p. 4643-4651.
White, B.R., and Schulz, J.C., 1977, Magnus effect in saltation: Journal of Fluid Mechanics, v. 81, p. 497-512.
White, B.R., Leach, R.N., Greeley, R., and Iversen, J.D., 1987, Saltation threshold experiments conducted under reduced gravity conditions: AIAA, 25th Aerospace Sciences Meeting, 12-15 January, Reno, Nevada, Paper AIAA-87-0621, 9 p.
Willetts, B.B., 1998, Aeolian and fluvial transport: Royal Society (London), Philosophical Transactions, Series A, v. 356, p. 2497-2513.
Willetts, B.B., and Rice, M.A., 1985, Intersaltation collisions, in Barndorff-Nielsen, O.E., ed., Proceedings of the International Workshop on the Physics of Blown Sand: Demark, University of Aarhus, Department of Theoretical Statistics, Memoir 8, p. 83-100.
Williams, G., 1964, Some aspects of the eolian saltation load: Sedimentology, v. 3, p. 257-287.
Zingg, A.W., 1952, A study of the characteristics of sand movement by wind: M.S. thesis, Kansas State College, 79 p.
Zingg, A.W., 1953, Wind tunnel studies of the movement of sedimentary material: State University of Iowa, Iowa Institute of Hydraulic Research, Fifth Hydraulics Conference, Proceedings, McNown, J.S., and Boyer, M.C., eds., p. 111-136.


