9.6: The Effect of Density Ratio
- Page ID
- 4209
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)It was mentioned in Paragraph 27 above that the density ratio \(\rho_{s}/\rho\) might be important in governing the motion threshold. In that case, the dimensional analysis put forth in the earlier section should be extended in order to include the effect of relative density:
\[\text{threshold} =f\left(\rho, \rho_{s}, \mu, \gamma^{\prime}, D, \tau_{\text{o}}\right) \label{9.9} \]
and, nondimensionalizing in the same way as before,
\[\frac{\tau_{c}}{\gamma^{\prime} D}=f\left(\frac{\rho u_{*} D}{\mu}, \frac{\rho_{s}}{\rho}\right) \label{9.10} \]
where \(\tau_{c}\) is the threshold value of the bed shear stress.
To my knowledge, little consideration has been given to that possibility in the literature on threshold. Shields himself plotted data not just for quartz-density sand in water but for amber (specific gravity \(1.06\)), lignite (specific gravity \(1.27\)), and barite (specific gravity \(4.25\)). The points for amber and lignite lie slightly above the curve, and the points for barite lie slightly below the curve, suggesting that \(\rho_{s}/\rho\) has at least a slight effect. A later study by Ward (1969) showed the same results, although with greater range of difference in threshold with density ratio. I am not aware of any more recent studies of the effect of density ratio on thresholds in water flows. A potential pitfall in interpreting these results, however, is that the experiments were not controlled for possible effects of particle shape, and in the case of plastic beads (styrene, specific gravity \(1.18\); polyethylene, specific gravity \(1.06\)) in oil, the possibility of subtle particle- to-particle forces were not considered.
The results seem counterintuitive, at least to this observer: should it not be the case that the particles with greater density, and thus greater inertia, would be less likely to be set into motion by suddenly greater fluid force on the particle than a particle with lesser density? A specific set of experiments in which a criterion for threshold is applied uniformly, and in which particle sorting and shape are adjusted to be the same for the various sediment batches with different density, might bring some clarity to the issue.
If the decrease in Shields parameter (the dimensionless threshold shear stress) with increasing density ratio is indeed real, then it should be even greater for the case of quartz particles under the wind, for which the density ratio is far greater than for even the densest solid particles under water flows. Extensive observations of the threshold bed shear stresses for several particle compositions, sizes, and densities under wind (Iversen et al., 1976) gave results of about \(0.1\) for the threshold Shields parameter over a range of boundary Reynolds numbers from about \(5\) to about \(50\), and their results were generally consistent with earlier wind-tunnel studies of threshold (see Chapter 11 for more on eolian thresholds). Thresholds under water flows in this range of \(\text{Re}_{*}\) average around \(0.6\), judging from the modified Shields plots presented by Buffington et al. (1997) (see Figure 9.5.1 above). The increase in dimensionless threshold with increasing density ratio does therefore seem to be real.
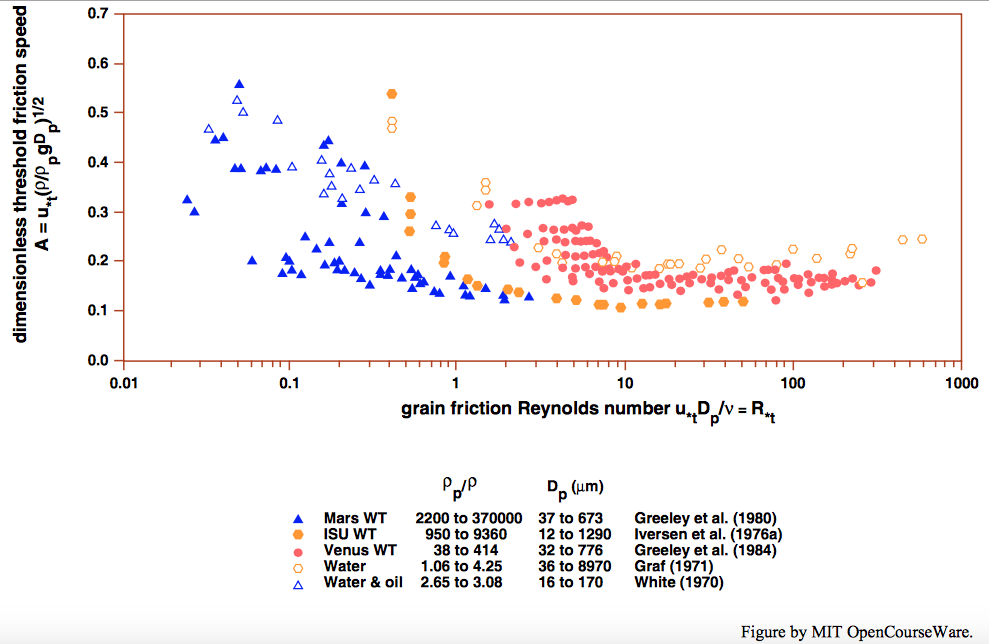
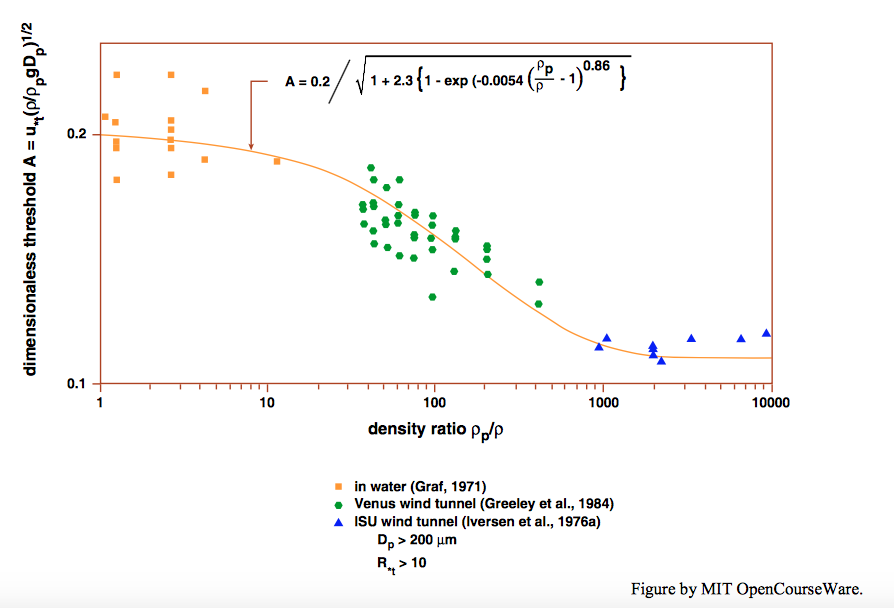
In a later study by Iversen et al. (1987), in which they synthesized earlier results on threshold over a wide range of density ratios, they purport to show that the dimensionless threshold decreases systematically with increasing density ratio from that characteristic of mineral particles in water to that of mineral particles in the extremely low atmospheric density of Mars; see Figures \(\PageIndex{1}\) and \(\PageIndex{2}\). Be on your guard here, however: their dimensionless coefficient A uses \(\rho_{s}\) instead of \(\left(\rho_{s}-\rho\right)\) in the variable \(\left(\rho_{s}-\rho\right)g\), called \(\gamma^{\prime}\) in these notes, in the denominator, so the results for the threshold in water, shown on the left-hand side of Figure \(\PageIndex{1}\), cannot be compared directly with the conventional Shields curve. The decrease in their threshold coefficient \(A\) from the Venus-wind-tunnel case to the Mars-wind-tunnel case seems to support their position, but even so the values for the Venus wind tunnel, for which the density ratio is not greatly different from that of sand in water, is significantly higher than the generally accepted values shown on the Shields diagram and its later modifications, discussed above. the matter seems (at least to this writer) not be settled.
References Cited Chapter 9
Buffington, J.M., and Montgomery, D.R., 1997, A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers: Water Resources Research, v. 33, p. 1993-2029.
Chepil, W.S., 1958, The use of evenly spaced hemispheres to evaluate aerodynamic forces on a soil surface: American Geophysical Union, Transactions, v. 39, p. 397- 404.
Chepil, W.S., 1961, The use of spheres to measure lift and drag on wind-eroded soil grains: Soil Science Society of America, Proceedings, v. 25, p. 343-345.
Coleman, N.L.,1967, A theoretical and experimental study of drag and lift forces acting on a sphere resting on a hypothetical stream bed: International Association for Hydraulic Research, 12th Congress, proceedings, v. 3, p. 185-192.
Coleman, N.L., and Ellis, W.M., 1976, Model study of the drag coefficient of a streambed particle: Third Federal Interagency Sedimentation Conference, Denver, Colorado, Proceedings, p. 4-12.
Einstein, H.A., and El-Samni, E.A., 1949, Hydrodynamic forces on a rough wall: reviews of Modern Physics, v. 21, p. 520-524.
Grass, A.J., 1970, Initial instability of fine bed sand: American Society of Civil Engineers, Proceedings, Journal of the Hydraulics Division, v. 96, p. 619- 632.
Hjulstrøm, F., 1939, Transportation of debris by moving water, in Trask, P.D., ed., Recent Marine Sediments; A Symposium: Tulsa, Oklahoma, American Association of Petroleum Geologists, p. 5-31.
Iversen, J.D., Pollack, J.B., Greeley, R., and White, B.R., 1976, Saltation threshold on Mars: the effect of interparticle force, surface roughness, and low atmospheric density: Icarus, v. 29, p. 381-393.
Iversen, J.D., Greeley, R., Marshall, J.R., and Pollack, J.B., 1987, Aeolian saltation threshold: the effect of density ratio: Sedimentology, v. 34, p. 699-706.
Lavelle, J.W., and Mofjeld, H.O., 1987, Do critical stresses for incipient motion and erosion really exist?: Journal of Hydraulic Engineering, v. 113, p. 370- 385.
Miller, M.C., McCave, I.N., and Komar, P.D., 1977, Threshold of sediment motion under uinidirectional currents: Sedimentology, v. 24, p. 507-527.
Neill, C.R., 1968, Note on initial movement of coarse uniform bed-material: Journal of Hydraulic Research, v. 6, p. 173-176.
Shields, A., 1936, Anwendung der Ähnlichkeitsmechanik auf die Geschiebebewegung: Berlin, Preussische Versuchanstalt für Wasserbau und Schiffbau, Mitteilungen, no. 26, 25 p.
Sundborg, A., 1956, The River Klarålven: Chapter 2. The morphological activity of flowing water—erosion of the stream bed: Geografiska Annaler, v. 38, p. 165-221.
Vanoni, V.A., ed., 1975, Sedimentation Engineering: American Society of Civil Engineers, Manuals and Reports on Engineering Practice, No. 54, 745 p.
Ward, B.D., 1969, relative density effects on incipient bed movement: Water Resources research, v. 5, p. 1090-1096.
Yalin, M.S., 1977, Mechanics of Sediment Transport, 2nd Edition: Oxford, U.K., Pergamon, 298 p.


